鸣 谢

非常感谢给予作者帮助的下列人员，他们都是声誉卓著的研究者与畅销书作家：

莫里斯•K.吉塞普（Morris K.Jessup）、卡尔•艾伦（Carl Allen）、杰克•帕森斯（Jack Parsons）、伊凡•T.桑德森（Ivan T.Sanderson）、威廉•L.摩尔（William L.Moore）、查尔斯•伯利兹（Charles Berlitz）、J.马森•瓦伦丁（J.Manson Valentine）、阿尔弗雷德•别里克（Alfred Bielek）、普勒斯顿•尼克尔斯（Preston Nichols）、彼得•穆恩（Peter Moon）、亚瑟•T.温弗里（Arthur T.Winfree）、约翰•格里本（John Gribbon）、艾略特•R.布朗（Eliot R.Brown）、保罗•J.那金（Paul J.Nahin）、威廉•克里斯（William Corliss）、杰罗姆•克拉克（Jerome Clark）、布拉德•斯坦格（Brad Steiger）、提摩西•贝克利（Timothy Beckley）、迈尔克•塔尔伯特（Michael Talbot），边缘地带科学协会（Borderland Sciences）的莱利•克雷布（Riley Crabb）以及其他诸位。

你们的辛勤劳动将会流芳百世！

第一章

时间旅行的基础：来自量子力学和超弦理论

时间旅行是潜在的人在潜在的空间里进行的。

我会告诉你谁能让时间在此刻缓慢前行；

谁能让时间在此刻稍微加速；

谁能让时间在此刻飞速前进；

而谁又能让时间在此刻停止。

——威廉•莎士比亚（William Shakespeare）

人都会有一种超自然意识，使其超越空间与时间的正常边界——需要说明的是，有一个超越了物质世界的维度存在。

——埃德加•米歇尔（Edgar Mitchell），

阿波罗14号宇航员

时间和重力的历史理论

欢迎来到101时间旅行。数千年来，我们多次尝试去解释或者描述万有引力以及一种“时间”现象。在古代哲学文章里，这种现象有时被称作“时间之箭”。为了获得对时间旅行的充分了解，我们需要理解时间、地心引力以及“统一场”的历史理论。

我们对于我们周遭的各种物理力量仍然还不能全然理解。但随着时间的推移，我们能更好地理解存在于我们周围的神奇宇宙以及它运作的方式、时空之间的相互影响以及无处不在的所谓的量子场。发现超时空裂洞以及其它时空隧道是理解宇宙如何运作及其神奇本质的必然结果。

虽然西方社会经历了许多黑暗时代，但是早在公元前330年，亚里士多德（Aristotle）所谓的四元素——土壤、水、空气和火，自然界中都有其独特的地位。他认为，地球上的物质尽管本质相同，但是重量较大的物质下落的速度较快，能够比其它物质更快落到地上。

伽利略•加利雷（Galileo Galilei，1564-1642）在1604年推断重力产生了一种明确的加速度，而不是速度，并且这种加速度对于真空中运动的物体的影响是相同的。重力加速度的普遍性正是基于众所周知的弱等效原理。

当艾萨克•牛顿（Isaac Newton，1643-1727）先生于1606年意识到月球轨道的运行如同苹果掉落到地上一样都依赖于地心引力时，他为地心引力理论做出了重大的贡献。在引力公式中，引力与其到地心距离的平方成反比。牛顿将平方反比定律与他的三大运动定律、物体之间的引力以及它们之间距离的平方的反比结合在一起，形成了重力普遍理论。此理论阐述了在每个物体之间都存在吸引力，其大小与它们之间距离的平方成反比。

勒奈•笛卡尔（Rene Descartes，1596-1650）在较早的时候根据行星上的内部压力漩涡提出了非定量的引力理论，但是牛顿并没有提供引力产生的原因。实际上，他甚至拒绝将它称为一种引力，而是将它称为“机体相互之间产生的重力吸引”。这一理论足以推出开普勒（Kepler）的行星运动理论、海洋潮汐以及分点岁差规律。在1846年，人们利用这一理论推测并发现了一个新的星球——海王星。因此，牛顿的万有引力定律被认为是人类科学史上最伟大的突破之一。

如果用数学的方式来表现牛顿的万有引力定律，那么万有引力是F，它的公式为F=Gm(1)m(2)/r^2，其中两个粒子的质量分别为m(1)和m(2)，粒子之间的距离为r。G是万有引力比例常数，它是一个不能够用太阳系观察数据来确定的未知量，它能够提供质量的比例以及G和质量之间的乘积。G的值最初是由亨利•卡文迪什（Henry Cavendish）在1798年确定的，他计算出了两个已知重量的球体之间的万有引力的大小。这个实验后来被称为“测量地球的重量”，因为一旦G的值确定了，那么地球的重量m(e1)，就能够根据天文学上的Gm(e)价值公式来得到确认。这个实验已经在多次重复的基础上有了很大的提升。目前学术界公认的G的值为6.67259×10^(-11)N•m^2/kg^2。

现代理论

1905年，阿尔伯特•爱因斯坦（Albert Einstein）提出了相对论，这个理论很好地修正了牛顿的万有引力定律。爱因斯坦试图以一种与观察者的移动相独立并与所选择的坐标相协调的方式来描述引力。他的工作促使了几何理论的产生，这种理论通过纯粹的时空连续体来描述地心引力。根据这一几何理论，地心引力影响着一切在空间中运动着的所有形式的物质和能量。因此，爱因斯坦的理论服从弱等价原理，所有做自由落体运动的物体的重力加速度相同。

除了描述了地心引力对物体的影响，爱因斯坦还描述了物体对于地心引力的影响。爱因斯坦在1915年完成的这个理论被称为广义相对论。尽管爱因斯坦的理论与牛顿的理论有着很大的不同，但是它们在系统（这个系统的引力场十分微弱，其速度与光速比较起来也很慢）预测上基本有着相同的效果。行星运动促使了经典牛顿理论的产生。但爱因斯坦的理论解释了一些牛顿从未意识到的存在于太阳系中的现象。

比如水星近日点进动。19世纪，根据牛顿理论的预测，人们认为它会以每世纪43″的速度进动；爱因斯坦理论所预测的结果与其在岁差上有着很大的不同。另一个类似的自然现象是太阳引力场中光线的弯曲度，牛顿的理论根本没有预测到这一现象的出现。爱因斯坦关于日全食的预测在1919年得到了亚瑟•S.爱丁顿（Arthur S.Eddington）的证实，随后由其他人将准确率提高了1%。爱因斯坦也同样预测了引力红移效应，它是强大的引力场中所发出的电磁波频率的变化现象，这个预测最终在1960年由罗伯特•庞德（Robert Pound）和格伦•雷布卡（Glen Rebka）进行了验证。在引力红移效应得到证实之后，1964年，欧文•夏皮罗（Irving Shapiro）在这个理论的基础上，利用广义相对论预测了经过太阳附近的信号的延迟。

此外，爱因斯坦的广义相对论同样定性预测了其它几个体系中的新现象，它在研究宇宙学方面显得尤为有用。根据相对论学说，宇宙要么是无限扩张要么就是无限紧缩的。但爱因斯坦还不能够完全确定这种预测，为了顾及到一个静态的宇宙，他修改了他的方程式。然而在1929年，埃德温•哈勃（Edwin Hubble）发现宇宙是在无限膨胀的。重力最终是否会导致宇宙体系的崩溃是当前学术界研究和辩论的热门话题。广义相对论还预测了物质质量在非匀速运动中所产生的引力波，但是这种波太过微弱了，以至于科学家们还没能明确地侦测到它。最后，爱因斯坦的相对论还预测了足够大的坍塌引力会导致物质陷入宇宙黑洞之中。现在，越来越多的科学证据表明，一些天文系统中可能有黑洞的存在。

爱因斯坦的广义相对论并不是20世纪产生的唯一引力理论，但是它也许是最简洁最讲究的理论。所有可行的引力理论都必须像爱因斯坦的理论那样完整、自持并且有相对论的特质。它们还必须能解释牛顿理论的局限性，坚持弱等价原则，并能够在同一位置在理想时间内测试出相同的爱因斯坦位移，以上三点被认为是最基本的要求。实验表明达到以上的条件是最基本的要求，并且L.I.席夫（L.I.Schiff）推测它们可以通过几何原理、度量和理论来进行验证。

最有资格与之相提并论的应该是布兰斯•迪克（Brans-Dicke）理论。就像广义相对论那样，它是一个满足了基本标准的几何理论。它的电磁场方程式不同，然而，该理论认为时空几何不仅受到物质本身的限制，而且受到另外的标量场的影响。与爱因斯坦的计算不同，布兰斯•迪克理论并不能预测水星的近日点位移。

一些近期的理论试图以非几何的方式解释万有引力定律，它们试图用一种被称为引力子的微粒来解释万有引力。这些所谓的超对称理论将引力现象归于量子物理学的领域之中。它们试图证明四种相互作用的基本性质是彼此关联的，它们对于宇宙的诞生来说是一种独立但又统一的力量。

多维分析学说还提出了关于不变的万有引力常量G的相关问题。这个问题最早是由英国物理学家保罗•狄拉克（Paul Dirac）在他那所谓的“大量”假说中提出的。狄拉克注意到在原子条件下电磁力的放射性和强度以及地心引力（大约是10^40）的放射性和强度在大体上跟宇宙的年龄相关。他猜测，在如此相似的情况下是否掩藏着深刻的物理联系，并提出G的值是否有可能随着宇宙年龄的不断增加而逐渐减小。如果G的值在减小，那么引力时间会随着原子时间的改变而改变。但是到目前为止，还没有任何实验可以证明这一切是真实存在的。

统一场理论

在理论物理学中，统一场论也许最广泛的定义是一种方程式原理，这种原理统一了地心引力、电磁、弱核力和强核力四种相互作用的基本性质。而且，还没有能囊括一切的理论存在。

历史上，阿尔伯特•爱因斯坦是第一个尝试用一系列统一场论来统一地心引力和电磁学这两种基本因素的。也就是说，他在完成了对自己的地心引力理论（及广义的相对论）的陈述后，开始用詹姆斯•克拉克•麦克维斯（James Clerk Maxwell）给出的著名电子方程式来论证他的结果。爱因斯坦的想法是从本质的几何学观点上，把他自己的和麦克维斯的描述联系起来。但是他最终失败了。然而，这次失败主要原因还是在那个时代强核力和弱核力还没有被发现。

另外的一些尝试是由德国物理学家赫尔曼•威尔（Hermann Weyl）和美国物理学家约翰•惠勒（John Wheeler）提出的，把电磁理论整合到普遍相对的几何形式中。尽管其中一些理论只是看上去很完美，但实际都缺乏跟量子现象的联系，这种现象对于相互作用而非地心引力非常重要。

随后的一些整合尝试是从一个完全不同的角度开始的，整合的量子场理论用来描述，或者可以说描述了四个基本原理的相互作用。目前为止最成功的就是由谢尔顿•格拉肖（Sheldon Glashow）、史蒂文•温伯格（Steven Weinberg）和阿卜杜勒•萨拉姆（Abdus Salam）共同提出的弱电理论。这个理论结合了电磁场理论和弱相互作用理论。这个理论简化来说就是，力是由四种不同的无质量的玻色子相互作用而传播的。通过一种“破坏的对称性”，这三个玻色子，W(+)、W(-)和Z（0）就产生了质量，质量以质子的50到100倍增加，第四个玻色子，也就是光子，仍然是无质量的。1983年，W和Z玻色子在欧洲核子研究委员会(CERN)实验室的高能物理实验中被发现。因此，温伯格、萨拉姆和格拉肖获得了1979年的诺贝尔物理学奖。

除弱电理论之外，也有一些其他的整合理论被提出来。其中一些涉及强相互作用，而一些“万能理论”也试图包括万有引力。后者也被称为超对称理论。然而，目前为止，这些都还未取得突破性进展。

量子力学

根据爱因斯坦的广义相对论，任何事物，无论在光速或者更快的速度中都不能进行时间旅行。然而，量子力学有一种现象叫隧道现象，在理论上能够提供一种原理让物体在比光速更快的速度中从一个地方移动到另一个地方。威廉•克里斯1995年提到，德国研究者声称在4.7光速下传送了莫扎特(Mozart)的第40交响曲第5节。

量子力学是一种基础理论，在20世纪被物理学家用来描述原子和亚原子现象。它还成功地广泛运用于观察一系列宇宙图片。

虽然量子力学借鉴了牛顿力学的一些观念，即早先的物理现象，然而与牛顿力学本质上是不同的。比如，在牛顿物理学中，数量是被认为持续可变的，在一定范围内可取任何值。另一例子是角动力，即粒子被一中心吸引沿圆形轨道旋转，它与速度乘以中心距粒子的距离值成正比。因为牛顿力学中距离可以取任何值，所以角动力也是如此。另一方面，在量子力学中，角动力常常被规定成某些离散值，这些离散值的比率是简单的有理数。

量子力学和早先的物理理论更本质的区别在于用一种可能性，即用一种基本思维来解释量子力学如何来诠释这个世界。这就很明显是在用量子力学和牛顿力学来预测未来。牛顿力学中描述的一些事物，如太阳系，如果能一次性精确测量出，那么对于太阳系未来动向的精确预测是有可能的。在量子力学的描述中，甚至对一个简单的单电子原子都能精确预测出其诸多行为的可能性。对不稳定的放射性核的描述就能说明这一点。当单个的核子衰变时，量子力学就不能进行预测，尽管如此，如果搜集了许多相同的原子核，那么能指出何时这个核子会衰变。这个量子力学的新现象被一些知名物理学家，如艾伯特•爱因斯坦所抵制。不管怎样，它的出现成为原子与亚原子水平上不可忽视的一个特征。

早期发展：普朗克的成果

历经30多年的时间，量子力学蓬勃发展，期间成功地解释了多个物理现象。第一个量子理论用来分析电磁辐射是如何产生的。1900年，马克思•普朗克(Max Planck)做到了。普朗克尝试研究在不同的频率下，热的物体辐射的分布，比如太远的表面。根据观察结果他得出结论，辐射不是持续发出的，就像早先认为的一样。相反，辐射是以一种被他称为量子的离散量发出的。对于这些量子、频率f和能量释放量E之间往往存在一种关系，即E=hf。这里的h就是被普朗克引入的普适常数，现在以他的名字命名。普朗克常数以时间乘以能源为单位，其数值接近6.63×10^（-34）焦耳秒。普朗克分析结果的独特之处在于，这个公式能够表达出任何频率下的物体的辐射量。这个联系，即黑体分布，和实验结果相一致。

在普朗克的理论中，量子的性质是十分神秘的。这个谜于1905年被爱因斯坦解开，他提出光本身就是一个由单个套件组合的能源，后来被称为光子。爱因斯坦还提到光的频率与光子合成的能量有关，这是根据普朗克公式得出的。爱因斯坦的光量子概化理论被许多与他同时代的科学家所排斥，其中包括普朗克。而后，被罗伯特•密立根（Robert Millikan）的光电效应实验证实，并且阿瑟•康普顿（Arthur Compton）从康普顿现象中发现了这一理论，并且用电来进行光子散热。

另一个具有代表性的早期量子运用的想法是尼尔斯•波尔（Niels Bohr）提出来的，1913年他提出一个假设，氢原子的电子角动力只能有一个值，这个值即普朗克常数的整数倍除以2π，那么它可以派生出由原子发出的光的频率。波尔理论暗示了只有特定的能量值，电子才可能存在于原子中，即如果有一个最小值，那么在这种最小值的状态下，电子是无法放射能量的。这个结果帮我们解释了原子如何能够保持稳定，也说明了一个元素的所有原子如何有一样的化学性质。然后，他证明了波尔理论对于原子的拓展要比氢气复杂得多。而且，牛顿定理和量子理论的奇怪组合让物理学家很难取舍，到底该遵循哪一个物理原理。

量子力学形式

实际的量子力学的发展，即数学的理论，于1924年到1927年才开始。起初，有两种看起来不相同的途径：一是维尔纳•海森堡（Werner Heisenberg）发现的矩阵力学和欧文•薛定谔（Erwin Schrodinger）发现的波动力学。然而，事实表明这是一个单独理论的两个不同方面，后来被称为量子力学。这个没有被定义的现象是被保罗•狄拉克（Paul Dirac）发现的。在矩阵力学中，物理量如粒子的位置，不是用数字表示，而是用数学量来表示，如矩阵。矩阵力学对于处理相应能量水平的小数的情况有用，如在磁场中的定角动力。

波动力学对于能量水平的数目无限大的情况更有用，如原子中的电子。这个是建立在路易斯•德布洛意（Louis deBroglie）的早期理论之上的，即粒子如电子与它们的联系成波状。波的波段（h）、伽玛（γ）与质量（m）和速度（v）有联系，粒子与伽玛的联系是γ=h/mv。这可以推断出电子以十分之一光速移动，如电视显像管产生的那些，波长大约10^（-10）米，或者约为在透明固体中原子之间的距离。德布洛意的预测被克林顿•戴维斯森（Clinton Davisson）和乔治•汤姆斯（George Thomson）证实。他们让电子波穿过了金属球，随即产生了衍射图案，跟X射线产生的一样。

1925年，欧文•薛定谔发展了方程式，现在以他的名字命名。这个方程式描述了电子如何与波动联系起来或者其他亚原子粒子在各种不同作用力的影响在空间和时间中的运动情况。这个方程式有多种解答方式，而且薛定谔强调对于一个粒子系统，其解答结果必须满足任何位置。当遇到电子在氢原子中的情况时，薛定谔方程式能马上给出准确的能量值，像以前波尔算出的一样，这个方程式能适应更复杂的原子，甚至完全没有被原子束缚的粒子。在很多例子中发现薛定谔方程式能给出粒子行动的准确描述，也证实了粒子没有在接近光的速度下运动。

抛开这些不谈，波动理论并不够完善。尽管这个公式成功了，但是波动的意义还是不清楚。薛定谔认为在空间内波动的强度的一个点上，代表了电子在那个点上的总量。那么，只要释放了电子，就无法集中在一点了。然而，这个理论很快被发现是不成立的，因为，如果一个粒子最开始集中在一点，大多数例子表明粒子会迅速传递到递增的更大区域，这就与观察到的粒子的行为相矛盾。

对波动正确的解释是由马克思•伯恩（Max Born）提出的。当他在研究如何用量子力学来描述粒子间的碰撞时，意识到德布洛意-薛定谔波动有一种测量的可能性，找到空间中粒子两点之间的距离。换句话说，即度量衡常常聚焦的是一整个粒子，而不是其中一部分。但是在一些强度小的区域，粒子不常被发现，然而在强度大的区域，粒子经常被发现。

海森堡的不确定原理

1927年，海森堡对量子力学的进步做出了重要的贡献。他分析了很多“思维实验”，这些实验是为了提供一些关于粒子位置和速率而设计的。这需要显微镜来呈现电子的图像。众所周知，因为光的波动性质，一个精确的电子图像需要波段长而且频率高的光。然而，普朗克-爱因斯坦关系暗示了这样的光需要光子有巨大的能量和动力。在这样的光子和电子间的碰撞，电子动量会从碰撞时开始不受控制地变化。结果是，随着电子理论的普及，精确度的增长是不可避免的，但是在其动量领域则是精确度的损失。在这个理论和相关分析的基础上，海森堡建立了他的不确定准则，这个准则以它最简单的形式表达了未知Δx和未知Δp之间的相互关系，Δx是物体的位置，Δp是我们所知道的它的能量。根据（Δx）（Δp）给出的不确定关系，其结果小于h/4π。对于物体每天的大小，相较于普通实验的不确定性来说，同时测量的限制就无足轻重了。因为这个原因，对于那些物体来说，牛顿定理和量子力学之间几乎没有显著的区别。然而，对于一个原子中的电子，它的不确定性限制是十分明显的，以至于他们能基本确定其大小和原子能量的最小值。

根据伯恩的波动强度的可能性描述和海森堡的测不准原则，量子力学的标准元素非决定性阐释早在1930以前就已经形成了。通常被人知晓的是哥本哈根阐释，因为尼尔斯•波尔（Neils Bohr），这位使现象公式化的伟人，那段时期，在哥本哈根建立了非常有影响力的物理机构。然后，许多科学家对哥本哈根阐释表示不满并加以批判，其中包括爱因斯坦和薛定谔，他们接受的只是量子力学的数学公式。正确阐释数学公式被认为是一个普遍难题。

发现定理以后，接着就开始用量子力学解释了很多原子物理学和化学领域的问题，如许多电子原子的结构和分子的结构。根据以前的观察和预测，这些应用大部分是成功的。后期成功预测的例子是，依靠相对定向的核角动力，氢分子可以以两种形态存在。1928年，由于这些成功的例子，保罗•狄拉克称量子力学是“涵盖一切化学及大部分物理学”的领域。虽然，陈述的第二半部分还没有得到证实，但是量子力学的延伸成功解释了许多物理现象。比如，19世纪30年代和40年代，乔治•伽莫夫（George Gamow）运用量子力学解释了放射性原子核的α衰变。

为了一些原子核的应用和原子物理学计算的准确性，延伸量子力学的原始公式，使其与爱因斯坦的特殊相对论保持一致，已经变得越来越重要了。1927年，狄拉克是第一个着手实施的人，并以他的名字作为方程式名。狄拉克方程很快成功证实了其在计算电子的性质方面的巨大作用，如自旋。自旋是轴通过电子角动力自转的，有点像地球围绕着自己的轴转动。早先我们知道的是，所有电子的自旋都是h/4π，但是原因并不清楚。狄拉克方程解释了这个原因，并且正确推算出一些自旋电子的磁力，并且做出了一个新的预测，在有相反电荷的情况下，有一种自旋的粒子存在。后来被称为正电子的这些粒子，是1932年被卡尔•安德森（Carl Anderson）发现的。它们是第一个反粒子案例，它们的存在被许多理论预测到了，量子力学和特殊相对论都能对其进行解释。

量子场论

对反粒子的研究，了解它们的性质，展示出相对量子理论的新方面，即事物的产生和消亡。狄拉克预测到并且很快观察到，当高能量的光子穿过物体时，电子和正电荷可以成对一起产生。并且，一个正电荷靠近一个电子后，两者会同时迅速消失，随即转化为几个光子。为了阐述粒子变化的数量上的转化，应用量子力学新理论，即场论是非常必要的。

在牛顿物理学中，一个领域代表了一个物理数量，如电场力，根据精确的数学方程式，电场力在时间和空间里从一个点到另一个点变化。这种经典领域可以在不同的点上有不同的数值。普通的量子理论最先被狄拉克运用到电磁领域。这种自动结合暗示了普朗克和爱因斯坦提出的有属性的粒子存在。而且，他能运用量子场论的形式来描述光子如何被带电粒子放射和吸收，如原子中的电子辐射，后来被称为QED，或者量子电动力学。19世纪50年代后期，QED一个重要的实际应用是激光。

许多物理学家都认为，早先的未知领域都涉及各种类型的粒子变化的过程。比如，1933年，恩里科•费米（Enrico Fermi）利用量子场论解释了电子从核子的发射，这个过程后来被称作β衰变。从普遍的经验中能得出，量子场论能够适应量子力学的规律，而且符合相对论，自然解释粒子的产生和消亡的过程。

量子场论也有一些不可预见的后果。比如海森堡的测不准原则在某段时期内并不能严格遵守能量守恒定律。因此，像电子一样的其他粒子能稍微发射然后重新吸收其他的粒子，比如光子。这种瞬变被称作虚粒子，它影响了我们衡量电子的性质。需要强调的是，如果不存在虚粒子，它们的质量会发生改变。基于虚粒子而多余的质量叫本身质量。不幸的是，19世纪30年代，物理学家尝试计算出基于虚粒子的本身质量，然而他们得到了一个无限值。一段时间里，这个结果使得研究量子场论的进程瘫痪。然而，19世纪40年代，他们找到了一种方法来处理本身质量的无限值。这种方法叫重整化，从那时候开始它便支撑了整个量子场理论。

重整化

重整化显示，本身质量是不能被直接测量的。只有结合了本身质量和固有质量才有可能观察到电子。亨德里克•克拉默斯（Hendrik Kramers）是第一个提出把本身质量的无限值与一个固有质量的无限值结合，然后得出一个有限可观察的质量。接着，它可能表达出所有在此方面与其他观察到的数量总和，防止无穷值的问题出现。这个步骤就被称作质量重整化，是十分微妙的计算。事实上，19世纪40年代末，因为新的技术引入，这种理论才被朱利安•施温格（Julian Schwinger）和理查德•费曼（Richard Feynman）完善。这种理论在各个阶段都与相对论保持一致，而不像以前的理论，把时间和空间进行了严格的区分。费曼理论包括一些暗示图片的运用，现在被称为费曼图表，它与计算过程中的所有步骤都相关。比如，电子产生光子，被画成一根没有额定长度的固体线，一段波浪线形代表了电子，开始于电子线路中间的直线代表光子。费曼描述了一组规律，即能根据相关的图表直接算出任何时候突发情况的概率。

19世纪40年代末，为了研究氢原子的电子能量和磁性，基于虚光子的放射和吸收，科学家运用费曼定律和薛定谔定律计算出了小修正。那些计算拥有更高的准确度，并且在某些案例的观察中，其精确度达到了令人不可思议的亿分之一。这可能是目前物理科学取得的最大的成功。

量子电动力学成功之处在于，让许多物理学家认为，可以用其他重整化量子场论描述那些不符合量子电动力学的亚原子粒子的性质，如中子和质子结合成原子核的强大力量，以及核衰变的弱力。因为对重整化理论和适应这种理论的粒子了解不够，所以这样的愿望许多年来没有实现。19世纪60年代到70年代，这种状况得到了改观，因为杨振林（Chen-Ning Yang）和罗伯特•米尔斯（Robert Mills）发现了一种特别的重整化量子场论，被称为规范场论。规范场论其中一种类型叫量子色动力学，或者叫QCD，它是一个描述夸克之间强相互作用的标准动力学理论，而不是针对质子和中子的。夸克是由假想的原子和中子组成的，受到其他粒子强力相互作用的影响。第二规范场论是由谢尔顿•格拉肖、史蒂文•温伯格和阿卜杜勒•萨拉姆提出的，用来描述电磁和弱相互作用，从而统一了一个单一理论性质的两个重要方面。

尽管重整化量子场论成功了，但是有些杰出的理论物理学家，如狄拉克对此表达了疑虑。尽管这些理论得到的数值是有限的，但是它是通过无限数量的评估得到的，这些量包括数学上的怀疑和美学上的审定。

量子力学的解释：隐变量理论

量子理论已经有60年的历史，为许多物理现象提供了正确的解释。但是，有些物理学家对于理论本身和当时的哥本哈根理论还心存疑虑。这些批评大多数来自于早先量子力学理论的代表。

批评之一就是它的不稳定性。尽管稍后对其他方面进行了拓展，但是这是爱因斯坦一开始就留下的缺陷。因为，一些个别的放射性核在特定的时间会衰变，所以爱因斯坦和其他物理学家认为一个完整的物理理论应该能准确预测时间，而不是根据数据统计去判断。爱因斯坦并没有对他所提出的那些理论进行分类，来代替量子理论，而其他物理学家建议在所谓的“隐变量”理论里找到一种解决方法。在隐变量理论中，我们可以测量有关事件的物理性质，而量子力学只能大概预测。数学家约翰•冯•诺依曼（John Von Neumann）很早就提出，隐变量理论不能够完全和量子理论的预测符合。这个说法还没有被证实，然而，有可能隐变量理论能和所有已经观察到的结果进行公式化的对比。但却没有一个物理学家找到合适的方法。

量子理论所作出的解释的第二个问题是关于测量方法的，这让很多接受它的人感到困惑。薛定谔波动方程能用于描述任何系统从一刻到另一刻的变化。如果在一个时间点上，能知道空间内任何位置的波动，那么稍后就能预测其他任何地方的变化。然而，知道了波动的强度，顶多只能预测其度量衡。当度量衡确定时，观察者能够立即获得至少一个关于这个系统性质的准确信息，如它的能量。这种把预测转化为准确信息的现象称为减少的波函数。这就可以证明，即使把测量仪和被观察的系统考虑进去，还是不能用薛定谔方程来描述这种减少。许多科学家对这个结果持有不同的态度。持赞成观点的人认为观察者的主观性在波动的减少作用中起了基础作用。反对者认为，因为量子力学不能囊括这种减少现象，所以它是不完整的。也许最为广泛接受的观点是，减少的波函数往往是包涵在微观的物体中，如电子，用测量仪来测量微观的系统。当这种互动发生时，测量仪肯定会发生改变，而这种改变使电子的波函数减少。也许这个观点有一些是正确的，但是它只能解决一部分问题，因为它自身的不可逆转性还没有完全被了解。

爱因斯坦-波多尔斯基-罗森悖论和贝尔定理

另一个关于量子理论的解释来自于爱因斯坦与鲍里斯•波多尔斯基（Bois Podolsky）以及弥敦道•罗森（Nathan Rosen）的共同研究。1935年他们发表了一篇文章指出，对于量子力学的预测，在某些特定地方是不确定的，有些例子中，他们想的与实际的合理标准是冲突的。这种状况被设想成，在原始的物理系统中有一个整体，然后分割成两部分，最终两部分会远远分开。有一个现实的强加条件，当测量分开的系统的其中一部分时，另一部分不能进行干扰。他们分析的一个例子是，一个包含了电子和质子的原子，每个原子有h/4π的自旋角动量，但是整个自旋却为0，因为原子分裂后，电子向一个方向运动，而质子朝另一个方向。因为保留的角动力，电子和质子整个角动力被认为是零，即使它们隔得很远。如果一个物理学家能够确定电子自旋沿着某一方向运动，那么他可以立即推断出质子沿相反的方向自旋。这个现实条件表明，在测量出电子前，质子自旋已经可以确定一个值。

1964年，约翰•贝尔给出了一个不同的意见，与爱因斯坦的理论相矛盾的重力力学。他的发现来自于大量电子和原子的统计测量数据，被称为贝尔定理。这个定理表明，任何原理都能满足爱因斯坦的现实条件，这个现象是一个局部情况，即粒子被确定了性质后，那么就一定以为这一系列测量结果之间存在关系。针对爱因斯坦实际条件和贝尔定理的一系列测试实验已经结束。结果是反对爱因斯坦的实际条件，支持量子力学。

研究和运用量子力学被认为是现代物理学的一个核心。这种研究的一方面其实是在非常复杂的境况下，即不能做出正确的决策时，找到一种近似的理论来适应量子力学的基本准则。许多凝聚态物理中的研究都能用到这种方法。在这个领域中还有一重要发现，即在某些情况下，发生在亚原子水平下的物理量离散，往往也能在微观情况下发生。量子霍尔效应是最近才发现的例子之一，即在电子和磁场力影响下的某些物质的电阻属性。

另一个重要研究是借此解释某些特殊现象，比如地心引力，都能用量子力学来解释。尽管还没有谁能证明地心引力的量子理论，但是物理学家认为这样的现象也许会出现在黑洞中或者是早期宇宙的某个地方。不管是通过爱因斯坦的非量子广义相对论还是量子场论的一般理念，都无法建立一个统一的重力量子理论。现在，许多物理学家都在寻找一种建立在弦理论上的方法，使得物体在一个空间维度中扩展，不同于拥有一般扩展名的粒子。弦理论也许在规定的量子力学的自然描述中，运用其他自然力正确定义重力。同时，毫无疑问，在人类思想启蒙的源头，量子力学是最成功的物理理论。

超弦理论和大统一理论

在理论物理中，超弦理论是一种数学建模，描述了非常短的基本粒子（大约10^（-35）米），即一维弦，而不是作为零维的点。这些弦被想象成可以扭曲、循环、合并以及分开。这些弦也被假设为存在在四个维度以上的空间内，并且还有其他的维度蜷缩在狭小的空间内。超弦理论被认为是非常投机的，没有得到认可，但是，对于范例的正确预测给了人希望，它也许最终能成为有关粒子和力量的独立理论。

在理论物理中，大统一理论（GUTs）尝试描述三种自然界的基础力，即作为一个单一的互动的单方面的强弱电磁力。大统一理论也描述了夸克和轻粒子关系的两个基本成分，它们表现为一个亚原子粒子的单一类型。

根据现有的定理，亚原子粒子之间的力是因为发射传输的途径和矢量玻色子的吸收形成的，这个粒子是一个单位的内在角动力。这些理论用于数学化的结构，被称为规范角动力，来描述这些基础相互作用。强弱电磁相互作用主要根据它们的力度来区分，如通过他们玻色子的一部分能量和玻色子可能释放出的能量进行测量。为了减少力度，个别的玻色子为胶子（强力的）、光子（电磁力的）以及W和Z粒子（弱力的）。

在大统一理论中，这些基础力量之间的差别可能是，在一个相对低能量的环境下，观察到的那些粒子的事实结果。如果粒子能够在非常大的能量下观察到，这三种相互作用将会有相等的力量。另外，夸克和轻粒子在这种条件下也会做相似的运动。在规定的期望值下，约10^（14）GeV（电子伏特），能量将会比现今的实验的能量高出一万亿倍。即使这种高能量的过程永远不可能在实验室中检测到，但是在原始宇宙中，比如宇宙大爆炸后的一秒内产生的能量，足够让所有粒子按照大一统理论所描述的那种方式运动。

一个令人意想不到的对与大一统理论的预测是，一个新的相互作用将产生，包括那些剩余能量有10^（14）电子伏特的矢量玻色子。这些相互作用能让三个夸克转变为一个轻子——包含了质子的衰变和由中子进入轻子。结果是，这样的衰变将会持续一个质子的寿命，即10^（31）电源年的时间，而且也有证据证明这会推到一个长期存有的概念，即质子将会长期稳定地存在。侦测那些很难发现的质子衰变的实验设计将会出现，但是还没有结论性的证据出来。

尽管大统一理论的有效性还没有得到认定，但是物理学家正在尝试把四种能量连接起来，即重力（它的玻色子和引力）以及其他三种能量，这被称作超对称理论。

物理理论中的对称性

在物理学中，如果一个系统在指定的操作中被认为不可变的话，那么它会呈现出一种对称性。如一个球在围绕它中心的任何方向旋转时，它看起来是一样的。这种情况下，这个球就被称为拥有球对称性。这种对称性在理解多种多样的物理现象中起到基础作用。在初级电子物理学中占有重要地位，但是起内在本质尚待研究。对称性的特征在于，即使没有内部作用的相关知识，根据其对称性，一个系统的许多方面是可以被预测的。

一个时光机器的发明者通过把一只家猫送到时间旅行中证明了此理论。来自雷•帕默尔（Ray Palmer）发表在《奇异故事》（Wonder Stories）上的《时空惨案》（The Time Tragedy）中的图解（1934年12月）。帕默尔之后成了《奇异故事》的编辑。这是一本从小事着手，并最终扩展到“命运”层次的杂志。其中讲述了许多时间旅行者的“真实”故事，以及其他超自然现象。

所有的对称性都可以分成两类，离散的和连续的。对于离散的对称，只有一个明确的运算能得到相同的物理形态：举个例子来说，就是在纸上画的一个正方形有一个离散对称，那是因为它有四条线，当它沿着一条垂直于纸平面的轴线旋转时，只在特定的位置看起来没有改变。但是，当在纸上画的圆在绕着垂直于纸的轴线旋转时，任何时候看起来是没有变化的。因此，圆展示了一个连续旋转的对称。

汤普森的时间旅行理论

此图解释了马尔科姆•史密斯（Malcolm Smith）在雷•帕默尔的《奇异故事》中讲的《汤普森的时间旅行理论》（Thompson’S Time Traveling Theory）的故事（1944）。在这个故事中，一个时光机器的发明者做了一个所谓的一个人回到过去，杀死了自己的祖父的祖父的悖论实验。

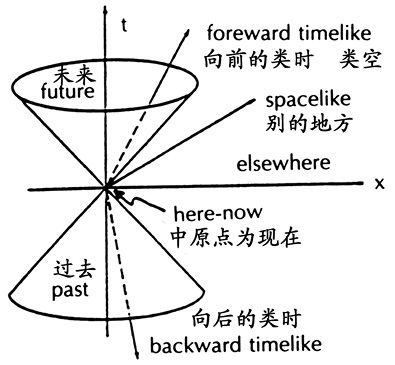
一个类空和类时世界的光椎图示（那金之后，1993）。

其他的一些有关连续对称的例子是时空的转化和旋转。前者指的是，就自然法则而言，在空间和时间上所有的点都是等价的。后者指的是在空间（空间的各向同性）各个方向都是等价的。离散对称的两个重要例子就是空间反演和时间反演不变性。一些自然法则在微小的反演和逆转的时间方向下是不会改变的。

守恒定律陈述了一个系统里的某些物理参数在时间进化过程中的不变性。例如，在经典物理学中（非相对论性的），一个系统的总质量在碰撞之前和之后都是固定不变的（质量守恒定律）。类似的，线动量和角动量以及一个系统的总动量在相对论性和非相对论性中都遵守守恒定律。

由于物理学上的拉格朗日表达式的出现，守恒定律的存在也和基本物理定律对称有关。例如，线动量的守恒是在空间转变下或者空间均一性下拉格朗日不变式的直接结果。角动量的守恒是旋转不变式的一个结果。在空间反演下的对称形成了同位一致性。

为了找出守恒定律的本质，我们需要研究在系统中力的性质和相关的对称性。因为所有的力都来自于其潜在的能量，所以通过潜在的能量来找出守恒定律的本质是可能的。比如，地球和太阳通过力的作用相互吸引，而这个力只是取决于这两者的距离而非它们的方向（一个中心力）。力的定律是不变的，因此可以得出角动量守恒。因为角动量的方向是垂直于旋转的平面的，因此地球和太阳永远固定在同一平面上。所以说，任意的两个物体之间都有一个中心力相互作用。

对称性仅限于某些最终的状态，一旦原始状态受到影响，反过来，也就暗示着最终状态在表面上是被禁止的。支配这种转变的定律被学术界称为选择性定律，这种定律在原子系统的研究中非常重要。

内在的对称和时空

目前为止，对称性的讨论涉及空间或者时间，或者两者同时涉及。某些对称性存在于“对称操作”把物质的一种状态改变成另一种状态时。比如，我们知道，在原子核中，同样的力存在于质子-质子，质子-中子和中子-中子中，这也就是说，在质子和中子中存在着一种物质的对称。在一个想象的“空间”中，质子和中子来自两个假设的方向，在一定空间的任意旋转不会影响原子核的稳定，这种特性被称为同位对称。在这样一个空间中包含的其他粒子形成了更高等的幺正对称性。内部对称的其他例子有电荷、重子数等等。这些内部的对称性基于一个虚拟的内部空间。

内部对称可在任一时空点上以相同或者不同的方式存在。人们把后一种情形称作规范对称性。在20世纪60年代，理论家把规范对称性应用于弱力和电磁力中。他们认为“自发对称性破坏”在理论上有着完美的对称性，然而在物理表现中却无法体现这一完美对称性。结果就是产生了一个包含两个力的弱电理论的单一数学模型。

我们所知的是，空间是由不同的维度构成的，而时间在这些维度中并不是以同样的方式存在。理论上讲，可以通过处理多维空间来穿越时间隧道。难以置信地是，物理学告诉我们，所有的东西都是通过不同的场进行内在连接的：引力场、电场、磁场、原子结构的弱力以及时间。时空旅行在理论上毫无障碍，甚至可以说，时空旅行和时空异常是整个宇宙的构成部分之一。

本章中的材料大多数来自于《葛罗里百科全书》（The Grolier Multimedia Encyclopedia),参考文献如下：

重力学参考文献：

伯格曼•P.G.的《引力之谜》（Bergmann.P.G.,The Riddle of Gravitation,1968)，霍金•S.W和以色列•W的《三百年万有引力史》（Hawking.S.W & Israel•W,Three Hundred Years of Gravitation,1987年初版，1989年再版），马修斯等编辑的《万有引力，量子场和超弦理论》（Mathews.P.M,Gravitation,Quantum Fields and Superstrings,1988），米斯纳•查尔斯等编著的《万有引力》（Misner Charles,Gravitation,1973)，国家研究委员会出版的《万有引力，宇宙论和宇宙射线物理》，（Gravitation，Cosmology and Cosmic-Ray Physics,1986)，索恩•K.S的《引力辐射》(Thorne K.S,Gravitational Radiation,1989)，安东尼的《一个老人的玩具》(Anthony,An Old Man's Toy,1989)。

相对论文献：

阿维尼•A的《时间帝国：日历，时钟和文化》（Aveni.A,Emipres of Time:Calendars,Clocks and Cultures,1989)，柯文尼•P和海菲尔德•R的《时间之箭》（Coveney.P,Highfield.R.,The Arrow of Time,1991)，柯恩•H.J的《时间及其测量：从石器时代到原子能时代》（Cowan•H.J,Time and Its Measurement:Form the Stone Age to the Nuclear Age,1958)，戴维斯•p的《有关时间：爱因斯坦未完成的革命》（Davies.P,About Time:Einstein's Unifnished Revolution,1995)，埃尔顿•L.R.B的《时间和人类》（Elton.L.R.B,Time and Man,1987)，弗拉德•R和洛克韦德•M合著的《时间的本质》（Flood.R,Lockwood.M,The Nature of Time,1987)，弗雷泽•J.T的《时间的发生及演变》（Fraser.J.T,The Genesis and Evolution of Time,1982)，豪斯•D的《格林尼治时和经度的发现》（Howse.D,Greenwich Time and the Discovery of the Longitude,1980)，科普契恩斯基•W和特劳特曼•A的《空间，时间以及万有引力》（Kopczynski.W,Trautman.A,Space,Time and Gravitation,1992)，普瓦德万•罗宾和麦克白•莫里合著的《时间的哲学》（Le Poidevin Robin,Macbeath Murray,The Philosophy of Time,1993)，欧玛莉•M的《保持警惕：美国时空史》（O'Malley.M,Keeping Watch:A History of Time in America,1990年初版，1991年再版），托尔敏S•V和古德菲儿德•J的《发现时间》（Toulmin.S.V,Goodfield.J,The Discovery of Time,1976年初版，1982年再版），惠特罗•G.J的《时间哲学的本质》（Whitrow.G.J,The Natural Philosophy of Time,第二版，1981)，安吉尔R.B的《相对论》（Angel.R.B,Relativity,1980)，波恩•马克思的《爱因斯坦的相对论》（Born Max,Einstein's Theory of Relativity,修订版，1962），蔡森•埃里克的《相对论说》（Chaisson Eric,Relativity Speaking，1990)，阿尔伯特•爱因斯坦的《相对论的意义》（The Meaning of Relativity,第五版，1956），加德纳•斯坦的《对爱因斯坦相对论的认知》（Gardner Stan,Understanding Einstein's Theory of Relativity,1991)，罗素•伯特兰的《相对论基础》（Russell Bertrand,The ABC of Relativity,第三版，1969年初版，1985年再版)，陶伯•G.E的《相对论》（Tauber.G.E.,Relativity,1988)，威尔•柯利弗德•M的《爱因斯坦是对的吗？》（Will Clifford.M,Was Einstein Right,1988)。

量子力学文献：

伯格•曼彼得•G的《相对论的入门》（Bergmann Peter.G,Introduction to the Theory of Relativity,1942年初版，1976年再版），德维加•H.J和桑德斯•N合著的《场论，量子引力和弦》（De Vega.H.J,Sanders.N,Field Theory,Quantum Gravity,and Strings,1986），阿尔伯特•爱因斯坦的《相对论的意义》（The Meaning of Relativity,第五版，1956），汉德罗克•查尔斯的《场论及其经典问题》（Hadlock Charles,Field Theory and Its Classical Problems,1979），莫哈帕特拉的《统一和超对称性》（Mohapatra,Unification and Supersymmetry,1986），托里雷特•玛丽的《爱因斯坦的统一场理论》（Tonnelat Marie,Einstein's Theory of Unified Fields,1966)，伯恩斯坦•杰里米的《量子剖面图》（Bernstein Jeremy,Quantum Profiles,1991），切斯特•马文的《量子力学的精华》（Chester Marvin,Prime of Quantum Mechanics,修订版，1992），费因伯格•杰拉尔德的《世界是由什么构成的？》（Feinberg Gerald,What Is the World Made Of,1977），韩•M.Y的《可能的宇宙》（Han.M.Y.,The Probable Universe,1992），希利•R.A的《量子力学的哲学》（Healey.R.A,The Philosophy of Quantum Mechanics,1991），赫伯特•尼克的《量子的真实性》（Herbert Nick,Quantum Reality,1985），杰梅尔•马克斯的《量子力学的概念发展》（Jammer Max,The Conceptual Development of Quantum Mechanics,1966），帕格尔斯•海因茨•R的《宇宙的密码》（Pagels Heinz R,The Cosmic Code,1982），惠勒•约翰和沃依切赫合著的《量子论及其测量》（Wheeler John,Woyciech,Quantum Theory and Measurement,1983）。

超弦理论文献：

彼得•弗洛伊德和马汉撒帕•K.T合著的《超弦》（Peter Frenud, Mahanthappa K.T,Superstrings,1988），盖茨和哈怕特拉•R.N合著的《超弦》（Gates,Mohapatra R.N,Superstrings,1987），林德莱•戴维的《最后的物理》（Lindley David,The End of Physics,1993），彼得•F.D的《超弦和对万物理论的搜寻》（Peat F.D,Superstrings and the Search for the Theory of Everything,1989），伯恩斯坦•杰里米的《第十维度》（Bernstein Jeremy,The Tenth Dimension,1989），费恩伯格•杰拉尔德的《世界是由什么构成的》，里切•哈拉尔德的《夸克》（Fritzsche Harald,Quarks,1983），帕格尔斯•海因茨的《宇宙的密码》和《完美的对称性》（Pagels Heinz,The Cosmic Code,1982年初版，1984年再版，Perfect Symmetry,1986），斯蒂文•温伯格的《亚原子粒子》（Steven Weinberg,Subatomic Particles,1983年初版，1990年再版）。

对称性文献：

布洛赫•彼得的《基本的对称性》（Bloch Peter,Fundamental Symmetries,1987），波特曼•艾伦等编著的《对称性及其在科学上的应用》（Boardman Allan,Symmetry and Its Applications in Science,1973），考克斯特的《几何学入门》（Coxeter,Introduction to Grometry,第二版，1989），•艾默生的《在粒子物理学中的对称性法则》（Emmerson,Symmetry Principles in Particle Physics,1972），加德纳•马丁的《通用的宇宙：镜子对称和时空扭转的世界》（Gardner Martin,The Ambidextrous Universe:Mirror Asymmetry and Time-Reversed Worlds,修订版，1979），利希滕贝格的《幺正对称性和初级粒子》（Lichtenberg,Unitary Symmetry and Elementary Particles,1978），路德维希和福尔特合著的《物理学上的对称》（Ludwig,Falter,Symmetries in Physics,1988），罗斯•杰里米的《对科学家而言的一个对称性的全盛时期》（Rosen J,A Symmetry Prime for Scientists,1983），韦尔•赫尔曼的《对称性》（Weyl Herman,Symmetry,1952），耶鲁•保罗•B的《几何学和对称性》（Yale Paul.B,Geometry and Symmetry,1968）。

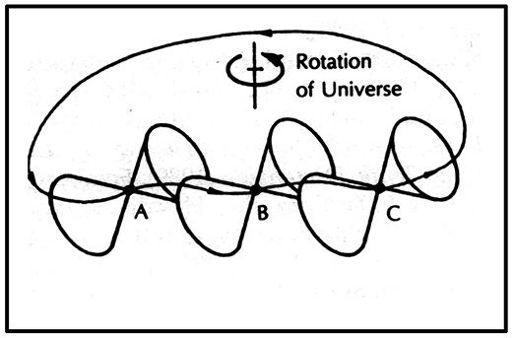
在旋转的宇宙中被叫做光锥（那金之后，1993年）

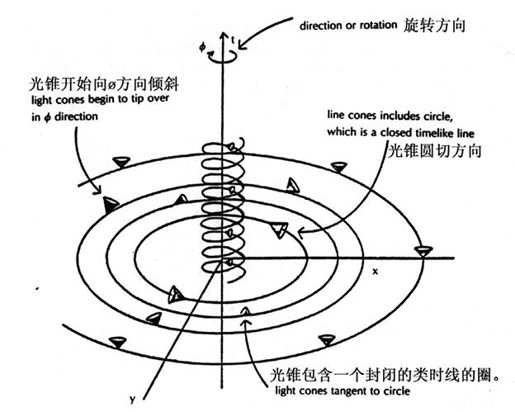
未来的光锥点几乎都在+t方位，远离旋转的物质；当物质靠近时，它们开始倾斜。注意：有一条螺旋型的类时线在局部移动，靠近未来-t的方位。换句话说，它由远离物质的观察者进入到过去。（整个世界旋转的物质都在+t方向上螺旋，那金之后，1993年）。

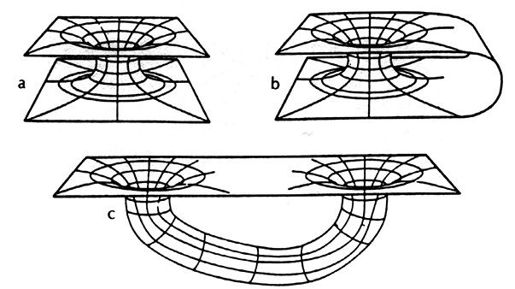
时光隧道和虫洞。这些不可避免地误导了对穿透三维空间的时间虫洞的解释。在a图中，虫洞连接了两个不相接的宇宙，然而在b和c图中，它们在同一个宇宙中相连接了。虫洞的“手柄”和两个洞口的外部距离相比既不太长也不太短。

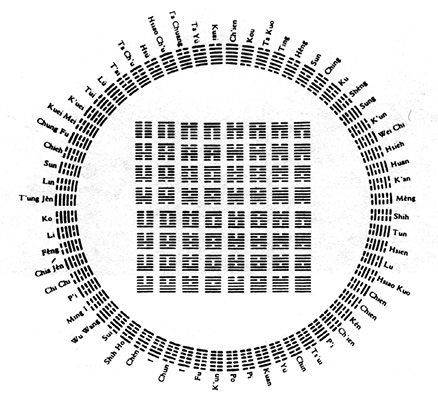
图片文字4：《易经》（I Ching）的六十四个六角线展示了一个圆和一个方形的传统排列。古代的先知认为具有这种形式的时光穿越，它通过对平行世界的一个二维解释能预测即将到来的事件或者允许使用者改变未来。

图片文字5:1969年，在佛罗里达州(Florida)的基韦斯特(Key West)附近，一个巨大的气旋龙卷风被美国国家海洋和大气管理局（NOAA)的航空器捕捉到。漩涡的出现很好地解释了三维的媒质是如何突然变成了横跨两个不同的时间和空间维度的一维漩涡丝。

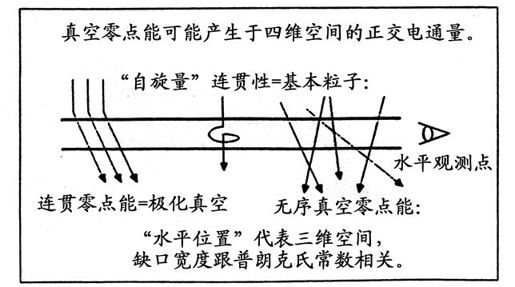
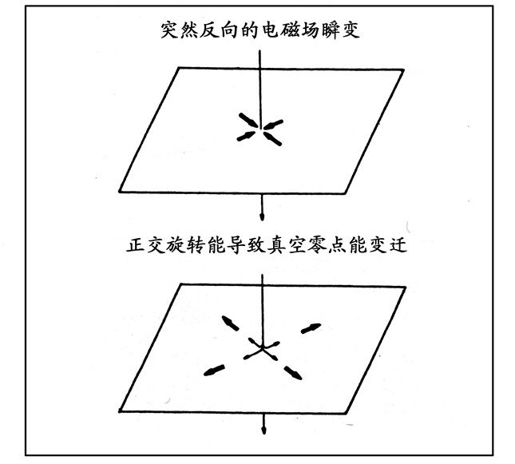
以上出自马里•B.金的《量子真空零点能》