第2章　MATLAB基础知识

本章介绍了MATLAB 7.0的一些基础知识，包括MATLAB的数据类型、基本矩阵操作、运算符和字符串处理函数。本章的知识是MATLAB 7.0编程的基础，熟练掌握了本章知识有利于学习后面的章节。

2.1　数据类型

MATLAB 7.0中定义了很多种数据类型，包括整数、浮点数、字符、字符串和逻辑类型等。用户甚至可以定义自己的数据类型。本小节讨论各种数据类型以及在MATLAB 7.0中使用它们的方法。

在MATLAB 7.0中有15种基本数据类型。每种基本的数据类型均以矩阵的形式出现，该矩阵可以是最小的0×0矩阵到任意大小的n维矩阵。数据类型结构如图2-1所示，其中带下划线的为基本数据类型。下面将依次介绍各种数据类型的用法。

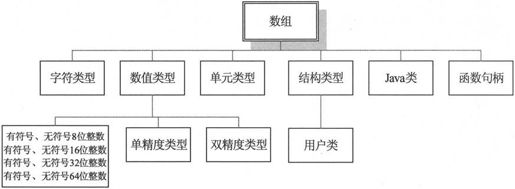
图2-1　数据类型结构图

2.1.1　数值类型

数值类型包含整数、浮点数和复数3种类型。另外MATLAB 7.0还定义了inf和NaN两个特殊数值。

1．整数类型

在MATLAB 7.0中整数类型包含4种有符号整数和4种无符号整数。有符号整数可以用来表示负数、零和正整数，而无符号整数则只可以用来表示零和正整数。MATLAB 7.0支持1、2、4和8字节的有符号整数和无符号整数。这8种数据类型的名称、表示方法和类型转换函数如表2-1所示。应用时要尽可能用字节数少的数据类型表示数据，这样可以节约存储空间和提高运算速度。例如最大值为100的数据可以用1个字节的整数来表示，而没有必要用8个字节的整数来表示。

表2-1　　　　　　整数的数据类型和表示范围

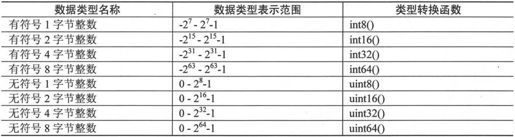
在表1-2中的类型转换函数可以用于把其他数据类型的数值强制转换为整数类型。此外类型转换函数还可以用于生成整数类型的数值。例如，如果需要产生一个有符号2字节整数的数值可以用如下语句实现，具体代码如下：

2．浮点数类型

MATLAB 7.0有双精度浮点数和单精度浮点数两种浮点数。双精度浮点数为MATLAB 7.0默认的数据类型。如果某个数据没有被显式地指定数据类型，那么MATLAB 7.0会用双精度浮点数来存储它。为了得到其他类型的数值类型，可以使用类型转换函数。

MATLAB 7.0中的双精度浮点数和单精度浮点数均采用IEEE 754中规定的格式来定义。其表示范围、存储大小和类型转换函数如表2-2所示。

表2-2　　　　　　浮点数的数据类型和表示范围

3．复数类型

复数包含独立的两部分，即实部和虚部。虚部的单位是-1的开平方根，在MATLAB 7.0中可以用i或者j来表示。

可以用如下赋值语句来产生复数：

也可以用函数complex来产生复数，示例代码如下：

其中x、y为实数，得到的z是以x为实部，y为虚部的复数。

也可以这样使用complex函数，具体代码如下：

其中x为实数，得到的z是以x为实部，以0为虚部的复数。

4．inf和NaN

MATLAB 7.0中规定用inf、-inf来表示正无穷大和负无穷大。除法运算中除数为0或者运算结果溢出都会导致inf或-inf的结果。以下3条语句运算产生的结果均为inf，具体代码如下：

MATLAB 7.0中规定用NaN来表示一个既不是实数也不是复数的数值。NaN是Not a Number的缩写。类似0/0、inf/inf这样的表达式得到的结果均为NaN。

2.1.2　逻辑类型

逻辑类型用1和0来表示true和false两种状态。可以用函数logical()来得到逻辑类型的数值。函数logical()可以把任何非零的数值转换为逻辑true（即1），把数值0转换为逻辑false（即0）。示例代码如下：

上述语句得到代码如下：

在2.3.2小节中将介绍的逻辑关系运算符也可以得到逻辑类型的数据。

2.1.3　字符和字符串

MATLAB 7.0中规定用数据类型char来表示一个字符。一个char类型的1×n数组则可以称为字符串string。MATLAB 7.0中char类型都是以2字节的unicode字符来存储的。

可以用一对单引号来表示字符串，例如下面的代码：

也可以用char函数来构造一个字符串，例如下面的代码：

上述语句得到字符串'AB'。

关于字符串的更深入的介绍请参考本书2.4小节。

2.1.4　函数句柄

函数句柄是MATLAB 7.0中用来提供间接调用函数的数据类型。函数句柄可以转递给其他函数以便该函数句柄所代表的函数可以被调用。函数句柄还可以被存储起来，以便以后利用。

函数句柄可以用符号＠后面跟着函数名来表示，例如下面的代码：

sin为MATLAB 7.0中自带的正弦函数，得到的输出变量fhandle为sin函数的句柄。可以利用fhandle来调用sin函数，例如下面的代码：

上面语句得到的输出代码如下：

实际上，该程序中的语句fhandle(0)相当于语句sin(0)。

2.1.5　结构体类型

结构体是根据属性名组织起来的不同类型数据的集合。有一种容易与结构体类型混淆的数据类型是单元数组类型，它是一种特殊类型的MATLAB 7.0数组，它的每一个元素叫做单元，而每一个单元包含MATLAB 7.0数组。结构体和单元数组的共同之处在于它们都提供了一种分级存储机制来存储不同类型的数据，不同之处是组织数据的方式不一样。结构体数组里的数据是通过属性名来引用的，而在单元数组里，数据是通过单元数组下标引用来操作的。本节将介绍结构体数组，而单元数组将在2.1.6小节中介绍。

结构体数组是一种由“数据容器”组成的MATLAB 7.0数组，这种“数据容器”称为结构体的属性（field）。结构体的任何一个属性可以包含任何一种类型的数据。如图2-2所示是一个结构体，它有所3个属性，即Name、Score和Salary，其中Name是一个字符串，Score是一个标量，Salary是一个1×5的向量。

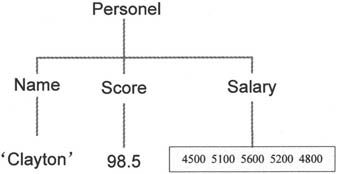
图2-2　结构体的属性

和其他的数据类型一样，结构体也是一种数组。一个单独的结构体就是一个1×1的结构体数组。用户可以构造任意维数和形状的结构体数组，当然也包含多维结构体数组。

1．结构体数组的构造

构造一个结构体数组有如下两种方法：

·　利用赋值语句；

·　利用函数struct()来进行定义。

下面就通过为结构体中的每一个属性赋值来构造一个结构体数组。例如，建立如图2-2所示的结构体数组Personel，可以用如下语句：

上述语句得到输出代码如下：

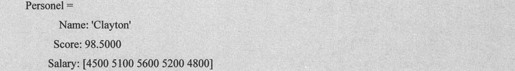
还可以用如下语句把结构体数组扩展成1×2的结构体，代码设置如下：

由上述语句使结构体数组Personel的维数变为1×2。当用户扩展结构体数组时，MATLAB 7.0对未指定数据的属性自动赋值成空矩阵，使其满足以下规则：

·　数组中的每个结构体都具有同样多的属性名；

·　数组中的每个结构体都具有相同的属性名。

例如，下面语句使结构体数组Personel的维数变为1×3，此时Personel(3).Score和Personel(3).Salary由于未指定数据，MATLAB 7.0将其设为空矩阵。

要注意的是结构体数组中元素属性的大小并不要求一致，例如结构数组Personel中的Name属性和Salary属性都具有不同的长度。

除了使用赋值语句来构造结构数组外，还可以用函数struct()来实现构造结构数组。函数struct的基本调用格式为：

上面语句中的输入变量为属性名和相应的属性值。

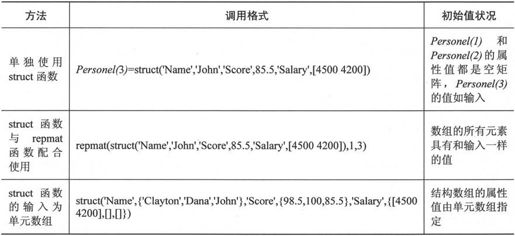
函数struct()可以有不同的调用方法来实现构造结构体矩阵，例如要实现一个1×3的结构数组Personel的方法如表2-3所示。

表2-3　　　　　　使用struct函数的方法

2．访问结构体数组的数据

使用结构体数组的下标引用，可以访问结构体数组任何元素及其属性。同样也可以给任何元素及其属性赋值。例如有一个结构体数组如图2-3所示，它可以通过下面语句来生成：

用户可以访问结构数组的任意子数组。例如，下面的命令行生成一个1×2的结构数组：

上述语句得到输出代码如下：

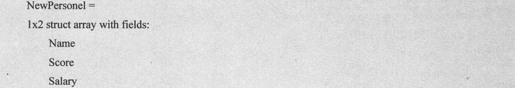
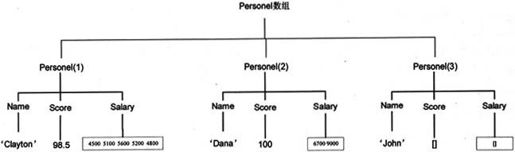
图2-3　结构数组

如果要访问结构体数组的某个元素的某个属性，可以用如下格式：

上述语句得到输出代码如下：

如果要访问结构体数组的某个元素的某个属性的元素值，可以使用如下格式：

上述语句得到的输出代码如下：

如果想得到结构体数组的所有元素的某个属性值，可以使用如下格式：

上述语句得到输出代码如下：

以上结果表明Personel.Name格式的输入将返回结构体数组的所有元素的属性值。可以使用矩阵合并符[]来合并这些结果，程序语句如下：

上述语句得到输出代码如下：

也可以用把它们合并在一个单元数组里，代码设置如下：

上述语句得到输出代码如下：

2.1.6　单元数组类型

单元数组就是每个元素为一个单元的数组。每个单元都可以包含任意数据类型的MATLAB 7.0数组。例如，单元数组的一个单元可以是一个实数矩阵，或是一个字符串数组，也可以是一个复向量数组。图2-4所示是一个2×3的单元数组，可见其每一个单元内的数据类型均不相同。

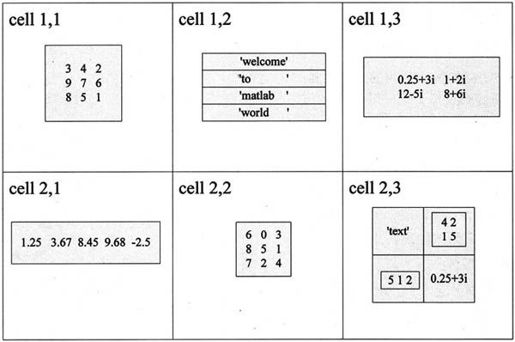
图2-4　单元数组示意图

1．单元数组的构造

构造单元数组有左标志法和右标志法两种方法。下面就详细介绍这两种方法。

·　左标志法

左标志法就是把单元标志{}放在左边，例如，创建一个2×2的单元数组可以使用如下语句：

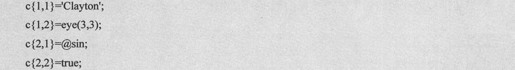
·　右标志法

右标志法就是把标志符放在右边，例如，创建和上面一样的单元数组可以使用如下语句：

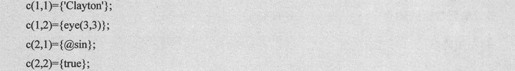
上述语句还可以简单地写为下面的代码：

要显示单元数组可以在命令行中直接输入单元数组的名字，代码设置如下：

由上述语句得到输出代码如下：

另一种显示单元数组的方法是使用函数celldisp()，代码如下：

由上述语句得到的输出代码如下：

值得注意的是函数celldisp()的显示格式与直接输入单元数组名的显示格式是不同的。celldisp()函数更适用于具有大量数据的单元数组的显示。

2．单元数组的读取

以上小节中的单元数组c作为例子。要读取c{1,1}中的字符串，可以使用如下语句：

由上述语句得到输出代码如下：

如果要读取单元数组的若干个单元的数据，例如读取单元数组C的第二行，可以用下面语句：

上述语句得到输出代码如下：

3．单元数组的删除

将空矩阵赋给单元数组的某一整行或者某一整列，就可以删除单元数组的这一行或者一列。

例如，删除单元数组c的第一行可以用如下语句：

上述语句得到输出代码如下：

2.2　基本矩阵操作

MATLAB 7.0是基于矩阵运算的一个软件，所有的数据均以二维矩阵或高维矩阵的形式存储，因此MATLAB 7.0又被称为矩阵实验室。

MATLAB 7.0中最基本的数据结构是二维的矩阵。二维的矩阵可以方便地存储和访问大量数据。每个矩阵的单元可以是数值类型、逻辑类型、字符类型或者其他任何的MATLAB 7.0数据类型。无论是单个数据还是一组数据，MATLAB 7.0均采用二维的矩阵来存储。对于一个数据，MATLAB 7.0用1×1矩阵来表示；对于一组数据，MATLAB 7.0用1×n矩阵来表示，其中n是这组数据的长度。MATLAB 7.0也支持多维的矩阵，MATLAB 7.0中称这类数据为多维数组（array）。

为了方便，把1×1的矩阵称为标量，把1×n的矩阵称为向量。把至少有一维的长度为0的矩阵称为空矩阵，空矩阵可以用[]来表示。

例如，实数1.5是1×1的双精度浮点数类型矩阵。在MATLAB 7.0中可以用语句whos来显示数值的数据类型和储存矩阵大小。以下语句可以用于查看实数1.5的数据类型和储存矩阵大小：

由上述语句得到输出代码如下：

例如，字符串'I am a great person'是1×19的字符矩阵类型矩阵，可以用如下语句来查看该字符串的数据类型和储存矩阵大小：

由上述语句得到输出代码如下：

2.2.1　矩阵的构造

1．简单矩阵构造

最简单的构造矩阵方法是采用矩阵构造符[]，构造一行的矩阵可以把矩阵元素放在矩阵构造符[]中，并以空格或者逗号来隔开它们，其代码设置如下：

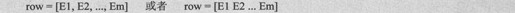
例如，一个1×4的矩阵可以通过如下语句得到：

或者是下面的代码：

如果矩阵是多行的，行与行之间用分号隔开，其代码设置如下：

例如一个3×4的矩阵可以用如下语句得到：

上述语句得到矩阵A如下：

2．特殊矩阵构造

MATLAB 7.0还提供一些函数用来构造一些特殊的矩阵，这些函数如表2-4所示。

表2-4　　　　　　特殊矩阵函数

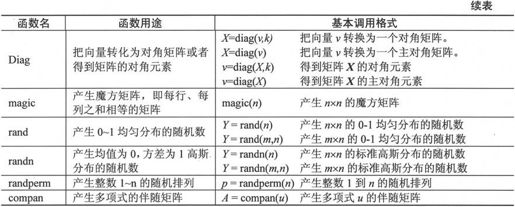
例如要产生一个3×4的全0矩阵，可以采用函数zeros()实现，代码设置如下：

由上述语句得到矩阵：

例如要产生一个1×5的0～1均匀分布的随机数，实现方法如下：

由上述语句得到矩阵：

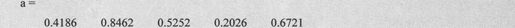
值得注意的是函数rand()是以机器时间作为随机种子的，每次运行上述语句得到的结果都是不同的。

3．向量的构造

向量在构造矩阵和对矩阵进行索引时是很有用的，因此MATLAB 7.0提供了专门用于产生向量的运算符——“:”。

冒号可以用来构造步长为1的递增向量，其格式为：

上式产生从a～b的以步长为1递增向量。例如：

上述语句生成的结果是：

向量中的元素不必是正整数，可以是任何整数。例如下面的代码：

由上述语句生成的结果是：

在默认的情况下，MATLAB 7.0总是保证步长精确地为1，即使在b值不是距离a值整数距离时也如此。例如下面的代码：

由上述语句生成的结果是：

如果b值小于a值，则MATLAB 7.0返回一个空矩阵。例如下面的代码：

由上述语句生成的结果是：

MATLAB 7.0也支持产生任意步长的向量，步长甚至可以是负数。例如下面的代码：

上面语句产生从0开始到pi结束的以1/4*pi为步长的向量。由上述语句生成的结果是：

例如：

上面语句产生从5开始到0结束的以-1为步长的向量。上述语句生成的结果是：

能够构造向量的其他函数还有linspace()函数和logspace()函数。Linspace()函数用于创建指定长度的等距向量。例如下面的代码：

上述语句产生-6，6之间等间距的4个点。由上述代码生成的结果是：

logspace()函数用于创建对数等距的向量，其使用方法与linspace()函数完全相同。

2.2.2　矩阵大小的改变

1．矩阵的合并

矩阵的合并就是把两个或者两个以上的矩阵数据连接起来得到一个新的矩阵。前面介绍的矩阵构造符[]不仅可用于构造矩阵，同时还可以作为一个矩阵合并操作符。表达式C＝[AB]在水平方向合并矩阵A和B，而表达式C＝[A;B]在竖直方向合并矩阵A和B。

例如：

由上述语句得到结果代码如下：

例如下面的代码：

由上述语句得到结果代码如下：

可以用矩阵合并符来构造任意大小的矩阵。不过需要注意的是在矩阵合并的过程中一定要保持矩阵的形状是方形，否则矩阵合并将无法进行。图2-5表明具有相同高度的两个矩阵可以在水平方向合并为一个新的矩阵。而图2-6则表明不具有相同高度的两个矩阵，不允许合并为一个矩阵。

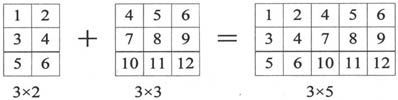
图2-5　正确的矩阵合并

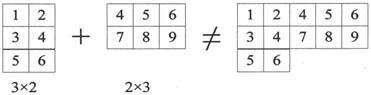
图2-6　不正确的矩阵合并

除了使用矩阵合并符[]来合并矩阵外，还可以使用矩阵合并函数来合并函数。这些矩阵合并函数的函数描述和基本调用格式如表2-5所示。

表2-5　　　　　　矩阵合并函数

例如下面的代码：

由上述语句得到输出代码如下：

又例如下面的代码：

由上述语句得到输出代码如下：

2．矩阵行列的删除

要删除矩阵的某一行或者是某一列，只要把该行或者该列赋予一个空矩阵[]即可。例如有一个4×4的魔方矩阵，代码设置如下：

上述语句得到矩阵A：

如果想删除矩阵的第2行，则可以用如下语句：

由上述语句得到新的矩阵A如下：

2.2.3　矩阵下标引用

本小节将介绍用矩阵下标来读取和改写矩阵元素的值的方法。包括如何用矩阵下标访问单个矩阵阵元素、如何线性引用矩阵元素、引用矩阵元素方式转换和访问多个矩阵元素。

1．矩阵下标访问单个矩阵阵元素

若A是一个2维矩阵，可以用A(i,j)来表示第i行第j列的元素。例如，假设A＝magic(3)，那么A(3,2)代表第3行第2列的数字。代码设置如下：

由上述语句得到输出代码如下：

也可以通过下标来改变矩阵的值，代码设置如下：

由上述语句得到新的矩阵A如下：

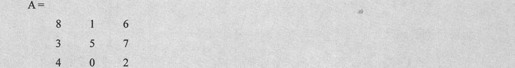
如果要访问多维矩阵可以通过指定多个下标来实现。

2．线性引用矩阵元素

在MATLAB 7.0中可以通过单下标来引用矩阵元素，其引用格式为A(k)。通常这样的引用是用于行向量或列向量。但是这样的引用也可以用于二维矩阵。MATLAB 7.0存储矩阵元素时并不是按照其命令行输出矩阵的格式来存储矩阵的。实际上，矩阵可以看成是按列优先排列的一个长列向量格式来存储的。例如下面的代码：

由上述语句得到矩阵：

矩阵A实际上在内存中是被存储成以2、4、3、6、2、5、9、8、1排列的一个列向量。A矩阵的第3行第2列，也就是值为5的元素实际上在存储空间是第6个元素。要访问这个元素，你可以用A(3,2)格式，也可以用A(6)格式。后者也就是线性引用矩阵元素方法。

一般地，设矩阵A是一个M×N的矩阵，矩阵元素A(i,j)如果换成用线性引用矩阵元素方法来表示可以表示为A((j－1)M＋i)。在上面的例子中A(3,2)＝A(2－1)3＋3)＝A(6)。

3．引用矩阵元素方式转换

如果你有矩阵的下标，但是你却想用线性引用矩阵元素方法来访问矩阵，你可以用sub2ind()函数来得到线性引用的下标。例如下面的代码：

由上述语句得到输出代码如下：

反之，如果想从线性引用的下标得到矩阵的下标可以用函数ind2sub()，例如下面的代码：

由上述语句得到输出代码如下：

4．访问多个矩阵元素

设A＝magic(4)，如果需要计算第4列元素的和，按照前面介绍的方法可以用下式来实现：

在下标表达式里，可以用冒号来表示矩阵的多个矩阵元素。例如，A(1:k,j)表示矩阵第j列的前k个元素。利用冒号，第4列元素的和可以用更为简洁的式子，代码设置如下：

还有更简洁的方法，因为冒号本身可以表示一列或者一行的所有元素，所以上式可以表达为：

在MATLAB 7.0中提供了一个关键字end，用于表示该维中的最后一个元素。所以上式还可以改写成：

实际上还可以用冒号来表示非相邻的多个元素，例如下面的代码：

由上述语句得到输出代码如下：

2.2.4　矩阵信息的获取

本小节介绍如何获取矩阵的信息，包括矩阵的尺寸大小，矩阵元素的数据类型和矩阵的数据结构。

1．矩阵尺寸信息

矩阵尺寸函数可以得到矩阵的形状和大小信息，这些函数如表2-6所示。

表2-6　　　　　　矩阵尺寸函数

下面例子用于表明如何使用矩阵尺寸信息获取函数。

设矩阵A为：

上述语句得到矩阵A如下：

求矩阵A的元素平均值可以用numel函数来实现，代码设置如下：

由上述语句得到均值如下：

在上式中sum(A(:))表示对A的所有元素求和，函数sum的用法将在第3章中介绍。

2．矩阵元素的数据类型

获得矩阵元素的数据类型信息的函数如表2-7所示。

表2-7　　　　　　获得矩阵元素的数据类型的函数

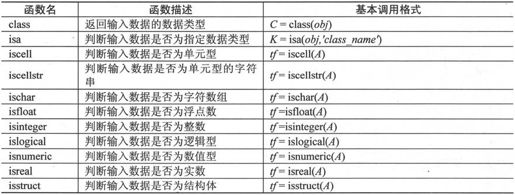
例如矩阵A是一个具有实数和复数的矩阵，如果需要将实数和复数分开，可以使用表2-7中的函数来实现，其方法如下：

由上述语句得到输出代码如下：

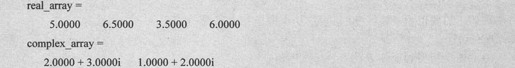
3．矩阵的数据结构

测试矩阵是否为某一种数据结构的函数如表2-8所示。

表2-8　　　　　　测试矩阵数据结构的函数

2.2.5　矩阵结构的改变

可以改变矩阵结构的函数如表2-9所示。

表2-9　　　　　　改变矩阵结构的函数

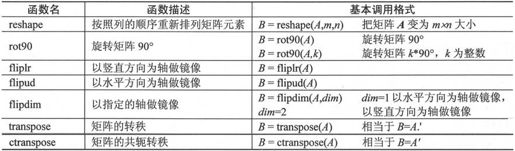
下面以一些例子来说明这些函数的用法。下面例子中的矩阵A均如下定义：

即矩阵A为：

例如，当要将一个3×4的矩阵按照列的顺序重新排列成2×6的矩阵时，可以用下列语句来实现：

由上述语句得到矩阵B为：

例如，需要把矩阵旋转90°，可以用下面语句来实现：

由上述语句得到矩阵B为：

例如，需要把矩阵以竖直方向为轴做镜像，可以用下面语句来实现：

由上述语句得到矩阵B为：

2.2.6　稀疏矩阵

在MATLAB 7.0中可以用两种方式来存储矩阵，即满矩阵存储方式和稀疏矩阵存储方式，简称满矩阵和稀疏矩阵。

在很多情况下一个矩阵只有少数的元素是非零的，而前面的章节中介绍的矩阵对于零值和非零值是花费同样空间来存储的，因此这种存储方式会浪费很多存储空间，有时还会减慢计算的速度。这种存储方式称为满矩阵存储方式。而稀疏矩阵在MATLAB 7.0内部是以非零元素和非零元素的行列指标数组来表示的。因此，稀疏矩阵提供了一种针对矩阵元素大多数都是零值矩阵的有效存储方式。

用户可以创建双精度类型、复数类型和逻辑类型的稀疏矩阵，所有MATLAB 7.0自带的数学函数、逻辑函数和引用操作均可以使用在稀疏矩阵上。稀疏矩阵不能自动生成，定义在满矩阵的运算只能生成满矩阵，不论多少个元素为零。但是，一旦以稀疏矩阵来存储，那么稀疏矩阵的存储方式就会传播下去。即定义在稀疏矩阵上的运算生成稀疏矩阵，定义在满矩阵上的运算生成满矩阵。

1．稀疏矩阵的存储方式

MATLAB 7.0内部使用3个矩阵来存储稀疏矩阵。设有一个m×n的矩阵有nnz个非零元素，存储在长度为nzmax的矩阵中。

·　第1个矩阵存储着所有的非零元素，该矩阵的长度为nzmax；

·　第2个矩阵存储着所有的非零元素的行指标，该矩阵的长度也为nzmax；

·　第3个矩阵存储着每一列的开始处指针和一个标志着这3个矩阵结束的指针，该矩阵的长度为n＋1。

一个稀疏矩阵要求存储nzmax个浮点数和nzmax＋n＋1个整数，因此存储一个稀疏矩阵需要8nzmax＋4(nzmax＋n＋1)个字节的单元。

复数类型的稀疏矩阵用第4个矩阵来存储非零元素的虚部。一个复数只要其实部和虚部的其中一个为非零元素，该复数就是非零。

2．稀疏矩阵的创建

MATLAB 7.0提供转换函数可以从满矩阵得到稀疏矩阵，即sparse()函数。其调用格式为S＝sparse(A)，其中A为满矩阵。例如下面的示例代码：

由上述语句得到输出代码如下：

把一个稀疏矩阵转换为一个满矩阵，可以用转换函数full()。例如下面的示例代码：

由上面语句返回得到矩阵A。

还可以用sparse()函数来直接创建稀疏矩阵，其调用格式为S＝sparse(i,j,s,m,n)，其中i和j分别是稀疏矩阵非零元素的行和列指标，s为相应的非零元素的值。m和n分别是矩阵的行高度和列高度。上述稀疏矩阵可以用直接方法创建，语句如下：

由上述语句得到输出代码如下：

MATLAB 7.0还提供一些函数用于创建一些特殊的稀疏矩阵，这些函数如表2-10所示。

表2-10　　　　　　特殊稀疏矩阵创建函数

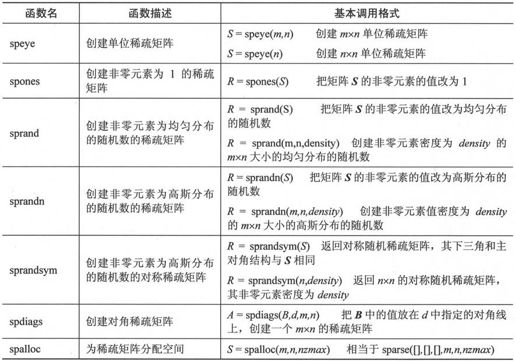
还可以将外部的稀疏矩阵转换成为内部的形式。如果ASCII码文件中存有一个稀疏矩阵的[i,j,v]，即非零值的行列指标和非零值，则可以用load()函数把该文件加载到MATLAB 7.0空间，然后用函数spconvert()把它转换为稀疏矩阵。例如，文件t.dat的内容如下：

然后用如下语句得到稀疏矩阵：

上述语句得到输出代码如下：

3．查看稀疏矩阵

MATLAB 7.0还提供一些函数，用于得到稀疏矩阵的定量信息和图形化信息。这些函数包括得到稀疏矩阵非零值信息和图形化稀疏矩阵。

查看稀疏矩阵非零值信息的函数如表2-11所示。

表2-11　　　　　　查看稀疏矩阵非零值信息的函数

为了尝试上面函数的用法，可以加载MATLAB 7.0自带的稀疏矩阵west0479，代码设置如下：

由上述语句得到输出代码如下：

为了得到该矩阵非零值的个数，可以用如下语句：

由上述语句得到输出代码如下：

为了得到用于存储非零值的空间长度，可以用如下语句：

上述语句得到输出如下：

有时用图形来显示矩阵非零值的分布是很有用的，在MATLAB 7.0中spy()函数实现了这一功能。为了查看稀疏矩阵west0479的非零值的分布，可以用如下语句：

由上述语句得到如图2-7所示的图形。

图2-7　稀疏矩阵图

4．稀疏矩阵的运算规则

在MATLAB 7.0系统中的各种命令都可以用于稀疏矩阵的运算。但有稀疏矩阵参加运算时，所得到的结果将遵循以下的规则：

·　把矩阵变为标量或者定长向量的函数总是给出满矩阵；

·　把标量或者定长向量变换到矩阵的函数（zeros()、ones()、eye()、rand()等）总是给出满矩阵；而能给出稀疏矩阵结果的相应的函数有speye()和sprand()等；

·　从矩阵到矩阵或者向量的变换函数将以原矩阵的形式出现。即定义在稀疏矩阵上的运算生成稀疏矩阵，定义在满矩阵上的运算生成满矩阵。例如chol(S)、max(S)和sum(S)等函数；

·　两个矩阵运算符（如+、-、、\、|）操作后的结果一般都是满矩阵，除非参加运算的矩阵都是稀疏矩阵，或者操作本身（如.，&）保留矩阵的稀疏性；

·　参与的矩阵扩展（如[A B;C D]）的子矩阵中，只要有一个是稀疏的，那么所得的结果也是稀疏的；

·　在矩阵引用中，将仍以原矩阵形式给出结果。若S矩阵是稀疏的，而Y矩阵是全元素的，不管I、J是标量还是向量，那么“右引用”Y＝S(I,J)产生稀疏矩阵，而“左引用”S(I,J)＝Y产生满矩阵。

2.3　运算符和特殊符号

MATLAB 7.0中提供了丰富的运算符，非常方便地满足用户的各种应用。这些运算符包括算数运算符、关系运算符和逻辑运算符三种运算符。

2.3.1　算数运算符

MATLAB 7.0的算数运算符的用法和功能如表2-12所示。

表2-12　　　　　　算数运算符的用法和功能

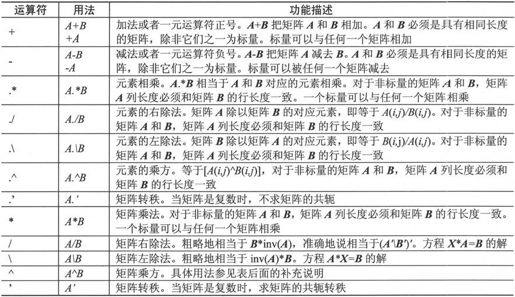
补充说明符号＾的用法如下：

当A和B都是标量时，表示标量A的B次方幂。当A为方阵，B为正整数时，表示矩阵A的B次乘积；B为负整数时，表示矩阵A的逆的B次乘积。当B为非整数时，有如下表达式：

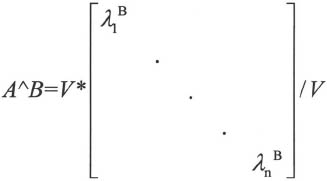
其中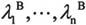为矩阵A的特征值，V为对应的特征向量矩阵。当A为标量，B为方阵时，有如下表达式：

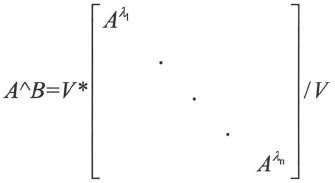
其中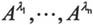为方阵B的特征值，V为对应的特征向量矩阵。当矩阵A和矩阵B都为矩阵时，此运算无定义。

除了某些矩阵运算符，MATLAB 7.0的算数运算符只对相同规模的数组作相应的运算。对于向量和矩阵，两个操作数必须同规模或者有一个操作数为标量。如果一个操作数是标量，而另外一个不是，MATLAB 7.0会将这个标量与另一个操作数的每一个元素进行运算。

例如：

上述语句得到矩阵如下：

在命令行输入语句如下：

上述语句得到输出代码如下：

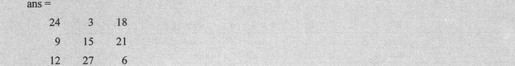
与以往的MATLAB版本不同的是，MATLAB 7.0的数学运算符不但支持双精度数据类型的运算，还增加了对单精度类型、1字节无符号整数、1字节有符号整数、2字节无符号整数、2字节有符号整数、4字节无符号整数和4字节有符号整数运算的支持。

2.3.2　关系运算符

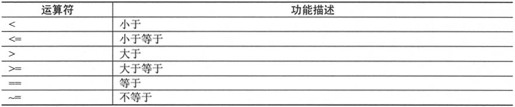
MATLAB 7.0的关系运算符的用法和功能如表2-13所示。

表2-13　　　　　　关系运算符

MATLAB 7.0的关系运算符只对具有相同规模的两个操作数或者其中一个操作数为标量的操作数进行操作。当两个操作数具有相同规模时，MATLAB 7.0对两个矩阵的对应元素进行比较，返回的结果是与操作数具有相同规模的矩阵。例如，下面的示例代码比较3×3魔方矩阵中哪些元素的值大于4。

上述语句得到输出代码如下：

返回结果中等于1的位置上，表示此处magic(3)的矩阵元素大于4。

当其中一个操作数是标量时，MATLAB 7.0将标量与另一个操作数的每一个元素进行比较，返回结果是与非标量操作数具有相同规模的矩阵。例如，上面的示例也可以用矩阵与标量进行关系运算来实现，语句如下：

当检验一个矩阵是否是空矩阵时，或许会想到用关系式A==[]。但是如果A不是0×0或1×1的话，将返回警告信息。MATLAB 7.0提供了一个函数isempty()专门用于判断一个矩阵是否为空矩阵，例如要检验A是否为空矩阵，可以用语句isempty(A)。如果A为空矩阵则返回1，否则返回0。

2.3.3　逻辑运算符

MATLAB 7.0提供3种类型的逻辑运算符，即元素方式逻辑运算符、比特方式逻辑运算符和短路逻辑运算符。

元素方式逻辑运算符的用法和功能如表2-14所示。元素方式逻辑运算符只接受逻辑类型变量输入。表中例子采用如下矩阵：

表2-14　　　　　　元素方式逻辑运算符

MATLAB 7.0的元素方式逻辑运算符只对具有相同规模的两个操作数或者其中一个操作数为标量的操作数进行操作。

元素方式逻辑运算符有重载的函数，实际上符号'&'、'|'和'～'的重载函数分别是and()、or()和not()。

比特方式逻辑运算符对操作数的每一个比特位进行逻辑操作，其用法和功能如表2-15所示。比特方式逻辑运算符接受逻辑类型和非负整数变量输入。

表中例子采用如下矩阵：

表2-15　　　　　　比特方式逻辑运算符

MATLAB 7.0的短路逻辑操作符用法和功能如表2-16所示。

表2-16　　　　　　短路逻辑运算符

短路逻辑运算符的运算结果和元素方式逻辑运算符的运算结果是一样的。然而短路逻辑运算符在执行时，只有在运算结果还不确定时才去参考第二个操作数。例如，A&&B操作，当A为0时，直接返回0，而不检查B的值；当A为1时，如果B为1，则返回1，否则返回0。A‖B的执行方式也与A&&B类似。

有些情况下，需要满足特定条件，才能被执行的语句，可以用短路逻辑运算符来实现。例如，下面语句实现判断是否a／b＞1，当b为0时也不会出错。当b＝0时，函数直接返回0，而不计算a／b。

2.3.4　运算优先级

用户编写的表达式可以包括算术运算符、关系运算符和逻辑运算符。因此运算符的优先级决定了对一个表达式的求值顺序。具有相同优先级的运算符则从左到右依次进行运算；不同优先级的运算符则先进行高优先级运算。运算符的优先等级如表2-17所示。

表2-17　　　　　　运算符的优先等级

由表2-17中可以看到，括号的优先级别最高，因此可以用括号来改变默认的优先等级，例如下面的示例代码：

上述语句得到输出代码如下：

而采用括号后的语句如下：

上述语句输出结果代码如下：

2.4　字符串处理函数

本节介绍字符串处理函数。字符串是指1×n的字符数组。

MATLAB 7.0能够很好地支持字符串数据，用户可以用两个不同的方式来表示字符串，即字符数组和字符串单元数组。用户可以用m×n的字符数组来表示多个字符串，只要这些字符串的长度是一样。当需要保存多个不同长度的字符串时，可以用单元类型来实现。

MATLAB 7.0提供了很多字符串操作，包括字符串的创建、合并、比较、查找以及与数值之间的转换。

2.4.1　字符串的构造

1．创建字符数组

可以用一对单引号来表示字符串，例如下面的示例代码：

也可以用字符串合并函数strcat()来得到一个新的字符串，例如下面的示例代码：

上述语句得到输出代码如下：

值得注意的是，函数strcat()在合并字符串的同时会把字符串结尾的空格删除。要保留这些空格，可以用矩阵合并符[]来实现字符串合并，例如下面的示例代码：

上述语句得到输出代码如下：

用户也可以构造二维字符数组，不过要注意保持二维字符数组的每一行具有相同的长度。例如，下面字符串是合法的，因为它的每行都有6个字符：

上述语句得到输出代码如下：

当构造的多个字符串具有不同长度时，可以在字符串的尾部添加空格来强制实现字符串具有相同的长度。

例如下面的示例代码：

上述语句得到输出代码如下：

一个更简单的方法是利用函数char()来创建字符串。该函数创建字符串数组时，如果字符串不具有相同的长度，则函数char()自动用空格把字符串补足到最长的字符串的长度。例如下面的示例代码：

上述语句得到输出代码如下：

与函数char()具有类似功能的函数是strvcat()。函数strvcat()把多个字符串合并为一个字符串数组。当字符串不具有相同长度时，函数strvcat()自动在尾部添加空格补足到最长的字符串的长度。例如下面的示例代码：

上述语句得到输出代码如下：

2．创建字符串单元数组

可以用函数cellstr()来创建字符串单元数组。例如，有一个字符数组如下：

上述语句得到输出代码如下：

下面语句的功能是把上述字符数组转换成为字符串单元数组，示例代码设置如下：

上述语句得到输出代码如下：

注意，函数cellstr()已经把字符串尾部的空格截去。可以查看celldata的第一个字符串长度如下：

上述语句得到输出代码如下：

可以用函数char()把一个字符串单元数组转换成一个字符数组，示例代码设置如下：

上述语句得到输出代码如下：

其第一个字符串的长度可以得到如下的代码：

上述语句得到输出代码如下：

2.4.2　字符串比较函数

MATLAB 7.0里包括以下几种比较字符串和字符子串的方法。比较两个字符串或者两个字符串的子串是否相同。

·　比较两个字符串中的单独字符是否相同；

·　对字符串内的元素进行识别，判定每一个元素是字符还是空白符（包括空格、制表符Tab和换行符）。

这些函数对字符数组和字符串数组都适用。

1．字符串比较函数

MATLAB 7.0为用户提供的字符串比较函数如表2-18所示。

表2-18　　　　　　字符串比较函数

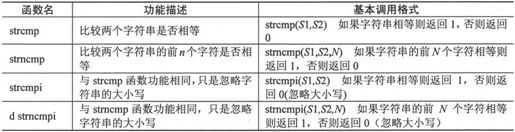
例如，有两个字符串如下：

由于这两个字符串不相同，故调用函数strsmp()的结果为0，语句如下：

上述语句得到输出代码如下：

这两个字符串的前3个字符是相同的，故用函数strncmp()比较它们的前3个字符，会返回1，代码设置如下：

上述语句得到输出代码如下：

2．用关系运算符比较字符串

可以对字符数组运用MATLAB 7.0的关系运算符，但是要求比较的字符数组具有相同的维数，或者是其中一个是标量。例如，可以用等号运算符（==）来判断两个字符串里哪些字符是相同的。

上述语句得到输出代码如下：

当然，还可以用其他关系运算符（>、>=、<、<=、==、!=）来比较两个字符串。

2.4.3　字符串查找和替换函数

MATLAB 7.0为用户提供的一般字符串查找和替换函数如表2-19所示。

表2-19　　　　　　字符串查找和替换函数

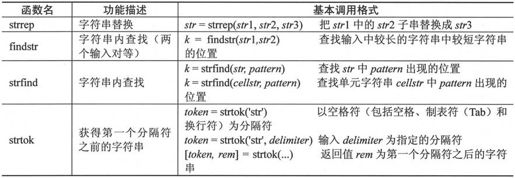
下面例子是实现字符串替换：

上述语句得到输出代码如下：

下面例子是用于实现字符串查找：

上述语句得到输出代码如下：

下面例子是用于获得第一个分隔符之前的字符串：

上述语句得到输出代码如下：

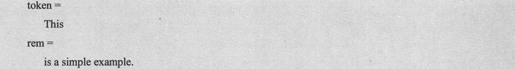
下面例子是用于实现字符串匹配：

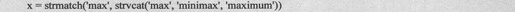
上述语句得到输出代码如下：

2.4.4　字符串——数值转换

MATLAB 7.0为用户提供的把数值转换为字符串的函数如表2-20所示。

表2-20　　　　　　数值转换为字符串的函数

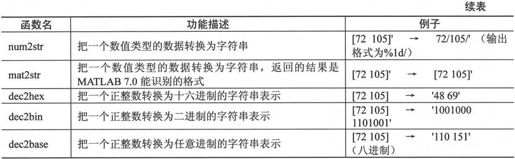
MATLAB 7.0为用户提供的把字符串转换为数值的函数如表2-21所示。

表2-21　　　　　　字符串转换为数值的函数

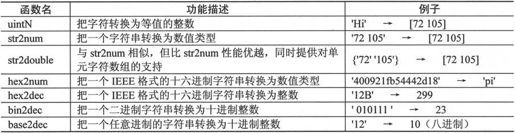
例如，要在命令行中输出一行字符串来显示向量x的最大值，可以用如下程序：

其中函数disp()是在命令行中显示一个字符串。由上述语句得到的输出代码如下：