第8章　MATLAB 7.0符号计算功能

符号数学工具箱中的工具是建立在功能强大的Maple软件的基础上。它最初是由加拿大的滑铁卢（Waterloo）大学开发出来的。如果要求MATLAB 7.0进行符号运算，那么首先由Maple计算并将结果返回到MATLAB 7.0命令窗口。因此可以说MATLAB 7.0中的符号运算是它处理数字运算的自然扩展。

进行符号计算，第一，计算以推理解析的方式进行，因此不受计算误差累积所带来的困扰；第二，符号计算可以给出完全正确的封闭解或任意精度的数值解（当封闭解不存在时）；第三，符号计算指令的调用比较简单，与经典教科书公式相近；第四，计算所需要的时间较长。

在MATLAB 7.0中，符号计算虽以数值计算的补充身份出现，但设计符号计算的相关指令、符号计算结果的图形化显示、符号计算程序的编写以及在线帮助系统都是十分完整和便捷的。

MATLAB 7.0的升级和符号计算内核Maple的升级，决定了符号计算工具包的升级。但从用户使用的角度来看，这些升级所带来的变化相当细微。本章在相关的部分也给出了声明。

8.1　符号运算入门

科学与工程技术中的数值运算固然重要，但自然科学理论分析中各种各样的公式、关系式及其推导就是符号运算要解决的问题。它与数值运算一样，都是科学计算研究的重要内容。MATLAB 7.0数值运算的对象是数值，而MATLAB 7.0符号运算的对象则是非数值的符号对象。所谓符号对象就是指代表非数值的符号字符串。下面列举一些实例来具体说明MATLAB7.0的符号运算功能。

8.1.1　求解一元二次方程x²＋2x＋2＝0的根

这是一个求解一元二次方程数值根的数字计算问题。根据求根公式，很容易得到方程的两个数值根是x_1,2＝-1±j。

而对于一元二次方程一般式ax²＋bx＋c＝0来说，要求它的根，就必须根据一元二次方程求根公式，得到方程的根为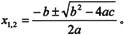这就是一个求一元二次方程根的符号运算问题。

MATLAB 7.0里的符号运算功能正是用来解决这类问题的。只要运行以下的函数命令：

即可求得一元二次方程的两个根：

求解一元二次方程数值根的计算问题也可以运行相同的MATLAB 7.0函数命令。例如求方程x²＋2x＋2＝0的根时，可运行如下的语句：

即可得到方程的根：

8.1.2　求导数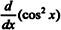

根据复合函数求导公式，有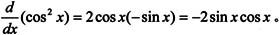可以运行以下MATLAB 7.0语句求复合函数的导数：

即可求得导数：

8.1.3　计算定积分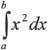

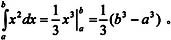计算定积分即做运算可以运行以下两条MATLAB 7.0语句：

即得到定积分的结果：

8.1.4　求解一阶微分方程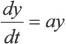

即作运算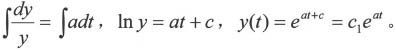

可以运行以下MATLAB 7.0语句：

即求得一阶微分方程的解：

从以上几个例子可以看出MATLAB 7.0符号运算的对象全是文字符号，算得的结果也是文字符号，同时符号运算基本上覆盖了初等数学以及高等数学中的绝大多数内容，而且这些运算都能够用MATLAB 7.0函数命令行来实现。

8.2　符号对象的创建和使用

符号数学工具箱中定义了一种新的数据类型，叫sym类。sym类的实例就是符号对象，符号对象是一种数据结构，是用来存储代表符号的字符串的。在符号数学工具箱中，用符号对象来表示符号变量、符号表达式和符号矩阵。

本节将介绍如何借助MATLAB 7.0的符号数学工具箱来创建和使用符号变量、符号表达式和符号矩阵，同时介绍MATLAB 7.0的默认符号变量及其设置方法。

8.2.1　创建符号对象和表达式

在一个MATLAB 7.0程序中，作为符号对象的符号常量、符号变量、符号函数以及符号表达式，可以使用函数命令sym()、syms()加以规定和创建，利用class()可以测试建立的操作对象为何种操作对象类型以及是否为符号对象类型。

（1）函数命令sym()

函数命令sym()的调用格式有如下两种：

命令公式是由A来建立一个符号对象S，其类型为sym类型。如果A（不带单引号）是一个数字、数值矩阵或数值表达式，则输出是将数值对象转换成的符号对象。如果A（带单引号）是一个字符串，输出则是将字符串转换成的符号对象。

其中flag为转换的符号对象应该符合的格式。如果被转换的对象为数值对象，flag可以有如下选择：

·　'd'—最接近的十进制浮点精确表示；

·　'e'—带（数值计算时）估计误差的有理表示；

·　'f'—十六进制浮点表示；

·　'r'—为缺省设置时，最接近有理表示的形式。

对于被转换对象为字符串时，flag有如下几种选项：

·　'positive'—限定A为正的实型符号变量；

·　'real'—限定A为实型符号变量；

·　'unreal'—限定A为非实型符号变量。

（2）函数命令syms()

函数命令syms()的调用格式为：

该命令可以建立3个或多个符号对象，如s1、s2、s3。同样，flag为对转换格式的限定，具体选项同上。

（3）函数命令class()

函数命令class()的调用格式如下：

class()命令将返回对象的数据类型。

以下就分别来介绍在不同情况下这些函数的具体使用方法。

1．符号常量

符号常量是一种符号对象。数值常量如果作为函数命令sym()的输入参量，这就建立了一个符号对象——符号常量，虽然看上去它是一个数值量，但它已是一个符号对象了。创建这个符号对象可以用class()函数来检测其数据类型。

【例8.1】对数值3/4创建符号对象并检测数据的类型。

【解】可以用以下MATLAB 7.0语句来创建符号对象并检测数据的类型：

语句的执行结果为：

即a实双精度浮点数值类型；b实字符类型；c和d都是符号对象类型。

2．符号变量

变量是程序语言的基本元素之一。MATLAB 7.0符号运算中，符号变量是内容可变的符号对象。符号变量通常是指一个或几个特定的字符，不是指符号表达式，甚至可以将一个符号表达式赋值给一个符号变量。符号变量有时也称为自由变量。符号变量与MATLAB 7.0数值变量名称的命名规则相同：

·　变量名可以由英文字母、数字和下划线组成；

·　变量名应以英语字母开头；

·　组成变量名的字母长度不大于31个；

·　MATLAB 7.0中区分大小写英语字母。

在MATLAB 7.0中可以用函数命令sym()和syms()来建立符号变量。

【例8.2】用函数命令sym()和syms()建立符号变量a、b、c。

【解】

（1）用函数命令sym()来创建符号对象并检测数据的类型

用sym()命令来创建符号对象并检测数据类型的代码如下：

语句执行的结果如下：

可以看出得到的3个变量均为符号对象。

（2）用函数命令syms()来创建符号对象并检测数据的类型

用syms()命令来创建符号对象并检测数据类型的代码如下：

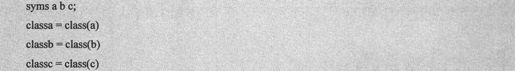
语句执行的结果如下：

从上面的两种实现方法可以看出，对于需要同时定义多个符号变量的情况，使用sym()命令分别定义显得过于繁琐，而可以采用syms()命令进行代替。MATLAB 7.0提倡用syms()命令，因为它需要很少的书写，比较符合MATLAB 7.0符号运算简洁的特点。

3．符号表达式、符号函数与符号方程

表达式也是程序设计语言的基本元素之一。在MATLAB 7.0符号运算中，符号表达式是由符号常量、符号变量、符号函数运算符以及专用函数连接起来的符号对象。符号表达式有两类：符号函数与符号方程。符号函数不带等号，而符号方程是带等号的。

在MATLAB 7.0中，同样采用命令sym()或syms()来建立符号表达式。下面看一个建立符号函数的例子。

【例8.3】用函数命令sym()与syms()建立符号函数f1、f2、f3。

【解】用函数命令sym()与syms()来创建符号函数：

【例8.4】用函数命令sym()来创建符号方程e1、e2、e3。

【解】具体的实现命令如下：

4．符号矩阵

元素是符号对象（非数值符号的字符符号即符号变量与符号形式的数即符号常量）的矩阵叫做符号矩阵。符号矩阵既可以构成符号矩阵函数，也可以构成符号矩阵方程，它们都是符号表达式。

【例8.5】用函数命令sym()建立符号矩阵m1、m2。

【解】具体的实现命令如下：

从上面的例子可以看出，创建符号矩阵的方法可以概括为两种：sym()指令直接输入法，如m1的实现；数值矩阵转换法，如m2。这里需要重点指出的是第二种方法，数值矩阵转换法，把这种方法同MATLAB 7.0种许多数值矩阵的生成函数配合起来，可以产生出许多特殊的符号矩阵。

8.2.2　符号对象的基本运算

由于新版MATLAB 7.0采用了重载技术，使得构称符号计算表达式的运算符和基本函数，无论在形状、名称上，还是在使用方法上，都与数值计算中的运算符和基本函数几乎完全相同。这无疑给用户带来了极大的方便。

下面就符号计算种的基本算符和函数作一些简要的归纳。

1．基本运算符

·　运算符“+”、“-”、“*”、“\”、“/”、“^”分别实现矩阵的加、减、乘、左除、右除和求幂运算。

·　运算符“.*”、“./”、“.\”、“.^”分别实现“元素对元素”的数组乘、左除、右除和求幂运算。

·　运算符“'”、“.'”分别实现矩阵的共轭转置和非共轭转置。

2．关系运算符

在符号对象的比较中，没有“大于”、“大于等于”、“小于”和“小于等于”的概念，而只有是否“等于”的概念。

运算符“＝＝”和“～＝”分别对运算符两边的对象进行“相等”、“不等”的比较。当事实为“真”时，返回结果1；否则，返回结果0。

3．三角函数、双曲函数以及它们的反函数

除atan2仅能用于数值计算外，其余的三角函数（如sin）、双曲函数（如cosh）及它们的反函数（如asin、acosh），无论在数值计算还是在符号计算中，它们的使用方法都相同。

4．指数、对数函数

在数值、符号计算中，函数sqrt、exp和expm的使用方法完全相同。至于对数函数，在MATLAB 6.X版本中，符号计算中只有自然对数log，而没有数值计算中的log2、log10。而在MATLAB 7.X版本中，增加了log2和log10函数，其用法同数值运算中完全相同。

5．复数函数

复数函数涉及复数的共轭（conj）、实部（real）、虚部（imag）和模（abs）的函数，在符号、数值计算中的使用方法相同。但需要注意的是，在符号运算中，MATLAB 7.0没有提供求相角的指令。

6．矩阵代数指令

在符号运算中，MATLAB 7.0提供的常用矩阵代数指令有diag、triu、tril、inv、det、rank、rref、null、colspace、poly、expm、eig和svd。它们的用法几乎与数值计算中的情况完全一样，只有svd稍微不同，后面将有详细的介绍。

8.3　任意精度数学计算

符号计算的一个非常显著的特点是由于计算过程中不会出现舍入误差，从而可以得到任意精度的数值解。如果希望计算结果精确，那么就可以牺牲计算时间和存储空间，用符号计算来获得足够高的计算精度。

在符号运算工具箱中有3种不同类型的算术运算：

·　数值类型：MATLAB 7.0的浮点算术运算；

·　有理数类型：Maple的精确符号计算；

·　VPA类型：Maple的任意精度算术运算。

这3种运算各有利弊，在计算时应根据计算精度、时间、存储控件的要求进行合理的选择。首先来看一下浮点运算和有理数运算的特点。下面是两种运算的例子：

由以上语句得到结果代码如下：

浮点运算是最快的运算，需要的计算机内存最小，但是结果不精确。MATLAB 7.0双精度数输出的数字位数由format命令控制，但它内部采用的是由计算机硬件提供的八位浮点的表示方法。而且，在上面的浮点运算中，存在三种舍入误差，第一是来自1/3的除法舍入误差；第二是来自将1/2加到1/3的结果上产生的舍入误差；第三是来自将二进制结果转化为十进制输出时的舍入误差。

而符号运算中的有理数算术运算，它所需要的时间和内存开销都是最大的。只要有足够的内存和足够长的计算时间，总能产生精确的结果。

一般符号计算的结果都是字符串，特别是一些符号计算结果从形式上看来是数值，但从变量类型上说，它们仍然是字符串，例如上面例子中的“5/6”实际上就是字符串，而非数值。要从精确解中获得任意精度的解，并改变默认精度，把任意精度符号解变成“真正的”数值解，就需要用到MATLAB 7.0提供的如下几个函数。

1．digits(d)

调用该函数后的近似解的精度变成d位有效数字。d的默认值是32位。

另外，调用digits命令（没参数）可以得到当前采用的数值计算的精度。

2．vpa(A,d)

求符号解A的近似解，该近似解的有效位数由参数d来指定。如果不指定d，则按照一个digits(d)指令设置的有效位数输出。

3．double(A)

把符号矩阵或任意精度表示的矩阵A转换成为双精度矩阵。

对于vpa函数的输入既可以是符号对象，也可以是数值对象，而其输出一定为符号对象。

【例8.6】指令使用演示。

下面的命令首先创建一个符号矩阵，然后分别将它转换成任意精度矩阵和双精度矩阵。

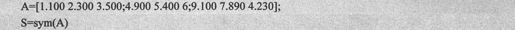
生成符号矩阵如下：

转换成有效位为4的任意精度矩阵如下：

转换成双精度型的矩阵如下：

8.4　符号表达式的化简和替换

从前面几节可以发现，符号计算所得的结果往往比较繁琐，非常不直观。为此，MATLAB7.0专门提供了对符号计算结果进行化简和替换的函数，诸如因式分解、同类项合并、符号表达式的展开、符号表达式的化简和通分等，它们都是表达式的恒等变换。

8.4.1　符号表达式的化简

MATLAB 7.0符号工具箱中提供了函数collect、expand、homer、factor、simplify和simple来实现符号表达式的化简。下面将分别介绍这些函数。

1．函数collect()

函数实现功能为将符号表达式中同类项合并，具体调用格式有两种：

·　R＝collect(S)：将表达式S中的相同次幂的项合并。其中S可以是一个表达式，也可以是一个符号矩阵。

·　R＝collect(S,v)：将表达式S中v的相同次幂的项进行合并。如果v没有指定，则缺省地将含有x的相同次幂的项进行合并。

下面是collect函数调用的一个例子：

【例8.7】

结果为：

2．函数expand()

函数实现功能为将表达式进行展开。它的调用格式为：

·　R＝expand(S)：它将表达式S中的各项进行展开，如果S包含函数，则利用恒等变形将它写成相应的和的形式。该函数多用于多项式，有时也用于三角函数、指数函数和对数函数。

下面是函数expand应用的两个例子：

【例8.8】多项式的展开示例：

得到结果代码如下：

【例8.9】三角函数的展开示例：

得到结果代码如下：

3．函数horner()

函数实现将符号表达式转换成嵌套形式。它的调用格式为：

·　R＝horner(S)：其中S是符号多项式矩阵，函数horner将其中每个多项式转换成它们的嵌套形式。

下面是函数horner应用的一个例子。

【例8.10】

示例代码设置如下：

得到结果代码如下：

4．函数factor()

函数实现将符号多项式进行因式分解。它的调用格式为：

·　factor(X)：如果X是一个多项式或多项式矩阵，系数是有理数，那么该函数将把X表示成系数为有理数的低阶多项式相乘的形式；如果X不能分解成有理多项式乘积的形式，则返回X本身。

下面是函数factor应用的一些例子：

【例8.11】

示例代码设置如下：

得到结果代码如下：

以下的指令将对如x^(n＋1)的多项式进行因式分解：

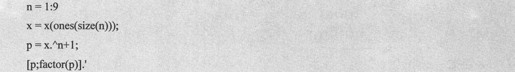
输出的矩阵中，每行的第一个元素为分解前的多项式，第二个元素为分解后的多项式。当n为偶数时，x^n＋1无法分解成有理多项式，所以返回它们自身。具体代码如下：

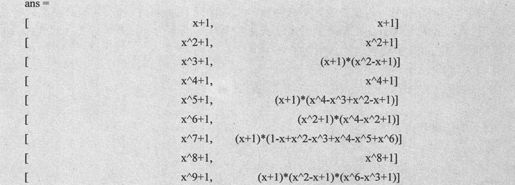
此外，函数factor还可以类似算术中质因数分解那样对正整数进行最简分解。当输入中的某个元素超过了16位，则必须先将该矩阵用函数sym定义成符号矩阵才能进行分解。这时，factor是对符号整数进行分解。事实上，具有对整数进行分解功能的是在特殊功能函数工具箱中的factor，它与这里讨论的符号工具箱中的factor同名。

下面的程序将对符号整数进行与上面类似的形式进行分解：

【例8.12】

示例代码设置如下：

得到的结果代码如下：

5．函数simplify()

根据一定的规则对表达式进行简化，它的调用格式为：

·　R＝simplify(S)：该函数是一个强有力的具有普遍意义的工具。它应用于包含和式、方根、分数的乘方、指数函数、对数函数、三角函数、Bessel函数以及超越函数等的表达式，并利用Maple化简规则对表达式进行简化。其中S可以是符号表达式矩阵。

下面是simplify函数应用的一个例子。

【例8.13】

得到的结果代码如下：

6．函数simple()

寻找一个符号表达式的最简形式。它的调用格式有：

·　r＝simple(S)：用几种不同的算术简化规则对符号表达式进行简化，返回使表达式S变得简短的形式。如果S使符号表达式矩阵，则返回使整个矩阵变成最短的形式，而不一定使每一项都最短；如果不给定输出参数r，该函数将显示所有使表达式S变短的简化形式，并返回其中最短的一个。

·　[r,how]＝simple(S)：不显示简化的中间结果，只显示寻找到的最短形式以及找到该形式所用的简化方法。返回值中，r是符号表达式，how是一个描述简化方法的字符串。

函数simple的目标是使表达式用最少的字符来表示。虽然并非表达式中的字符越少，表达式就越简洁，但采用这个标准往往能够得到满意的结果。为了达到这个最少字符的标准，simple函数综合使用了以下几个函数进行不同方式的化简：

·　用函数simplify对表达式进行化简；

·　用函数radsimp对包含根式的表达式进行化简；

·　用函数combine把表达式中以求和形式、乘积形式、幂形式出现的各项进行合并；

·　用函数collect合并同类项；

·　用函数factor实现因式分解；

·　用函数convert把一种形式转换成另一种形式。

函数simple比较这些函数的结果，最终把最少字符作为标准。下面是函数simple应用的一些例子，读者可以从中体会到该函数在进行化简时的强大功能。

【例8.14】

示例代码设置如下：

输出的结果代码如下：

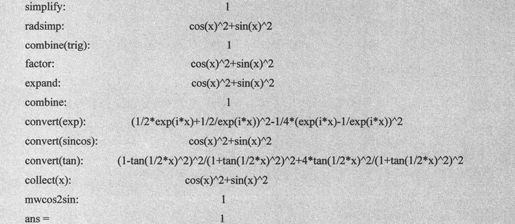
由于函数simple采用多种方法进行化简，所以它往往能够改善函数simplify给出的结果，特别值得一提的是，simple函数对于含有三角函数的表达式很有效。simple调用的很多函数都能把三角多项式进行化简。下面是用simple化简三角多项式的示例代码：

得到的结果代码如下：

8.4.2　符号表达式的替换

在MATLAB 7.0中，可以通过符号替换来使表达式的输出形式简化，从而可以得到比较简单的表达式。符号运算工具箱中提供了两个函数subexpr和subs，用于实现符号对象的替换。

1．函数subexpr

函数subexpr将表达式中重复出现的字符串用变量代替，它的调用格式如下：

·　[Y,SIGMA]＝subexpr(S,SIGMA)：指定用变量SIGMA的值（必须为符号对象）来代替符号表达式（可以是矩阵）中重复出现的字符串。替换后的结果由Y返回，被替换的字符串由SIGMA返回；

·　[Y,SIGMA]＝subexpr(S,'SIGMA')：这种形式和上一种形式的不同在于第二个输入参数是字符或字符串，它用来替换符号表达式中重复出现的字符串。其他参数同上面的形式相同。

下面是函数subexpr的一个例子：

【例8.15】

得到的结果代码如下：

所得到的结果非常繁琐，虽然用函数simple不能化简它，但是subexpr函数则可以更为简洁，代码如下所示：

得到的结果代码如下：

2．函数subs

函数subs可以用指定符号替换符号表达式中的某一特定符号。它的调用格式有：

·　R＝subs(S)：用工作空间中的变量值替代符号表达式S中的所有符号变量。如果没有指定某符号变量的值，则返回值中该符号变量不被替换；

·　R＝subs(S,New)：用新符号变量New替代原来符号表达式S中的默认变量。确定默认变量的规则与函数findsym的规则相同；

·　R＝subs(S,Old,New)：用新符号变量New替代原来符号表达式S中的变量Old。当New是数值形式的符号时，实际上用数值代替原来的符号来计算表达式的值，只是所得结果仍然是字符串形式。

下面是subs应用的一些例子。

【例8.16】

示例代码如下：

得到的结果代码如下：

除了本节介绍的一些简化和替换函数之外，符号数学工具箱还提供了一个将符号表达式显示起来比较美观的函数pretty。它在缺省情况下以每一行79个字符宽的格式表示符号表达式，如果表达式中有多次出现的字符串，它会用％n（n是整数）来代替它们。这是从Maple中继承而来的。下面举一个关于pretty的例子。

【例8.17】

示例代码如下：

得到的结果代码如下：

8.5　符号矩阵的计算

在进行符号运算时，很多方面在形式上同数值计算都是相同的，不必再去重新学习一套关于符号运算的新规则，这给MATLAB 7.0用户带来了极大的方便。这里要介绍的符号对象的矩阵运算在形式上与数值计算中的运算十分相似，读者很容易掌握。

8.5.1　基本代数运算

在MATLAB 7.0中，符号对象的代数运算和双精度运算从形式上看是一样的。由于MATLAB 7.0中采用了符号的重载，用于双精度数运算的运算符同样可以用于符号对象。

符号对象的加减法运算必须满足下列原则，如果两个对象都是符号矩阵，那么它们必须大小相等。当然，符号矩阵也可以和符号标量进行加减运算，运算按照数组运算法则进行。

【例8.18】符号矩阵的加减运算，示例代码设置如下：

得到的结果代码如下：

关于符号矩阵的乘法（包括幂）运算必须要求参与运算的矩阵符合矩阵相乘的规则，例如第一个矩阵的列数等于第二个矩阵的行数等。对于这些基本的操作，限于篇幅，这里就不再赘述了，读者可以按照数值计算的部分进行练习。

8.5.2　线性代数运算

符号对象的线性代数运算和双精度数的线性代数运算一样，读者可以参阅本书第2章的有关内容来了解有关线性代数运算的一些规则和注意事项。这里仅举一个例子进行说明。

在下面的例子中，先生成数值希尔伯特矩阵，然后再将它转换成符号矩阵，并对它进行各种线性代数运算。读者可以从中体会符号对象线性代数运算的特点。示例代码如下：

得到的结果代码如下：

在上面的运算中，矩阵求逆和求行列式都采用的是符号计算，得到的结果都是精确解。下面用指定精度来计算上面的各项，将符号计算和数值计算进行一下比较。设置代码如下：

得到一定精度的矩阵：

上面把矩阵的每个元素的值按照四舍五入法转换成为16位有效数字，这时再来求矩阵的逆，这些舍入误差就会被放大。按照数值计算理论，放大的倍数就是矩阵的条件数。希尔伯特矩阵是一个严重病态矩阵，它的条件数非常大（3阶矩阵的条件数大约为500）。所以，误差将变的很大，这可以通过下面的计算中看到。

求逆的结果代码如下：

可见，矩阵中的最后几位均为误差。下面再来看行列式的值：

行列式的值如下：

下面通过修改H(1,1)的值，将H变成奇异矩阵，并以它为例介绍奇异矩阵的特性：

得到H(1,1）的值如下：

再来求行列式，代码设置如下：

得到新的行列式的值如下：

再求出Z＝0的s值，将它赋予sol。

得到sol的值如下：

将sol替换s，得到奇异矩阵：

求新的符号矩阵的逆矩阵：

得到结果代码如下：

由于H为奇异矩阵，所以求H的逆时将会给出错误信息。必须指出的是，虽然矩阵H是奇异矩阵，当采用任意精度进行计算时，无论求H的行列式还是逆矩阵，得到的结果均不是0。这就是数值计算和符号计算的根本区别。

8.5.3　特征值分解

在MATLAB 7.0中，分别采用下面的函数来求符号方阵的特征值和特征向量：

·　E＝eig(A)：求符号方阵A的符号特征值E；

·　[v,E]＝eig(A)：返回方阵A的符号特征值E和相应的特征向量v。

与它们对应的任意精度计算的指令是E＝eig(vpa(A))和[v,E]＝eig(vpa(A))。对于上一节最后给出的矩阵H，由于它是奇异矩阵，肯定有一个特征值为0：

得到的特征值和特征向量分别如下：

生成的矩阵v和E中，v的每一列就是H的一个特征向量，相应的E的对角线元素就是H的特征值。

8.5.4　约当标准型

对矩阵进行相似变换时，会产生约当标准型（Jordan Canonical Form）。对于矩阵A，求它的约当标准型，也就是找一个非奇异矩阵V，使J＝V/A*V最接近对角矩阵，其中的V称为转换矩阵。

当矩阵对称且所有特征值均互异时，其约当标准型就是其特征值所组成的对角矩阵，相应的转换矩阵由特征向量按列组成。对于非对称或有重特征值的情形，约当标准型的对角元素由特征值组成，但对角线上面有非零元素。

MATLAB 7.0提供了函数jordan来求矩阵的约当标准形，它的调用格式有：

·　J＝jordan(A)：计算矩阵A的约当标准型。其中A可以是数值矩阵或符号矩阵；

·　[V,J]＝jordan(A)：除了计算矩阵A的约旦标准型J外，还返回相应的变换矩阵V。

需要特别注意的是，函数jordan对矩阵元素值的极微小变化均特别敏感，这使得采用数值方法计算约当标准型非常困难，矩阵A的值必须精确地知道它的元素是整数或有理式（例如，没有舍入误差）。对于任意精度矩阵是不提倡求其约当标准型的。例如下面的示例代码：

得到的结果代码如下：

8.5.5　奇异值分解

在符号数学工具箱中只有任意精度矩阵的奇异值分解才是可行的，其中一个重要原因就在于由符号计算产生的公式一般都太长、太复杂，而且没有太多的用处。用于对符号矩阵A进行奇异值分解的函数式svd，它的调用格式如下：

·　S＝svd(A)：给出符号矩阵奇异值对角矩阵，其计算精度由函数digits来指定；

·　[U,S,V]＝svd(A)：输出参数U和V是两个正交矩阵，它们满足关系式：A＝USV'。

下面考虑一个矩阵A，它的元素同时为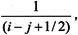其中i和j分别为矩阵的行号和列号，示例代码设置如下：

得到A矩阵为：

鉴于A中的每个元素都是有理形式，可以采用指定精度计算得到较精确的解。命令如下：

得到的结果代码如下：

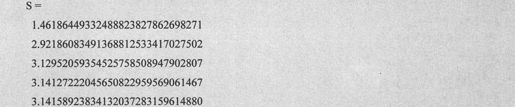
8.6　符号微积分

微积分运算在数学计算中的重要性是不言自明的，整个高等数学就是建立在微积分运算的基础上的。同时微积分运算也是后面解符号微分方程的必要知识准备。

在符号数学工具箱中提供了一些常用的函数来支持具有重要基础意义的微积分运算，涉及的方面主要包括微分、求极限、积分、级数求和和泰勒级数等。下面来具体介绍符号运算在微积分中的使用方法。

8.6.1　符号表达式的微分运算

1．diff函数

当创建了符号表达式后，就可以利用函数diff对它们进行微分运算。函数diff的调用格式有3种，它们的形式和作用分别如下：

·　diff(S,'v')：将符号“v”视作变量，对符号表达式或符号矩阵S求取微分；

·　diff(S,n)：将S中的默认变量进行n阶微分运算，其中默认变量可以用findsym函数确定，参数n必须是正整数；

·　diff(S,'v',n)：将符号“v”视作变量，对符号表达式或矩阵S进行n阶微分运算。

例如，我们首先建立一个符号表达式，然后取相应的微分，示例代码设置如下：

得到的结果代码如下：

再对符号表达式中的指定变量a求二阶微分：

得到的结果代码如下：

2．jacobian函数

微分运算也可以对列向量进行，所得的结果也是一个列向量。现在来考察笛卡尔坐标（x，y，z）和球坐标（r，θ，φ）的转换问题。坐标之间的转换关系为x＝r×cosθcosφ，y＝r×cosθsinφ和z＝r×sinθ。其中θ对应于仰角或纬度，而φ代表方位角或经度。在数学中，它们之间转换的矩阵为雅可比矩阵。用函数jacobian可以计算这个转换矩阵J，它的数学表达式为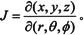可见求变换矩阵的本质还是求取微分。

函数jacobian的调用格式如下：

·　R＝jacobian(w,v)：其中w是一个符号列向量，v是指定进行变换的变量所组成的行向量。

笛卡尔坐标和球坐标之间转换雅可比矩阵J可以用如下的命令求得：

得到的结果代码如下：

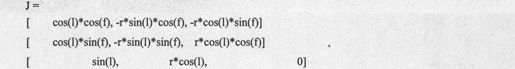
再来计算雅可比矩阵的行列式，并进行简化：

得到的结果代码如下：

注意：雅可比函数的第一个参数必须是列向量，第二个参数必须是行向量。此外，由于雅可比矩阵的行列式值一般是比较复杂的，我们可以对这些复杂的结果进行三角函数变换和简化，以便得到具有较为简便的形式。

8.6.2　符号表达式的极限

求微分的基本思想是当自变量趋近某个值时，求函数值的变化。“无穷逼近”是微积分的一个基本思想，求极限是非常普遍的。事实上，导数就是由极限给出的：

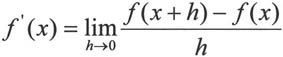
在MATLAB 7.0中，用函数limit来求表达式的极限。函数limit的调用格式如下：

·　limit(F,x,a)：求当x→a时，符号表达式F的极限；

·　limit(F,a)：符号表达式F采用默认自变量（可由函数findsym求得），该函数求F的自变量趋近于a时的极限值；

·　limit(F)：符号表达式F采用默认自变量，并以a＝0作为自变量的趋近值，从而求符号表达式F的极限值；

·　limit(F,x,a,'right')或limit(F,x,a,'left')：分别求取符号表达式F的左极限和右极限，即自变量从左边或右边趋近于a时的函数极限值。

例如，下面的命令分别计算sin函数的导数和幂函数的极限（指数函数）：

求得的结果代码如下：

求极限可以从两边趋近，从不同的方向趋近可能得到的结果也不相同。limit函数第4种调用方式提供了求单边极限的功能。比如，下面的3个表达式的值时不同的。需要注意的是，MATLAB 7.0对于没有定义的极限将返回NaN：

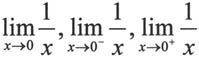
用下面的命令来验证这一结论：

得到的结果代码如下：

8.6.3　符号表达式的积分

数学中，积分和微分是一对互逆的运算。符号数学工具箱种提供了函数int来求符号表达式的积分，它的调用格式如下：

·　R＝int(S)：用缺省变量求符号表达式S的不定积分，缺省变量可用函数findsym确定；

·　R＝int(S,v)：用符号标量v作为变量求符号表达式S的不定积分值；

·　R＝int(S,a,b)：符号表达式采用缺省变量，该函数求缺省变量从a变到b时符号表达式S的定积分值。如果S是符号矩阵，那么积分将对各个元素进行分别进行，而且每个元素的变量也可以独立地由函数findsym来确定，a和b可以是符号或数值标量；

·　R＝int(S,v,a,b)：符号表达式采用符号标量v作为标量，求当v从a变到b时，符号表达式S的定积分值。其他参数和上一种调用方式相同。

例如，下面用各种调用方式求符号表达式和符号矩阵的积分值，首先是用缺省变量对符号表达式求积分。

得到的结果代码如下：

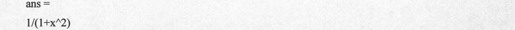
和微分运算比起来，积分的运算困难要大得多。当函数和积分不存在时，MATLAB 7.0将简单地返回原来的积分表达式。例如，下面的命令试图求贝赛尔函数的积分：

得到的结果代码如下：

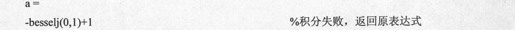
在符号数学工具箱中，常数是积分时一个比较敏感的问题。例如表达式e^-(kx)2，当k为实数时，该表达式的值永远为正；并且当x的值趋于正负无穷时，该表达式的值趋于0。但是Maple的内核并不把k²或x²看作正数，而只是简单地假定它们为符号，其值不定，没有丝毫的数学属性。用下面的命令计算该积分，将给出错误信息：

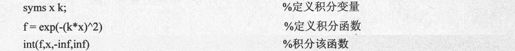
得到的结果代码如下：

从上面的结果我们发现，当k^2大于0的情况下，积分可以得到，而当其他情况下积分为无穷大。因此，在计算前，应当首先定义k为实变量，这样才能得到正确的结果：

得到的结果代码如下：

注意：上面的k既是MATLAB 7.0工作控件中的变量，同时也是Maple内核工作空间中的一个实变量，命令“clear k”只能从MATLAB 7.0的工作空间中删除符号对象k，但在Maple内核空间中还存在实变量k。可以利用“syms k unreal”命令从Maple内核空间中删除k。

8.6.4　级数的求和

函数symsum用于对符号表达式进行求和。该函数的调用格式如下：

·　r＝symsum(s,a,b)：求符号表达式s中默认变量从a变到b时的有限和；

·　r＝symsum(s,v,a,b)：求符号表达式s中变量v从a变到b时的有限和。

具体的示例代码如下：

得到的结果代码如下：

8.6.5　泰勒级数

函数taylor用来求符号表达式的泰勒级数展开式，该函数的调用格式如下：

·　r＝taylor(f)：f是符号表达式，其变量采用默认变量，该函数将返回f在变量等于0处作5阶泰勒展开时的展开式；

·　r＝taylor(f,n,v)：符号表达式f以符号标量v作为自变量，返回f的n-1阶麦克劳林级数（即在v＝0处作泰勒展开）展开式；

·　r＝taylor(f,n,v,a)：返回符号表达式f在v＝a处作n-1阶泰勒展开的展开式。

例如，下面的命令将返回函数的8阶泰勒展开式：

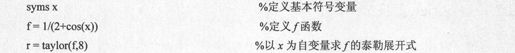
得到的结果代码如下：

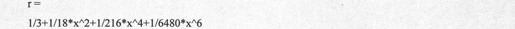
下面的命令将给出函数在x＝2处展开的前3个非零项：

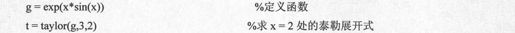
得到的结果代码如下：

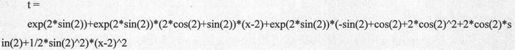
下面的命令将求出函数sin(x)*e-x的麦克劳林级数：

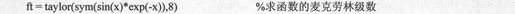
得到的结果代码如下：

8.7　符号积分变换

在数学中，为了把较复杂的运算转化为比较简单的运算，经常采用一种变换手段。例如数量的乘积或商可以通过对数学变换成对数的和或差，然后再取反对数即可求得原来数量的乘积或商。这一变换方法的目的就是把比较复杂的乘除运算通过对数变换转化为简单的加减运算。

所谓积分变换，就是通过积分运算，把一类函数A变换成另一类函数B，函数B一般是含有参量a的积分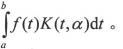这一变换的目的，就是把某函数类A中的函数f(t)通过积分运算变成另一类函数B中的函数F(a)。这里K(t,a)是一个确定的二元函数，叫做积分变换的核。当选取不同的积分区间与变换核时，就成为不同的积分变换。f(t)叫做原函数，F(a)叫做象函数。在一定条件下，原函数与象函数两者一一对应，成为一个积分变换对。变换时可逆，有原函数求象函数叫做正变换，反之则是逆变换。

积分变换的理论与方法，在自然科学与工程技术的各个领域中都有着极广泛的应用，成为不可缺少的运算工具。所有变换的使用，都会极大地简化计算，有的变换则为开创新的学科奠定了基础。

以下要介绍3种积分变换，即Fourier变换、Laplace变换与Z变换。

8.7.1　Fourier变换

时域中的f(t)与它在频域中的Fourier变换F(ω)之间存在如下关系：

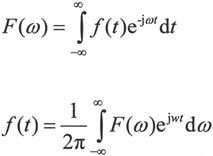
由计算机完成这种变换的途径有两条：一种是直接调用指令fourier和ifourier进行；另一种是根据上面的定义，利用积分指令int实现。下面只介绍fourier和ifourier的使用及相关注意事项。至于根据定义求变换，请读者自己完成。

·　Fw＝fourier(ft,t,w)：求时域函数ft的ourier变换Fw，ft是以t为自变量的时域函数，Fw是以圆频率w为自变量的频域函数；

·　ft＝ifourier(Fw,w,t)：求频域函数Fw的Fourier反变换，ft是以t为自变量的时域函数，Fw是以圆频率w为自变量的频域函数。

下面的示例代码将给出Fourier变换的具体实现：

得到的结果代码如下：

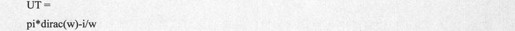
再来求Fourier反变换：

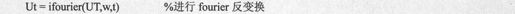
得到的结果代码如下：

同原先的时域函数相同。

注意：在MATLAB 7.0的符号数学工具箱中增加了dirac和heaviside两个函数，它们分别是单位脉冲函数和阶跃函数。在老版本的MATLAB中，如果需要调用这两个函数，则必须从Maple函数库中调用，因为原先的MATLAB本身没有这样的函数提供。

8.7.2　Laplace变换

Laplace变换和反变换的定义为：

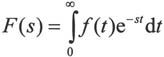
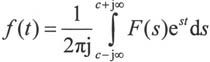
与Fourier变换相似，Laplace变换与反变换的实现也有两条途径。直接调用指令laplace和ilaplace进行，或者根据上面的定义，利用积分指令int实现。比较而言，直接使用laplace和ilaplace指令实现变换较为简洁。具体使用方法如下：

·　Fs＝laplace(ft,t,s)：求时域函数ft的Laplace变换Fs，ft是以t为自变量的时域函数，Fs是以复频率s为自变量的频域函数；

·　ft＝ilaplace(Fs,s,t)：求频域函数Fs的Laplace反变换ft，ft是以t为自变量的时域函数，Fs是以复频率s为自变量的频域函数。

下面的例子给出Laplace变换的具体实现：

求的Laplace变换。

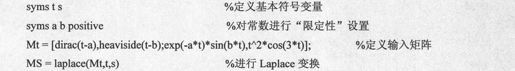
得到的结果代码如下：

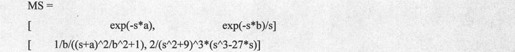
8.7.3　Z变换

一个离散因果序列的Z变换及其反变换定义为：

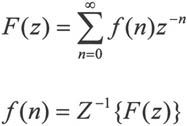
涉及Z反变换具体计算的方法，最常见的有3种，分别是幂级数展开法、部分分式展开法和围线积分法。MATLAB 7.0的符号数学工具箱中采用了围线积分法设计了求取Z反变换的iztrans指令，相应的数学表达式是具体的命令格式如下：

·　FZ＝ztrans(fn,n,z)：求时域函数fn的Z变换FZ, fn是以n为自变量的时域序列，FZ是以复频率z为自变量的频域函数；

·　fn＝iztrans(FZ,z,n)：求频域函数FZ的Z反变换fn, fn是以n为自变量的时域序列，FZ是以复频率z为自变量的频域函数。

下面的例子给出Laplace变换的具体实现：

下面的例子给出Laplace变换的具体实现：

求序列的Z变换，并用反变换验算。

示例代码如下：

得到的结果代码如下：

再来求序列f(n)的Z变换，示例代码如下：

得到的结果代码如下：

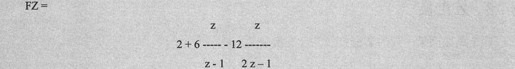
最后Z反变换，示例代码如下：

得到的结果代码如下：

说明：在输入函数的定义上，我们引入了一个函数charfcn，需要说明的是，这个函数是Maple V5中的表达式的指征函数（Characteristic function），它满足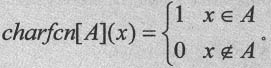

8.8　符号方程求解

从学习代数开始，我们就一直在探索关于方程的求解理论，从最初的代入消元法和加减消元法到数值计算中的牛顿迭代法、高斯消元法，一直到微分方程的求解理论，方程在数学中的重要性就包含在这么漫长的探索、深化过程中。MATLAB 7.0为符号方程的求解提供了强有力的支持。

符号方程根据其中涉及到的运算类别，可以分为代数方程和微分方程。其中代数方程只涉及到符号对象的代数运算，相对比较简单，它还可以细分为线性方程和非线性方程两类。前者往往可以很容易地求得所有解，但是对于后者来说，却经常容易丢掉一些解，这时就必须借助绘制函数图形，通过图形来判断方程解的个数。

微分方程的求解稍微复杂一些，它按照自变量的个数，可以分为常微分方程和偏微分方程。偏微分方程的求解在数学上相当复杂，而且理论体系也繁杂，用机器求解往往不能找到通行的方法，所以这里介绍用MATLAB 7.0求解常微分方程。

8.8.1　代数方程的求解

这里所讲的一般代数方程包括线性、非线性和超越方程等，求解指令是solve。当方程组不存在符号解时，若又无其他自由参数，则solve将给出数值解。该指令的使用格式包括以下几种：

·　g＝solve(eq)：其中eq可以是符号表达式或不带符号的字符串，该函数将求解方程eq＝0，其自变量采用默认变量，可以通过函数findsym来确定；

·　g＝solve(eq,var)：求解方程eq＝0，其自变量由参数var指定。其中eq和上一种调用方式相同。返回值g是由方程的所有解构成的列向量；

·　g＝solve(eq1,eq2,…,eqn)：求解由符号表达式或不带符号的字符串eq1，eq2，…，eqn组成的方程组。其中的自变量为整个方程组的默认变量，即将函数findsym作用于整个方程组时返回的变量；

·　g＝solve(eq1,eq2,…，eqn,var1,var2,…,varn)：求解由符号表达式或不带等号的字符串eq1，eq2，…，eqn组成的方程组。其自变量由输入参数var1，var2，…，varn指定。

对于上面的4种调用方式，输出的解有3种情况：

·　对于单个方程单个输出参数的情况，将返回由多个解构成的列向量；

·　对于有和方程数目相同的输出参数的情况，方程组的解将分别赋给每个输出参数，并按照字母表的顺序进行排列；

·　对于只有一个输出参数的方程组，方程组的解将以结构矩阵的形式赋给输出参数。

下面给出一个代数方程的求解过程：

求方程组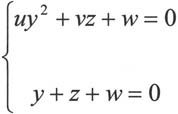关于y，z的解。

得到解如下：

注意：需要注意的是如果没有指定变量，findsym将把w，y依次作为自变量，最终的结果将与现在不同，读者可以自己尝试。

8.8.2　微分方程的求解

在前面已经讲过：从数值计算角度看，与初值问题求解相比，微分方程边值问题的求解显得复杂和困难。对于应用数学工具去求解实际问题的科研人员来说，此时，不妨通过符号计算指令进行求解尝试。因为，对于符号计算来说，不论是初值问题，还是边值问题，其求解微分方程的指令形式都相同，且相当简单。

当然，符号计算可能花费较多的计算机资源，可能得不到简单的解析解或封闭形式的解，甚至无法求解。既然没有万能的微分方程一般解法，那么：求解微分方程的符号法和数值法有很好的互补作用。

函数dsolve用来求常微分方程的符号解。在方程中，用大写字母D表示一次微分，D2、D3分别表示二次、三次微分运算。以此类推，符号D2y表示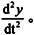函数dsolve把后面的字符当作因变量，并默认所有这些变量对符号t进行求导。函数dsolve的调用方式有：

·　r＝dsolve('eq1,eq2,…','cond1,cond2,…','v')：求由eq1，eq2，…指定的常微分方程的符号解。常微分方程以变量v作为自变量，参数cond1，cond2，…用于指定方程的边界条件或者初始条件。如果v不指定，将默认t为自变量；

·　r＝dsolve('eq1','eq2',…,'cond1','cond2',…,'v')：求由eq1，eq2，…指定的常微分方程的符号解。这些常微分方程都以v作为自变量。这些单独输入的方程的最大允许个数为12。其他参数与上一种调用方式相同。

微分方程的初始条件或边界条件都以变量v作为自变量，其形式为y(a)＝b或Dy(a)＝b，其中y是微分方程的因变量，a和b是常数。如果指定的初始条件和边界条件比方程中的因变量个数少，那么所得的解中将包含积分常数C1、C2等。

函数dsolve的输出结果同solve类似，既可以用和因变量个数相同数目的输出参数分别接收每个变量的解，也可以把方程的解写入一个结构数组中。

下面举两个常微分方程求解的例子：

求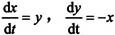的解。示例代码如下：

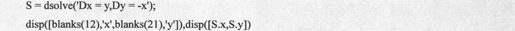
得到的结果代码如下：

求解两点边值问题：xy''－2y'＝x²，y(1)＝0，y(2)＝5。

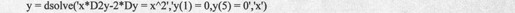
得到的结果代码如下：

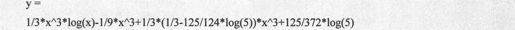
注意：在本例程中如果用数值解法，则比较复杂，有兴趣的读者可以自己尝试。

8.9　可视化数学分析界面

MATLAB 7.0的符号数学工具箱为符号函数可视化提供了一组简便易用的指令。本章着重介绍两个进行数学分析的可视化界面，即图示化符号函数计算器（由指令funtool引出）和泰勒级数逼近分析界面（由指令taylortool引出）。

8.9.1　图示化符号函数计算器

对于习惯使用计算器或者只是向作一些简单的符号运算与图形处理的读者，MATLAB 7.0提供的图示化符号函数计算器是一个较好的选择。该计算器功能虽简单，但操作方便，可视性强。

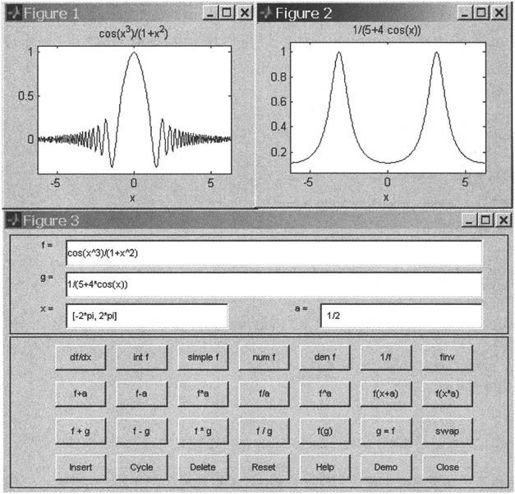
图8-1　图示化符号函数计算器界面

在如图8-1所示的图示化符号函数计算器是由2个图形窗口（Figure No.1和Figure No.2）与一个函数运算控制窗口（Figure No.3）3个独立窗口组成。在任何时候，两个图形窗口只有一个处于激活状态。函数运算控制窗口上的任何操作都只能对被激活的函数图形窗口起作用，即被激活的函数图像可随运算控制窗口的操作而作相应的变化。

（1）第1排按键只对f起作用，如求导、积分、简化、提取分子和分母、计算1/f以及求反函数。

（2）第2排按键处理函数f和常数a之间的加、减、乘、除等运算。

（3）第3排的前4个按键对两个函数f和g之间进行算术运算。第5个按键求复合函数，第6个按键的功能是把f函数传递给g，最后一个按键swap是实现f和g的互换。

（4）第4排按键用于对计算器自身进行操作。funtool计算器有一张函数列表fxlist。这7个按键的功能依次是：

·　Insert：把当前激活窗的函数写入列表；

·　Cycle：依次循环显示fxlist中的函数；

·　Delete：从fxlist列表中删除激活窗的函数；

·　Reset：使计算器恢复到初始调用状态；

·　Help：获得关于界面的在线提示说明；

·　Demo：自动演示。

8.9.2　泰勒级数逼近分析器

在MATLAB 7.0指令窗口中运行以下指令，将引出如图8-2所示的泰勒逼近分析界面。

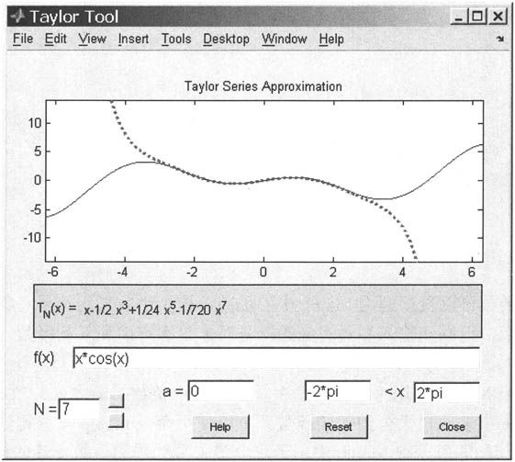
图8-2　泰勒级数逼近分析界面

·　该界面用于观察函数f(x)在给定区间上被N阶泰勒多项式T_N(x)逼近的情况；

·　函数f(x)的输入方式有两种，直接由指令taylortool(fx)引入，或者在界面的f(x)栏中直接键入表达式，然后回车输入；

·　界面中N被缺省地设置为7，可以用其右侧的按键改变阶次，也可以直接写入阶次；

·　界面上的a是级数的展开点，缺省值为0；

·　函数的观察区被缺省地设置为（-2π，2π）。

8.10　Maple接口

相对于Maple中的2000多条符号计算指令而言，前面介绍的函数只是其中的一小部分。为了在MATLAB 7.0中进一步利用Maple的符号计算能力，要求用户必须对Maple有较深的理解。符号数学工具箱为此提供了两个函数，即sym和maple。

sym和maple这两个指令可以实现对Maple绝大多数符号计算指令的调用，利用它们可以大大扩充MATLAB 7.0的符号计算功能。下面将通过示例分别介绍两个指令的使用。

8.10.1　利用sym函数调用Maple函数

例如，通过函数sym来调用Maple的阶乘函数k！，代码设置如下：

这相当于定义了一个可以用来计算正整数阶乘的符号函数。利用它来计算一下阶乘7！和n！，相应的命令如下：

得到的结果代码如下：

8.10.2　利用maple函数调用Maple函数

采用maple函数可以直接调用Maple中的函数。这个函数采用符号对象、字符串和双精度数作为输入参数，返回和输入参数对应的符号对象、字符串和双精度数。也可以利用函数maple来测试用户自己编写的符号数学程序。

假定要写一个M文件，用来计算两个多项式和两个整数的最大公约数。为此，首先要知道怎样调用Maple中求取最大公约数的函数。可以使用命令mhelp来获得这方面的信息。输入命令“mhelp gcd”即可获得Maple中用于求取最大公约数的函数gcd的相关信息。

当已经知道了如何调用函数gcd后，就可以编写一个简单的M文件gcd.m来调用这个Maple函数，从而轻松地求得两个多项式或整数的最大公约数。M文件的内容如下：

这样就可以简单地调用该文件，并利用Maple函数求最大公约数。示例代码如下：

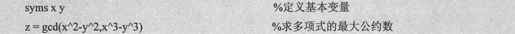
得到的结果代码如下：

可见，利用maple函数直接调用Maple中的函数，将大大地扩充MATLAB 7.0的符号计算功能。如果读者有什么特殊的符号计算要求，而不能由MATLAB 7.0来完成，不妨通过调用Maple函数来解决。