第3章　数学运算

本章将介绍MATLAB 7.0中与数学运算有关的函数和概念。在MATLAB 7.0中一切数据均以矩阵的形式出现，它的数学运算则包括两种：一种是针对整个矩阵的数学运算，称之为矩阵运算，例如求矩阵的行列式的函数det()；另一种是针对矩阵的每一个元素进行运算的函数，称之为矩阵元素的运算，例如求矩阵每一元素的正弦值的函数sin()。

本章3.1小节中将介绍矩阵运算函数，包括矩阵分析、线性方程组、矩阵分解、矩阵的特征值和特征向量，以及非线性矩阵运算。3.2小节将介绍矩阵元素的运算函数，包括三角函数、指数对数函数、复数函数和截断求余函数。3.3小节介绍特殊数学函数，这些函数应该属于矩阵元素的运算，特殊数学函数包括特殊函数、数论函数和坐标变换函数。由于特殊数学函数在使用和应用场合与3.2小节介绍的函数差异较大，故单独做一小节介绍。

3.1　矩阵运算

矩阵运算是线性代数中极其重要的部分。MATLAB 7.0可以支持很多线性代数中定义的操作。MATLAB 7.0强大的矩阵运算能力使其成为优秀数值计算软件。

本小节将介绍与矩阵运算相关的内容，包括矩阵分析、线性方程组求解、特征值求解和奇异值等。

3.1.1　矩阵分析

MATLAB 7.0提供的矩阵分析函数如表3-1所示。

表3-1　　　　　　矩阵分析函数

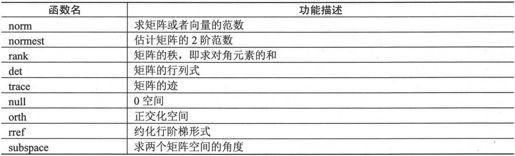
1．向量和矩阵的范数运算

对于线性空间中的一个向量x＝｛x₁，x₂，…x_n｝，如果存在一个函数ρ（x）满足以下3个条件：

（1）ρ（x）＞0，且ρ（x）＝0的充要条件为x＝0；

（2）ρ（ax）＝｜a｜ρ（x），其中a为任意标量；

（3）对向量x和y，有ρ（x＋y）≤ρ（x）＋ρ（y）。

称ρ（x）为向量x的范数，一般记为‖x‖。范数的形式多种多样，下面式子中定义的范数操作就满足以上3个条件：

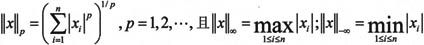
上式定义的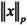称为p阶范数，其中最有用的是1、2和∞阶范数。

矩阵的范数是基于向量的范数定义的，其定义式如下：

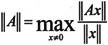
与向量的范数一样，矩阵的范数最常用的也是1、2和∞阶范数。它们的定义如下：

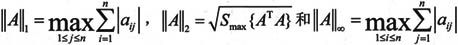
在上式中S（A）为矩阵A的特征值，而S_max｛A^TA｝则为A矩阵的最大奇异值的平方。

在MATLAB 7.0中，求向量范数的函数具体用法如下：

·　N＝norm(x,p)　对任意大于1的p值，返回向量x的p阶范数；

·　N＝norm(x)　　返回向量的2阶范数，相当于N＝norm(x,2)；

·　N＝norm(x,inf)　返回向量的∞阶范数，相当于N＝max(abs(x))；

·　N＝norm(x,-inf)　返回向量的-∞阶范数，相当于N＝min(abs(x))。

在MATLAB 7.0中，求矩阵范数的函数具体用法如下：

·　N＝norm(A)　　计算矩阵的2阶范数，也就是最大奇异值；

·　N＝norm(A,p)　根据参数p的值不同，求不同阶的范数值。当p＝1时，计算矩阵A的1阶范数，相当于max(sum(abs(A)))。当p＝2时，计算矩阵A的2阶范数，相当于norm(A)。p＝inf时，计算矩阵A的∞阶范数，相当于max(sum(abs(A')))。当p＝'pro'时，计算矩阵A的F范数（Frobenius范数），相当于sqrt(sum(diag(A'*A)))。

例如求向量x的2阶范数，具体代码如下：

由上述语句得到具体代码如下：

例如求单位矩阵的1阶范数，具体代码如下：

由上述语句得到具体代码如下：

当矩阵维数比较大时会导致计算矩阵范数的时间比较长，并且当一个近似的范数值满足要求时，可以考虑使用函数normest()来估计2阶范数值。函数normest()最初开发时是为了提供给稀疏矩阵使用的，同时它也能接受满矩阵的输入，一般在满矩阵维数比较大时使用。

函数normest()的用法如下：

·　normest(S)　估计矩阵S的2阶范数值，默认允许的相对误差为1e-6；

·　normest(S,tol)　使用tol作为允许的相对误差。

例如，首先用函数生成一个1000×1000的柯西矩阵W，该柯西矩阵满足条件W_ij＝1／(x_i＋y_j)，其中x_i!＝x_j，y_j!＝y_j（当i!＝j），然后对该矩阵W求其2阶范数，最后对比函数norm()和normest()的效果，具体代码如下：

由上述语句得到如下代码：

由上述示例可以看出，函数norm()计算出的范数精确值为2.2469，耗时5.7660s，而函数normest()计算出的范数值也为2.2469，但耗时为0.1410s。这就说明了，采用函数normest()计算范数可以大大提高计算速度。

2．矩阵的秩

矩阵A中线性无关的列向量个数称为列秩，线性无关的行向量个数称为行秩。可以证明矩阵的列秩与行秩是相等的。矩阵求秩的方法很多，其中有些算法是稳定的，有些算法是不稳定的。MATLAB 7.0中用函数rank()来计算矩阵的秩，所采用的算法是基于矩阵奇异值分解基础上的，具体代码如下：

这种算法是最耗时，同时也是最稳定的。

函数rank()的用法如下：

·　rank(A)　　　用默认允许误差计算矩阵的秩；

·　rank(A,tol)　　给定允许误差计算矩阵的秩，tol＝max(size(A))*eps(norm(A))。

例如，求6阶单位矩阵的秩，具体代码如下：

由上述语句得到如下代码：

3．矩阵的行列式

矩阵A＝{a_ij}_n×n的行列式定义如下：

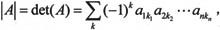其中k₁，k₂，…，k_n是将序列1，2，…，n交换k次所得的序列。

在MATLAB 7.0中用函数det()来计算矩阵的行列式。

例如，计算矩阵A＝[1 2 3;4 5 6;7 8 9]的行列式，如下：

由上述语句得到如下代码：

矩阵A的行列式恰好为0。

线性代数中定义行列式为0的矩阵为奇异矩阵。但是一般不能使用语句abs(det(A))<＝ɛ来判断矩阵A的奇异性，因为不容易选择合适的允许误差ɛ来满足要求。MATLAB 7.0提供函数cond()可以用来判定矩阵的奇异性。

4．矩阵的迹

矩阵的迹定义为矩阵对角元素之和。在MATLAB 7.0中用函数trace()来计算矩阵的迹。

例如，求矩阵A＝[1 2 3;4 5 6;7 8 9]的迹，如下：

由上述语句得到代码如下：

5．矩阵的化零矩阵

如果对于非满秩矩阵A，若有矩阵Z使得AZ的元素都为0，且矩阵Z为一个正交矩阵(Z'Z＝I)，则称矩阵Z为矩阵A的化零矩阵。MATLAB 7.0中提供了求化零矩阵的函数null()，用法如下：

·　Z＝null(A)　　返回矩阵A的一个化零矩阵，如果化零矩阵不存在则返回空矩阵；

·　Z＝null(A,'r')　返回有理数形式的化零矩阵。

例如，求矩阵A＝[1 2 3;1 2 3;4 5 6]的化零矩阵，具体代码设置如下：

由上述语句得到代码如下：

如果要求矩阵A的有理数形式的化零矩阵，具体代码设置如下：

由上述语句得到代码如下：

6．矩阵的正交空间

矩阵A的正交空间Q具有Q'*Q=I的性质，并且Q的列矢量构成的线性空间与矩阵A的列矢量构成的线性空间相同，且正交空间Q与矩阵A具有相同的秩。MATLAB 7.0中提供了函数orth()来求正交空间Q。

·　Q＝orth(A)，返回矩阵A的正交空间Q

例如，求出矩阵A的正交空间Q，并比较Q和A的秩，具体代码如下：

由上述语句得到代码如下输出：

7．矩阵的约化行阶梯形式

矩阵的约化行阶梯形式是高斯-约旦消去法解线性方程组的结果，其形式为：

MATLAB 7.0中提供了函数rref()来求矩阵的约化行阶梯形式，其用法如下：

·　R＝rref(A)，返回矩阵A的约化行阶梯形式R。

·　[R,jb]＝rref(A)，返回矩阵A的约化行阶梯形式R，同时返回1×r的向量jb使r为矩阵A的秩；A(:,jb)是矩阵A的列矢量构成的线性空间；R(1:r,jb)是r×r的单位矩阵。

·　[R,jb]＝rref(A,tol)，以tol作为误差容限计算矩阵A的秩。

例如，求出矩阵A的约化行阶梯形式，并比较Q和A的秩，具体代码设置如下：

由上述语句得到如下代码：

8．矩阵空间之间的夹角

矩阵空间之间的夹角代表两个矩阵线性相关的程度，如果夹角很小，它们之间线性相关度就很高，反之，它们之间线性相关度就不大。在MATLAB 7.0中用函数subspace()来实现求矩阵空间之间的夹角，其调用格式如下。

·　theta＝subspace(A,B)，返回矩阵A和矩阵B之间的夹角。

例如，求矩阵A和B之间的夹角，代码如下：

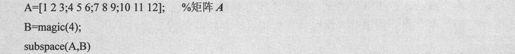
上述语句得到结果如下：

该结果表明矩阵A和矩阵B的线性相关度很低。

3.1.2　线性方程组

1．线性方程组的问题

在工程计算中，一个重要的问题是线性方程组的求解。在矩阵表示法中，上述问题可以表述为给定两个矩阵A和B，是否存在惟一的解X使得

AX＝B或XA＝B。

例如，求解方程3x＝6就可以将矩阵A和B看成是标量的一种情况，最后得出该方程的解为x＝6／3＝2。

尽管在标准的数学中并没有矩阵除法的概念，但MATLAB 7.0采用了与解标量方程中类似的约定，用除号来表示求解线性方程的解。MATLAB 7.0采用第2章介绍过的运算符斜杠'/'和运算符反斜杠'\'来表示求线性方程的解，其具体含义如下：

·　X＝A\B　　　表示求矩阵方程AX＝B的解；

·　X＝B/A　　　表示求矩阵方程XA＝B的解。

对于X＝A\B，要求矩阵A和矩阵B有相同的行数，X和B有相同的列数，X的行数等于矩阵A的列数。X＝B\A行和列的性质则与之相反。

在实际情况中，形式AX＝B的线性方程组比形式XA＝B的线性方程组要常见得多。因此反斜杠'\'用得更多。本小节的内容也主要针对反斜杠'\'除法进行介绍。斜杠'/'除法的性质可以由恒等变换式得到(B/A)'＝(A'\B')。

系数矩阵A不一定要求是方阵，矩阵A可以是m×n的矩阵，有如下3种情况：

·　m＝n恰定方程组，MATLAB 7.0会寻求精确解；

·　m＞n超定方程组，MATLAB 7.0会寻求最小二乘解；

·　m＜n欠定方程组，MATLAB 7.0会寻求基本解，该解最多有m个非零元素。

值得注意的是用MATLAB 7.0求解这种问题时，并不采用计算矩阵的逆的方法。针对不同的情况，MATLAB 7.0会采用不同的算法来解线性方程组。

2．线性方程组的一般解

线性方程组AX＝B的一般解给出了满足AX＝B的所有解。线性方程组的一般解可以通过下面的步骤得到。

·　解相应的齐次方程组AX＝O，求得基础解。可以使用函数null()来得到基础解。语句null(A)返回齐次方程组AX＝O的一个基础解，其他基础解与null(A)是线性关系。

·　求非齐次线性方程组AX＝B，得到一个特殊解。

·　非齐次线性方程组AX＝B的一般解等于基础解的线性组合加上特殊解。

在后面的章节将介绍求非齐次线性方程组AX＝B特殊解的方法。

3．恰定方程组的求解

恰定方程组是方程的个数与未知量个数相同的方程组。恰定方程组中矩阵A是一个方阵，矩阵B可能是一个方阵或者是一个列向量。

如果恰定方程组是非奇异的，则语句A\B给出了恰定方程组的精确解，该精确解与矩阵B的维数大小一样。具体代码设置如下：

由上述语句得到如下代码：

可以验证A*X精确地等于矩阵B。

如果恰定方程组是奇异的，则该方程的解不存在或者不惟一。执行语句A\B时，如果发现A是接近奇异的，MATLAB 7.0将给出警告信息；如果发现A是严格奇异的，MATLAB 7.0一方面给出警告信息，另一方面给出结果为inf。

一个奇异的恰定方程组如果解存在，则可以用矩阵A的伪逆矩阵pinv(A)来得到方程的一个解，其解为pinv(A)*B。例如有矩阵A＝[1 3 7;-1 4 4;1 10 18]，其行列式为0，可以通过如下代码验证：

由上述语句得到如下代码：

下面求解AX＝B，其中B＝[5;2;12]，具体代码如下：

由上述语句得到如下代码：

下面计算A*X，具体代码如下：

由上述语句得到如下代码：

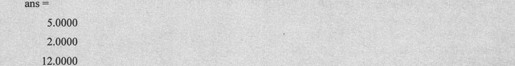
可以验证A*X精确等于B。

如果一个奇异的恰定方程组的精确解不存在，则式子pinv(A)B返回的是均方根值最小的解。例如B＝[3;6;0]，这时方程组无精确解，AX不等于B。若执行如下语句：

由上述语句得到如下代码：

可以发现，A*X并不等于B。

4．超定线性方程组的求解

超定线性方程组是方程的个数大于未知量个数的方程组。当进行实验数据拟合时，经常会碰到解超定线性方程组问题。下面举一个例子，设有两组如表3-2所示的观测数据x和y。若希望采用y＝c1x＋c2x²的模型来拟合这两组数据。该问题中共有11个方程，2个未知数，必须用最小二乘法来拟合来求解c1和c2。

表3-2　　　　　　观测数据

下面把该线性方程组问题用矩阵形式来表达，从而方便MATLAB 7.0计算。首先把x和y用列向量来表示，具体代码如下：

然后构造系数矩阵A，具体代码如下：

此时方程组可以写成：A*［c1 c2］'＝y，然后用反斜杠'＼'来求系数c1和c2，具体代码如下：

由上述语句得到如下代码：

最后，拟合得到y＝0.242x＋1.5407x²。具体代码如下：

由上述语句得到如图3-1所示的拟合结果和原始数据的对比图。

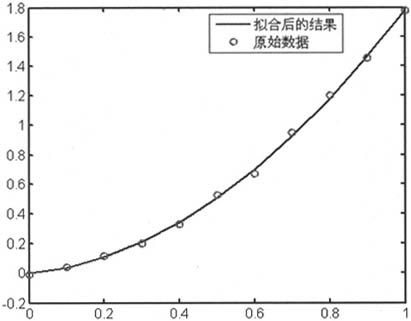
图3-1　拟合结果和原始数据对比

由图3-1可见，虽然拟合得到的结果与原始数据并不严格重合，但其差别比原始数据的测量误差要小。

5．欠定线性方程组的求解

欠定线性方程组是方程组的未知量个数多于方程个数的问题。这类问题的解不是惟一的。MATLAB 7.0将寻求一个基本解，该解至多有m个非零元素，然而，这些解往往也不是惟一的，MATLAB 7.0采用的是列主元QR分解算法来得到特解的。

例如，求一个欠定线性方程组的解，具体代码如下：

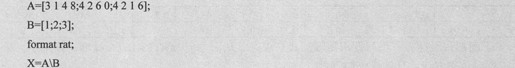
由上述语句得到如下代码：

因为本例中矩阵大小为3×4，所以解中共有3个非零元素。要得到该方程的通解还必须求方程的基本解，具体代码如下：

由上述语句得到如下代码：

该方程的通解可以表示为X_通解＝X＋Z*q，其中q为任意向量，表示可以对基本解进行线性组合。

3.1.3　矩阵分解

矩阵分解是把一个矩阵分解成几个“较简单”的矩阵连乘积的形式。无论在理论上还是工程应用上，矩阵分解都是十分重要的。本节将介绍几种矩阵分解的方法，相关函数如表3-3所示。

表3-3　　　　　矩阵分解函数

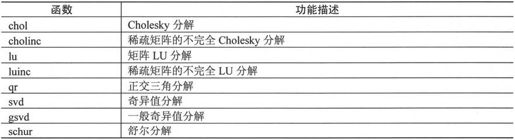
在MATLAB 7.0中，线性方程组的求解主要基于3种基本的矩阵分解，即对称正定矩阵的Cholesky分解、一般方阵的高斯消去法和矩形矩阵的正交分解。这3种分解分别通过函数chol()、lu()和qr()实现。这3种分解都使用了三角矩阵的概念。若矩阵的所有对角线以下的元素为0，则称为上三角矩阵；若矩阵的所有对角线以上的元素为0，则称为下三角矩阵。

本小节将具体介绍表3-3列出的5种分解方法。

1．对称正定矩阵的Cholesky分解

Cholesky分解是把一个对称正定矩阵A表示为一个上三角矩阵R与其转置的乘积，示例如下：

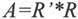
然而，并不是所有的对称矩阵都可以进行Cholesky分解。能进行Cholesky分解的矩阵必须是正定的，即矩阵的所有对角元素必须是正的，同时矩阵的非对角元素不会太大。矩阵i＝pascal(4)就是满足以上条件的矩阵，其值为：

Cholesky分解在MATLAB 7.0中用函数chol()来实现，其调用方式如下。

·　R＝chol(X)，其中X为对称正定矩阵，R是上三角矩阵，使得X＝R'*R。如果X是非正定的，结果将返回出错信息。

·　[R,p]＝chol(X)，返回两个参数，并且不会返回出错信息。当X是正定矩阵时，返回的上三角矩阵R满足X＝R'R，且p＝0；当X是非正定矩阵时，返回值p是正整数，R是上三角矩阵，其阶数为p－1，且满足X(1:p－1,1:p－1)＝R'R。

考虑线性方程组AX＝B，其中A可以做Cholesky分解，使得A＝R'R，这样线性方程组就可以改写成R'R*X＝B，由于左除算符'＼'可以快速处理三角矩阵，因此得出：

如果A是n×n的方阵，chol(A)的计算复杂度是O(n³)，而左除算符'＼'的计算复杂度只有O(n²)。

例如，分解pascal(4)矩阵，具体代码如下：

由上述语句得到如下代码：

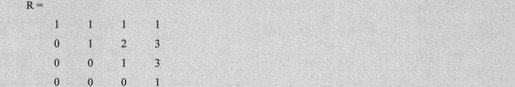
对于稀疏矩阵，MATLAB 7.0提供函数cholinc()来做不完全Cholesky分解。函数cholinc()的另一个优点是它可用于计算实半正定矩阵。函数cholinc()的调用格式如下。

·　R＝cholinc(X,DROPTOL)，其中X和R的含义与函数chol()中的变量相同，DROPTOL为不完全Cholesky分解的丢失容限。当DROPTOL设为0时，退化为完全Cholesky分解。

·　R＝cholinc(X,OPTS)，其中OPTS为结构体，它有3个属性，即DROPTOL、MICHOL和RDIAG。DROPTOL为不完全Cholesky分解的丢失容限；MICHOL为1时采用改进算法的不完全Cholesky分解，否则不采用改进算法；RDIAG为1时R的对角元素中的零值替换成为DROPTOL的平方根，RDIAG为0时不做此替换。

·　R＝cholinc(X,'O')，完全Cholesky分解。

·　[R,p]＝cholinc(X,'O')，返回两个参数，并且不会返回出错信息。当X是正定矩阵时，返回的上三角矩阵R满足X＝R'R，且p＝0；当X是非正定矩阵时，返回值p是正整数，R是上三角矩阵，其阶数为p－1，且满足X(1:p－1,1:p－1)＝R'R。

·　R＝cholinc(X,'inf')，采用Cholesky-Infinity分解。Cholesky-Infinity分解是基于Cholesky分解的，但它可以处理实半正定矩阵。

例如，对非正定矩阵进行chol分解，具体代码如下：

由上述语句得到错误信息如下：

但如果采用Cholesky-Infinity分解则不会出错，具体代码如下：

由上述语句得到如下代码：

其中，Rinf'*Rinf并不等于矩阵S。

2．一般方阵的高斯消去法

高斯消去法又称LU分解，它可以将任意一个方阵A分解为一个“心理”下三角矩阵L和一个上三角矩阵U的乘积，即A＝LU。“心理”下三角矩阵定义为下三角矩阵与置换矩阵的乘积。

LU分解在MATLAB 7.0中用函数lu()来实现，其调用方式如下。

·　[L,U]＝lu(X)，X为一个方阵，L为“心理”下三角矩阵，U为上三角矩阵，满足关系X＝L*U。

·　[L,U,P]＝lu(X)，X为一个方阵，L为下三角矩阵，U为上三角矩阵，P为置换矩阵，满足关系PX＝LU。

·　Y＝lu(X)，X为一个方阵。把上三角矩阵和下三角矩阵合并在矩阵Y中给出，矩阵Y的对角元素为上三角矩阵的对角元素，也即Y＝L＋U－I。置换矩阵P的信息丢失。

考虑线性方程组AX＝B，其中，对矩阵A可以做LU分解，使得A＝LU，这样线性方程组就可以改写成LU*X＝B，由于左除算符'＼'可以快速处理三角矩阵，因此可以快速解出：

矩阵的行列式的值和矩阵的逆也可以利用LU分解来计算，示例如下：

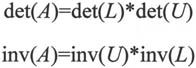
例如，做矩阵的LU分解，具体代码如下：

由上述语句得到如下代码：

对于稀疏矩阵，MATLAB 7.0提供了函数luinc()来做不完全LU分解，其调用格式如下。

·　[LU＝luinc(X,DROPTOL)，其中X、L和U的含义与函数lu()中的变量相同，DROPTOL为不完全LU分解的丢失容限。当DROPTOL设为0时，退化为完全LU分解。

·　[LU]＝luinc(X,OPTS)，其中OPTS为结构体，它有4个属性，即DROPTOL、MICHOL、RDIAG和THRESH。DROPTOL为不完全LU分解的丢失容限；MICHOL为1时采用改进算法的不完全LU分解，否则不采用改进算法；RDIAG为1时，R的对角元素中的零值替换成为DROPTOL的平方根，为0时不做此替换；THRESH是绕对角线旋转因子，其值范围是[0，1]，当THRESH为0时强制绕对角线旋转，THRESH的默认值是1。

·　[L,U,P]＝luinc(X,'0')，0级不完全LU分解。

·　[L,U]＝luinc(X,'0')，0级不完全LU分解。

·　Y＝luinc(X,'0')，0级完全LU分解。

例如，计算一个稀疏矩阵的不完全分解，并观察其非零元素的个数，具体代码如下：

由上述代码得到如图3-2所示的结果。由函数luinc()得到上三角矩阵U和下三角矩阵L，并且PS与LU有相似的稀疏结构。

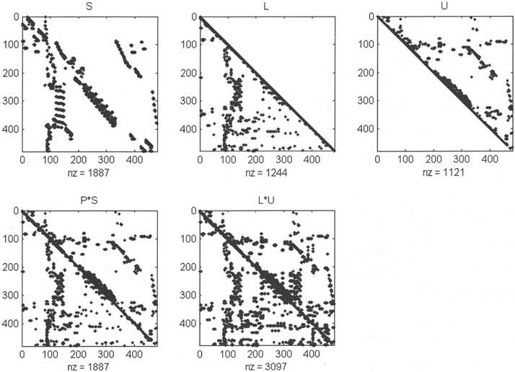
图3-2　不完全LU分解结果

3．矩形矩阵的正交分解

矩形矩阵的正交分解又称QR分解。QR分解把一个m×n的矩阵A分解为一个正交矩阵Q和一个上三角矩阵R的乘积，即A＝Q*R。

在MATLAB 7.0中QR分解由函数qr()来实现，下面介绍QR分解的调用方式。

·　[Q,R]＝qr(A)，其中矩阵R为与矩阵A具有相同大小的上三角矩阵，Q为正交矩阵。它们满足A＝Q*R。该调用方式适用于满矩阵和稀疏矩阵。

·　[Q,R]＝qr(A,0)，为“经济”方式的QR分解。设矩阵A是一个m×n的矩阵，若m＞n，则只计算矩阵Q的前n列元素，R为n×n的矩阵；若m＜＝n，则与[Q,R]＝qr(A)效果一致。该调用方式适用于满矩阵和稀疏矩阵。

·　[Q,R,E]＝qr(A)，R是上三角矩阵，Q为正交矩阵，E为置换矩阵。它们满足AE＝QR，程序选择一个合适的矩阵E使得abs(diag(R))是降序排列的。该调用方式适用于满矩阵。

·　[Q,R,E]＝qr(A,0)，“经济”方式的QR分解，其中E是一个置换矢量。它们满足A(:,E)＝Q*R。该调用方式适用于满矩阵。

·　R＝qr(A)，返回上三角矩阵R，这里R＝chol(A'*A)。该调用方式适用于稀疏矩阵。

·　R＝qr(A,0)，以“经济”方式返回上三角矩阵R。

·　[C,R]＝qr(A,B)，其中矩阵B必须与矩阵A具有相同的行数，矩阵R是上三角矩阵，C＝Q'*B。

例如，通过QR分解分析矩阵的秩，具体代码如下：

由上述语句得到如下代码：

矩阵R的第三行和第四行的元素为0，可以看出矩阵R不满秩，从而得到矩阵A的秩为2。该结果与用函数rank()得到的结果一致。

4．奇异值分解

奇异值分解在矩阵分析中占有极其重要的地位，即对于m×n的矩阵A，若存在m×m的酉矩阵U和n×n的酉矩阵V，使得A＝U∑V'，其中∑为一个m×n的非负对角矩阵，并且其对角元素的值按降序排列，则式子A＝U∑V'即为矩阵A的奇异值分解，U、∑和V称为矩阵A的奇异值分解的三对组。

在MATLAB 7.0中奇异值分解由函数svd()来实现，其调用方式如下。

·　[U,S,V]＝svd(X)，奇异值分解。

·　[U,S,V]＝svd(X,0)，“经济”方式的奇异值分解。设矩阵X的大小为m×n，若m＞n，则只计算U的前n列元素，S为n×n的矩阵；若m＜＝n，则与[U,S,V]＝svd(X)效果一致。

·　[U,S,V]＝svd(X,'econ')，设矩阵X的大小为m×n，若m＞＝n，则与[U,S,V]＝svd(X,0)效果一致，若m＜n，则只计算V的前m列元素，S为m×m的矩阵。

·　s＝svd(X)，返回包含所有奇异值的矢量。

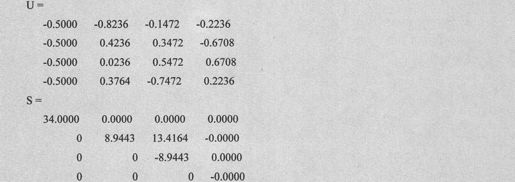
例如，把矩阵A分解为奇异值的三对组，具体代码如下：

由上述语句得到如下代码：

如果采用“经济”方式来求奇异值，具体代码如下：

由上述语句得到如下代码：

由上面的语句看出用“经济”方式得到的矩阵尺寸更小。

MATLAB 7.0还支持做一般奇异值分解运算。MATLAB 7.0中用函数gsvd()来进行一般奇异值分解，其基本调用格式如下：

·　[U,V,X,C,S]＝gsvd(A,B)，其中矩阵A和矩阵B必须拥有相同的列数，U和V是酉矩阵，X一般是一个方阵，C和S是非负对角矩阵。它们之间的关系如下：A＝UCX',B＝VSX'，CC＋S'S＝I。若A和B分别是m×p和n×p的矩阵，则U是m×m的矩阵，V是n×n的矩阵，X是q×q的方阵，其中q＝min(m＋n,p)。

·　sigma＝gsvd(A,B)，返回包含所有一般奇异值的矢量，它等于qrt(diag(C'C)./diag(S'S))。

·　gsvd(A,B,0)，“经济”方式分解一般奇异值。

5．舒尔分解

舒尔分解定义式为：

其中A必须是一个方阵，U是一个酉矩阵，S是一个块对角化矩阵，由对角线上的1×1和2×2块组成。特征值可以由矩阵S的对角块给出，而矩阵U给出比特征向量更多的数值特征。此外，对缺陷矩阵也可以进行舒尔分解。

MATLAB 7.0中用函数schur()来进行舒尔分解，其调用格式如下。

·　[U,S]＝schur(A)，返回酉矩阵U和块对角矩阵S。

·　S＝schur(A)，仅返回块对角矩阵S。

如果矩阵A是一个实矩阵，则有两种求解方式。

·　schur(A,'real')，返回的实特征值放在对角线上，而把复特征值放在对角线上的2×2块中。

·　schur(A,'complex')，返回的矩阵S是上三角矩阵，并且如果矩阵A有复特征值，则矩阵S是复矩阵。

函数rsf2csf()可以把实数形式的舒尔矩阵转换成复数形式的舒尔矩阵。

例如，对4阶魔方矩阵做舒尔矩阵，具体代码如下：

由上述语句得到如下代码：

3.1.4　矩阵的特征值和特征向量

一个n×n的方阵A的特征值λ和特征向量v满足下列关系式的变量：

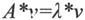
其中，λ为一个标量，v为一个向量。如果把矩阵A的所有n个特征值放在矩阵D的对角线上，相应的特征向量按照与特征值对应的顺序排列，作为矩阵V的列，特征值问题可以改写为：

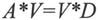
如果V是非奇异的，该问题可以认为是一个特征值分解问题，此时关系式如下：

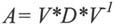
广义特征值问题是指方程AX＝λB*X的非平凡解问题。其中A和B都是n×n的矩阵，λ是一个标量。满足方程的λ称为广义特征值，对应的向量X称为广义特征向量。

MATLAB 7.0中用函数eig()来进行求特征值和特征向量，其调用格式如下。

·　d＝eig(A)，返回矩阵A的所有特征值。

·　[V,D]＝eig(A)，返回矩阵A的特征值和特征向量，它们满足如下关系：AV＝VD

·　[V,D]＝eig(A,'nobalance')，在求解特征值和特征向量时不采用初期的平衡步骤。一般来说平衡步骤对输入矩阵进行调整，这使得计算出的特征值和特征向量更加准确。然而如果输入矩阵中确实含有值很小的元素（可能会导致截断误差），平衡步骤有可能加大这种误差，从而得到错误的特征值和特征向量。

·　d＝eig(A,B)，返回矩阵A和B的广义特征值。

·　[V,D]＝eig(A,B)，返回矩阵A和B的广义特征值和广义特征向量。

·　[V,D]＝eig(A,B,flag)，flag有'chol'和'qz'两种值。当flag＝'chol'时，计算广义特征值采用B的Cholesky分解来实现。当flag＝'qz'时，无论矩阵的对称性如何，都采用QZ算法来求解广义特征值。

例如，求解矩阵A的特征值和特征向量，具体代码如下：

由上述语句得到如下代码：

由上式可以看出矩阵A的特征值中有两个是相同的，与之对应的是矩阵A的特征向量也有两个是相同的。故矩阵V是奇异矩阵，该矩阵不可以做特征值分解。

对于稀疏矩阵，MATLAB 7.0提供函数eigs()来计算模最大的前k个特征值，该函数的具体用法参见METLAB7.0的在线帮助。

3.1.5　非线性矩阵运算

MATLAB 7.0提供的非线性矩阵运算函数及其功能如表3-4所示。

表3-4　　　　　　三角函数

下面将详细介绍这几个函数的用法。

1．矩阵指数运算

以一个线性微分方程组为例进行讲解，示例如下：

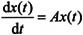
其中x(t)是与时间有关的一个向量，A是与时间无关的矩阵。该方程的解可以表示为：

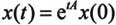
因此，解一个线性微分方程组的问题就等效于计算矩阵指数运算。在MATLAB 7.0中函数expm()用于计算矩阵指数运算。其调用格式如下。

Y＝expm(X)，返回矩阵X的指数

例如，一个三元的线性方程组，其矩阵A为3×3的矩阵，初值x(0)为3×1的向量，求该线性方程组的解，具体代码如下：

由上述语句得到如图3-3所示的结果图。

注意：矩阵指数运算函数expm()是对整个矩阵作指数运算，它有别于矩阵元素的指数运算exp()，具体内容将在3.2.2节中介绍。

2．矩阵对数运算

矩阵对数运算是矩阵指数运算的逆运算，在MATLAB 7.0中函数logm()用来实现矩阵对数运算，其调用格式如下。

·　L＝logm(A)，返回矩阵A的对数L。

·　[L,exitflag]＝logm(A)，返回矩阵A的对数L，同时返回标量exitflag。当exitflag为时，函数成功运行；当exitflag为1时，表明运算过程中某些泰勒级数不收敛，但运算结果仍可能是精确的。

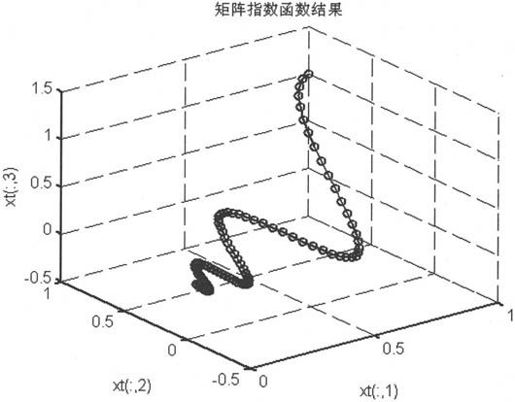
图3-3　矩阵指数函数结果

例如，下面例子说明函数logm()是函数expm()的反函数，具体代码如下：

由上面的语句得到如下代码：

由结果可以看出函数logm()是函数expm()的反函数。

注意：矩阵对数运算函数logm()是对整个矩阵作对数运算，它有别于将在3.2.2小节中介绍的矩阵元素的对数运算log()。

3．矩阵开平方运算

对矩阵A开平方得到矩阵X，满足X*X＝A。如果矩阵A的某个特征值具有负实部，则其平方根X为复数矩阵。如果矩阵A是奇异的，则它有可能不存在平方根X。在MATLAB 7.0中有两种计算矩阵平方根的方法：A^0.5和sqrtm(A)。函数sqrtm()比A^0.5的运算精度更高。函数sqrtm()的调用方法如下：

·　X＝sqrtm(A)，返回矩阵A的平方根X，如果矩阵A是奇异的，将返回警告信息。

·　[X,resnorm]＝sqrtm(A)，不返回任何警告信息，返回留数norm(A－X^2,'fro')／norm(A,'fro')

·　[X,alpha,condest]＝sqrtm(A)，返回一个稳定因子alpha，以及矩阵X的条件数估计condest。

例如，求一个正定矩阵A的平方根X，并验证X*X＝A，具体代码如下：

由上述语句得到如下代码：

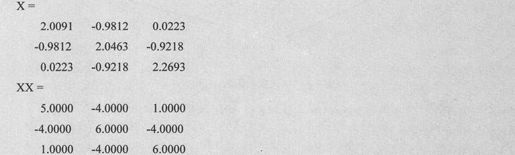
由X*X与矩阵A相等，验证了运算的正确性。

注意：矩阵开平方运算函数sqrtm()是对整个矩阵作开平方运算，它有别于对矩阵元素的开平方运算.^0.5。

4．一般非线性矩阵运算

MATLAB 7.0提供了计算一般非线性矩阵运算的函数funm()，其基本调用格式如下。

·　F＝funm(A,fun)，把函数fun作用在方阵A上，其中fun是一个函数句柄。函数fun的格式是fun(X,k)，其中X是一个向量，k是一个标量。fun(X,k)返回的值应该是fun代表的函数的k阶导数作用在向量X的值。fun代表的函数的泰勒展开在无穷远处必须是收敛的（函数logm()是惟一的例外）。

MATLAB 7.0中可以使用的函数fun如表3-5所示。

表3-5　　　　　　一般非线性矩阵运算函数

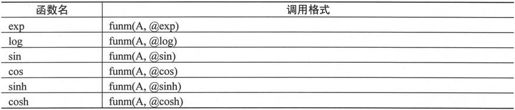
计算矩阵的指数时，表达式funm(A,@exp)和xpm(A)中哪种方式的计算精度更高取决于矩阵A本身的性质。

例如，计算矩阵A的正弦函数，具体代码如下：

由上述语句得到计算如下代码：

3.2　矩阵元素的数学函数

本小节介绍矩阵元素的数学函数，包括三角函数、指数对数函数、复数函数、截断函数和求余函数。这些函数共同的特点是函数的运算都是针对矩阵的元素，即它们都是对矩阵中的每个元素都进行运算。

3.2.1　三角函数

MATLAB 7.0提供的三角函数及其功能如表3-6所示。

表3-6　　　　　　三角函数

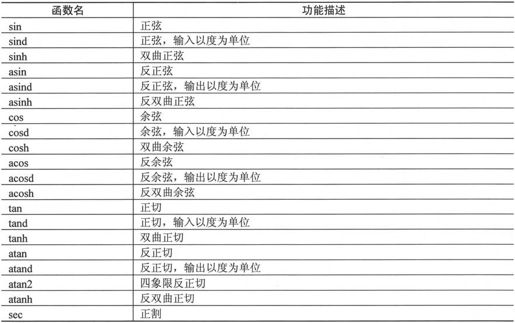
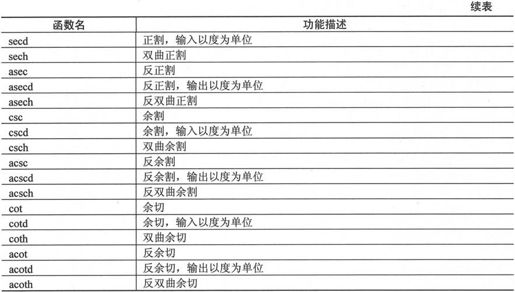
例如，计算0°～360°的正弦函数、余弦函数和它们平方和的值，具体代码如下：

由上述语句得到如图3-4所示的结果图。

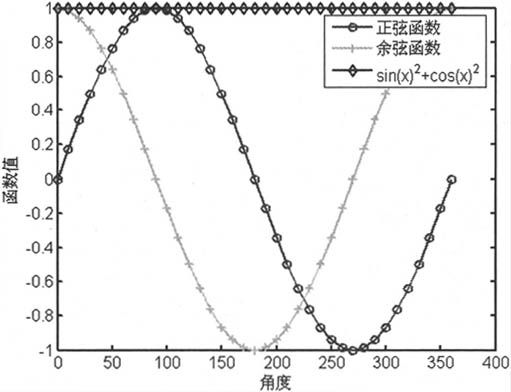
图3-4　三角函数示意图

3.2.2　指数和对数函数

MATLAB 7.0提供的指数、对数函数及其功能如表3-7所示。

表3-7　　　　　　指数和对数函数

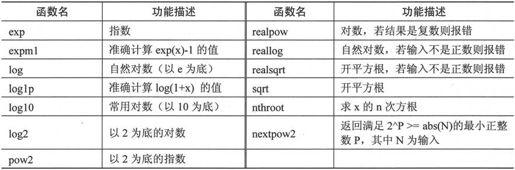
例如，计算e^x和2^x的值，具体代码如下：

由上述语句得到如图3-5所示的示意图。

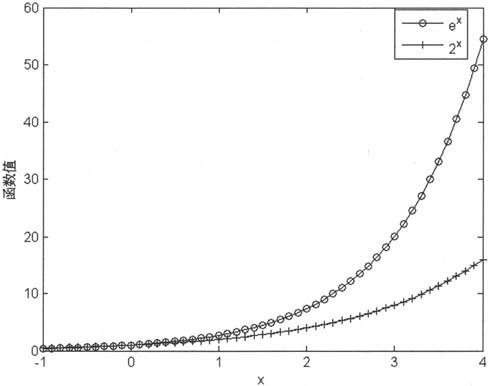
图3-5　指数函数示意图

3.2.3　复数函数

MATLAB 7.0提供的复数函数及其功能如表3-8所示。

表3-8　　　　　　复数函数

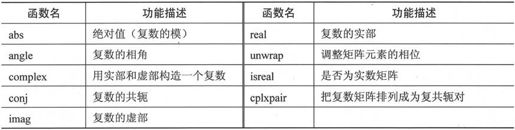
复数函数中除了函数unwrap()和cplxpair()的用法比较复杂外，其他函数都比较简单。下面就详细介绍函数unwrap()和cplxpair()。

函数unwrap()用于对表示相位的矩阵进行校正，当矩阵相邻元素的相位差大于设定阈值（默认值为π）时，函数unwrap()通过加±2π来校正相位。函数unwrap()的基本调用格式如下。

·　Q＝unwrap(P)，当相位大于默认阈值π时，矫正相位；

·　Q＝unwrap(P,tol)，用tol来设定阈值；

·　Q＝unwrap(P,[],dim)，用默认阈值π在给定维dim上做相位矫正；

·　Q＝unwrap(P,tol,dim)，用阈值tol在给定维dim上做相位矫正。

例如，下面数据是滤波器的相位响应，其中w为频率，p为相位。下面程序将比较数据校正前和程序后的差别，具体代码如下：

程序得到结果如图3-6所示。由图可见，原始数据中频率3000Hz～3500Hz之间，相位变化了3.5873（单位：弧度），大于默认的阈值，因此unwrap()函数通过把相位减去2π从而把相位跳变校正为2.6959。

函数cplxpair()把复数数组排列成复数的共轭对。函数cplxpair()的基本调用格式如下。

·　B＝cplxpair(A)，以默认的误差容限100*eps寻找复数的共轭对；

·　B＝cplxpair(A,tol)，以指定的误差容限tol寻找复数的共轭对；

·　B＝cplxpair(A,[],dim)，在dim维度上，以默认的误差容限寻找复数的共轭对；

·　B＝cplxpair(A,tol,dim)，在dim维度上，以指定的误差容限tol寻找复数的共轭对。

如果输入矩阵的复数个数是奇数或者在误差容限内复数不能组合成共轭对，MATLAB 7.0将返回如下错误信息：

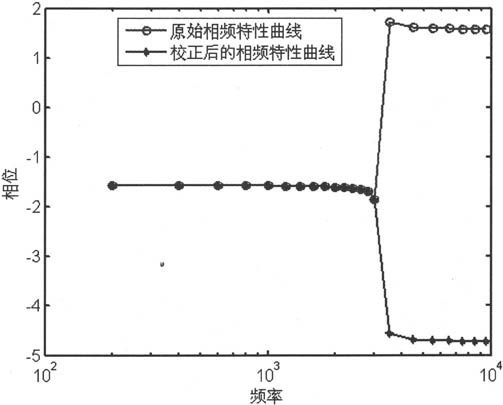
图3-6　unwrap()函数

例如，把复数数组排列成复数的共轭对，具体代码如下：

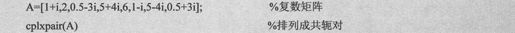
由上述语句输出如下代码：

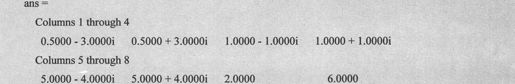
3.2.4　截断和求余函数

MATLAB 7.0提供的截断和求余函数及其功能如表3-9所示。

表3-9　　　　　　截断和求余函数

采用下面的例子来说明函数fix()、floor()、ceil()和round()的区别，具体代码如下：

由上述语句得到如下代码：

用下面的例子说明函数mod()和rem()的区别，具体代码如下：

由上述语句得到如下代码：

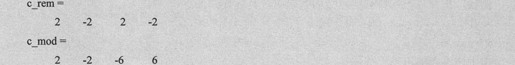
求矩阵的符号使用函数sign()，示例代码如下：

由上述语句得到如下代码：

3.3　特殊数学函数

本小节介绍一些用途比较特殊的数学函数，包括特殊函数、数论函数和坐标变换函数。

3.3.1　特殊函数

特殊函数通常是数学物理方程的解，并且经常在数学、物理和工程问题中出现。MATLAB 7.0提供的特殊函数及其功能如表3-10所示。

表3-10　　　　　　特殊函数

在后面的章节将详细介绍这些特殊函数的定义和用法。为了阅读方便，把这些特殊函数进行分类，包括：Airy函数、Bessel函数、Gamma函数、Beta函数、Jacobi椭圆函数和完全椭圆积分、误差函数、指数积分函数和连带勒让德函数。

1．Airy函数

Airy函数是微分方程的解。有两类Airy函数：第一类Airy函数Ai(Z)和第二类Airy函数Bi(Z)。它们可以用改进的第一类Bessel函数I_v(Z)和改进的第二类Bessel函数K_v(Z)来定义，表达式如下：

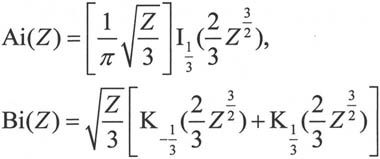
函数Airy()的调用方式如下：

·　W＝Airy(Z)，返回第一类Airy函数Ai(Z)；

·　W＝Airy(0,Z)，与Airy(Z)相同；

·　W＝Airy(1,Z)，返回第一类Airy函数Ai(Z)的导数Ai'(Z)；

·　W＝Airy(2,Z)，返回第二类Airy函数Bi(Z)；

·　W＝Airy(3,Z)，返回第二类Airy函数Bi(Z)的导数Bi'(Z)。

2．Bessel函数

Bessel函数是微分方程的解，其中v是常量。该方程有两个线性无关的解，第一类Bessel函数J_v(Z)和第二类Bessel函数Y_v(Z)，它们的表达式如下：

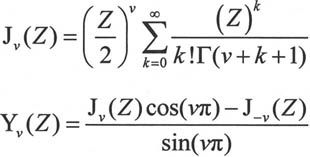
有时也采用Hankel函数来表示Bessel方程，它们是第一类Bessel函数和第二类Bessel函数的线性组合：

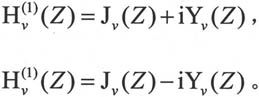
Hankel函数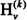也称为第三类Bessel函数。

在MATLAB 7.0中与Bessel函数相关的函数的调用方式如下。

·　J＝besselj(nu,Z)，返回第一类Bessel函数J_v(Z)；

·　J＝besselj(nu,Z,1)，besselj(nu,Z).*exp(-abs(imag(Z)))；

·　Y＝bessely(nu,Z)，返回第二类Bessel函数Y_v(Z)；

·　Y＝bessely(nu,Z,1)，返回bessely(nu,Z).*exp(-abs(imag(Z)))；

·　H＝besselh(nu,K,Z)，返回第三类Bessel函数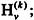

·　H＝besselh(nu,Z)，返回

改进的Bessel函数是微分方程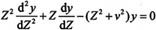的解，其中v是常量。该方程有两个线性无关的解：第一类改进的Bessel函数I_v(Z)和第二类改进的Bessel函数K_v(Z)，它们的表达式如下：

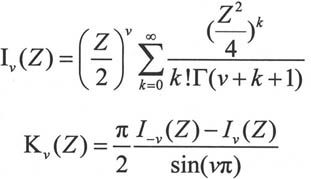
在MATLAB 7.0中与改进的Bessel函数相关的函数的调用方式如下。

·　I＝besseli(nu,Z)，返回第一类改2进的Bessel函数I_v(Z)；

·　I＝besseli(nu,Z,1)，返回besseli(nu,Z).*exp(-abs(real(Z)))；

·　K＝besselk(nu,Z)，返回第二类改进的Bessel函数K_v(Z)；

·　K＝besselk(nu,Z,1)，返回besselk(nu,Z).*exp(Z)。

3．Gamma函数和Beta函数

在MATLAB 7.0中，Gamma函数和Beta函数的定义如下。

·　Gamma函数：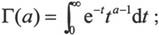

·　不完全Gamma函数：

·　多Γ函数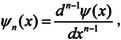：其中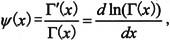ψ_n(x)称为(n＋1)Γ函数，例如ψ₃(x)称为4Γ函数；

·　Beta函数：

·　不完全Beta函数：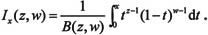

在MATLAB 7.0中与Gamma函数和Beta函数相关的函数的调用方式如下。

·　Y＝gamma(a)，返回Gamma函数Γ(a)；

·　Y＝gammainc(x,a)，返回不完全Gamma函数P(x,a)；

·　Y＝gammainc(X,A,tail)，当tail＝'lower'时返回P(x,a)，当tail＝'upper'时返回1－P(x,a)；

·　Y＝gammaln(A)，返回ln(Γ(a))，可以避免采用log(gamma(a))造成的溢出情况；

·　Y＝psi(X)，返回双Γ函数ψ₁(x)；

·　Y＝psi(k,X)，返回k＋2Γ函数ψ_k＋1(x)；

·　B＝beta(z,w)，返回Beta函数B(z,w)；

·　I＝betainc(x,z,w)，返回不完全Beta函数I_x(z,w)；

·　L＝betaln(z,w)，返回ln(B(z,w))，可以避免采用log(beta(a))造成的溢出情况。

4．Jacobi椭圆函数和完全椭圆积分

Jacobi椭圆函数sn(u)、cn(u)和dn(u)是定义在勒让德第一类椭圆积分基础上的。其中，勒让德第一类椭圆积分表达式如下：

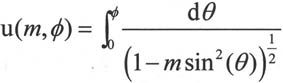
椭圆积分的反函数定义为φ＝am(u)，则sn(u)、cn(u)和dn(u)的表达式为：

第一类完全椭圆积分K(m)也是定义在勒让德第一类椭圆积分基础上的，其表达式如下：

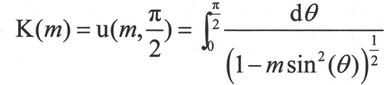
第二类完全椭圆积分E(m)的定义如下：

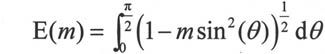
在MATLAB 7.0中与Jacobi椭圆函数和完全椭圆积分相关的函数的调用方式如下。

·　[SN,CN,DN]＝ellipj(U,M)，返回Jacobi椭圆函数sn(u)，cn(u)和dn(u)；

·　[SN,CN,DN]＝ellipj(U,M,tol)，以指定精度tol计算Jacobi椭圆函数，默认精度是eps，若指定一个更大的值会降低计算精度，提高计算速度；

·　K＝ellipke(M)，返回第一类完全椭圆积分K(m)；

·　[K,E]＝ellipke(M)，返回第一类完全椭圆积分K(m)和第二类完全椭圆积分E(m)；

·　[K,E]＝ellipke(M,tol)，以精度指定tol计算完全椭圆积分，若指定一个更大的值会降低计算精度，提高计算速度。

5．误差函数

与误差函数有关的表达式如下：

·　误差函数：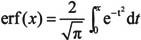

·　余误差函数：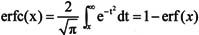

在MATLAB 7.0中与误差函数相关的函数的调用方式如下。

·　Y＝erf(X)，返回误差函数；

·　Y＝erfc(X)，返回余误差函数；

·　Y＝erfcx(X)，返回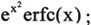

·　X＝erfinv(Y)，返回误差函数的反函数；

·　X＝erfcinv(Y)，返回余误差函数的反函数。

6．指数积分函数

指数积分表达式为：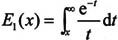

在MATLAB 7.0中用函数expint()计算指数积分，其调用格式如下。

Y＝expint(X)，返回指数积分E₁(x)。

7．连带勒让德函数

连带勒让德函数是连带勒让德方程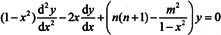的解，记为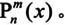连带勒让德函数可以用勒让德多项式来表示，表达式如下：

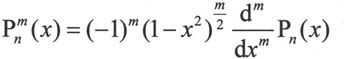
其中P_n(x)为勒让德多项式，其表达式如下：

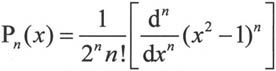
有时需要对连带勒让德函数进行归一化，有施密特半归一化和完全归一化两种方法。施密特半归一化后的连带勒让德函数记为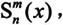它与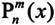的关系如下：

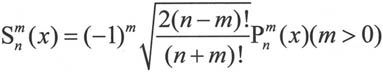
完全归一化方法的目的是为了使归一化后的连带勒让德函数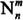(x)满足下式：

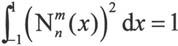
完全归一化后的连带勒让德函数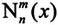与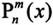的关系如下：

在MATLAB 7.0中函数legendre()用于连带勒让德函数，其调用格式如下。

·　P＝legendre(n,X)，返回连带勒让德函数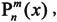m＝0,1,…,n，n必须是标量整数，x必须在［-1，1］范围内的实数。如果X是1×q的向量，则P是（n＋1）×q的矩阵，矩阵元素P（m＋1，i）代表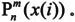一般来说，矩阵P总是比矩阵X多一个维度；

·　S＝legendre(n,X,'sch')，返回施密特半归一化后的连带勒让德函数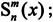

·　N＝legendre(n,X,'norm')，返回完全归一化后的连带勒让德函数

3.3.2　数论函数

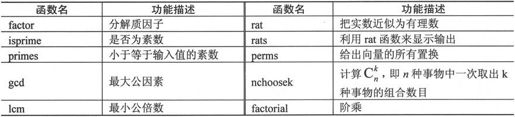
MATLAB 7.0提供的数论函数及其功能如表3-11所示。

表3-11　　　　　　数论函数

例如，求78的所有质因子，具体代码设置如下：

由上述语句得到如下代码：

例如，求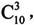具体代码设置如下：

由上述语句得到如下代码：

3.3.3　坐标变换函数

MATLAB 7.0提供的坐标变换函数及其功能如表3-12所示。

表3-12　　　　　坐标变换函数

例如，把笛卡尔坐标系中的点（1，1，1）分别转换到球坐标系和极坐标系中，代码设置如下：

由上述语句得到如下代码：