第6章　数据分析

数据分析和处理是各种应用中非常重要的问题。针对数据分析和处理，MATLAB 7.0提供大量的函数方便用户使用。本章将介绍MATLAB 7.0强大的数据分析和处理功能。

本章6.1小节介绍多项式函数，这些函数用于多项值求值、多项式乘法、多项式除法、多项式求导等。6.2小节介绍插值函数。MATLAB 7.0提供数个不同的插值算法，这些算法的性能比较将在本小节中详细介绍。6.3小节涵盖内容比较多，包括基本的数据分析函数（例如矩阵的平均值）、协方差和相关矩阵、有限差分和梯度、信号滤波和卷积以及傅立叶变换。6.4小节介绍功能函数，包括函数的表示方法、函数的画图、函数的最小值和最大值、函数的数值积分以及在功能函数中使用参数的方法。6.5小节介绍了三类微分方程组问题的解法，包括常微分方程组的初值问题、延迟微分方程组数值解和常微分方程组的边界问题。

6.1　多项式函数

MATLAB 7.0提供了一些处理多项式的基本函数，如求多项式的值、多项式的根和多项式的微分等。另外，MATLAB 7.0也提供了一些高级函数处理多项式，如曲线拟合和多项式的部分分式表示。这些函数保存在MATLAB 7.0工具箱的polyfun子目录下，如表6-1所示。

表6-1　　　　　　多项式函数

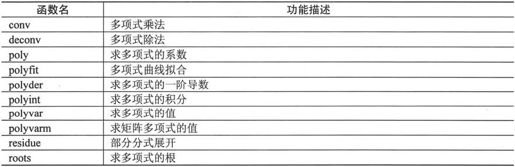
此外在MATLAB 7.0的符号工具箱（Symbolic Math Toolbox）中还有一些是用于处理多项式的函数，在表6-1中没有提到。

6.1.1　多项式表示法

MATLAB 7.0采用行向量来表示多项式，将多项式的系数按降幂次序存放在行向量中。多项式P(x)＝a₀xⁿ＋a₁x^n－1＋…＋a_n－1x＋a_n的系数行向量为P＝[a₀a₁…a_n]，注意顺序必须是从高次幂到低次幂。例如，多项式x⁴＋3x³＋4x＋5可以用系数向量[1 3 0 4 5]来表示，注意多项式中缺少的幂次要用“0”补齐。

例如，设计一个函数poly2str()，实现把一个行向量表示的多项式转换为常见的字符串表示的多项式，代码设置如下：

以下语句说明了函数poly2str()的用法：

上述语句得到输出代码如下：

上面字符串中x^n表示x的n次幂。

例如，设计一个函数实现从多项式的字符串表示转换为多项式的行向量表示，要求输入不必降幂排列，并且函数具有实现多项式同类项合并功能，代码设置如下：

以下语句把一个多项式的字符串表示转换为一个多项式的向量表示，然后再把多项式的向量表示转回成多项式的字符串表示，代码设置如下：

由上述语句得到输出代码如下：

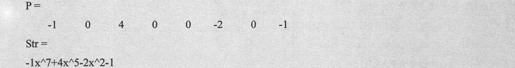
由上述结果可以看出，输入多项式的同类项被合并了，这正是我们设计函数str2poly()时所希望的。

6.1.2　多项式求值

在MATLAB 7.0中使用函数polyval()来计算多项式的值。其调用方式如下：

·　y＝polyval(p,x)，p为行向量形式的多项式，x代入多项式的值，它可以是标量、向量和矩阵。如果x是向量或者矩阵，那么该函数将对向量或者矩阵的每一个元素计算多项式的值，并返回给y。

MATLAB 7.0不但可以计算矩阵元素的多项式值，也可以把整个矩阵代入多项式作为自变量进行计算。计算矩阵多项式值的函数是polyvalm()，其调用方式如下：

·　Y＝polyvalm(p,X)，把矩阵X代入多项式p中进行计算，其中矩阵X必须是方阵。

例如，求多项式的值和矩阵多项式的值，请注意这两者的区别，具体代码如下：

由上述语句得到输出代码如下：

6.1.3　多项式乘法和多项式除法

多项式乘法和除法运算也就是多项式向量的卷积和解卷积运算。在MATLAB 7.0中，函数conv()和deconv()用来实现这些运算。这两个函数的调用格式如下。

·　w＝conv(u,v)，实现向量u,v的卷积，在代数上相当于多项式u乘上多项式；

·　[q,r]＝deconv(v,u)，实现解卷积运算，他们之间的关系为v＝conv(u,q)＋r。在代数上相当于实现多项式u除以v，得到商q和余多项式r。

例如，求多项式x²＋2x＋3与多项式2x²＋3x＋4的乘积，代码设置如下：

上述语句得到输出如下：

为了直观，上面程序利用了6.1.1小节中的多项式的字符串表示与多项式的向量表示的互换函数。

例如，求上个例子中的多项式乘积结果2x⁴＋7x³＋16x²＋17x＋12除以多项式x²＋2x＋3的商，代码设置如下：

由上述语句得到输出代码如下：

6.1.4　多项式的导数和微分

1．多项式的导数

在MATLAB 7.0中使用函数polyder()来计算多项式的导数，其调用方式如下：

·　k＝polyder(p)，返回多项式p的导数；

·　k＝polyder(a,b)，返回多项式a与多项式b乘积的导数；

·　[q,d]＝polyder(b,a)，返回多项式a除以b的商的导数，并以q/d格式表示。

例如，对多项式求导，代码设置如下：

由上述语句得到输出代码如下：

2．多项式的积分

在MATLAB 7.0中使用函数polyint()来计算多项式的积分，其调用方式如下：

·　polyint(p,k)，返回多项式p的积分，设积分的常数项为k；

·　polyint(p)，返回多项式p的积分，设积分的常数项为0。

例如，求多项式3x²＋4x＋5的积分，代码设置如下：

由上述语句得到输出代码如下：

6.1.5　多项式的根和由根创建多项式

1．多项式的根

在MATLAB 7.0中使用函数roots()来求多项式的根，其调用方式如下：

·　r＝roots(c)，返回多项式c的所有根r，r是向量，其长度等于根的个数。

例如，求多项式2x³－2x²－8x＋8的根，代码设置如下：

由上述语句得到输出代码如下：

2．由根创建多项式

与多项式求根相反的过程是由根创建多项式，它由函数poly()来实现，其调用格式如下：

·　p＝poly(r)，输入r是多项式所有根，返回值为代表多项式的行向量形式；

·　p＝poly(A)，输入是N×N的方阵，返回值p是长度为N＋1的行向量多项式，它是矩阵A的特征多项式，也就是说多项式p的根是矩阵A的特征值。

例如，由根[-2 2 1]创建多项式，代码设置如下：

由上述语句得到输出代码如下：

例如，求矩阵的特征多项式，代码设置如下：

由上述语句得到输出代码如下：

6.1.6　多项式部分分式展开

函数residue()可以将多项式之比用部分分式展开，也可以将一个部分分式表示为多项式之比。函数residue()的调用格式如下：

·　[r,p,k]＝residue(b,a)，求多项式之比b/a的部分分式展开，返回值r是部分分式的留数，p是部分分式的极点，k是直接项。如果多项式a没有重根，部分分式的形式如下：

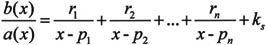
其中向量r，p的长度和向量a，b的长度有如下关系：

当向量b的长度小于a时，向量k中没有元素，否则应满足如下关系：

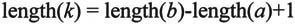
·　[b,a]＝residue(r,p,k)，从部分分式得到多项式向量。

例如，求多项式之比的部分分式展开，然后在把部分分式表示为多项式之比的形式，代码设置如下：

由上述语句得到输出代码如下：

6.1.7　多项式曲线拟合

函数polyfit()采用最小二乘法对给定数据进行多项式拟合，最后给出多项式的系数。该函数的调用方式如下：

·　p＝polyfit(x,y,n)，采用n次多项式p来拟合数据x和y，从而使得p(x)与y最小均方差最小。

例如，下面例子说明函数polyfit()的用法，并讨论采用不同多项式阶数对拟合结果的影响，代码设置如下：

得到输出如图6-1所示。由图6-1可以看出：使用5次多项式拟合时，拟合得到的结果比较差。而使用8次多项式拟合时，得到的结果与原始数据符合得很好。但使用60次多项式拟合时，拟合的结果非常差。可见用多项式拟合必须选择适中的阶数，而不是阶数越高精度越高。

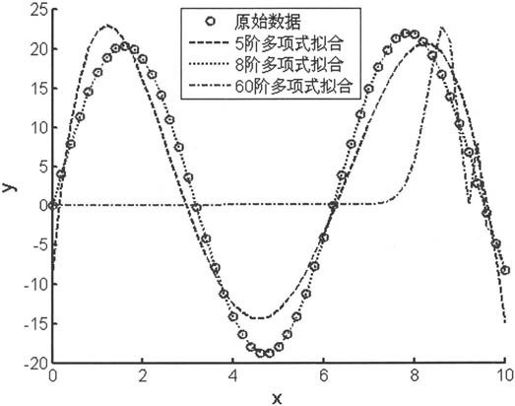
图6-1　多项式曲线拟合

6.1.8　曲线拟合图形用户接口

为了方便用户的使用，MATLAB 7.0提供了支持曲线拟合的图形用户接口。它位于“Figure”窗口的“Tools\Basic Fitting”菜单中。为了使用该工具，首先用待拟合的数据画图，代码设置如下：

得到“Figure”窗口，如图6-2所示。然后在“Figure”窗口中点击菜单“Tools\Basic Fitting”，得到“Basic Fitting”窗口，如图6-3所示。可以单击“Basic Fitting”窗口右下角的向右按钮，得到“Basic Fitting”窗口的全貌，如图6-4所示。

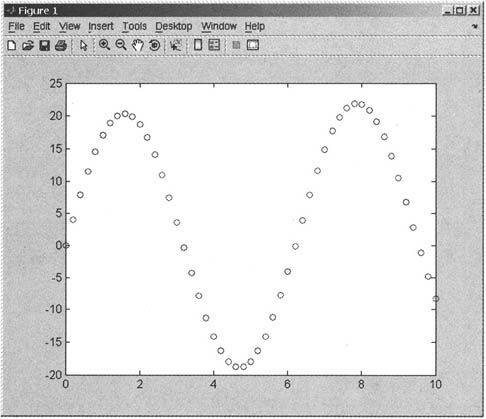
图6-2　“Figure”窗口

图6-3　Basic Fitting窗口

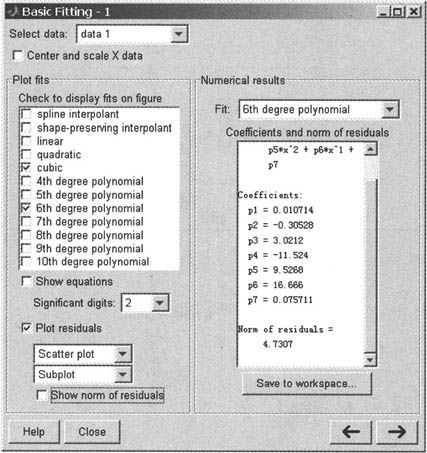
图6-4　“Basic Fitting”窗口全貌

在“Basic Fitting”窗口的“Plot fits”复选框中选择“cubic”和“6th degree polynomial”这两选项，然后单击“Plot residuals”单选框使之处在选上状况，最后把“Plot residuals”单选框正下方的下拉列表选择为“Scatter plot”。在这些操作后，“Figure”窗口已经出现拟合好的数据，并且画出拟合数据的残留误差residuals（如图6-5所示）。同时拟合结果也在“Basic Fitting”的“Numerical results”中显示出来。

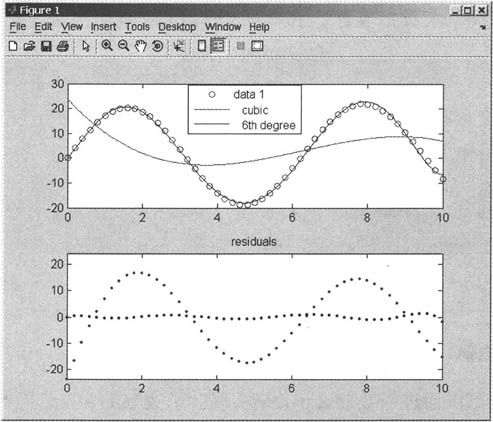
图6-5　数据拟合结果

6.2　插值

插值是在已知数据之间寻找估计值的过程。在信号处理和图像处理中，插值是极其常用的方法。MATLAB 7.0提供大量的插值函数。这些函数在获得数据的平滑度、时间复杂度和空间复杂度方面上有不同的性能。

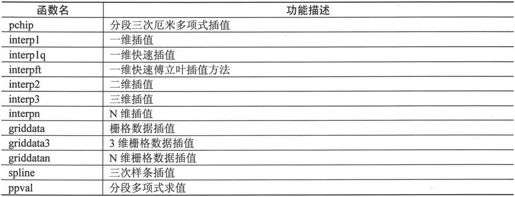
插值函数保存在MATLAB 7.0工具箱的polyfun子目录下，如表6-2所示。

表6-2　　　　　　插值函数

6.2.1　一维插值

一位插值就是对一维函数y＝f(x)进行插值，图6-6显示了插值的含义，实心点（x,y）代表的是已知数据，空心点（xi,yi）的横坐标xi代表需要估计值的位置，纵坐标yi表示插值后的估计值。在MATLAB 7.0中，一维插值有基于多项式的插值和基于快速傅立叶的插值两种类型。

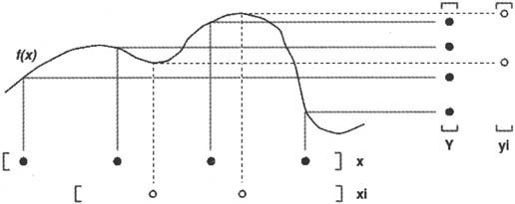
图6-6　一维插值示意图

1．一维多项式插值

一维多项式插值可以通过函数interp1()来实现。函数interp1()的基本调用格式如下。

·　yi＝interp1(x,y,xi,method)，x必须是向量，y可以是向量也可以是矩阵。如果y是向量，则必须与x具有相同的长度，这时xi可以是标量、向量和任意维矩阵，yi与xi具有相同的大小；如果y是矩阵，则其大小必须是[n,d1,d2,…,dk]（n为向量x的长度），函数对dld2…*dk组y值都进行插值；

·　yi＝interp1(y,xi)，默认x为1:n，其中n为向量y的长度；

·　yi＝interp1(x,y,xi,method)，输入变量method用于指定插值的方法。可采用的插值方法将在本小节详细介绍；

·　yi＝interp1(x,y,xi,method,'extrap')，对超出数据范围的插值数据指定外推方法'extrap'；

·　yi＝interp1(x,y,xi,method,extrapval)，对超出数据范围的插值数据返回extrapval值，一般设为NaN或者0；

·　pp＝interp1(x,y,method,'pp')，返回值pp为数据y的分段多项式形式。method指定产生分段多项式pp的方法，它可以是插值方法中除了'v5cubic'的任何方法。

一维插值可以指定的方法如下：

（1）最邻近插值（Nearest neighbor interpolation, method＝'nearest'），这种插值方法在已知数据的最邻近点设置插值点，对插值点的数进行四舍五入。对超出范围的点将返回一个NaN (Not a Number)。

（2）线性插值（Linear interpolation, method＝'linear'），该方法是未指定插值方法时MATLAB7.0默认采用的方法。该方法采用直线连接相邻的两点。对超出范围的点将返回一个NaN (Not a Number)。

（3）三次样条插值（Cubic spline interpolation, method＝'spline'），这样方法采用三次样条函数来获得插值点。在已知点为端点情况下，插值函数至少具有相同的一阶和二阶导数。

（4）分段三次厄米多项式插值（Piecewise cubic Hermite interpolation, method＝'pchip')。

（5）三次多项式插值（method＝'cubic'），与分段三次厄米多项式插值相同。

（6）MATLAB5中使用的三次多项式插值（method＝'v5cubic'），该方法使用一个3次多项式函数对已知数据进行拟合。

当选择一个插值方法时应该考虑方法的执行速度、占用内存大小和获得数据的平滑度。以上方法的特点如下。

（1）最邻近插值：最快的插值方法，但是数据平滑方面最差，其得到的数据是不连续的。

（2）线性插值：比邻近插值占用更多的内存，执行速度也稍慢，但其数据平滑方面优于邻近插值。与邻近插值不同的是，线性插值的数据变化是连续的。

（3）三次样条插值：处理速度最慢，占用内存小于分段三次厄米多项式插值，可以产生最光滑的结果。但是如果输入数据不均匀或者某些点靠得很近，会出现一些错误。样条插值是极其有用的插值方法，因此除了提供三次样条插值函数外，MATLAB 7.0还提供了一个样条插值工具箱，它位于toolbox\splines下。

（4）分段三次厄米多项式插值：处理速度和消耗的内存比线性插值差，但插值得到的数据和一阶导数都是连续的。

这些方法的相对优劣不仅适用于一维插值，而且适用于二维插值情况甚至高维插值情况。

例如，下面例子用不同插值方法对一维数据进行插值，并比较其不同，代码设置如下：

由上述语句得到如图6-7所示的示意图。

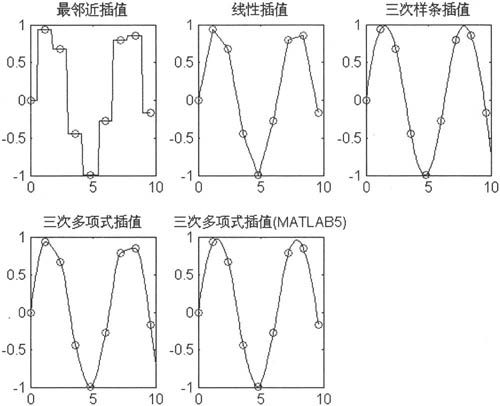
图6-7　一维插值

2．一维快速傅立叶插值

一维快速傅立叶插值通过函数interpft()来实现，该函数用傅立叶变换把输入数据变换到频域，然后用更多点的傅立叶逆变换，变换回时域，其结果是对数据进行增采样。函数interpft()的调用格式如下。

·　y＝interpft(x,n)，对x进行傅立叶变换，然后采用n点傅立叶逆变换变回到时域。如果x是一个向量，数据x的长度为m，采样间隔为dx，则数据y的采样间隔是dx*m/n，注意n值必须大于m；如果x是矩阵，函数操作在x的列上，返回结果与x具有相同的列数但其行数为n；

·　y＝interpft(x,n,dim)，在dim指定的维度上进行操作。

例如，利用一维快速傅立叶插值实现数据增采样，代码设置如下：

由上述语句得到如图6-8所示的示意图。

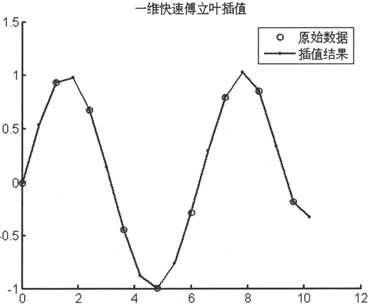
图6-8　一维快速傅立叶插值

6.2.2　二维插值

二维插值主要应用于图像处理和数据的可视化，其基本思想与一维插值相同，它是对两变量的函数z＝f(x,y)进行插值。二维插值的示意图如图6-9所示。

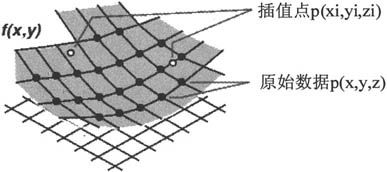
图6-9　二维插值示意图

MATLAB 7.0中的二维插值函数为interp2()，其调用格式如下。

·　zi＝interp2(x,y,z,xi,yi)，原始数据x,y,z决定插值函数z＝f(x,y)，返回值zi是（xi,yi）在函数f(x,y)上的值；

·　zi＝interp2(z,xi,yi)，若z＝n×m，则x＝1:n，y＝1:m；

·　zi＝interp2(z,ntimes)，在两点之间递归地插值ntimes次；

·　zi＝interp2(x,y,z,xi,yi,method)，可采用的插值方法在本小节将详细介绍；

·　zi＝interp2(…,method,extrapval)，当数据超过原始数据范围时，用输入extrapval指定一种外推方法。

二维插值可以采用的插值方法如下：

（1）最邻近插值（Nearest neighbor interpolation, method＝'nearest'），这种插值方法在已知数据的最邻近点设置插值点，对插值点的数进行四舍五入。对超出范围的点将返回一个NaN (Not a Number)。

（2）双线性插值（Bilinear interpolation, method＝'linear'），该方法是未指定插值方法时MATLAB7.0默认采用的方法。插值点的值只决定于最邻近的4个点的值。

（3）三次样条插值（Cubic spline interpolation, method＝'spline'），这样方法采用三次样条函数来获得插值数据。

（4）双三次多项式插值（method＝'cubic'）。

例如，下面例子比较各种二维插值插值算法的不同，如下：

由上述代码得到的效果图如图6-10和图6-11所示。如图6-11所示为插值后数据的等高线，可以用于比较插值后数据的平滑性能。

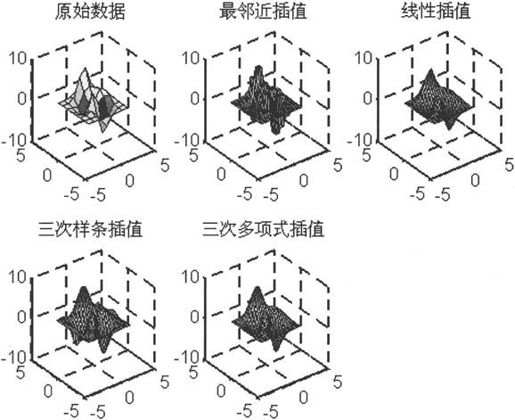
图6-10　二维插值

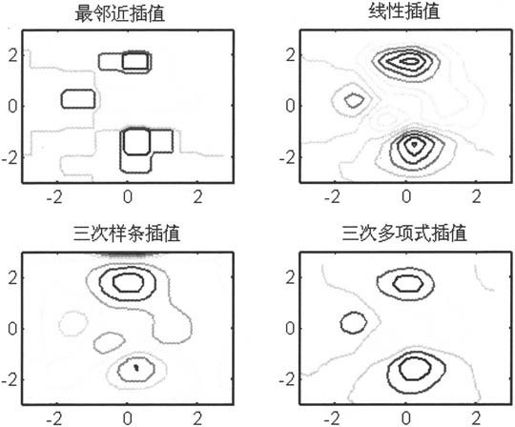
图6-11　二维插值后的等高线

6.3　数据分析和傅立叶变换

MATLAB7.0中与数据分析和傅立叶变换相关的函数位于目录\toolboxs\MATLAB\datafun下，本节将分类介绍这些函数。

MATLAB 7.0在这些函数中的约定。

·　一维统计数据可以用行向量或者列向量来表示，不管输入数据是行向量或者是列向量，运算是对整个向量进行的；

·　二维统计数据可以采用多个向量表示，也可以采用二维矩阵来表示。对二维矩阵运算时，运算总是按列进行的。

这两条约定不仅适用于本节提到的函数，而且适用于MATLAB 7.0各个工具箱的函数。

6.3.1　基本数据分析函数

MATLAB 7.0提供的基本数据分析函数的功能和调用格式如表6-3所示。

表6-3　　　　　　基本数据分析函数

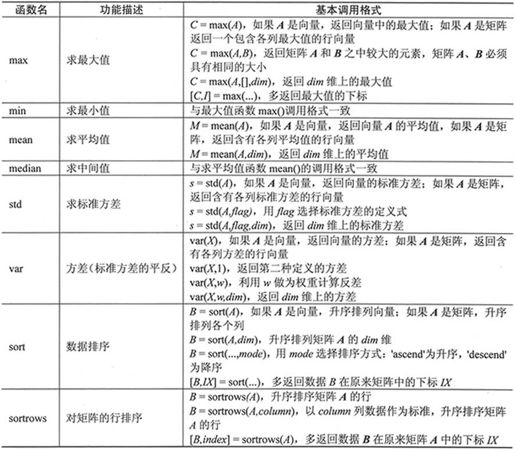
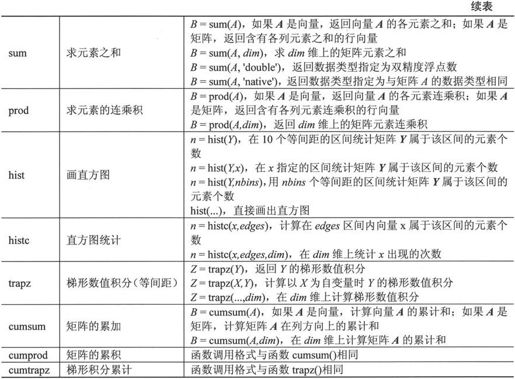
1．最大值、最小值、平均值、中间值、元素求和

这几个函数的用法都比较简单，下面的例子用来说明这些函数的用法：

由上述语句得到的效果如图6-12所示。

图6-12　最大值、最小值、平均值、中间值、元素求和

2．标准方差和方差

向量x的标准方差有如下两种定义：

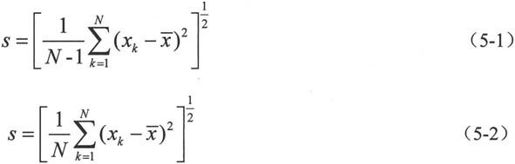
其中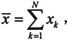N是向量x的长度。

MATLAB 7.0中默认使用（5-1）式来计算数据的标准方差。要使用（5-2）式来计算标准方差可以使用函数调用格式std(A,1)。

方差是标准方差的平反。对应标准方差的两种定义，方差也有两种定义。同样MATLAB 7.0中默认使用（5-1）式来计算数据的方差。要使用（5-2）式来计算方差可以使用函数调用格式var(A,1)。

例如，有一维随机变量x，要求验证2*x的方差是x的4倍，2x标准方差是x的2倍，代码设置如下：

由上述语句得到输出代码如下：

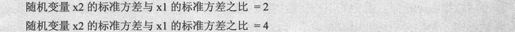
3．元素排序

MATLAB 7.0可以对实数、复数和字符串进行排序。对复数矩阵进行排序时，先按复数的模进行排序，如果模相等则按其在区间[-π，π]上的相角进行排序。MATLAB7.0中实现排序的函数为sort()。

例如，对复数矩阵排列，代码设置如下：

由上述语句得到输出代码如下：

MATLAB 7.0提供函数sortrows()用于对矩阵的行进行排列。

例如，对字符数据进行排列，代码设置如下：

由上述语句得到输出代码如下：

4．基本数据分析实例

例如，需要设计一个函数从已知n个数据中挑选出方差最小的k个数据。显然，如果要穷举所有的情况，计算量将会很大。本例中采用的算法是先对数据进行排队，然后计算所有相邻的k个数据的方差，选出方差最小的相邻k个数据就是所求的数据。本例在排序时记录了排序后数据在未排序数据中的下标，故能同时返回方差最小的k个数据在原来数据中的位置。从已知n个数据中挑选出方差最小的k个数据的函数如下：

可以用下面语句来验证以上函数的正确性，如下：

由上述语句得到输出代码如下：

6.3.2　协方差和相关系数矩阵

在数理统计中，协方差和相关函数是极其重要的随机变量的数字特征。若给定n维随机变量x＝(x₁,x₂,…,x_n)，定义

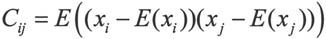
则称

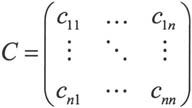
为随机变量x＝(x₁,x₂,…,x_n)的协方差矩阵。定义相关系数：

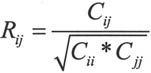
则称

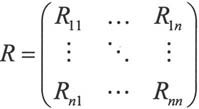
为相关系数矩阵。

在MATLAB 7.0中，3维随机变量的100次抽样数据应该表示为100×3的矩阵，其中矩阵每一列表示随机变量的一个分量，每一行代表一次抽样。

MATLAB 7.0提供函数cov()用于计算随机变量的协方差矩阵，其调用格式如下：

·　C＝cov(X)，计算X代表的随机变量的协方差矩阵。如果X是一个向量，返回向量的方差；如果X是矩阵，返回矩阵的协方差矩阵，其对角元是该列随机变量的方差；

·　C＝cov(x,y)，x和y必须是具有相同长度的向量。相当于计算C＝cov([xy])；

·　cov(X,1)，计算协方差时采用（5-2）式的方差，默认情况采用（5-1）式定义的无偏方差；

·　C＝cov(x,y,1)，计算协方差时采用（5-2）式的方差，默认情况采用（5-1）式定义的无偏方差。

MATLAB 7.0提供函数corrcoef()用于计算随机变量的相关系数矩阵，其调用格式如下。

·　R＝corrcoef(X)，返回X代表的随机变量的相关系数矩阵；

·　R＝corrcoef(x,y)，x和y必须是具有相同长度的向量，相当于计算C＝corrcoef([xy])；

·　[R,P]＝corrcoef(…)，多返回一个P值用来检验不相关的几率。如果随机变量完全相关则P值为0；如果P值很小，例如小于0.05，则可以认为随机变量的相关性很大；

·　[R,P,RLO,RUP]＝corrcoef(…)，多返回与相关系数矩阵R有相同大小的矩阵RLO和RUP，RLO和RUP是相关系数在置信度为95％情况的下界和上界。

例如，计算随机变量的系数相关矩阵，代码设置如下：

由上述语句得到输出代码如下：

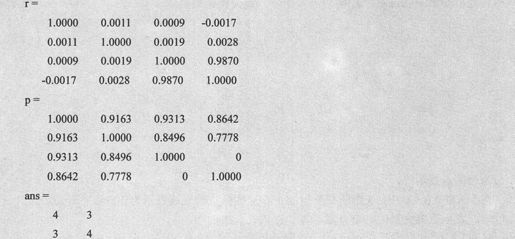
可见，只有随机变量的第3行和随机变量的第4行相关系数才比较大，这正是在程序中故意引入的相关性。

6.3.3　有限差分和梯度

在MATLAB 7.0中使用函数diff()来计算差分，其调用格式如下。

·　Y＝diff(X)，如果X是一个向量，则返回[X(2)－X(1)X(3)－X(2)…X(n)－X(n－1)]；如果X是一个矩阵则返回[X(2:m,:)－X(1:m－1,:)]；

·　Y＝diff(X,n)，返回n阶差分，例如diff(X,2)，与语句diff(diff(X))效果相同；

·　Y＝diff(X,n,dim)，返回在dim维上的n阶差分。

例如，利用有限差分计算正弦函数的导数，代码设置如下：

由上述语句得到如图6-13所示的示意图。

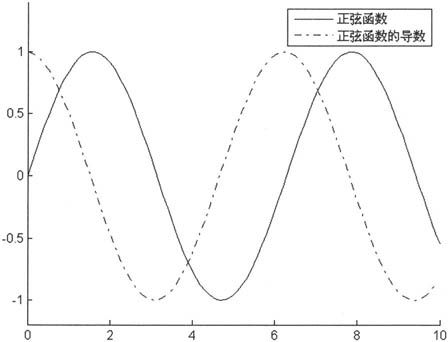
图6-13　正弦函数及其导数

对于一个二元函数F(x,y)，可以定义它的梯度如下：

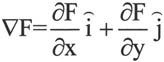
该梯度代表F变化最快的方向。在MATLAB 7.0中，用函数gradient()来计算梯度，其调用格式如下。

·　FX＝gradient(F)，F是一个向量，返回F在x方向上的梯度，相当于计F的微分；

·　[FX,FY]＝gradient(F)，F是二维矩阵，FX是F在x方向的微分（列方向），FY是F在y方向的微分（行方向），并假定自变量的间距是1；

·　[Fx,Fy,Fz,…]＝gradient(F)，F是N维矩阵，返回N个方向的微分值；

·　[…]＝gradient(F,h)，h为一个标量，用于指定所有方向上自变量的间距；

·　[…]＝gradient(F,h1,h2,…)，用多个标量h1,h2,…来指定各个方向上自变量的间距。

例如，计算二维高斯函数的梯度场，代码设置如下：

由上述语句得到如图6-14所示的示意图。图中椭圆是二维高斯函数的等高线，箭头的方向代表梯度的方向，箭头的大小代表梯度的模。由图可见梯度方向总是垂直于等高线的，这是梯度场的基本性质之一。

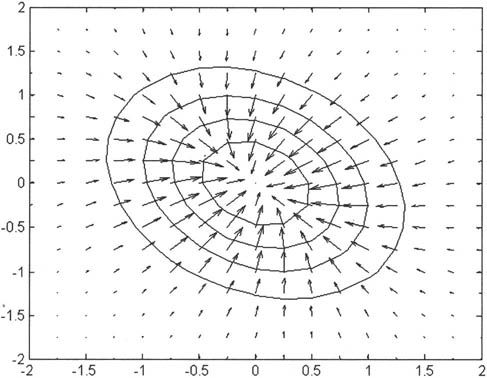
图6-14　二维高斯函数的梯度场

6.3.4　信号滤波和卷积

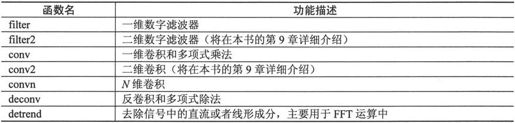
MATLAB 7.0中有关信号滤波和卷积的函数，如表6-4所示。

表6-4　　　　　　信号滤波和卷积函数

1．一维数字滤波

MATLAB 7.0的一维数字滤波可以用函数filter()来实现，它是直接Ⅱ型线性差分方程组的解，可以用于实现FIR和IIR滤波。直接Ⅱ型线性差分方程组的信号流程图如图6-15所示。

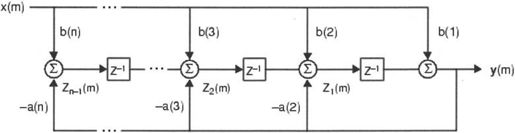
图6-15　直接Ⅱ型线形差分方程组

图6-15的线性差分方程组用如下表达式来表示：

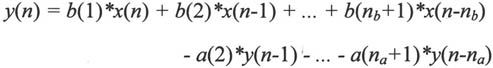
其中n_a和n_b是向量b和a的长度。该方程是n－1阶的线性方程。该方程表现在Z域的形式为：

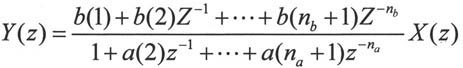
函数filter()的调用格式如下。

·　y＝filter(b,a,X)，X为用于滤波的数据，向量a和b构造一个滤波器，Y为数据X通过滤波器之后的值；

·　[y,zf]＝filter(b,a,X)，多返回一个表示数据延迟时间的量zf。当X为向量时，zf等于max(length(a),length(b))－1；

·　[y,zf]＝filter(b,a,X,zi)，zi为初始数据延迟，zf等于最终数据延迟；

·　y＝filter(b,a,X,zi,dim)，在dim维上进行数据滤波。

如何得到滤波器的系数b和a涉及到滤波器设计问题，具体将在本书的第10章作出详细介绍。在有些情况下，可以很容易得到滤波器的系数b和a。例如，一个5阶平均值滤波器：y(n)＝1/5x(n)＋1/5x(n－1)＋1/5x(n－2)＋1/5x(n－3)＋1/5*x(n－4)，其系数a可以表示为1，系数b可以表示为[1/5 1/5 1/5 1/5 1/5]。

下面通过一个示例来实现对带噪声的正弦信号进行平均值滤波，代码设置如下：

上述语句得到输出如图6-16所示。可见平均值滤波能有效去除信号的噪声。

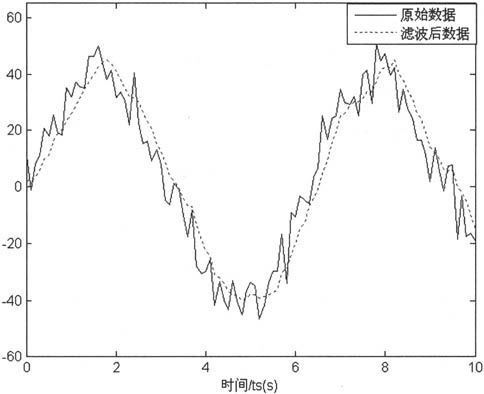
图6-16　平均值滤波

2．信号卷积

向量u和v的卷积为w，则记为w＝u⨂v。如果u，v的长度分别为m和n，则w的长度为m＋n－1。卷积的定义为：

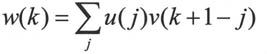
在上式中j可以使u(j)和v(k＋1－j)有意义的任何值。卷积又一个重要的性质，即fft(w)＝fft(u)*fft(v)，在该式中函数fft()表示信号的傅立叶变换。

MATLAB 7.0使用函数conv()来计算卷积。在前面第6.1.3小节，已经介绍了可以用该函数来计算多项式的乘法。函数conv()计算卷积时利用快速傅立叶变换来实现，采用的步骤如下：

·　U＝fft(u)；

·　V＝fft(v)；

·　w＝ifft(u,v)。

例如，计算向量的卷积，代码设置如下：

由上述语句得到如图6-17所示的示意图。

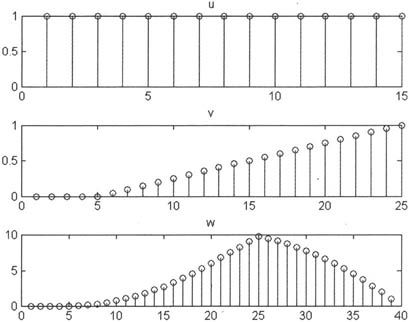
图6-17　信号卷积

3．信号直流或线性成分去除

在做快速傅立叶变换之前经常需要去除信号中的直流成分或者线性成分。MATLAB 7.0提供的detrend()函数就是用于实现去除信号中的直流成分或者线性成分的。其调用格式如下。

·　y＝detrend(x)，如果x是一个向量，从信号x中减去线性成分；如果x是一个矩阵，去除x所有列中的线性成分；

·　y＝detrend(x,'constant')，如果x是一个向量，从信号x中减去直流成分；如果x是一个矩阵，去除x所有列中的直流成分；

·　y＝detrend(x,'linear',bp)，从信号x中减去分段线性函数，分段线性函数的端点由输入bp决定。

例如，从信号中去除直流成分和线性成分，代码设置如下：

由上述语句得到如图6-18所示的示意图。

6.3.5　傅立叶变换

对信号进行分析通常可以在时域中进行，也可以在频域中进行，时域分析方法和频域分析方法各有其优缺点。傅立叶变换是把信号从时域变换到频域，因此它在信号分析中占有极其重要的地位，如滤波器设计、频谱分析等方面。

傅立叶变换既可以对连续信号进行分析，也可以对离散信号进行分析。连续信号的傅立叶变换实际上要计算傅立叶积分，这部分内容可以参见本书第7章。本小节只介绍离散傅立叶变换，即Discrete Fourier Transform (DFT)。

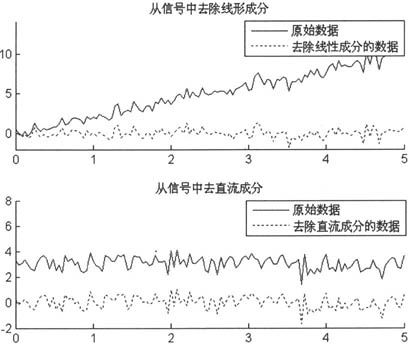
图6-18　去除信号中的直流成分和线性成分

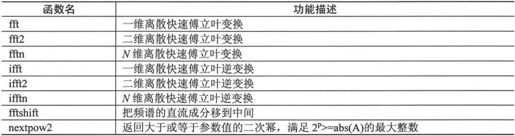
MATLAB 7.0提供的有关傅立叶变换的函数如表6-5所示。

表6-5　　　　　　傅立叶变换函数

1．一维傅立叶变换和一维傅立叶逆变化

一维离散傅立叶变换的定义，如果有一个向量x(n)，其离散傅立叶变换结果为X(k)，X(k)与x(n)的关系如下：

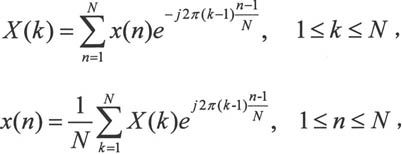
其中N为向量x(n)的长度。

在MATLAB 7.0中一维离散傅立叶变换由函数fft()来实现，其调用方式如下。

·　Y＝fft(X)，如果X是向量，返回向量X的傅立叶变换；如果X是矩阵，函数对矩阵X的每一列进行傅立叶变换；

·　Y＝fft(X,n)，用输入n指定傅立叶变换的长度。如果向量X的长度小于n，则做傅立叶变换之前在向量的尾部添加0值，使得向量X为长度为n；如果向量X的长度大于n，则把向量X截断为长度为n的向量；

·　Y＝fft(X,[],dim)，在dim维上进行傅立叶变换；

·　Y＝fft(X,n,dim)，在dim维上进行傅立叶变换，并指定傅立叶变换的长度。

在MATLAB 7.0中一维离散傅立叶逆变换由函数ifft()来实现，其调用方式基本与函数fft()相同，只是添加一个选项，其调用方式如下。

·　y＝ifft(…,'symmetric')，把频谱X(k)看成是共轭对称。该选项在X(k)不是严格共轭对称时有效；

·　y＝ifft(…,'nonsymmetric')，该选项为默认选项。

与傅立叶变换函数经常使用的函数是fftshift()函数。如图6-19所示，信号x(n)经过FFT后得到频谱X(k)，X(k)的头部和尾部代表信号的低频分量大小，X(k)的中间则代表高频部分。习惯上画频率响应曲线时把直流成分放在曲线的中间，而把高频部分放在曲线的头部和尾部。因此频谱X(k)不可以直接用于画频率响应曲线。为了画图时方便，MATLAB 7.0提供函数fftshift()用于把FFT变换的结果频谱X(k)转换为适合画图显示的格式。对一维信号操作时，fftshift()函数把信号分为左半部分和右半部分，然后交换其左右部分。

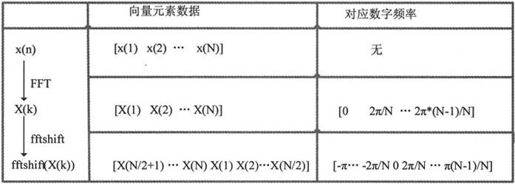
图6-19　N为偶数时fftshift()函数的功能示意图

fftshift()函数不但可以用于一维FFT结果的调整，还可以用于二维FFT甚至多维FFT的调整，其调用格式如下。

·　Y＝fftshift(X)，如果X是向量，交换向量的左部分和右部分；如果X是矩阵，矩阵的第一象限和第三象限交换，第二象限和第四象限交换；

·　Y＝fftshift(X,dim)，在某一维上交换数据的左部分和右部分。

例如，计算单位冲激信号经过一个带阻滤波器前后的频谱，代码设置如下：

由上述程序得到输出如图6-20所示。其中用到滤波器设计的函数butter()，关于该函数的详细内容将在第9章中介绍。

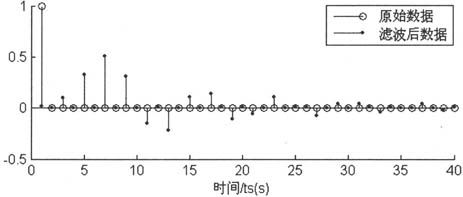
图6-20　单位冲击信号通过带阻滤波器的时域信号

由图6-21可见，单位冲激信号的频谱是一个常数，它通过一个带阻滤波器后的频谱等于带通滤波器的频率响应曲线。这个结果验证了一个信号通过一个线性系统后的频谱等于信号频谱乘以线性系统的频率响应的结论。

2．二维傅立叶变换

在图像处理中经常使用二维傅立叶变换来进行图像滤波等操作。在MATLAB7.0中二维傅立叶变换用函数fft2()来实现。函数fft2()可以看成是对信号进行两次一维傅立叶变换，即fft2(X)＝fft(fft(X).').'。函数fft2()的调用格式如下：。

·　Y＝fft2(X)，X是矩阵，对矩阵X进行二维傅立叶变换；

·　Y＝fft2(X,m,n)，m和n指定傅立叶变换的长度。如果小于该长度则在信号的尾部添加0值；如果大于该长度则截断信号。

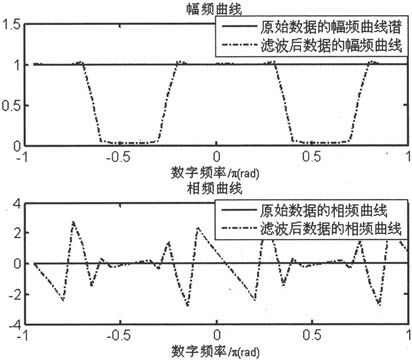
图6-21　单位冲击信号通过带阻滤波器的频域信号

例如，分析图6-22的频谱，代码设置如下：

图6-22　硬币

由上述语句得到图6-22的幅频图，如图6-23所示。

图6-23　幅频图

6.4　功能函数

功能函数就是可以用其他函数作为输入变量的函数，例如一个可以画函数图像的函数fplot()。其调用格式为fplot(@fun,[-pi,pi])。输入变量@fun为需要画成图的函数的函数句柄。MATLAB 7.0的功能函数都在目录“\toolbox\matlab\funfun”下。

6.4.1　函数的表示

在MATLAB 7.0中函数可以用M文件、匿名函数和inline对象来表示。其中匿名函数是MATLAB 7.0的新特性。例如，要表示函数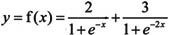

可以通过如下M文件来表示上面的函数：

把customized fun.m文件放在MATLAB 7.0的路径下，例如“\work”目录下，就可以使用该函数了。例如在命令行中输入如下代码：

由上述语句得到输出代码如下：

MATLAB 7.0中也允许使用匿名函数来表示一个函数，例如可以用下面的语句表示上述函数：

由上述语句得到输出代码如下：

在MATLAB 7.0以前的版本中经常使用inline()函数来把一个字符串转换为一个inline对象，该inline对象可以用来表示函数。MATLAB 7.0仍然可以使用inline对象，例如可以用如下的代码表示上述函数：

由上述语句得到的输出结果与使用匿名函数时的输出结果是一样的。有些功能函数还接受使用字符串来表示函数，实际上相当于功能函数内部使用inline()函数把一个字符串转换为inline对象。

6.4.2　函数画图

MATLAB 7.0提供的用于函数画图的函数如表6-6所示。

表6-6　　　　　　函数画图的函数

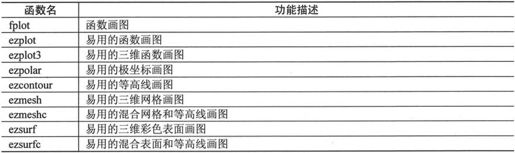
函数画图函数的用法比较简单，而且用法相似。下面就以常用的fplot()函数为例来介绍这些函数的用法。

fplot()的基本调用格式如下。

·　fplot(function,limits)，function为待画图的函数，limits是横坐标数值范围[xmin xmax]，或者是横纵坐标数值范围[xmin xmax ymin ymax]；

·　fplot(function,limits,LineSpec)，LineSpec指定画图的线条属性，与plot()函数的线条属性用法一致；

·　fplot(function,limits,tol)，tol指定画图相对精度，默认值时2e-3；

·　fplot(function,limits,tol,LineSpec)，指定画图的线条属性和画图相对精度；

·　fplot(function,limits,n)，用于指定最少画图点数。函数画图时至少画n＋1个点。默认值是1。

例如，画函数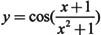在区间[0，10]上的函数图像，代码设置如下：

由上述语句得到结果如图6-24所示的示意图。

6.4.3　函数最小值和零点

求函数最小值和函数的零点是工程上常见的问题，MATLAB 7.0提供一些函数用于解决这类问题。MATLAB 7.0提供的函数如表6-7所示。

表6-7　　　　　　求函数最小值和零点

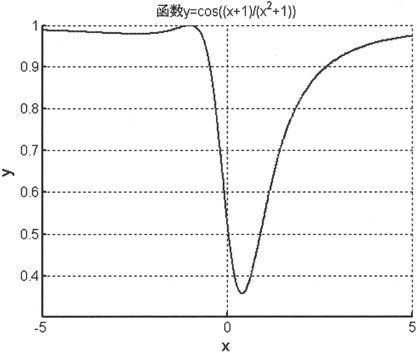
图6-24　函数画图结果

小技巧：如果需要求函数的最大值，只要先把原函数乘上一个-1得到一个新函数，然后求这个新函数的最小值。则新函数最小值的自变量取值与原函数最大值的的自变量取值相同。

1．一元函数最小值

一元函数在给定区间内的最小值问题可以用函数fminbnd()来实现，其调用格式如下。

·　x＝fminbnd(fun,,x1,x2)，在区间[x1 x2]内寻找函数最小值。fun为文件的函数句柄或者匿名函数，x为最小值的自变量取值；

·　x＝fminbnd(fun,x1,x2,options)，使用options选项来指定的优化器的参数。options可以使用函数optimset()来设定；

·　[x,fval]＝fininbnd(…)，多返回一个输出变量最小值fval

注意：函数fminbnd()只能用于连续函数，并且只给出局部最小值。当最小值是在指定区间边界上时，函数收敛的速度很慢。

例如，求正弦函数在[0,10]内的最小值，代码设置如下：

由上述语句得到输出代码如下：

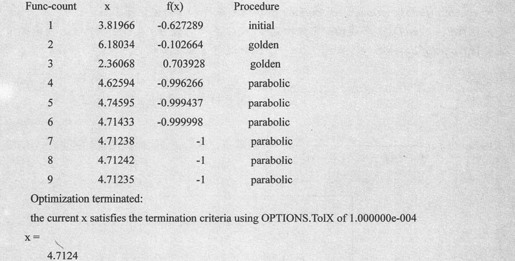
如果要显示计算函数最小值的过程，则可以使用options参数来设定，代码设置如下：

由上述语句得到输出代码如下：

2．求多元函数的最小值

求多元函数的最小值用函数fminsearch()来实现。使用该函数时必须指定开始矢量X0，此函数返回一个在矢量X0附近的局部最小值。其调用格式如下。

·　x＝fminsearch(fun,x0)，在矢量X0附近寻找的局部最小值。fun为M文件的函数句柄或者匿名函数，x为最小值的自变量取值；

·　x＝fminsearch(fun,x0,options)，使用options选项来指定的优化器的参数。options可以使用函数optimset()来设定；

·　[x,fval]＝fininsearch(…)，多返回一个输出变量最小值fval

例如，求二维函数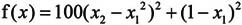的局部最小值，代码设置如下：

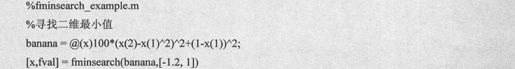
由上述语句得到输出代码如下：

3．求一元函数的零点

可以使用函数fzero()来求一元函数的零点。寻找一元函数零点时，可以指定一个开始点，或者指定一个区间。当指定一个开始点时，此函数在开始点附近寻找一个使函数值变号的区间，如果没有找到这样的区间，则函数返回NaN。如果知道函数零点所在的区间，则可以使用一个包含两个元素的向量来指定此区间。fzero()函数的调用格式如下。

·　x＝fzero(fun,x0)，在x0点附近寻找函数的零点。返回值x是零点的自变量值；

·　x＝fzero(fun,x0,options)，用options参数指定寻找零点的优化器参数；

·　[x,fval]＝fzero(…)，多返回一个输出变量fval，表示函数fun在自变量为x时的函数值；

·　[x,fval,exitflag]＝fzero(…)，多返回一个函数运行返回状态标志。

例如，用函数fzero()来解一元非线性方程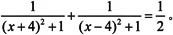该问题等价于求函数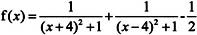的零点，函数f(x)的曲线图形如图6-25所示。

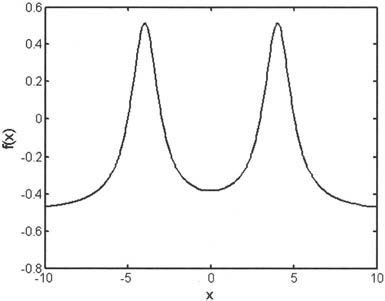
图6-25　函数f(x)的曲线图

求解方程的代码设置如下：

由上述语句得到输出代码如下：

注意：fzero()函数只能返回一个局部零点，不能寻找出所有的零点。此外，fzero()函数的收敛速度与开始点的选取或者区间的选取有关系，尽可能先猜出零点的大概范围，然后在该范围内寻找零点。

4．优化器参数

在求一元函数、多元函数最小值以及求一元函数零点时，都可以设定求优化器的参数。设定优化器参数的函数为optimset()，其调用格式如下：

·　options＝optimset('param1',value1,'param2',value2,…)，用参数名和对用的参数值设定优化器的参数。返回值options是一个结构体；

·　optimset，显示优化器的所有参数名和有效的参数值；

·　options＝optimset，返回一个优化器的结构体，该结构体的所有属性局为空矩阵；

·　options＝optimset(optimfun)，返回求最小值函数optimfun对应的优化器参数；

·　options＝optimset(oldopts,'param1',value1,…)，在原优化器参数oldopts的基础上，改动某些优化器参数；

·　options＝optimset(oldopts,newopts)，用oldopts和newopts组和得到最终的优化器参数。newopts的所有非空参数覆盖oldopts中的值。

函数optimset()中常用的优化器参数如表6-8所示。

表6-8　　　　　　　优化器参数

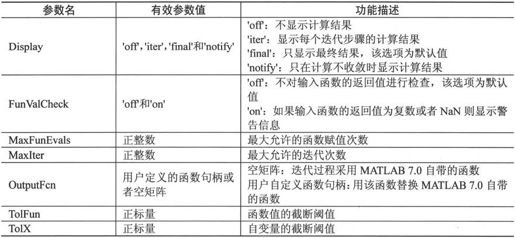
如果要得到最小优化器的参数，则可以使用函数optimget()，其调用格式如下：

·　val＝optimget(options,'param')，返回最小优化器参数'param'的值；

·　val＝optimget(options,'param',default)，返回最小优化器参数'param'的值，如果该值为空则返回default。

6.4.4　数值积分

MATLAB 7.0提供的数值积分函数如表6-9所示。

表6-9　　　　　　数值积分函数

1．一元函数的数值积分

MATLAB 7.0提供了两个函数quad()和quad1()计算一元函数的积分。函数quad()采用低阶的自适应递归Simpson方法，函数quad1()则采用高阶的自适应Lobatto方法。函数quad()函数的调用格式如下：

·　q＝quad(fun,a,b)，计算函数fun在[a b]区间内的定积分。fun为函数句柄，a和b都是标量，它们分别是积分区间的下界和上界；

·　q＝quad(fun,a,b,tol)，以绝对误差容限tol计算函数fun在[a b]区间内的定积分，取代MATLAB 7.0中默认的绝对误差容限值10^-6；

·　q＝quad(fun,a,b,tol,trace)，当trace为非零值时，显示计算定积分的迭代过程中向量[fcnt a b-a Q]的值；

·　[q,fcnt]＝quad1(fun,a,b,…)，多返回一个输出变量fcnt，表示计算定积分过程中计算函数值的次数。

例如，求归一化高斯函数的在区间[-1 1]上的定积分，代码设置如下：

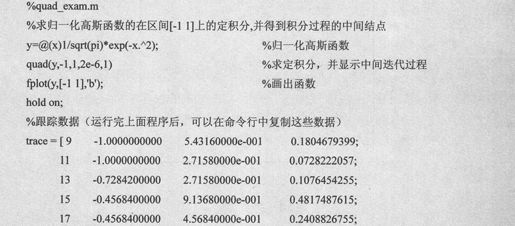
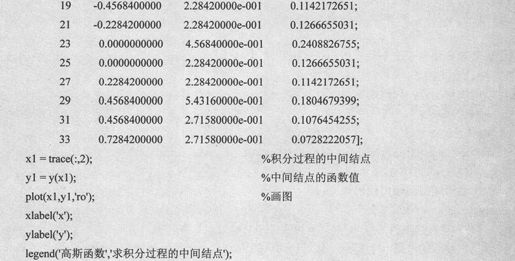
由上述语句得到输出代码如下：

积分过程如图6-26所示。

函数quad1()的调用格式与函数quad()相同，可以参见上面quad()函数的用法。

在一维积分的过程中，有可能得到3种警告信息：

·　'Minimum step size reached'，已经达到了最小步长。这意味着积分的迭代区间比给定的定积分区间的截断误差值小。一般来说，这表明被积函数的可积性是奇异的；

·　'Maximum function count exceeded'，计算函数值的次数超过10000，一般来说，这表明被积函数的可积性是奇异的；

·　'Infinite or Not-a-Number function value encountered'，积分过程中出现浮点数溢出或者被0除。

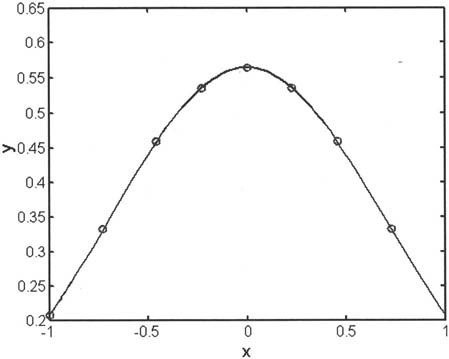
图6-26　积分过程

2．矢量积分

矢量积分相当于多个一元定积分，例如求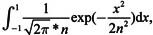n＝1,2,3,4,5就可以用矢量积分，代码设置如下：

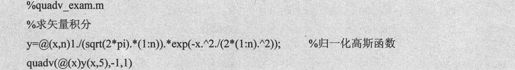
由上述语句得到输出代码如下：

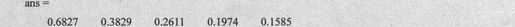
矢量积分的结果是一个向量，其每一元素的值为一个一元函数定积分的值。

3．二重和三重积分

二重积分的形式如下：

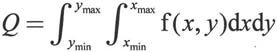
MATLAB 7.0中使用函数dblquad()来计算二重积分。该函数先计算内积分值，然后利用内积分的中间结果来计算二重积分。根据dxdy的顺序，称x为内积分变量，y为外积分变量。函数dblquad()的基本格式如下：

·　q＝dblquad(fun,xmin,xmax,ymin,ymax)，计算二元函数fun在矩形区域[xmin,xmax,ymin,ymax]上的二重积分。fun为函数句柄，xmin、ymin、xmax和ymax都是标量，它们分别是积分区间的下界和上界；

·　q＝dblquad(fun,xmin,xmax,ymin,ymax,tol)，用tol指定绝对计算精度；

·　q＝dblquad(fun,xmin,xmax,ymin,ymax,tol,method)，用method指定计算一维积分时采用的函数。MATLAB 7.0默认采用函数quad()来计算一维积分，可以设method＝@quad1，从而采用函数quad1()来计算一维积分。用户还可以编写自己的一维积分函数以用于计算二维积分，该函数的调用格式必须与函数quad()一致。

例如，计算二维高斯函数在矩形区间[-1 1 -1 1]上的二重积分，代码设置如下：

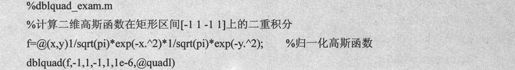
由上述语句得到输出代码如下：

函数dblquad()处理的都是矩形积分区域。若要计算非矩形的积分区间的二重积分，可以用一个大的矩形积分区域包含非矩形的积分区间，然后在非矩形的积分区间之外的区域上把二元函数的值取零。

例如，计算二维高斯函数在圆形区域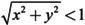上的二重积分，代码设置如下：

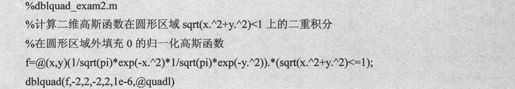
由上述语句得到输出代码如下：

三重积分的的形式如下：

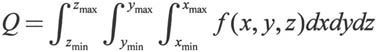
三重积分可以用函数triplequad()来实现，其用法与二重积分类似。

6.4.5　在功能函数中使用含参函数

在很多情况下，例如要求不同a和b情况下，计算函数f(x)＝e^x＋a*x－b的零点。这时在功能函数中就要使用含参函数，它有两种方法：使用嵌套函数和使用匿名函数。

1．用嵌套函数提供函数参数

一个使用含参函数的方法是编写一个M文件，该文件首先把含参函数的参数当作输入，然后调用功能函数来处理含参函数，最后把含参函数以嵌套函数的方式包含在M文件中。例如，求函数f(x)＝e^x＋a*x－b的零点，代码设置如下：

例如求a＝1,b＝[-10 10]时，含参函数的零点取值随着参数b变化的关系，可以通过如下程序来实现：

由上述语句得到如图6-27所示的示意图。

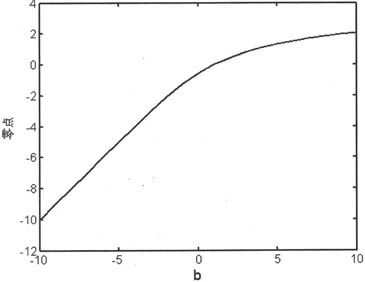
图6-27　零点轨迹

2．用匿名函数提供函数参数

使用含参函数还可以利通过匿名函数来实现。由于与函数fzero()一样，一般功能函数只接受一个自变量，因此函数的参数在使用之前必须先赋值。具体步骤如下：

·　首先创建一个含参函数，保存为M文件格式。函数输入为自变量x以及函数参数；

·　在调用功能函数的M文件中给参数赋值；

·　用含参函数创建匿名函数；

·　把匿名函数句柄传递给功能函数计算。

例如，用匿名函数来实现上小节的例子，首先建立含参函数，其代码设置如下：

然后，用如下代码来实现计算函数零点：

由上述语句得到的输出图形与图6-27是一致的。

6.5　微分方程组数值解

在MATLAB 7.0中可以计算3类微分方程数值解问题，即常微分方程组的初值问题、延迟微分方组和常微分方程组的边界问题。

6.5.1　常微分方程组的初值问题

MATLAB 7.0可以解决3种常微分方程组的初值问题，即显式常微分方程组、线性隐式常微分方程组和完全隐式常微分组。显式常微分方程组的初值问题的形式如下：

其中y',y和y₀为向量，故可以代表常微分方程组。显式常微分方程组的初值问题即已知常微分方程的初值y(0)，求y随时间的变化y(t)。

线性隐式常微分方程组可以表述为如下形式：

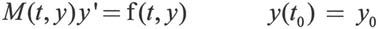
该形式也称为加权常微分方程组。

完全隐式常微分组可以表述为为如下形式：

以上介绍的都是一阶常微分方程组问题，如果遇到高阶常微分方程则可以先把高阶常微分方程转换为一阶常微分方程组。一个任意的高阶常微分方程可以表述如下：

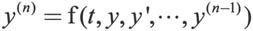
上式可以化为如下一阶常微分方程组：

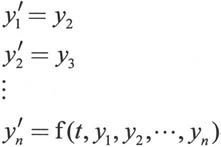
1．显式常微分方程组的解法

由于显式常微分方程组的多样性，需要根据显式常微分方程组的特点采用相应的解法来处理。MATLAB 7.0给出7种解法，分别由7个不同的函数来实现，它们是函数ode45()、ode23(),ode113()、ode15s()、ode23s()、ode23t()和ode23tb()。

在介绍这些函数之前，首先介绍一个概念——刚性（stiffness）。定性地讲，对一个常微分方程组，如果其Jocabian矩阵的特征值相差十分悬殊，那么这个方程组就称为刚性方程组。对于刚性方程组，为了保持解法的稳定，步长选取很困难。有些解法不能用于解刚性方程组，而有些解法对方程组的刚性要求不严，可以用于解刚性问题。表6-10对MATLAB 7.0中的7个解法进行了对比。

表6-10　　　　　　常微分方程组解法对比

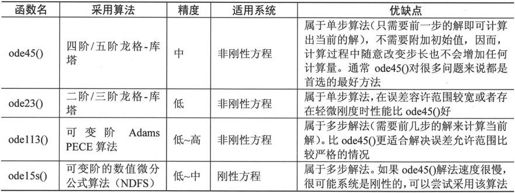
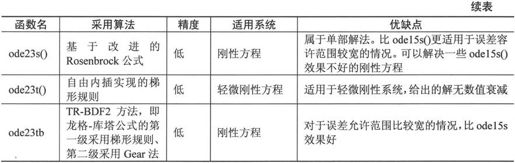
解显式常微分方程的7个函数的调用格式是完全一样的，下面以函数ode45()为例来说明它们的基本调用格式：

·　[t,Y]＝ode45(odefun,tspan,y0)，odefun为代表常微分方程的方程组，其格式为y'＝f(t,y)，其中t是一个标量，y是一个列向量，y'是与y具有相同长度的列向量。tspan可以是两个元素的向量[t0 tf］，这时函数返回t0到tf时间范围内的常微分方程的解；tspan也可以是[t0,t1,…,tf］，这时函数返回在时间[t0,t1,…,tf］上的常微分方程的解。y0是y具有相同长度的列向量，用于指定初始值；

·　[t,Y]＝ode45(odefun,tspan,y0,options)，options参数用于设定微分方程解法器的参数。

options可以由函数odeset()来获得。

例如，求非刚性方程y″－µ(1－y²)y′＋y＝0，其中μ是参数，在本例中μ＝1。首先是要把该二阶常微分方程改写为一阶常微分方程组：

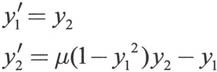
然后，把该一阶常微分方程组用一个M文件形式的函数来表述，代码设置如下：

注意：表示一个微分方程的函数必须有时间t这个输入变量，然而在函数内部计算时可以不使用t这个变量。

最后，用函数ode45()来解这微分方程，并画图计算结果，代码设置如下：

由上述语句得到如图6-28所示的示意图。

如果要处理含参数的微分方程组可以把参数作为表示微分方程组的函数的第3个输入变量。然后再调用函数ode45()时，把参数值作为最后一个输入变量。其微分方程组可以表示为：

如果要求参数u＝10的微分方程组，可以用如下代码实现：

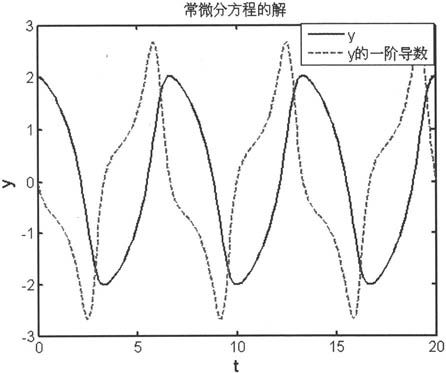
图6-28　常微分方程解

2．设置常微分方程组解法器参数

正如上小节介绍的，在调用常微分方程组函数时可以输入一个options结构体，从而设置解法器的参数。该options结构体可以用函数odeset()来设定，其调用格式如下：

·　options＝odeset('name1',value1,'name2',value2,…)，用参数名和参数值对来设定解法器的参数；

·　options＝odeset(oldopts,'name1',value1,…)，修改原来的解法器options结构体oldopts，只改变指定的某些参数的值；

·　options＝odeset(oldopts,newopts)，合并两个解法器options结构体oldopts和newopts，这两个结构体中值不同的参数，采用newopts中的参数值；

·　odeset，显示所有的参数值和它们的默认值。

常微分方程组解法器参数如表6-11所示。

表6-11　　　　　　常微分方程组解法器参数

例如，设置解法器的输出函数为二维相位平面画图，代码设置如下：

由上述语句得到如图6-29所示的示意图。

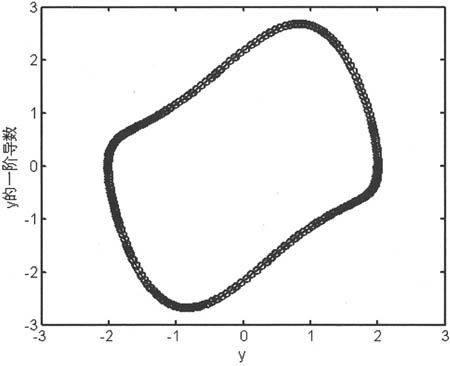
6-29　二维相位平面画图

3．线性隐式常微分方程组

线性隐式常微分方程组可以利用ode类函数的解法器参数options来解决。首先创建M文件函数来表示加权函数M(t,y)，然后用odeset()函数来把加权函数设置到解法器的Mass参数中，最后用ode类函数来解微分方程组。

例如，求解线性隐式常微分方程组(y＋1)y'＝y²＋2y－2，首先创建表示微分方程的函数f(t,y)和M(t,y)，表示f(t,y)的函数，代码设置如下：

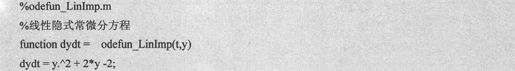
表示M(t,y)的函数，代码设置如下：

求解微分方程，代码设置如下：

由上述语句得到如图6-30所示的示意图。

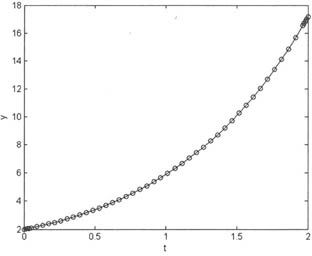
图6-30　线性隐式常微分方程的解

4．完全隐式常微分方程组

MATLAB 7.0的新特性之一是提供了一个完全隐式常微分方程组的解法器ode15i()。其调用格式如下：

·　[t,Y]＝ode15i(odefun,tspan,y0,yp0)，odefun是代表完全隐式常微分方程组的函数，其形式为f(t,y,y')。tspan可以是两个元素的向量[t0 tf］，这时函数返回t0到tf时间范围内的常微分方程的解；tspan也可以是[t0,t1,…,tf]，这时函数返回在时间[t0,t1,…,tf]上的常微分方程的解。y0和yp0用于指定微分方程的初始值，初始值必须是自洽的，即满足f(t,y0,yp0)＝0；

·　[t,Y]＝ode15i(odefun,tspan,y0,yp0,options)，用options结构体设定解法器的参数，options结构体可以由函数odeset()来得到。

处理完全隐式常微分方程组的一个重要问题是如何得到自洽的初始值。MATLAB 7.0提供函数decic()来得到自洽的初始值。其调用格式如下：

·　[y0mod,yp0mod]＝decic(odefun,t0,y0,fixed_y0,yp0,fixed_yp0)，odefun是代表完全隐式常微分组的函数。t0值为初始时间，y0和yp0是猜测的初始值。函数decic()会通过不断改变初始值，最终得到自洽的初始值。如果希望在改变初始值的过程中保持某一个分量不变，可以通过fixed_y0输入来实现。当fixed_y0(i)＝1时，y0(i)不会被改变。fixed_yp0的作用与fixed_y0是一样的；

·　[y0mod,yp0mod]＝decic(odefun,t0,y0,fixed_y0,yp0,fixed_yp0,options)，用options结构体设定解法器的参数，options结构体可以由函数odeset()来得到。

例如，解完全隐式常微分方程Weissinger方程，其形式如下：

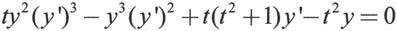
当初值等于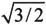时，方程的解析解为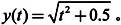本例将用数值解法来求解这个问题。首先创建一个代表该方程的M文件函数，代码设置如下：

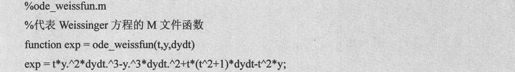
解微分方程的程序，代码设置如下：

由上述语句得到如图6-31所示的示意图。

6.5.2　延迟微分方程组数值解

延迟微分组方程的形式如下：

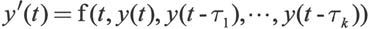
在MATLAB 7.0中使用函数dde23()来解延迟微分方程。其调用格式如下：

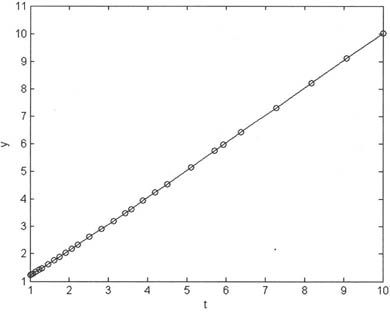
图6-31　完全隐式常微分方程解

·　Sol＝dde23(ddefun,lags,history,tspan)，其中ddefun是代表延迟微分方程的M文件函数，ddefun的格式为dydt＝ddefun(t,y,Z)，t是当前时间值，y是列向量，Z(:,j)代表y(t－T_k)，而T_k值在第二个输入变量lags(k)中存储。history为y在时间t0之前的值，可以有3种方式来指定history。第1种是用一个函数y(t)来指定y在时间t0之前的值；第2种方法是用一个常数向量来指定y在时间t0之前的值，这时y在时间t0之前的值被认为是常量；第3种以前一时刻的方程解sol来指定时间t0之前的值。tspan是两个元素的向量[t0 tf]，这时函数返回t0～tf时间范围内的延迟微分方程组的解；

·　Sol＝dde23(ddefun,lags,history,tspan,option)，option结构体用于设置解法器的参数，option结构体可以由函数ddeset()来获得。

函数dde23()的返回值是一个结构体，它有7个属性，其中重要的属性有如下5个：

·　sol.x，dde23选择计算的时间点；

·　sol.y，在时间点x上的解y(x)；

·　sol.yp，在时间点x上的解的一阶导数y'(x)；

·　sol.history，方程初始值；

·　sol.solver，解法器的名字'dde23'。

其他两个属性为so1.stat和so1.discont。

如果需要得到在[t0 tf]之间tint时刻的解，可以使用函数deval，其用法为：yint＝deval(sol,tint)，yint是在tint时刻的解。

例如，求解如下延迟微分方程组：

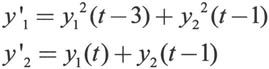
初始值为：

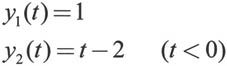
首先，确定延迟向量lags，在本例中lags＝[1 3]。

其次，创建一个M文件形式的函数表示延迟微分方程组，代码设置如下：

然后，创建一个M文件形式的函数表示延迟微分方程组的初始值，代码设置如下：

最后，用dde23解延迟微分方程组和用图形显示解，代码设置如下：

由上述语句得到如图6-32所示的示意图。

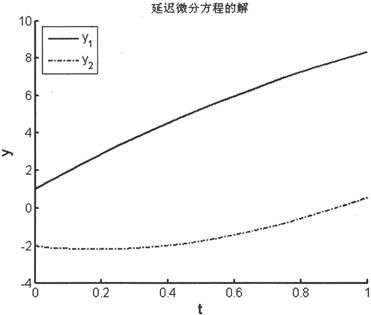
图6-32　延迟微分方程组的解

6.5.3　常微分方程组的边界问题

常微分方程组的边界问题的形式如下：

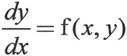
同时要指定函数y(x)在某些边界条件下的值，然后在边界条件下求函数y(x)，其中x是独立变量。MATLAB 7.0中使用函数bvp4c()来处理常微分方程组的边界问题。该函数解决第一类边界条件问题，即边界条件是：

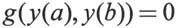
其中a和b是求解区间的下界和上界，即要求解出y在区间[a b]上的值。

常微分方程组的边界问题与常微分方程组的初值问题的不同之处在于：常微分方程组的初值问题总是有解的，然而常微分方程组的边界问题有时会出现无解的情况，有时会出现有限个解，有时会出现无穷多个解。因此在解常微分方程组的边界问题时，不可或缺的一部分工作是提供猜测解。猜测解决定了解边界问题的算法性能，甚至算法是否成功。

在边界问题中，还经常出现附加的未知参数，其方程形式如下：

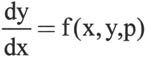
其边界条件为：

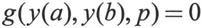
在这种情况下，边界条件必须充分，从而能够决定未知参数p。

函数bvp4c()的调用格式如下：

·　Sol＝bvp4c(odefun,bcfun,solinit)，odefun是描述常微分方程组的函数，其格式为dydx＝odefun(x,y)，或者包含未知参数dydx＝odefun(x,y,parameters)。bcfun是描述边界条件的函数，其格式为res＝bcfun(ya,yb)，或者包含未知参数res＝bcfun(ya,yb,parameters)。solinit是对方程解的猜测解，它是一个结构体，包含x、y和parameters3种属性。solinit必须满足solinit.x(1)＝a和solint.x(end)＝b，parameters是对未知参数的一个猜测解。solinit可以由函数bvpinit()得到；

·　sol＝bvp4c(odefun,bcfun,solinit,options)，使用options结构体来设定解法器的参数。options结构体可以由函数bvpset()得到。

边界问题的猜测解可以由函数solinit()得到，其调用格式如下：

·　solinit＝bvpinit(x,yinit)，x是猜测解的自变量x取值，yinit猜测解的因变量y取值。如果需要在区间[a b]上求解方程，x取linspace(a,b,10)就足够了，在解变化比较快的时候，需要用长的自变量x；

·　solinit＝bvpinit(x,yinit,parameters)，parameters未知参数的猜测解。

例如，求Mathieu方程的特征值。Mathieu方程的形式为：

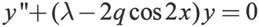
其中q-1是Mathieu方程的阶数，为已知参数。λ是未知参数Mathieu方程的特征值。为在本例中q＝5，即求4阶Mathieu方程的特征值λ。首先把方程改写成一阶常微分方程的形式：

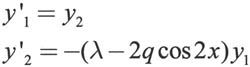
指定边界条件为：

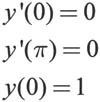
其次，创建M文件来描述Mathieu方程，代码设置如下：

然后，创建M文件来描述方程的初值，代码设置如下：

还需要，创建M文件来描述方程的边界条件，代码设置如下：

最后，用函数bvp4c来解方程，并画图显示结果，代码设置如下：

由上述语句得到如图6-33所示的示意图。

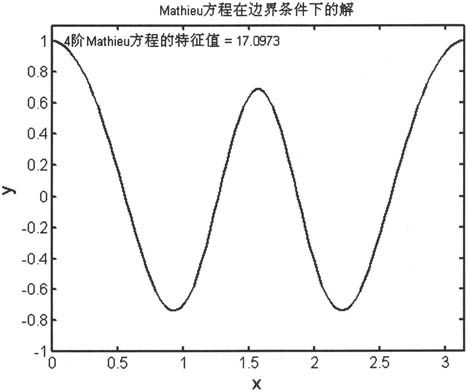
图6-33　Mathieu方程在边界条件下的解