第10章　信号处理工具箱

MATLAB的推出得到了各个领域专家学者的关注，其强大的扩展功能为各个领域的应用提供了基础，相继推出了各种MATLAB工具箱，为各个层次的研究人员提供了有力的工具，节省了时间。本章将介绍信号处理（signal processing）工具箱的使用。

10.1　数字信号处理基本理论

在计算机中，所有的信号都是离散信号，因此在使用MATLAB进行信号处理之前，首先要了解离散时间信号处理的相关理论。

10.1.1　离散信号与系统

1．离散信号

信号是信息的表现形式，是通信传输的客观对象，其特性可以从两个方面来描述，即时间特性和频率特性。信号之所以不同是因为各自有不同的时间特性和频率特性，并且两者之间有一定的对应关系。若t是定义在时间轴上的离散点，则x(t)为离散时间信号，表示为x(nT)，T表示相邻两个点之间的时间间隔，也称为抽样周期，n取整数并代表时间的离散时刻。一般可以把T归一化为1，这样x(nT)可简记为x(n)，又称为离散时间序列。

在MATLAB中，可用一个向量来表示一个有限长度的序列（由于内存的限制，不可能表示一个任意无限序列），示例代码设置如下：

MATLAB对下标的约定从1开始递增，如果要包含采样时刻的信息，则需要两个向量来表示，对于上面的序列应有：

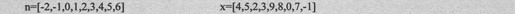
为了分析的方便，数字信号处理理论中定义了一些基本的典型的序列，其定义和MATLAB表达式如下：

·　单位取样序列

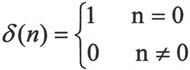
该表达式可利用zeros函数或者逻辑关系来实现，代码设置：

或者可以写成：

·　单位阶跃序列

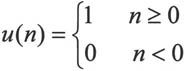
该表达式可利用ones函数来实现，代码设置如下：

·　实指数序列

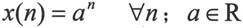
该表达式通过MATLAB实现，代码设置如下：

·　复指数序列

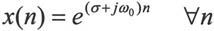
该表达式通过MATLAB实现，代码设置如下：

·　正（余）弦序列

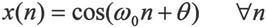
该表达式通过MATLAB实现，代码设置如下：

·　随机序列

在MATLAB中提供了两类（伪）随机信号：

rand(1,N)产生[0,1]上均匀分布的随机矢量；randn(1,N)产生均值为0，方差为1的高斯随机序列。其他分布的随机数可通过上述随机数的变换而产生。

·　周期序列

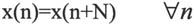
2．离散系统

系统是由若干相互作用和相互依赖的事物组合而成的并具有特定功能的整体。系统分析的着眼点是分析系统的输入和输出的关系，而不涉及系统的内部情况。

一个离散系统可以抽象为一种变换或者一种映射，即y(n)＝T[x(n)]。其中T代表变换。在数字信号处理中，所研究的系统基本上都是线性时不变系统（LSI系统），其输入／输出关系可以通过冲激响应h(n)表示：

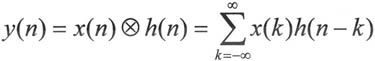
其中x(n)和h(n)作卷积运算，MATLAB提供了求卷积函数conv。有关线性时不变系统中涉及的重要概念，比如稳定性、因果性和移不变性等可参看信号与系统的经典教材。

10.1.2　Z变换

Z变换是离散系统和离散信号分析、综合的重要工具，其地位和作用如同拉普拉斯变换之于连续信号和系统。

1．Z变换的定义

给定离散信号x(n)，其Z变换的定义为：

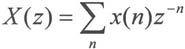
其中z为复变量。如果n的取值范围为-∞～+∞，则上式定义的Z变换称为双边Z变换，如果n的取值范围为0～+∞，则上式称为单边Z变换。实际的物理系统的抽样响应h(n)在n＜0时恒为0，因此对应的都是单边Z变换。

X(z)存在的z的集合称为收敛域（ROC），即满足下式：

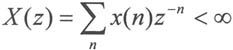
ROC由|z|决定，因此一般为环形。序列在单位圆上的Z变换就是序列的傅立叶变换，若x(n)＝h(n)，则该变换就是系统的频率响应。

2．Z变换的性质

·　线性

若Z[x₁(n)]＝X₁(z)，ROC:R₁；Z[x₂(n)]＝X₂(z)，ROC:R₂。则有：

Z[ax₁(n)＋bx₂(n)]＝aX₁(z)＋bX₂(z)，ROC为R₁和R₂的公共部分。

·　时移性质

Z[x(n－k)]＝z^-kX(z)，ROC不变。

·　频移性质

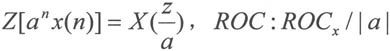
·　折叠

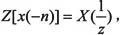ROC:与ROC_x相反，即ROC_x的逆。

·　复共轭

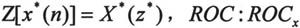
·　Z域微分

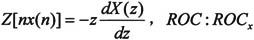
·　序列相乘

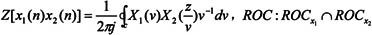的逆，其中C为公共ROC中包围原点的闭合围线。

·　序列卷积

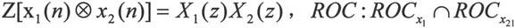
10.1.3　离散傅立叶变换

Z变换提供了任意序列在频域的表示方法，但它是连续变量z的函数，因此无法直接利用计算机进行数值计算。为了使用MATLAB，必须截断序列，得到有限个点的表达式。这就产生了离散傅立叶级数（DFS）、离散傅立叶变换（DFT）和计算量小的快速傅立叶变换（FFT）。

如果信号在频域上是离散的，则该信号在时域上就是周期性的函数。反之在时域上离散的信号在频域上必然表现为周期性的频率函数。可以得出一个一般规律：一个域的离散必然造成另一个域的周期延拓。这种离散变换，本质上都是周期的。因此，首先从周期序列及其傅立叶级数开始讨论，然后再讨论可作为周期序列一个周期的、有限长序列的离散傅立叶变换（DFT）。

1．离散傅立叶级数（DFS）

对于周期为N的离散时间信号序列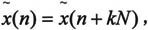其中k为任意整数，由于在Z平面上没有任何收敛区域，所以不能进行Z变换，但是可以用傅立叶级数来表达，其基波频率为2π/N，用复指数表示为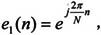第k次谐波为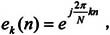所以有e_k＋N(n)＝e_k(n)，可得离散傅立叶级数公式如下：

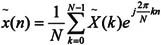
在上式中求和号前所乘的系数1/N是习惯上采用的常数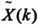，是k次谐波的系数：

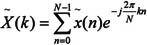
习惯上也常采用符号W_N＝e^-j(2π／N)，这样离散傅立叶级数对可以表示为：

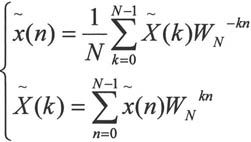
2．离散傅立叶变换（DFT）

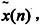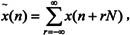周期序列实际上只有有限个序列值有意义，因此它的许多特性可以沿用到有限长序列上，对于一个长度为N的有限长序列x(n)，以x(n)为主值序列并以N为周期进行延拓得到周期序列即当0≤n≤N-1时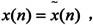，n为其余值时x(n)为0。

由离散傅立叶级数公式，可以得到有限长序列x(n)的离散傅立叶变换公式：

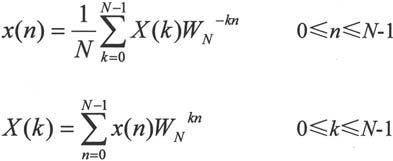
离散傅立叶级数和离散傅立叶变换与Z变换有类似的性质，详细的介绍可以参照信号与系统教材，本节不再赘述。

3．快速傅立叶变换（FFT）

快速傅立叶变换是离散傅立叶变换的快速算法，其应用极大地推动了DSP理论和技术的发展。下面介绍FFT的基本思想和实现。

·　FFT的基本思想

N点序列的DFT为

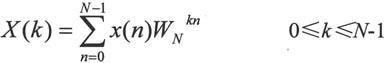
由于系数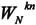是一个周期函数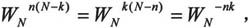：且是对称的：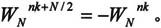

FFT正是基于这样的基本思想而发展起来的。

·　FFT的实现方法

FFT的算法形式有很多种，但基本上可以分为两大类：时间抽取法（DIT-FFT）和频率抽取法（DIF-FFT）。这两种算法在思想上基本一致，只是划分方式略有差异，这里仅以DIT-FFT为例进行说明。

当N是2的整数次方时，称为基2的FFT算法。

首先将序列x(n)分解为两组，偶数项为一组，奇数项为一组：

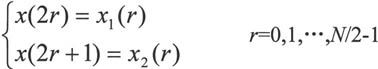
将两组分别进行N／2点的DFT可得：

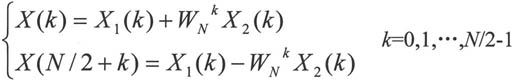
重复这一过程，可得到x(n)的FFT，整个运算需要次复数乘法和Nlog₂N次复数加法。

在MATLAB中，可直接利用内部函数fft进行计算，速度比较快，有关其具体用法在本章的第3节会给出例子。

10.1.4　数字滤波器结构

数字信号处理的目的之一是设计某种设备或建立某种算法用以处理序列，使序列具有某种确定的性质，这种设备或算法结构就称为数字滤波器。数字滤波器可以分为有限冲激响应（FIR）和无限冲激响应（IIR）两种。滤波器的设计结果受滤波器的类型和结构的影响。本节分别介绍这两种滤波器的结构。

1．IIR滤波器

IIR滤波器的系统函数为：

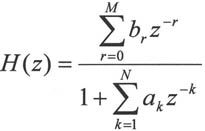
其差分方程可表示为：

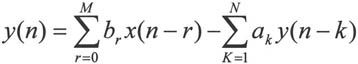
由其系统函数或差分方程可知，实现IIR滤波器有直接型、级联型和并联型三种结构。

·　直接型

直接型分为直接Ⅰ型和直接Ⅱ型两种，直接Ⅰ型可由差分方程得到，第一部分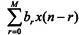表示将输入信号进行延时，组成M节的延时网络，把每节延时抽头与常系数相乘，再把结果相加，这是一个横向结构网络，即实现零点的网络，第二部分表示将信号输出延时，组成N节的延时网络，把每节延时抽头后与常系数相乘，然后再把结果相加，由于这部分是对输出的延时，故为反馈网络，这部分网络实现极点。y(n)的信号流图如图10-1所示。

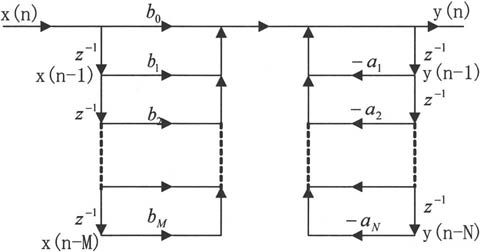
图10-1　直接Ⅰ型

直接Ⅱ型可以由系统函数得到，将分子和分母的倒数分别看作一个网络，则整个系统可看作是这两个网络的级联，如图10-2所示。

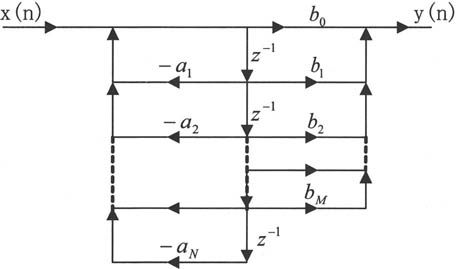
图10-2　直接Ⅱ型

直接Ⅱ型结构比直接Ⅰ型速度快且经济（延时单元少一半），但它们的系数都不能直接控制滤波器特性，对字长效应敏感。

在MATLAB中，可以DSP工具函数filter实现IIR的直接形式。

·　级联型

对IIR滤波器系统函数进行因式分解，若a_k，b_r均为实数，则零点和极点只有实数和共轭复数，合并共轭因子有如下的表达式：

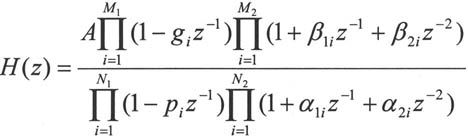
将单实根视为二阶因子的特例，设M≤N，则：

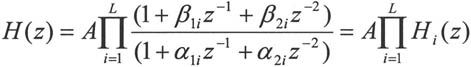
其中，L表示(N＋1)／2中的最大整数。H_i(z)称为二阶基本节，可以采用直接Ⅱ型实现，H(z)则由H_i(z)级联而成，级联型的具体体现形式如图10-3所示。

图10-3　级联型

在MATLAB中，给定直接形式滤波器的系数，可计算出级联形式的系数，这可由扩展函数dir2cas实现，然后利用扩展函数casfiltr实现滤波器的级联形式。

·　并联型

作为系统函数的另一种表示形式，可以将H(z)表示如下形式的部分分式展开：

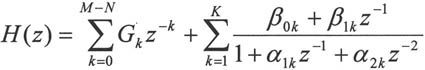
其中K＝N／2，每一部分均为二阶，它们之间是并联关系，M＝N＝4为例，画出其结构图如图10-4所示。

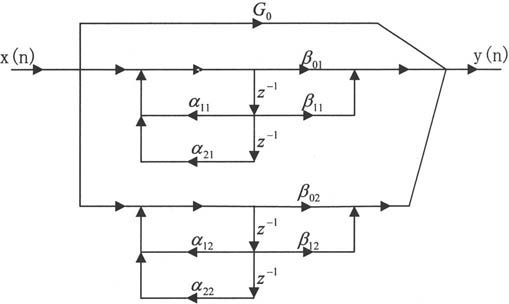
图10-4　并联型

在MATLAB下，已经设计了将滤波器直接形式转化为并联形式的扩展函数dir2par，其中用到了复共轭对比较函数cplxcomp，这样就可利用parfiltr函数实现滤波器的并联形式。

2．FIR滤波器

有限冲激响应（FIR）滤波器的系统函数为：

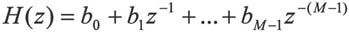
差分方程表示为：

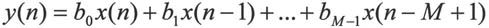
与IIR滤波器相比，FIR滤波器结构相对简单，而且可以设计成线性相位。实现FIR滤波器可采用直接形式、级联形式、线性相位形式和频率取样形式四种结构。

·　直接形式

与IIR类似，以M＝5为例，结构如图10-5所示，在MATLAB中可通过filter函数实现。

图10-5　FIR滤波器的直接形式

·　级联形式

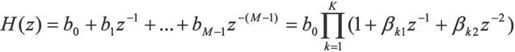
其中，K＝M／2，以M＝7为例，其结构如图10-6所示。

图10-6　FIR滤波器级联形式

在MATLAB中，可采用dir2cas和casfiltr来实现。

·　线性相位形式

线性相位条件∠H(e^jω）＝β－αω，-π＜ω≤π，其中β＝0或±π／2，α为常数。对H(z)则有下列对称性：

h(n)＝h(M－1－n)　β＝0，0≤n≤M－1　　（对称冲激响应）

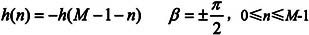（反对称冲激响应）

以M为7（代表奇数）和M为6（代表偶数）为例，对称型的结构如图10-7所示。

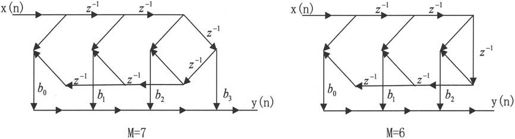
图10-7　FIR滤波器线性相位形式

在MATLAB中，实现FIR线性相位形式的函数等同于直接形式，可用filter函数。

·　频率取样形式

冲激响应h(n)的M点DFT为H(k)（0≤k≤M－1），则有H(z)＝Z[h(n)]＝Z[IDFT(H(k))]利用内插公式可得：

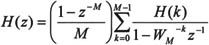
这表明在这种结构中采用了离散傅立叶变换H(k)，而不是冲激响应h(n)。这种结构分成两部分，以M取4为例，频率取样形式如图10-8所示。

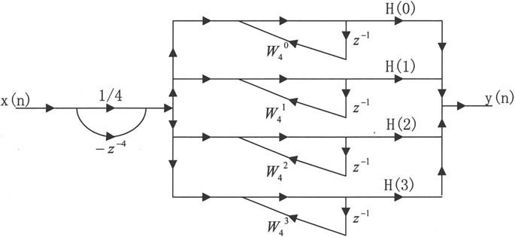
图10-8　FIR滤波器频率取样形式

在MATLAB中，给定h(n)或H(k)，则可借助于扩展函数dir2fs得到频率取样形式，它将h(n)值转换为频率取样形式。

此外还有一种广泛应用的格形滤波器结构，可参阅有关文献。在第3节中将具体讨论这些滤波器基于MATLAB的实现方法。

10.2　MATLAB 7.0的信号处理工具箱函数

MATLAB包含了进行信号处理的许多工具箱函数，有关这些工具箱函数的使用可通过Help命令得到。为使用方便，本节将按分组给出这些函数的简单说明，在后面的章节会给出其中一部分函数的使用举例。详细的文档可以在Help目录下找到。

10.2.1　波形产生（Waveform Generation）

在该工具箱里包含以下几个函数：

·　chirp：产生扫频余弦函数；

·　diric：产生Dirichlet或周期sinc函数；

·　gauspuls：产生高斯调制的正弦曲线脉冲；

·　gmonopuls：产生高斯单脉冲；

·　pulstran：产生一个脉冲序列；

·　rectpuls：产生一个非周期的抽样方波；

·　sawtooth：产生锯齿波或三角波；

·　sinc：产生sinc函数，即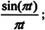

·　square：产生方波；

·　tripuls：产生一个非周期的采样三角波；

·　vco：压控振荡器。

10.2.2　滤波器分析（Filter Analysis）

在该工具箱里包含以下几个函数：

·　abs：求绝对值（幅值，这是一个MATLAB函数）；

·　angle：求相角（这是一个MATLAB函数）；

·　freqs：模拟滤波器的频率响应；

·　freqspace：频率响应中的频率间隔（这是一个MATLAB函数）；

·　freqz：计算数字滤波器的频率响应；

·　fvtool：打开滤波器可视化工具；

·　grpdelay：计算平均滤波器延迟（群延迟）；

·　impz：计算数字滤波器的冲激响应；

·　phasedelay：计算数字滤波器的相位延迟响应；

·　phasez：计算数字滤波器的相位响应；

·　Stepz：计算数字滤波器的阶跃响应；

·　unwrap：展开相角（这是一个MATLAB函数）；

·　zerophase：计算数字滤波器的零相位响应；

·　zplane：离散系统零极点图。

10.2.3　滤波器实现（Filter Implementation）

在该工具箱里包含以下几个函数：

·　conv：求卷积和多项式乘法（这是一个MATLAB函数）；

·　conv2：二维卷积（这是一个MATLAB函数）；

·　convmtx：卷积矩阵；

·　deconv：反卷积和多项式除法（这是一个MATLAB函数）；

·　fftfilt：采用重叠相加法基于FFT的FIR滤波器实现；

·　filter：直接滤波器实现（这是一个MATLAB函数）；

·　filter2：二维数字滤波（这是一个MATLAB函数）；

·　filtfilt：零相位数字滤波；

·　filtic：直接II型滤波器的初始条件选择；

·　latcfilt：格型和格-梯型滤波器实现；

·　medfilt1：一维中值滤波；

·　sgolayfilt：Savitzky-Golay滤波；

·　sosfilt：二阶（四次）IIR数字滤波；

·　upfirdn：过采样，FIR滤波和抽样。

10.2.4　线性系统变换（Linear System Transformations）

在该工具箱里包含以下几个函数：

·　latc2tf：将格形滤波器参数转换维传输函数格式；

·　polystab：稳定多项式；

·　polyscale：多项式的根的数值范围；

·　residuez：Z变换部分分式展开或留数计算；

·　sos2ss：变系统二阶分割形式为状态空间形式；

·　sos2tf：变系统二阶分割形式为传递函数形式；

·　sos2zp：变系统二阶分割形式为零极点增益形式；

·　ss2sos：变系统状态空间形式为二阶分割形式；

·　ss2tf：变系统状态空间形式为传递函数形式；

·　ss2zp：变系统状态空间形式为零极点增益形式；

·　tf2latc：变传递参数形式为格形滤波器形式；

·　tf2sos：变传递函数形式为系统二阶分割形式；

·　tf2ss：变传递函数形式为系统状态空间形式；

·　tf2zp：变连续时间传递函数为零极点增益形式；

·　tf2zpk：变离散时间传递函数为零极点增益形式；

·　zp2sos：变零极点增益形式为二阶分割形式；

·　zp2ss：变零极点增益形式为状态空间形式；

·　zp2tf：变零极点增益形式为传递函数形式。

10.2.5　FIR滤波器设计（FIR Digital Filter Design）

在该工具箱里包含以下几个函数：

·　cfirpm：复杂非线性相位等纹波滤波器设计；

·　dfilt：用面向对象的方式产生滤波器；

·　fir1：基于窗函数的FIR滤波器设计；

·　fir2：基于频率取样的FIR滤波器设计；

·　fircls：多波段有限最小二乘FIR滤波器设计；

·　fircls1：低通和高通线性相位FIR滤波器的有限最小二乘设计；

·　firgauss：高斯FIR滤波器设计；

·　firls：最小二乘线性相位FIR滤波器设计；

·　firpm：Parks-McClellan最优化FIR滤波器设计；

·　firpmord：Parks-McClellan最优化FIR滤波器阶估计；

·　firrcos：升余弦FIR滤波器设计；

·　intfilt：内插FIR滤波器设计；

·　kaiserord：用Kaiser窗进行设计的FIR滤波器的参数估计；

·　sgolay：Savitzky-Golay滤波器设计。

10.2.6　IIR滤波器设计（IIR Digital Filter Design）

在该工具箱里包含以下几个函数：

·　butter：Butterworth（巴特沃思）模拟和数字滤波器设计；

·　cheby1：Chebyshev（切比雪夫）Ⅰ型滤波器设计；

·　cheby2：Chebyshev Ⅱ型滤波器设计；

·　dfilt：用面向对象的方法产生滤波器；

·　ellip：椭圆滤波器设计；

·　filtstates：包含滤波器状态信息的对象；

·　maxflat：归一化数字Butterworth滤波器设计；

·　yulewalk：递归数字滤波器设计。

10.2.7　IIR滤波器阶的选择（IIR Filter Order Estimation）

在该工具箱里包含以下几个函数：

·　buttord：计算Butterworth滤波器的阶和截止频率；

·　cheb1ord：计算Chebyshev Ⅰ型滤波器的阶；

·　cheb2ord：计算Chebyshev Ⅱ型滤波器的阶；

·　ellipord：计算椭圆滤波器的最小阶。

10.2.8　变换（Transforms）

在该工具箱里包含以下几个函数：

·　bitrevorder：将输入序列按比特反向变换；

·　czt：线性调频Z变换；

·　dct：离散余弦变换（DCT）；

·　dftmtx：离散傅立叶变换矩阵；

·　digitrevorder：将输入序列按数字反向变换；

·　fft：一维快速傅立叶变换；

·　fft2：二维快速傅立叶变换；

·　fftshift：重新编排FFT函数的输出；

·　goertzel：用二阶Goertzel算法计算离散傅立叶变换；

·　hilbert：希尔伯特变换；

·　idct：逆离散余弦变换；

·　ifft：一维逆快速傅立叶变换；

·　ifft2：二维逆快速傅立叶变。

10.2.9　统计信号处理和谱分析（Statistical Signal Processing and Spectral Analysis）

在该工具箱里包含以下几个函数：

·　corrcoef：计算相关系数矩阵；

·　corrmtx：计算自相关矩阵的数据矩阵；

·　cov：协方差矩阵；

·　cpsd：两个信号的互谱密度估计；

·　dspdata：DSP数据对象的参数信息；

·　dspopts：频谱对象的可选参数信息；

·　mscohere：两个信号之间的幅度自相关函数估计；

·　pburg：基于Burg方法的功率谱密度估计；

·　pcov：基于协方差方法的功率谱密度估计；

·　peig：基于特征向量方法的伪谱；

·　periodogram：基于周期图的功率谱密度估计；

·　pmcov：基于修正协方差方法的功率谱密度估计；

·　pmtm：基于MTM方法的功率谱密度估计；

·　pmusic：基于MUSIC算法的功率谱密度估计；

·　pwelch：基于Welch方法的功率谱密度估计；

·　pyulear：基于Yule-Walker AR方法的功率谱密度估计；

·　rooteig：基于特征向量方法的频率和功率分析；

·　rootmusic：基于root MUSIC算法的频率和功率分析；

·　spectrum：含有频谱估计方法的参数信息的对象；

·　tfestimate：从输入和输出估计传递函数；

·　xcorr：互相关函数估计；

·　xcorr2：二维互相关函数估计；

·　xcov：互协方差函数估计。

10.2.10　窗函数（Windows）

在该工具箱里包含以下几个函数：

·　barthannwin：修正的Bartlett-Hann窗；

·　bartlett：Bartlett（巴特利特）窗；

·　blackman：Blackman（布莱克曼）窗；

·　blackmanharris：最小化4阶Blackman-Harris窗；

·　bohmanwin：Bohman窗；

·　chebwin：Chebyshev窗；

·　flattopwin：平坦顶部窗；

·　gausswin：Gaussian（高斯）窗；

·　hamming：Hamming（汉明）窗；

·　hann：Hann（汉宁）窗；

·　kaiser：Kaiser（凯泽）窗；

·　nuttallwin：Nuttall定义的最小化4阶Blackman-Harris窗；

·　parzenwin：Parzen窗；

·　rectwin：矩形窗；

·　sigwin：用面向对象方法生成窗；

·　triang：三角窗；

·　tukeywin：Tukey窗；

·　window：窗函数生成；

·　wvtool：窗可视化工具。

10.2.11　参数化建模（Parametric Modeling）

在该工具箱里包含以下几个函数：

·　arburg：基于Burg方法的AR模型参数估算；

·　arcov：基于协方差方法的AR模型参数估算；

·　armcov：基于修正协方差方法的AR模型参数估算；

·　aryule：基于Yule-Walker方法的AR模型参数估算；

·　ident：查看系统识别工具箱文件；

·　invfreqs：模拟滤波器拟合频率响应；

·　invfreqz：离散滤波器拟合频率响应；

·　prony：利用Prony法的离散滤波器拟合时间响应；

·　stmcb：利用Steiglitz-McBride迭代方法求线性模型。

10.2.12　特殊操作（Specialized Operations）

在该工具箱里包含以下几个函数：

·　buffer：将信号向量缓存在数据帧矩阵中；

·　cell2sos：将二阶分区的单元序列转换为二阶分区矩阵；

·　cplxpair：将复数归成复共轭对；

·　demod：通信仿真中的解调；

·　dpss：离散椭球体序列（Slepian序列）；

·　dpssclear：清除数据库中的Slepian序列；

·　dpssdir：Slepian序列的数据库目录；

·　dpssload：从数据库中加载Slepian序列；

·　dpsssave：保存Slepian序列；

·　eqtflength：使传输函数分子和分母等长；

·　modulate：通信仿真中的调制；

·　seqperiod：计算序列周期；

·　sos2cell：将二阶分区矩阵转换为单元序列；

·　specgram：频谱分析；

·　stem：离散数据序列作图；

·　strips：条状图；

·　udecode：将2n进制整型输入解码为浮点数输出；

·　uencode：将浮点数输入编码为整型输出。

10.2.13　模拟低通滤波器原型（Analog Lowpass Filter Prototypes）

在该工具箱里包含以下几个函数：

·　besselap：Bessel模拟低通滤波器原型；

·　buttap：Butterworth模拟低通滤波器原型；

·　cheblap：Chebyshev Ⅰ型模拟低通滤波器原型；

·　cheb2ap：Chebyshev Ⅱ型模拟低通滤波器原型；

·　ellipap：椭圆模拟低通滤波器原型。

10.2.14　模拟滤波器设计（Analog Filter Design）

在该工具箱里包含以下几个函数：

·　besself：Bessel模拟滤波器设计；

·　butter：Butterworth模拟数字滤波器设计；

·　cheby1：Chebyshev Ⅰ型滤波器设计；

·　cheby2：Chebyshev Ⅱ型滤波器设计；

·　ellip：椭圆滤波器设计。

10.2.15　模拟滤波器转换（Analog Filter Transformation）

在该工具箱里包含以下几个函数：

·　lp2bp：将低通模拟滤波器转换为带通滤波器；

·　lp2bs：将低通模拟滤波器转换为带阻滤波器；

·　lp2hp：将低通模拟滤波器转换为高通滤波器；

·　lp2lp：改变模拟低通滤波器的截止频率。

10.2.16　滤波器离散化（Filter Discretization）

在该工具箱里包含以下几个函数：

·　bilinear：双线性变换法实现模拟到数字的滤波器变换；

·　impinvar：脉冲响应不变法实现模拟到数字的滤波器变换。

10.2.17　对数倒谱分析（Cepstral Analysis）

在该工具箱里包含以下几个函数：

·　cceps：倒谱分析；

·　icceps：逆倒谱分析；

·　rceps：实倒谱和最小相位重构。

10.2.18　线性预测（Linear Prediction）

在该工具箱里包含以下几个函数：

·　ac2poly：将自相关序列转换为预测多项式；

·　ac2rc：将自相关序列转换为反射系数；

·　is2rc：将反正弦参数转换为反射系数；

·　lar2rc：将对数域比例参数转换为反射系数；

·　levinson：Levinson-Durbin递归算法；

·　lpc：计算线性预测系数；

·　lsf2poly：将线性谱频率转换为预测系数；

·　poly2ac：将预测多项式转换为自相关序列；

·　poly2lsf：将预测系数转换为线性谱频率；

·　poly2rc：将预测多项式转换为反射系数；

·　rc2ac：将反射系数转换为自相关序列；

·　rc2is：将反射系数转换为反正弦参数；

·　rc2lar：将反射系数转换为对数域比例参数；

·　rc2poly：将反射系数转换为预测多项式；

·　rlevinson：逆Levinson-Durbin递归；

·　schurrc：利用自相关序列计算反射系数。

10.2.19　多速信号处理（Multirate Signal Processing）

在该工具箱里包含以下几个函数：

·　decimate：降低序列的采样速率；

·　downsample：采样速率整数倍下降；

·　interp：提高采样速率；

·　interp1：一维数据插值；

·　resample：按有理数因数改变采样率；

·　spline：三次样条函数内插；

·　upfirdn：过采样，FIR滤波，取样；

·　upsample：采样速率整数倍提高。

10.2.20　图形用户接口（Graphical User Interfaces）

在该工具箱里包含以下几个函数：

·　fdatool：打开滤波器设计和分析工具；

·　fvtool：打开滤波器可视化工具；

·　sptool：交互式数字信号处理工具（SP工具）；

·　wintool：打开窗函数设计和分析工具；

·　wvtool：打开可视窗工具。

10.3　基于MATLAB的信号处理系统分析与设计

本节主要介绍MATLAB在信号处理领域一些常用的实例，是对前两节基础知识的综合运用。

10.3.1　离散信号与系统的MATLAB实现

【例10.1】离散信号的运算是实现各种信号和系统的基础，本例给出信号基本运算的MATLAB实现，包括位移、相加、相乘以及变换等。

给定离散信号为x₁(n)和x₂(n)，信号y₁(n)＝x₁(n－k)，y₂(n)＝x₁(n＋k)，x(n)＝x₁(n)＋x₂(n)，y(n)＝x₁(n)x₂(n)，编写程序实现上述运算，并且计算x(n)的功率和能量，对x(n)进行信号折叠和奇偶分解。

MATLAB程序代码如下：

【例10.2】用MATLAB编写生成均值为a，方差为b的高斯随机序列信号。

MATLAB程序代码如下：

以上是离散信号的产生例子，在实际操作中可以灵活运用MATLAB提供的各种运算和工具箱函数实现系统需要的信号形式。

分析一个离散系统最重要的是得到其系统单位抽样响应，用filter函数或者impz函数即可实现。

【例10.3】求如图10-9所示的离散系统的单位抽样响应。

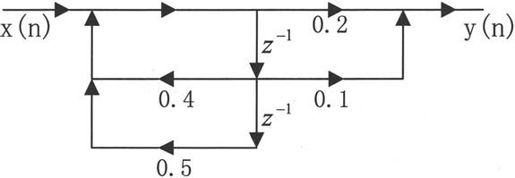
图10-9　离散系统的信号流图

该离散系统对应的输入输出差分方程为：

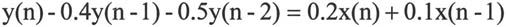
MATLAB程序代码如下：

程序采用MATLAB给出的两种函数filter和impz来计算，得到的系统单位响应曲线如图10-10所示，从图中可以看出两函数求得的结果相同。

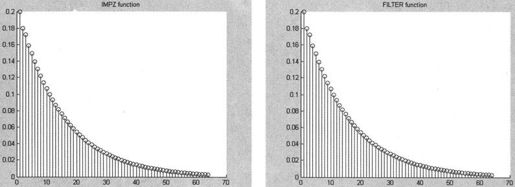
图10-10　单位抽样响应

在进行离散系统的分析时，系统的频率响应和零极点增益也是常常需要考虑的问题，可分别用freqz函数和roots函数来实现。

10.3.2　离散傅立叶变换的MATLAB实现

周期序列实际上只有有限个序列值有意义，因此它的许多特性可以沿用到有限长序列上，由离散傅立叶级数的公式可以得到有限长序列的离散傅立叶变换的公式，在第1节中有具体的介绍。如果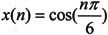是一个N为12的序列，利用MATLAB计算其DFT并画出图形。

【例10.4】在MATLAB中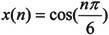（N为12）DFT的实现。

MATLAB程序代码如下：

运行后得到的结果如下：

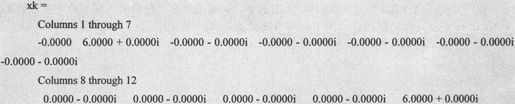
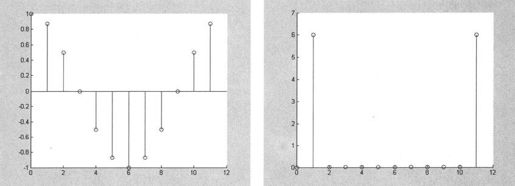
图10-11　有限序列和序列的DFT

同样由IDFT公式也可以编写相应的程序：

在进行快速傅立叶变换FFT的操作时可以调用内部函数fft，速度比较快。DFT和FFT在信号处理中有着重要的应用，可以进行卷积运算，实现线性时不变系统等。

【例10.5】设x(n)长度为N₁，h(n)长度为N₂，计算两者的线性卷积，其步骤如下：

·　将x(n)和h(n)通过增加零值延长到N＝N₁＋N₂－1；

·　利用FFT计算x(n)和h(n)各自N点的DFT；

·　计算Y(k)＝X(k)H(k)；

·　利用IFFT计算Y(k)便可得到卷积结果y(n)。

对于特定的序列，MATLAB程序代码如下：

运行结果如图10-12所示。

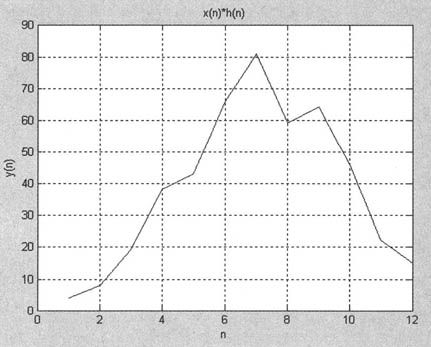
图10-12　应用FFT计算线性卷积

10.3.3　Z变换的MATLAB实现

有关Z变换的定义和性质在10.1节中已有介绍，对于Z变换为X(z)的序列，MATLAB的表示是通过X(z)的系数实现的，Z变换经常用到deconv、residuez和freqz等函数。

【例10.6】计算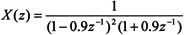|z|＞0.9的逆Z变换。

其MATLAB程序代码如下：

执行完毕的结果代码为：

因此得到下面的表达式：

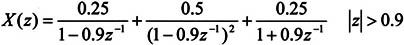
相应的逆Z变换为下面的表达式：

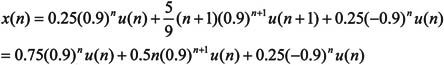
【例10.7】用MATLAB实现由系统的差分方程求出系统的冲激响应，画出其幅度相位响应，并指出系统的零、极点，差分方程为：

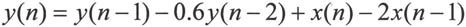
MATLAB程序代码如下：

可得系统的零极点为：

系统的冲激响应、幅度响应和相位响应如图10-13所示。

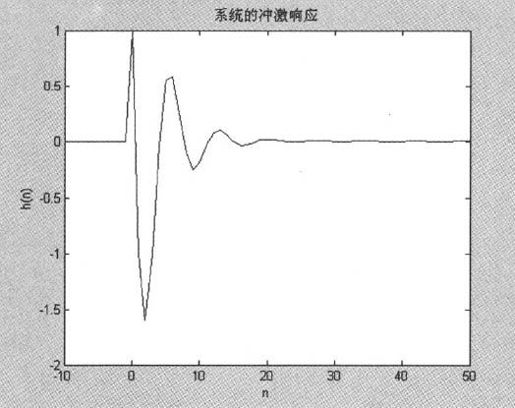
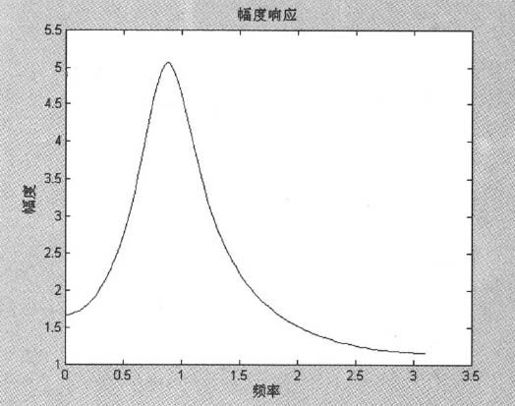
图10-13　系统的冲激响应、幅度响应和相位响应

此外，Z变换还可用于差分方程的求解。

10.3.4　FIR滤波器的MATLAB实现

基于MATLAB的FIR滤波器的设计有多种方法，包括窗函数法（对应的MATLAB函数有fir1、fir2、kaiserord）、最优化设计法（对应的MATLAB函数有firls、remez、remezord）、最小二乘约束设计法（fircls、fircls1）、非线性相位滤波器设计法（cremez）和升余弦方法（firrcos）本节将举例说明fir1、fir2、kaiserord和firls、remez如何用于滤波器的设计。

【例10.8】设计一个阶数为48，通带范围为0.35≤w≤0.65的带通FIR线性相位滤波器，并分析它的频率特性。

MATLAB程序代码如下：

得到的频率特性如图10-14所示。

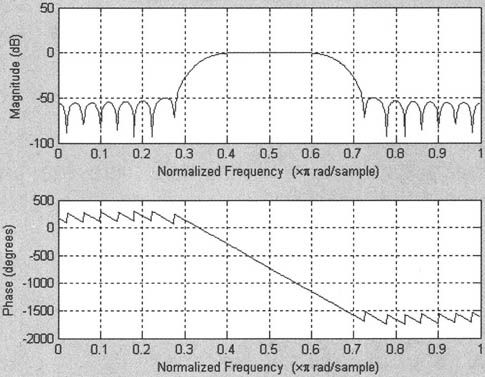
图10-14　利用fir1设计的带通滤波器的频率响应

【例10.9】设计一个60阶的滤波器，要求设计的滤波器0～π／8的幅度为1，在π／8～2π／8的幅度为1／2，在2π／8～4π／8的幅度响应为1／4，在4π／8～6π／8的幅度响应为1／6，在6π／8～π的响应为1／8，并且画出理想滤波器和设计得到的滤波器的幅度频率响应进行比较。

MATLAB程序代码如下：

得到的频率响应如图10-15所示。

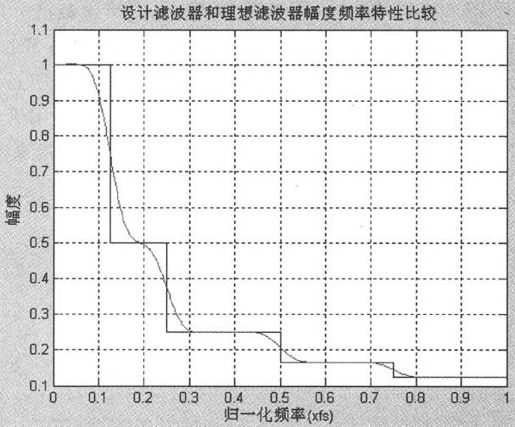
图10-15　利用fir2设计的任意频率响应的滤波器

【例10.10】利用凯塞窗函数设计一个长度为奇数的带通滤波器（长度为奇数对应滤波器是偶阶的，由此能满足带通滤波器的要求），通带范围是1300Hz～2210Hz，阻带范围是0Hz～1000Hz、2410Hz～4000Hz，阻带的波纹最大为0.01，通带的波纹最大为0.05，信号的采样频率为8000Hz。

MATLAB程序代码如下：

得到的滤波器的阶数为90，滤波器的截止频率分别为0.2875和0.5775，凯塞窗函数的β值为3.3953。滤波器的频率响应如图10-16所示。

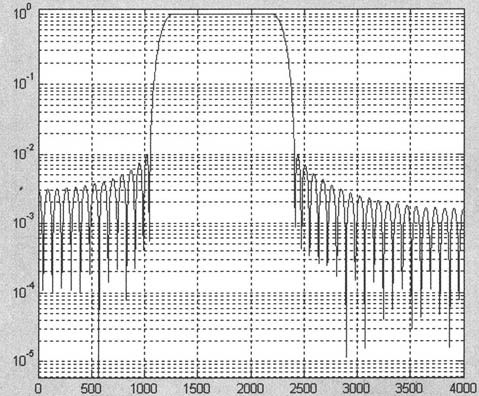
图10-16　利用kaiserord设计的滤波器的频率响应

【例10.11】分别用函数firls和remez设计一个30阶的FIR低通滤波器，通带边界频率为0.4π，幅值为3，阻带边界频率为0.5π，幅值为1，并比较两函数设计的FIR滤波器。

注意：函数firls是fir1和fir2的扩展，其基本设计准则是利用最小二乘法使期望的频率响应和实际的频率响应之间的整体误差最小。函数remez实现Parks-Mcclellan算法，它利用Remez交换法和Chebyshev近似理论来设计滤波器，使实际频率响应拟合频率响应达到最优。

MATLAB程序代码如下：

程序运行结果如图10-17所示。

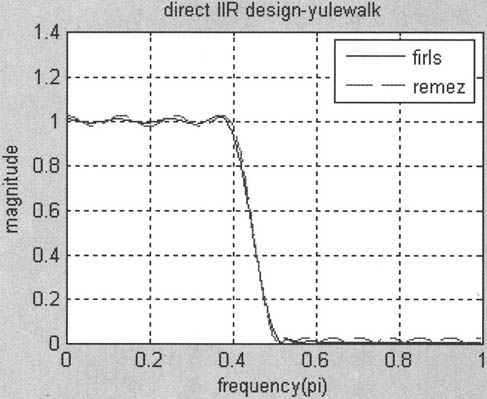
图10-17　FIR滤波器频率响应

可见用firls设计的滤波器在整个频率范围内均具有良好的频率响应，但理想频率响应和实际频率响应的误差在带区内不均匀，且在边界频率处误差较大，而用函数remez设计的滤波器在通带内有等波纹特性，在边界频率0.4π和0.5π处及过渡带内更接近于理想频响。

10.3.5　IIR滤波器的MATLAB实现

IIR滤波器的设计主要有模拟滤波器变换法（经典设计法）、直接设计法和最大平滑滤波器设计法三种方法。本节将列举具有代表性的例程来说明三种方法的应用。

·　经典设计法是基于模拟滤波器的变换原理，首先根据滤波器的技术指标设计出相应的模拟滤波器，然后再离散化为满足给定技术指标的数字滤波器。在MATLAB中对应的工具函数有完全设计函数——butter、cheby1、cheby2、ellip、besself；阶数估计函数——buttord、cheblord、cheb2ord、ellipord；低通模拟原型滤波器函数——buttap、cheb1ap、cheb2ap、ellipap；频率转换函数——lp2lp、lp2bp、lp2hp、lp2bs；滤波器离散化函数——bilinear、impinvar。

·　直接设计法是在离散域内用最小二乘法逼近给定的幅频特性，在MATLAB中对应的工具函数是yulewalk。

·　最大平滑滤波器设计法是设计一般化低通滤波器，其零点数多于极点，在MATLAB中对应的工具函数是maxflat。

【例10.12】经典法设计滤波器的设计有脉冲响应不变法和双线性变换法两种方式。

·　用椭圆滤波器原型设计一个低通滤波器，满足ω_p＝0.2π、R_p＝0.5dB、ω_s＝0.3π、A_s＝20dB，采用脉冲响应不变法。

MATLAB程序代码如下：

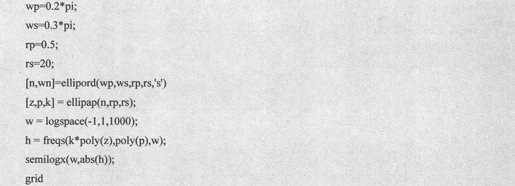
运行结果如图10-18所示。

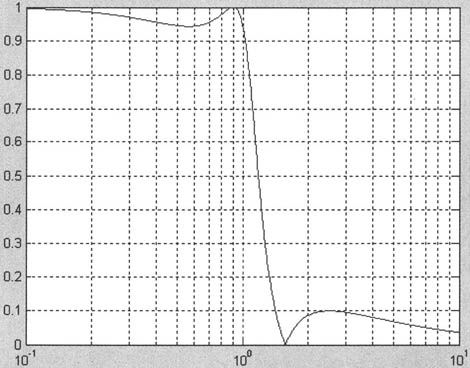
图10-18　椭圆低通滤波器的频响特性

·　采用双线性变换法设计带通ChebyshevⅠ型数字滤波器，要求通带边界频率为100～200Hz；通带纹波小于3dB；阻带衰减大于30dB；过渡带宽为30Hz；采样频率为1000Hz。

MATLAB程序代码如下：

程序运行结果如图10-19所示。

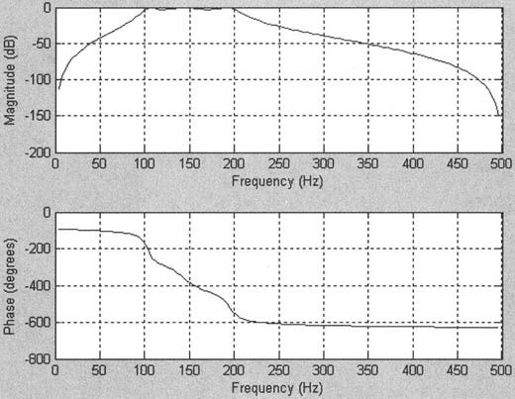
图10-19　ChebyshevⅠ型数字滤波器的频率特性图

【例10.13】用直接法设计一个多频带数字滤波器，幅频响应值如下：

f＝[00.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1]；

M＝[0 0 1 1 0 0 1 1 0 0 0]；

采用函数yulewalk来实现，具体操作步骤如下：

·　计算与分子多项式相应的幅值平方响应的辅助分子式和分母式；

·　由辅助分子式和分母式计算完全的频率响应；

·　计算滤波器的脉冲响应；

·　采用最小二乘法拟合脉冲响应，最终求得滤波器的分子多项式。

MATLAB程序代码如下：

程序运行结果如图10-20所示。

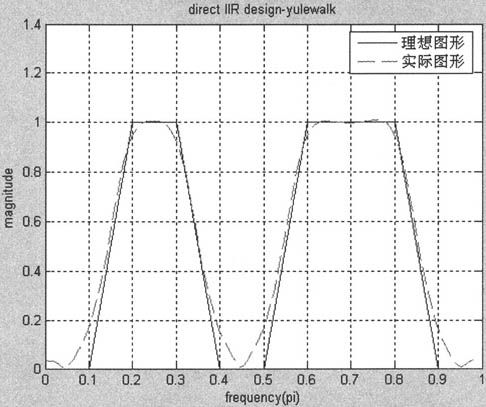
图10-20　直接设计的多频带滤波器

【例10.14】用maxflat函数设计一个通用Butter-Worth低通滤波器，满足系统函数分子阶数为8阶，系统函数分母阶数为3阶，截止频率为1*π。

MATLAB程序代码如下：

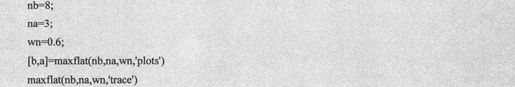
程序运行结果如下：

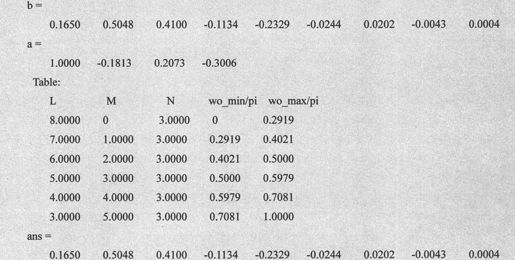
由上述代码得到如图10-21所示的图形。

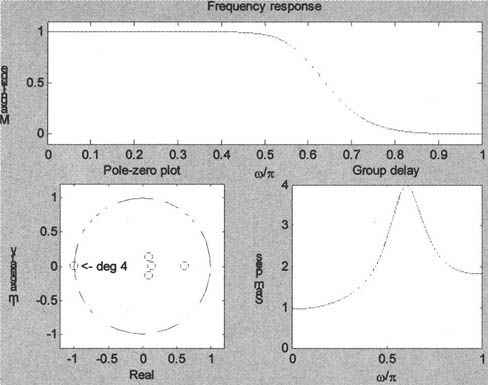
图10-21　最大平滑Butter-Worth低通滤波器特性