第3章　视频压缩编码的基本原理

3.1　预测编码

3.1.1　预测编码的基本概念

预测法是最简单、实用的视频压缩编码方法，经过压缩编码后传输的并不是像素本身的取样值，而是该取样的预测值和实际值之差。

为什么取像素预测值与实际值之差作为传输的信号？因为大量统计表明，同一幅图像的邻近像素之间有着相关性，或者说这些像素值相似，如图3.1所示。邻近像素之间发生突变或“很不相似”的概率很小。而且同帧图像中邻近行之间对应位置的像素之间也有较强的相关性。人们可以利用这些性质进行视频压缩编码。

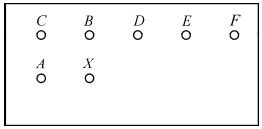
图3.1　邻近像素间的相关性

以同一帧内邻近像素为例，当前像素为X，其左邻近像素为A，上邻近像素为B，上左邻近像素为C等。显然，与X之间的距离近的像素，如A和B，与X的相关性强；与X之间的距离远的像素，如C、D、E、F，与X的相关性弱。以P作为预测值，按与X的距离不同给以不同的权值，把这些像素的加权和作为X的预测值，与实际值相减，得到差值q。由于临近像素之间相关性强，q值非常小，可以达到压缩编码的目的。

接收端把差值q与预测值（事先已定义好，比当前X早到达接收端的像素，如A）相加，恢复原始值X。归纳如下：

编码端：X－A＝q

解码端：q＋A＝X

按以上原理可得预测编码框图，如图3.2所示。这种预测编码也称为差分脉冲编码（DPCM）。

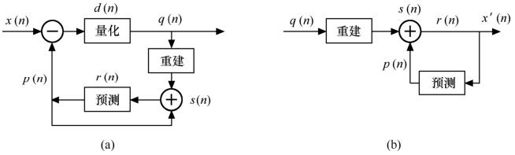
图3.2　预测编码

其中，x(n)为当前像素的实际值，p(n)为其预测值，d(n)为差值或残差值。该差值经量化后得到残差量化值q(n)。预测值p(n)经预测器得到，预测器输入为已存储在预测器内前面的各像素及其当前值，它们的加权和即为下一个预测器输出。

由图3.2可见，解码输出x′(n)与原始信号x(n)之间有个因量化而产生的量化误差。

现在进一步说明预测法可压缩视频信息的理由。大量统计表明，由于相关性的存在，邻近像素值之差很小。其差值信号的概率分布如图3.3所示。可见，该差值信号的方差是比较小的。由于图像的误差信号d(n)的方差比图像信号本身的方差小，其量化器的动态范围可以缩小，相应的量化分层数目就可减少，每个像素的编码比特数也显著下降，而且不会使视频质量明显降低，达到视频压缩的目的。

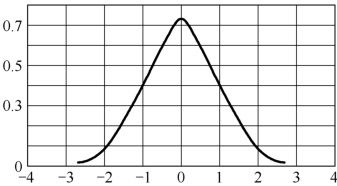
图3.3　图像差值信号的概率分布

3.1.2　帧内预测编码

1．一维最佳预测

现在按上述的概念重新画成图3.4所示的预测编码器。

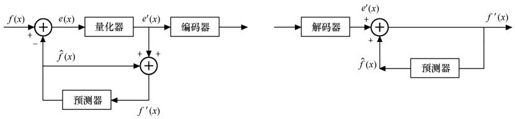
图3.4　一维预测编码器

预测模型可以是一维的，也可以是二维或多维的；可以是线性的，也可是非线性的。下面先讨论一维线性预测方法。

设预测值为：

其中，f(x)为当前像素值，以f(x)为基准，f(x－1)为前一个像素值，f(x－2)为前面第二个像素值。把前m个像素值的加权和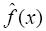作为f(x)的预测值。a_k是预测系数，m为预测阶数。其预测误差如下：

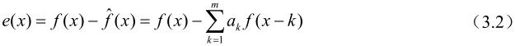
e(x)经量化得到e′(x)，为获得最佳预测效果，应使e(x)的均方误差最小，此时编码效率最高：

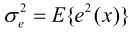
令

设E{f(x－j)f(x－k)}＝R_k-j为信号间的相关函数，因信号是平稳信源，即像素间自相关是常数，与位置无关，像素间相关性对称，可得出：

即预测系数：

可以证明，这时预测误差的方差为：

可见，相关性R_k越大，预测误差方差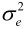越小于信号方差，压缩效率也就越高。

2．二维最佳预测

二维预测编码器框图如图3.5所示。

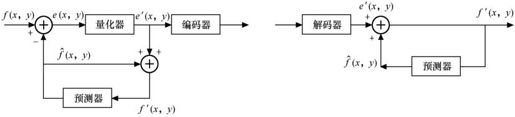
图3.5　二维预测编码

图3.5中f(x, y)为当前像素值，(x, y)为其所在水平和垂直位置的坐标值。由一维预测可推广，其二维预测值为：

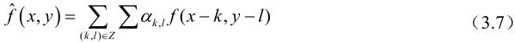
其中，α_k,l为二维预测系数，Z为预测区域，（k,l）分别为对当前点进行预测的像素的水平和垂直位置坐标值。设f(x, y)为二维平稳随机过程，预测误差为：

令

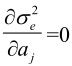
得：

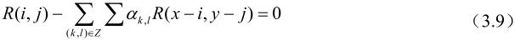
由二维图像得相关函数，可得其预测误差方差为：

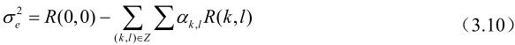
为了利用数字电路实现预测系数，往往将其取为1/2、1/4、1/8之类的分数。有人提出了以下预测值：

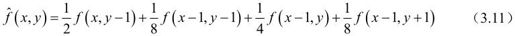
其中，各预测点的位置如图3.6所示。

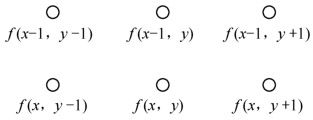
图3.6　二维图像像素位置

3．预测编码增益

视频预测编码的效果是得到了视频的压缩编码，即相对于不压缩的PCM而言，每个像素值被分配的比特数被减少。换言之，可用相同比特率下产生的量化失真之比来定义编码增益。

由本章参考文献［3］可知，对于PCM，其率失真D_PCM为：

其中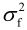，为原始信号的方差，ε为量化误差的概率密度函数。如预测误差采用最佳标量量化，量化失真D_DPCM与码率R之间关系为：

其中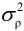，为预测误差的方差，是预测误差的概率密度函数，预测编码增益为：

对于高斯信源，ε²和两者可以认为相等，于是得：

例：对一幅图像中每个2×2块进行预测编码（如图3.7所示），其中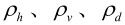分别为相邻像素之间的相关系数，设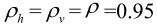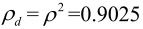，，求G_DPCM。

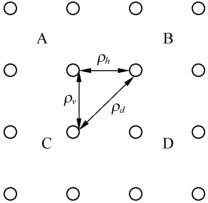
图3.7　2×2块

解：由式（3.4）、式（3.5）和式（3.6）的推导可知：

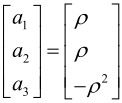
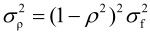
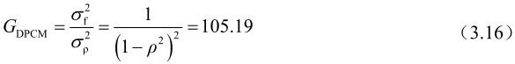
4．预测编码的量化器

图3.3中给出了大量统计后差值信号的概率分布，一般说来，图像中平坦区域比突变区域多得多，例如人脸中只有眼睛、鼻子、嘴等少量地方有细节出现，其余则为平坦或缓变区域。

人眼视觉特性的实验表明，在亮度突变部分或变化大的部分，量化误差大些不会使人眼敏感，可采取粗量化，量化节距可取大一些，这时虽然需要较多的比特数，但面积小，总比特数不大；反之，在亮度变化缓慢区域，则应取细量化，但由于平坦区域e(x, y)小，也不会增加很多比特数。总之，依据视觉掩蔽效应，采用非线性（不均匀）量化，可使总码率有所下降。表3.1为量化器输入输出值举例。由于误差信号值有正有负，总量化级数为19。

表3.1　　　　量化值举例

由于量化，预测编码会产生过载、颗粒噪声、伪轮廓以及边沿忙乱等，如图3.8所示。它们都是由于量化值过小或像素变化过快等量化值跟不上变化造成的。

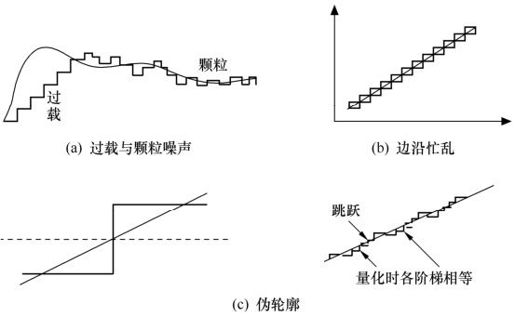
图3.8　预测编码的各种噪声

5．二维预测编码器

图3.9、图3.10为一具体的二维预测编码器、解码器举例，设原数字序列为f(x, y)，预测公式为：

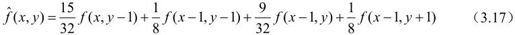
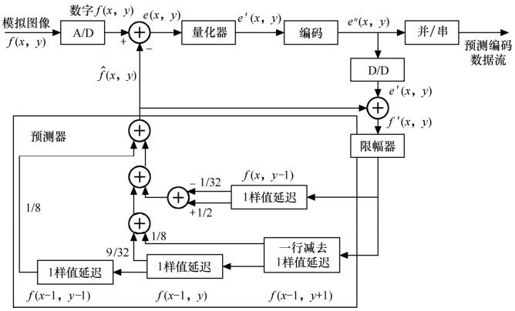
图3.9　二维预测编码器

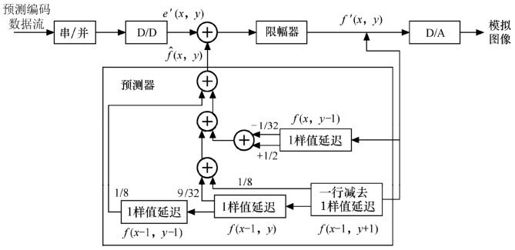
图3.10　二维预测解码器

3.1.3　帧间预测编码

一般而言，帧间预测编码的编码效率比帧内编码更高。有人测得，对缓慢变化256级灰度的黑白图像序列，帧间差超过阈值3的像素不到一帧像素的4％；对剧烈变化256亮度值的彩色电视序列，帧间差超过阈值6的像素平均只占一帧的7.5％。下文将讨论单向预测、双向预测、重叠块运动补偿三部分内容。

1．单向预测

（1）预测原理

图3.11所示为单向预测的预测编码框图。

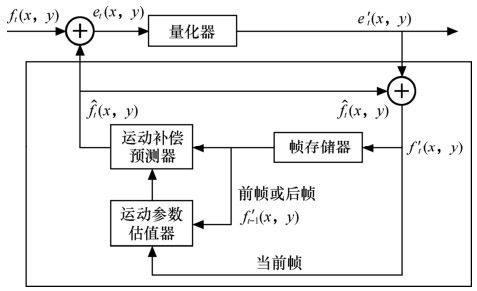
图3.11　单向预测帧间编码

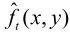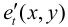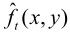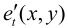当前帧图像f_t(x , y)与预测图像相减后的帧误差e_t(x , y)，经量化器量化后输出，传送到信道。预测图像与相加，得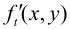，当不计量化失真时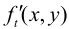，即当前的f_t(x , y)。

把当前帧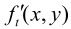与帧存储器输出的前一帧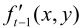（也称参考帧）同时输入到运动参数估值器中，经搜索、比较得到运动矢量MV。此MV输入到运动补偿预测器中，得到预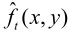测图像。预测图像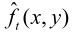不可能完全等同于当前图像f_t(x, y)，无论预测得如何精确，总存在帧误差e_t(x , y)。

由上述可知，利用上一帧的图像经运动矢量位移作为预测值的方法称为单向预测或单向时间预测。这时，有

其中，（i, j）即运动矢量。

如何减小帧差和更精确地预测当前像素，是提高帧间压缩编码效率的关键。

（2）基于块匹配算法的运动矢量估计

上述原理以像素为单位进行预测，除了传送帧差外，还增加了每个像素的运动矢量，编码效率明显下降。

实际上，两帧之间的物体运动一般是刚体的平移运动，位移量不大，因此往往把一帧图像分成若干M×N块，以块为单位分配运动矢量，大大降低了总码率。如图3.12所示。

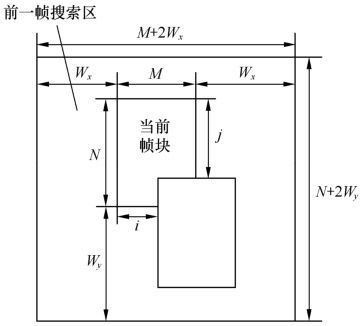
图3.12　块匹配算法

设前一帧搜索区为（M＋2W_x，N＋2W_y），当前帧块与前一帧块的位移为d(i, j)，在搜索区中，如能找到与当前帧块匹配的前一帧块，则该d(i, j)即为所需的运动矢量。

常用的匹配准则有：

①均方误差（MSE）最小准则：

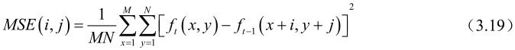
②绝对误差均值（MAD）最小准则：

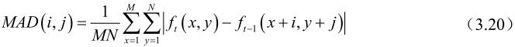
（3）搜索方法

①穷尽搜索法。穷尽搜索法是对搜索窗内的每一点都用匹配准则进行计算，找到MSE或MAD最小时的点(i, j)值，作为所需的运动矢量d(i, j)。

该法计算量大，如采用MAD准则，需计算（2W_x＋1）×（2W_y＋1）个MAD值，但它能够找到全局最优运动矢量。

②快速搜索法。为了更快地找到d(i, j)，可采用一些快速搜索法，这里只以三步搜索法为例加以说明，如图3.13所示。

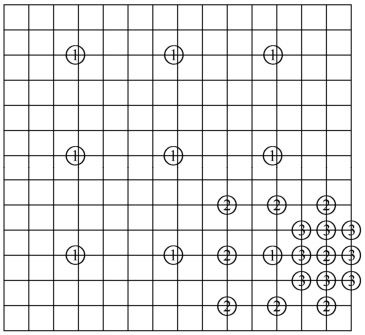
图3.13　三步搜索法

一个16×16搜索区中心点为(i, j)＝(0,0)，以搜索区最大搜索长度的一半为步长，计算中心点及其周围8个邻近点的MAD值，如找到某个点MAD值最小，再以该点为中心，步长减为原来的一半，依次类推。到了第三步，再把步长减半，计算MAD值，其中MAD值最小点的运动矢量即为所求的值。快速算法的速度快，但不能保证全局最优。

2．双向预测

有时，不只是利用前一帧像素进行预测，还需利用后一帧像素，即预测值为：

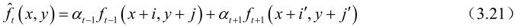
其中，d(i, j)和d(i′, j′)分别为t到t－1和t到t＋1间的运动矢量MV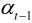，和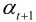分别为前向和后向预测系数，可按最佳预测公式确定。

这时，用前向参考帧预测当前帧称为前向运动补偿，利用后向参考帧预测当前帧称为后向运动补偿，利用前、后向同时预测，就称为双向预测运动补偿。

在诸如会议电视、可视电话等实时通信中，一般不应用双向预测，因为后向预测在当前帧之后进行，会引入编码时延。它可用在广播电视系统中，如采用MPEG标准的编码系统，特别针对一些暴露区域，即t－1帧尚未暴露而t＋1帧已呈现出来的区域。图3.14为单向和双向预测编码举例。

为了进一步提高编码效率，多帧预测（包括单向和双向预测）被引入，如H.264标准参考帧可达16帧。

3．重叠块运动补偿OBMC

以上基于块的运动补偿从计算量上看是比较简单，但这种人为的块划分使得每个块有一个运动矢量，容易产生方块效应，特别在运动矢量估计不准确或物体运动非简单的平移运动及一个块中有几个不同运动物体时更为严重。重叠块运动补偿（OBMC，Overlapped Block Motion Compensation）方法解决了运动矢量估计不准确的问题。

采用OBMC方法时，一个像素的预测不仅基于它所属的MV估计，还基于其相邻的MV估计。如图3.15所示，以4个邻块为例。

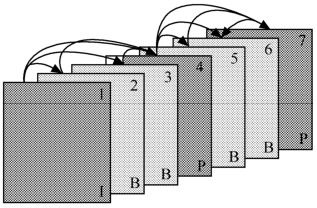
图3.14　单向和双向预测举例

图3.15　4邻块的OBMC

这时预测值为：

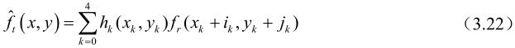
为找到最佳预测估计，应使下式最小：

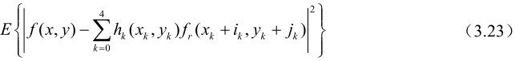
为保持图像的均值，还需加上如下约束：

3.1.4　运动估计

1．基本概念

在帧间预测编码中，由于活动图像邻近帧中的景物存在着一定的相关性，因此可将活动图像分成若干块或宏块，并设法搜索出每个块或宏块在邻近帧中的位置，并得出两者之间的空间位置的相对偏移量，得到的相对偏移量就是通常所指的运动矢量，得到运动矢量的过程被称为运动估计。

运动矢量和经过运动匹配后得到的预测误差共同发送到解码端，在解码端按照运动矢量指明的位置，从已经解码的邻近参考帧图像中找到相应的块或宏块，和预测误差相加后就得到了解码的块或宏块在当前帧中的位置。

通过运动估计可以去除帧间冗余度，使得视频传输的比特数大为减少，因此，运动估计是视频压缩处理系统中的一个重要组成部分。本小节先从运动估计的一般方法入手，重点讨论了运动估计的3个关键问题：将运动场参数化、最优化匹配函数定义以及如何寻找到最优化匹配。

2．运动估计的方法

一般的运动估计方法如下：设t时刻的帧图像为当前帧f(x, y)，t′时刻的帧图像为参考帧f′(x, y)，参考帧在时间上可以超前或者滞后于当前帧。如图3.16所示，当t′<t时，称之为前向运动估计，当t′>t时，称之为后向运动估计。当在参考帧t′中搜索到当前帧t中的块的最佳匹配时，可以得到相应的运动场d(x; t, t ±△t)，即可得到当前帧的运动矢量。

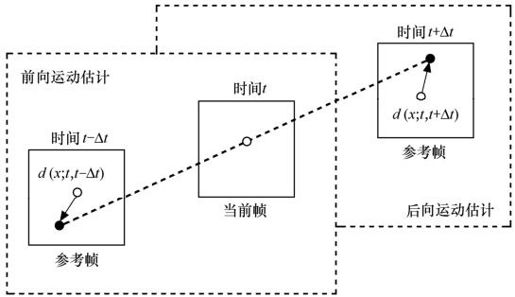
图3.16　前向和后向运动估计

H.264编码标准和以往采用的视频压缩标准的最大不同在于，在运动估计过程中采用了多参考帧预测来提高预测精度。多参考帧预测就是在编解码端建一个存储M个重建帧的缓存，当前的待编码块可以在缓存内的所有重建帧中寻找最优的匹配块进行运动补偿，以便更好地去除时间域的冗余度。由于视频序列的连续性，当前块在不同的参考帧中的运动矢量也是有一定的相关性的。假定当前块所在帧的时间为t，则对应前面的多个参考帧的时间分别为：t－1，t－2，…则当在帧t－2中搜索当前块的最优匹配块时，可以利用当前块在帧t－1中的运动矢量MV_NR来估测出当前块在帧t－2的运动矢量。

3．运动表示法

由于在成像的场景中一般有多个物体做不同的运动，如果直接按照不同类型的运动将图像分割成复杂的区域是比较困难的。最直接和不受约束的方法是对每个像素都指定运动矢量，这就是基于像素表示法。这种表示法是对任何类型图像都是适用的，但是它需要估计大量的未知量，并且它的解时常在物理上不正确，除非在估计过程中施加适当的物理约束。这在具体实现时是不可能的，通常采用基于块的物体运动表示法。

（1）基于块的运动表示法

一般对于包含多个运动物体的景物，实际中普遍采用的方法是把一个图像帧分成多个块，使得在每个区域中的运动可以很好地用一个参数化模型表征，这被称为块匹配法。即将图像分成若干个n×n块（典型值：16×16宏块），为每一个块寻找一个运动矢量MV，并进行运动补偿预测编码。

每一个帧间宏块或块都是根据先前已编码的数据预测出的，根据已编码的宏块、块预测的值和当前宏块、块作差值，再把结果压缩传送给解码器，与解码器所需要的其他信息（如运动矢量、预测模型等）一起用来重复预测过程。

每个分割区域都有其对应的运动矢量，必须对运动矢量以及块的选择方式进行编码和传输。如果选择较大的块尺寸，意味着用于表明运动矢量和分割区域类型的比特数会少些，但是运动压缩的冗余度要多一些；如果选择小一点的块尺寸，运动压缩后冗余度要少一些，但是所需比特数要比较多。因此必须要权衡块尺寸选择上对压缩效果的影响，一般对于细节比较少、比较平坦的区域选择的块的尺寸大一些，对于图像中细节比较多的区域选择的块的尺寸小一些。

当采用4∶2∶0取样格式时，宏块中的每个色度块（C_b、C_r）尺寸宽、高都是亮度块的一半，色度块的分割方法和亮度块相同，只是尺寸上宽、高都是亮度块一半（如亮度块是8×16块尺寸大小，那么色度块就是4×8；如果亮度块尺寸为8×4，那么色度块便是4×2等）。每个色度块的运动矢量的水平和垂直坐标都是亮度块的一半。

（2）亚像素位置的内插

帧间编码宏块中的每个块或亚宏块分割区域都是根据参考帧中的同尺寸区域预测得到的，它们之间的关系用运动矢量来表示。

由于自然物体运动的连续性，相邻两帧之间的块的运动矢量不是以整像素为基本单位的，可能真正的运动位移量是以1/4像素甚至1/8像素等亚像素作为单位的。

一个视频序列当采用1/2像素精度、1/4像素精度和1/8像素精度时编码效率的情况如图3.17所示。可以看出，1/4像素精度相对于1/2像素精度的编码效率有很明显的提高，但是1/8像素精度相对于1/4像素精度的编码效率除了在高码率情况下并没有明显的提高，而且1/8像素的内插公式更为复杂。因此，在H.264的制定过程中，1/8像素精度的运动矢量模型逐渐被取消，而只采用了1/4像素精度的运动矢量模型。

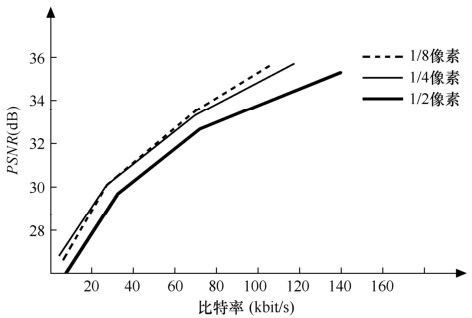
图3.17　高精度的亚像素运动搜索对编码效率的影响

（3）运动矢量在时空域的预测方式

如果对每个块的运动矢量进行编码，那么将花费相当数目的比特数，特别是选择小尺寸的块的时候。由于一个运动物体会覆盖多个分块，所以空间域相邻块的运动矢量具有很强的相关性，因此，每个运动矢量可以根据邻近先前已编码的块进行预测，预测得到的运动矢量用MV_p表示，当前矢量和预测矢量之间的差值用MV_D表示。同时由于物体运动的连续性，运动矢量在时间域也存在一定的相关性，因此也可以用邻近参考帧的运动矢量来进行预测。

①运动矢量空间域预测方式。

（a）运动矢量中值预测（Median Prediction）。利用与当前块E相邻的左边块A，上边块B和右上方的块C的运动矢量，取其中值作为当前块的预测运动矢量。

设E为当前宏块、宏块分割或者亚宏块分割，A在E的左侧，B在E的上方，C在E的右上方，如果E的左侧多于一个块，那么选择最上方的块作为A，在E的上方选择最左侧的块作为B。图3.18表示所有的块尺寸相同，图3.19表示邻近块尺寸不同时作为预测E的运动矢量的块的选择方法。

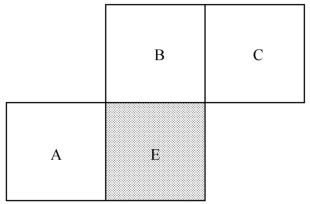
图3.18　块尺寸相同的当前块和邻近块

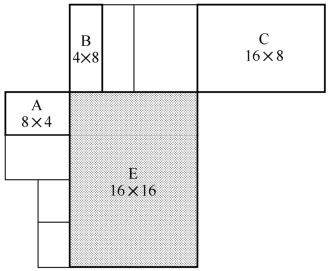
图3.19　块尺寸不同的当前块和邻近块

在预测E的过程中遵守以下准则：

（i）对于除了块尺寸为16×8和8×16的块来说，MV_p是块A、B和C的运动矢量的中值；

（ii）对于16×8块来说，上方的16×8块的MV_p根据B预测得到，下方的16×8块的MV_p根据A得到；

（iii）对于8×16块来说，左侧的16×8块的MV_p根据A预测得到，右侧的16×8块的MV_p根据C得到；

（iv）对于不用编码的可跳过去的宏块，16×16矢量MV_p可用（i）中的情况得到。

（b）空间域的上层块模式运动矢量（Uplayer Prediction）。H.264标准中提供的块尺寸有16×16、8×16、16×8、8×8、8×4、4×8、4×4，它们的图像分割区域分别定义为搜索模式Mode1～Mode7。假设当前分割区域的预测模式为Mode_curr，上层模式Mode_up定义为：

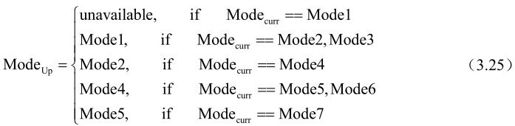
图3.20所示为利用空间域上层搜索模式的运动矢量作为当前块的预测运动矢量的预测方式。

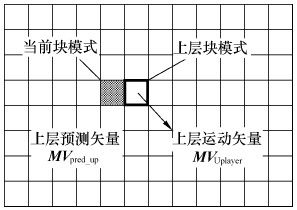
图3.20　空间域上层预测的模式

②运动矢量在时间域预测方式。

（a）前帧对应块运动矢量预测（Corresponding-block Prediction）。利用前一帧与当前帧相同坐标位置的块的运动矢量来作为当前块的预测运动矢量，如图3.21所示。

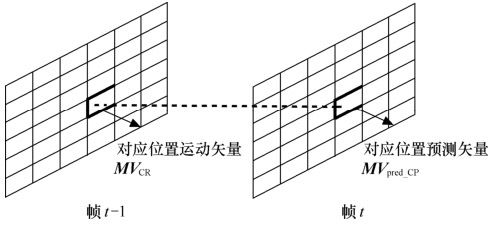
图3.21　前帧对应位置的运动矢量预测的模式

（b）时间域的邻近参考帧运动矢量预测（Neighboring Reference-frame Prediction）。由于视频序列的连续性，当前块在不同的参考帧中的运动矢量也是有一定的的相关性的。如图3.22所示，假设当前块所在帧的时间为t，则当在前面的参考帧t′中搜索当前块的最优匹配块时，可以利用当前块在参考帧t′＋1中的运动矢量来估测出当前块在帧t′中的运动矢量：

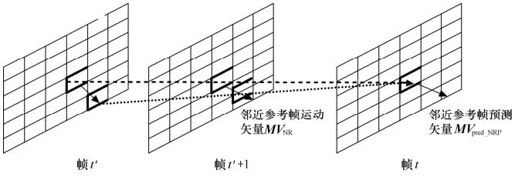
图3.22　时间域邻近参考帧预测的模式

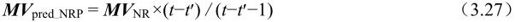
在上述运动矢量的4种预测方式中，经过实验证明，空间域的预测更为准确，其中上层块预测的性能最优，这是因为其充分利用了不同预测块模式运动矢量之间的相关性。而中值预测性能随着预测块尺寸的减小而增加，这是因为当前块尺寸越小，相关性越强。

（4）匹配误差在时空域的预测方式

H.264中定义的匹配误差函数如下：

其中SAD（绝对差值和）计算公式如下：

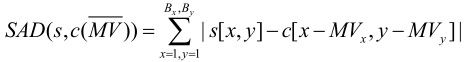
其中，s是当前进行编码的原始数据，而c是已经编码重建的用于进行运动补偿的参考帧的数据。MV为候选的运动矢量，λ_MOTION为拉格朗日常数，PMV为中值预测矢量，R(MV-PMV)代表了运动矢量差分编码可能耗费的比特数。由于在接下来的4种匹配误差预测方式中，λ_MOTION×R(MV－PMV)部分通常由于MV与PMV很接近而抵消，SAD部分的预测特性基本上可以反映整个匹配函数的预测特性，因此J（MV，λ_MOTION）可用SAD来表示。

匹配误差在时空域的预测方式和运动矢量类似，具体分为：

①匹配误差在空间域的预测方式。

（a）中值预测（Median Prediction）。与当前块E相邻的左边块A、上边块B和右上方的块C搜索得到的最小SAD值分别为SAD_A、SAD_B、SAD_C，取当前块的预测SAD值为：

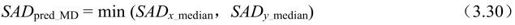
SAD_{x_median}是对应运动矢量横坐标为

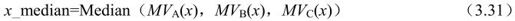
的相邻块的最小SAD值，SAD_{y_median}也同理。如图3.23所示。

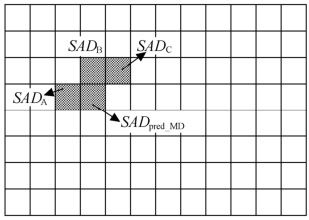
图3.23　SAD空间域中值预测模式

（b）上层预测（Uplayer Prediction）。H.264标准中提供的块尺寸有16×16、8×16、16×8、8×8、8×4、4×8、4×4，它们的图像分割区域分别定义为搜索模式Mode1～Mode7。假设当前分割区域的预测模式为Mode_curr，上层模式Mode_up定义为：

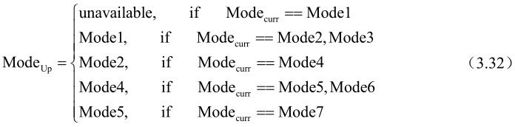
利用空间域上层搜索模式所得的最小SAD值作为当前模式下的预测SAD值的方法如图3.24所示。

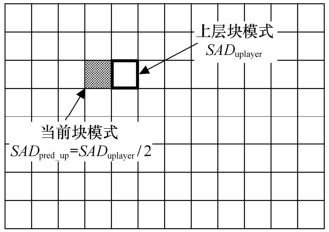
图3.24　SAD空间域上层预测模式

②匹配函数在时间域的预测方式。

（a）前帧对应块的预测（Corresponding-block Prediction）。利用前一帧中与当前块相同坐标位置的块在帧t′－1中搜索得到的最小SAD，作为当前搜索块在帧t′中进行搜索的SAD的预测值，如图3.25所示。

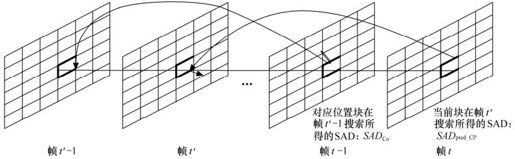
图3.25　SAD时间域前帧对应块预测模式

（b）时间域的邻近参考帧预测（Neighboring Reference-frame Prediction）。如图3.26所示，假设当前块所在帧的时间为t，则当在前面的参考帧t′中搜索时，可以利用当前块在参考帧t′＋1中搜索得到的最小SAD值SAD_NR作为当前块在帧t′搜索的SAD预测值，即

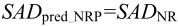
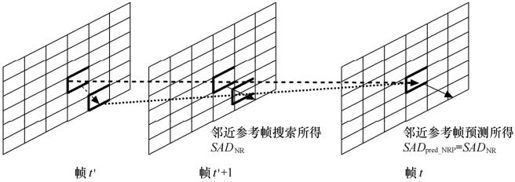
图3.26　SAD时间域邻近参考帧预测模式

以上所述的匹配误差的四种预测方式中，时间域的预测更为准确，其中邻近参考帧预测方式性能最优，这是由于在这种预测方式下当前块相同，邻近的参考帧之间具有较强的相关性。但是，它的性能受量化参数影响比较大，例如量化参数大的时候图像的细节模糊，相邻参考帧图像的内容之间的相似度增加，此时用邻近参考帧预测的方式会更为准确一些。

4．运动估计准则分类

运动搜索的目的就是在搜索窗内寻找与当前块最匹配的数据块，这样就存在着如何判断两个块是否匹配的问题，即如何定义一个匹配准则。而匹配准则的定义与运算复杂度和编码效率都是直接相关的，通常有如下几类比较常用的匹配函数的定义：

设当前帧为f₂，参考帧为f₁。

（1）最小均方差函数（MSE）

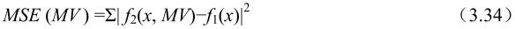
（2）最小平均绝对值误差（MAD）

等效于常用的绝对差值和（SAD）准则，性能很好，而且对硬件的要求相对简单，因而得到了最广泛的应用。

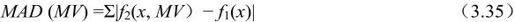
（3）阈值差别计数（NTD）

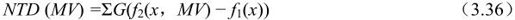
其中：

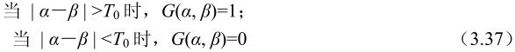
由于在用块匹配算法进行运动估计的过程中，利用匹配准则函数进行匹配误差的计算是最主要的计算量，因此，我们可以从这方面进一步减少计算量。由于图像的帧内也具有相关性，在计算误差匹配函数时，可以只让图像块中的部分像素参与运算，将块中的所有像素组成一个集合，那么参与计算的这部分像素集合就是它的子集，这种误差匹配的方法被称为子集匹配法。实验结果表明，在匹配误差无明显增加的情况下，采用子集匹配可以大大减少每帧图像的平均搜索时间。

5．运动搜索算法

匹配误差函数可以用各种优化方法进行最小化，这就需要我们开发出高效的运动搜索算法。主要的几种算法归纳如下。

（1）全局搜索算法

确定最优位移矢量的全局搜索算法方法是：在一个预先定义的搜索区域内，把当前帧的给定块与参考帧中的所有候选块进行比较，并且寻找具有最小匹配误差的一个。这两个块之间的位移就是所估计的MV，这样做带来的结果必然导致极大的计算量。

选择搜索区域一般是关于当前块对称的，左边和右边各有R_x个像素，上边和下边各有R_y个像素，如图3.27所示。

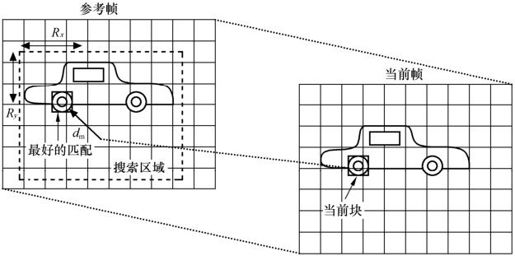
图3.27　全局搜索算法的搜索过程

如果已知在水平和垂直方向运动的动态范围是相同的，那么R_x＝R_y＝R。估计的精度是由搜索的步长决定的，步长是相邻两个候选块在水平或者垂直方向上的距离。通常，沿着两个方向使用相同的步长。在最简单的情况下，步长是一个像素，称为整数像素精度搜索，该种算法也称为无损搜索算法。

（2）分数精度搜索算法

由于在块匹配算法中搜索相应块的步长不一定是一个整数，一般来说，为了实现1/K像素步长，对参考帧必须进行K倍内插。图3.28给出了K＝2的例子，它被称为半像素精度搜索。实验证明，与整像素精度搜索相比，半像素精度搜索在估计精度上有很大的提高，特别是对于低清晰度视频。

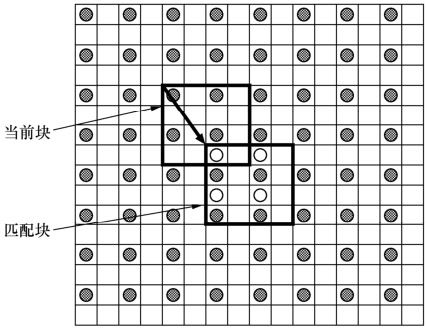
图3.28　半像素精度块匹配

但是，应用分数像素步长，搜索算法的复杂性大大增加。例如，使用半像素搜索，搜索点的总数是整数像素精度搜索的4倍以上。

如何确定适合运动估计的搜索步长，对于视频编码的帧间编码来说，就是要使得预测误差最小化。预测误差和搜索精度之间的关系的统计分析如图3.29所示。

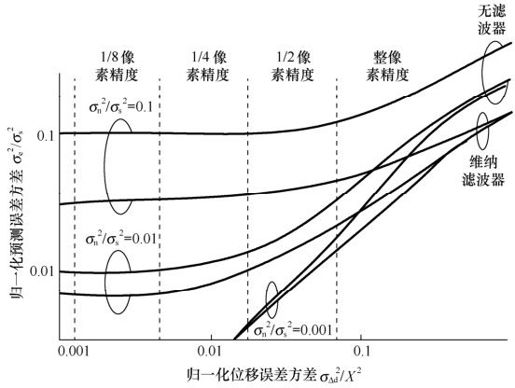
图3.29　运动补偿精度对有噪信号的预测误差方差的影响

可以看出，在低噪声情况下，需要不大于1/8像素的精度；而在高噪声情况下，1/2像素精度就够了。

（3）快速搜索算法

快速搜索算法和全局搜索算法相比，虽然只能得到次最佳的匹配结果，但在减少运算量方面效果显著。

①二维对数搜索法。这种算法的基本思路是采用大菱形搜索模式和小菱形搜索模式，步骤如图3.30所示，从相应于零位移的位置开始搜索，每一步试验菱形排列的五个搜索点。下一步，把中心移到前一步找到的最佳匹配点并重复菱形搜索。当最佳匹配点是中心点或是在最大搜索区域的边界上时，就减小搜索步长（菱形的半径），否则步长保持不变。当步长减小到一个像素时就到达了最后一步，并且在这最后一步检验9个搜索点。初始搜索步长一般设为最大搜索区域的一半。

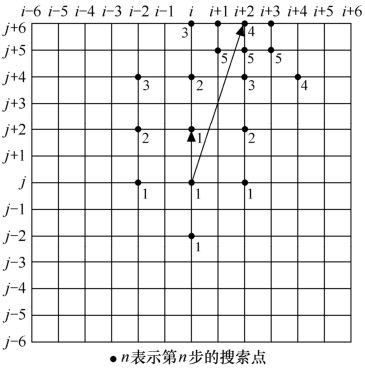
图3.30　二维对数搜索法

其后这类算法在搜索模式上又做了比较多的改进，在搜索模式上采用了矩形模式，还有六边形模式、十字形模式等。

②三步搜索法。如图3.31所示，这种搜索的步长从等于或者略大于最大搜索范围的一半开始。第一步，在起始点和周围八个“1”标出的点上计算匹配误差，如果最小匹配误差在起始点出现，则认为没有运动；第二步，以第一步中匹配误差最小的点（图中起始点箭头指向的“1”）为中心，计算以“2”标出的8个点处的匹配误差（注意，在每一步中搜索步长都比上一步长减少一半，以得到更准确的估计）；在第三步以后就能得到最终的估计结果，这时从搜索点到中心点的距离为一个像素。

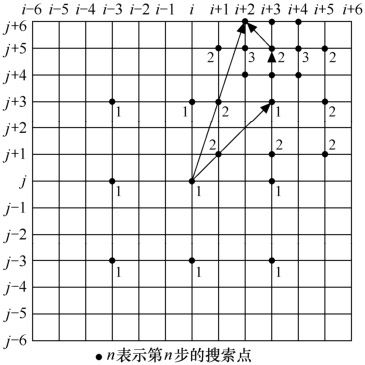
图3.31　三步搜索法

此外，本章的参考文献［6］中还提到了钻石搜索模型（Diamond search strategy）。

但是，上述一些快速算法更适合用于估计运动幅度比较大的场合，对于部分运动幅度小的场合，它们容易落入局部最小值而导致匹配精度很差，已经有很多各种各样的视频流证明了这一点。

针对这一缺点，国内外许多专家学者也提出了相应的应对措施，特别是针对H.264编码标准要求的一些快速算法的改进，并取得卓越的效果。例如本章参考文献［7］中提到的基于全局最小值具有自适应性的快速算法，这种算法通过在每一搜索步骤选择多个搜索结果，基于这些搜索结果之间的匹配误差的不同得到最佳搜索点，可以很好地解决落入局部最小值的问题。

本章的参考文献［8］中提到了一种适用于H.264的基于自适应搜索范围的快速运动估计算法，经过实验证明对于如salesman等中小运动序列，其速度可接近全局搜索算法的400倍，接近三步搜索算法的4倍；而对于大运动序列，如table tennis，该算法则会自动调节搜索点数以适应复杂的运动。当从总体上考察速度方面的性能时，可以看到，该算法平均速度是全局搜索算法的287.4倍，三步搜索的2.8倍。

（4）分级搜索范围（DSR）算法

分级搜索算法的基本思想是从最低分辨率开始，按精度逐级进行不断优化的运动搜索策略。如图3.32所示，首先取得两个原始图像帧的金子塔表示，从上到下分辨率逐级变细，从顶端开始，选择一个尺寸比较大的数据块进行一个比较粗略的运动搜索过程，在此基础上进行亚抽样（即通过降低数据块尺寸或提高抽样分辨率和减少搜索范围的办法），到下一个较细的级来细化运动矢量，而一个新的搜索过程可以在上一级搜索到的最优运动矢量的周围进行。在亚抽样的过程中也有着不同的抽样方式和抽样滤波器。这种方法的优点是运算量的下降比例比较大，而且搜索的比较全面；缺点是由于亚抽样或者滤波器的采用而使内存的需求增加，另外如果场景细节过多可能会落入局部最小点。

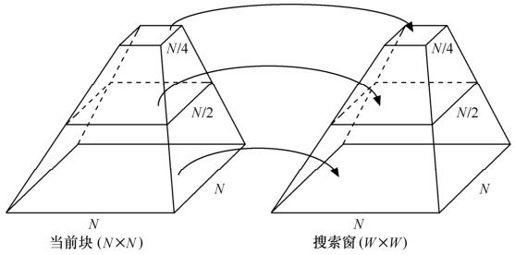
图3.32　分级运动搜索过程示意图

（5）混合搜索算法

由于物体的运动千变万化，很难用一种简单的模型去描述，也很难用一种单一的算法来搜索最佳运动矢量，因此实际上大多采用多种搜索算法相组合的办法，可以在很大程度上提高预测的有效性和鲁棒性，下面以图3.33为例说明。

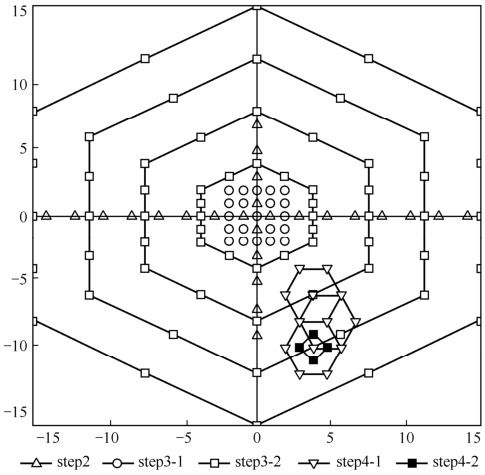
图3.33　非对称十字型多层次六边形格点运动搜索算法

具体搜索方法的步骤如下。

Step1：搜索过程的起始搜索点搜索

在起始搜索矢量的集合S中搜索一个对应费用函数值最小的候选运动矢量作为起始搜索点，费用函数表达式如下：

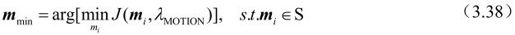
然后判断是否提前截止Early_Termination。

Step2：不对称的十字交叉搜索

由于自然界物体运动水平方向要比垂直方向剧烈一些，采用非对称的十字形搜索方法，搜索点集合为：

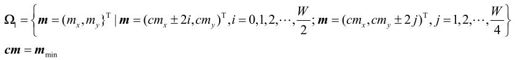
W为搜索区。

搜索步骤如下：

（1）

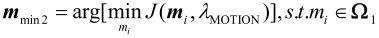
（2）

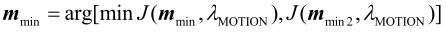
（3）Early_Termination

Step3：非均匀多层次六边形格点搜索，此步分成两个子步骤。

Step3-1：小矩形窗全搜索

定义候选运动矢量集合：

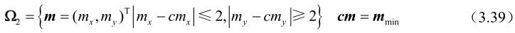
然后搜索步骤有：

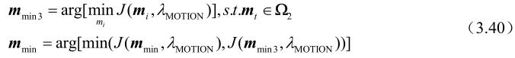
Early_Termination

Step3-2：扩展的多层次六边形格点搜索

六边形的16个点为：

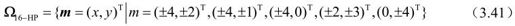
采用下列办法扩展搜索区：

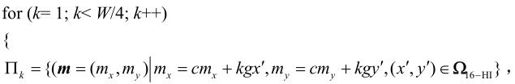
然后有：

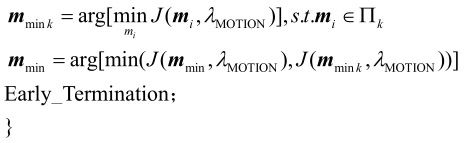
Step4：扩展的六边形搜索，分成两个子步骤：

Step4-1：六边形搜索模型定义为：

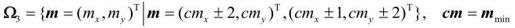
然后有：

如果m_min＝cm₂，跳转至Step4-2；

否则，跳转至Step4-1。

Step4-2：基于菱形模块的搜索

这一步骤的基本搜索模块为图3.33中所示的菱形模块，其集合为：

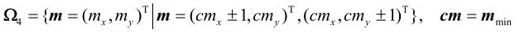
然后开始步骤如下：

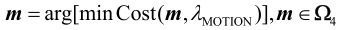
如果m_min＝cm，搜索截止

否则，跳转至Step4-2。

事实上，在运动估计时也并不是单一使用上述某一类搜索算法，而是根据各类算法的优点灵活组合采纳。在运动幅度比较大的情况下可以采用自适应的菱形搜索法和六边形搜索法，这样可以大大节省码率而图像质量并未有所下降。在运动图像非常复杂的情况下，采用全局搜索法，可在比特数相对来说增加不多的情况下使得图像质量得到保证。H.264编码标准草案推荐使用1/4分数像素精度搜索。本章的参考文献［6］中提到了在整像素搜索时采用非对称十字型多层次六边形格点运动搜索算法，然后采用钻石搜索模型来进行分数像素精度运动估计。

解码器要求传送的比特数最小化，而复杂的模型需要更多的比特数来传输运动矢量，而且易受噪声影响。因此，在提高视频的编码效率的技术中，运动补偿精度的提高和比特数最小化是相互矛盾的，这就需要我们在运动估计的准确性和表示运动所用的比特数之间作出折衷选择。它的效果与选用的运动模型是密切相关的。

3.2　变换编码

3.2.1　变换编码的基本概念

绝大多数图像都有一个共同的特征：平坦区域和内容缓慢变化区域占据一幅图像的大部分，而细节区域和内容突变区域则占小部分。也可以说，图像中直流和低频区占大部分，高频区占小部分。这样，空间域的图像变换到频域或所谓的变换域，会产生相关性很小的一些变换系数，并可对其进行压缩编码，即所谓的变换编码。

变换中有一类叫做正交变换，可用于图像编码。自1968年利用快速傅立叶变换（FFT）进行图像编码以来，出现了多种正交变换编码方法，如K-L变换、离散余弦变换（DCT）等。其中，编码编码性能以K-L变换最理想，但缺乏快速算法，且变换矩阵随图像而异，不同图像需计算不同的变换矩阵，因而只用来参考比较。DCT编码性能最接近于K-L变换，略次而已，但它具有快速算法，广泛应用于图像编码。

3.2.2　K-L变换

设一幅图像阵列每行由列矢量表示，即X＝(x₀, x₁,…,x_N-1)^T。由于图像内容的千变万化，该列矢量是随机矢量，用其平均值和协方差表征。

X的列矢量平均值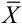为：

X的协方差矩阵定义为：

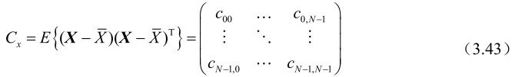
上式中，，表示随机变量x_i和x_j之间的相关程度的协方差（相关系数）。协方差矩阵对角线上的元素是各像素的方差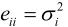，表示该像素的能量大小。

不难求出X的协方差矩阵C_x的特征值及其归一化特征矢量。利用这些特征矢量构成正交矩阵A，则图像X作正交变换后得：

该变换便是K-L变换，也叫做Hotelling变换。可以证明，Y的协方差矩阵是一个对角矩阵，其对角线上元素便是C_x的特征值。

这说明K-L变换后，Y中的相关性已全部消除，能量只集中在n个特征值λ_i上，其值按从大到小排列。因此编码只需传送前n个特征值，大大降低了码率。可以证明，在均方误差最小准则下，K-L变换是失真最小的变换。但K-L变换不易实现，只是一种理想的变换方法。

3.2.3　离散余弦变换（DCT）

1．一维DCT变换

DCT正变换时，设f(x)＝[f(0),f(1),…,f(N－1)]^T，对f变换后得：

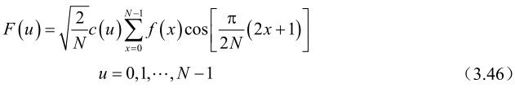
其中，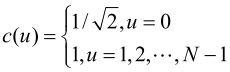

可写成矩阵形式：

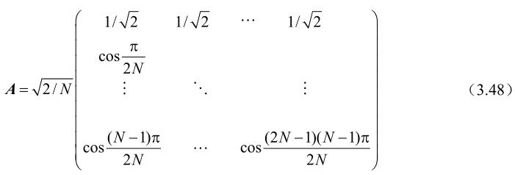
对应地，一维离散余弦反变换IDCT为：

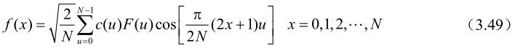
由于A^-1＝A^T，f可写成如下矩阵形式：

2．二维DCT变换

令f(x, y)为N×N离散图像序列，二维DCT变换表示为：

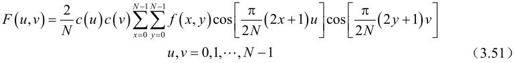
二维IDCT为：

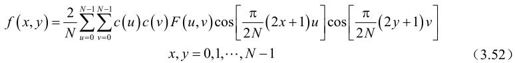
也可写成矩阵形式：

对于图像变换编码，最理想的变换操作应对整个图像进行，以便去除所有像素间的相关性，但这样的操作计算量太大。实际上，往往把图像分为若干块，以块为单位进行DCT变换。通常区16×16或8×8组成小块。

图像块通常只需用几个低频DCT系数表示，如图3.34所示。

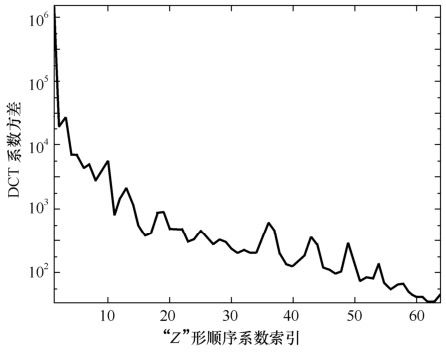
图3.34　8×8 DCT能量分布

由图3.35可见，每块用64个系数表示的图像，变换后只需用16个系数来表示原始图像。

左上图63各系数，右上图16个系数，左下图8个系数，右下图4个系数

图3.35　不同数目系数重建图像

3.2.4　锯齿形扫描和游程编码

变换系数量化后，在低频和直流区域有少量较大的值，高频区域有少量不大的值，系数大部分为零，为了更有效的编码，通常根据该统计特性采用熵编码进一步压缩码率。

熵编码之前，要进行锯齿形扫描和游程编码。

1．锯齿形扫描

以8×8块为例，量化后系数按图3.36所示的顺序进行锯齿形扫描，并排成一个串行数据序列。

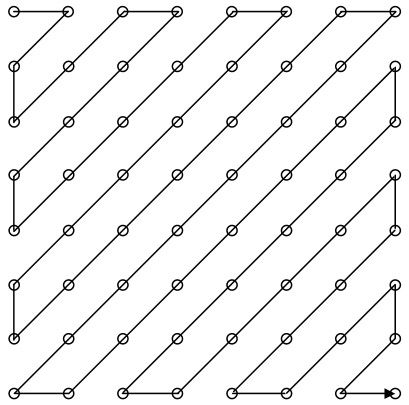
图3.36　锯齿形扫描

2．游程编码

在变换域，量化后系数用三个量表示，即0的个数（称为游程）、系数值和最后的位置。如非0系数已处于最后的位置或其后均为0，则置1，不然置0。现举例说明。

经锯齿形扫描后，得输入序列：

15，0，0，-3，4，5，0，0，0，0，-7，0，0，0…

则经游程编码后值为：

（0，15，0），（2，-3，0），（0，4，0），（0，5，0），（4，-7，1）

3.3　变换编码与预测编码的比较

由以上讨论可知，变换编码实现比较复杂，预测编码的实现相对容易，但预测编码的误差会扩散。以一行为例，由于后面的像素以前面的像素为参考，前面的像素的预测误差会逐步向后面的像素扩散。而且在二维预测时，误差会扩散至后面几行，形成区域误码。这样一来，对信道误码率的要求提高，一般要求不大于10^-6。相比之下，变换编码则不会误码扩散，其影响只限制在一个块内，而且反变换后误码会均匀分散到块内的各个像素上，对视觉无甚影响。这时信道误码率一般要求不大于10^-4即可。

两者各有优缺，特别是变换编码随着VLSI技术的飞跃发展，实现起来十分容易。现实中，往往采用混合编码方法，即对图像先进行带有运动补偿的帧间预测编码，再对预测后的残差信号进行DCT变换。这种混合编码方法已成为许多视频压缩编码国际标准的基本框架。

3.4　熵编码

利用信源的统计特性进行码率压缩的编码就称为熵编码，也叫统计编码。视频编码常用的有两种：变长编码（也称哈夫曼编码）和算术编码。现分别讨论其基本原理。

3.4.1　变长编码

1952年，哈夫曼提出变长编码方法：对出现概率大的符号分配短字长的二进制码，对出现概率小的符号分配长字长的二进制码，得到符号平均码长最短的码。变长编码也称为最佳编码。具体编码方法如图3.37所示。

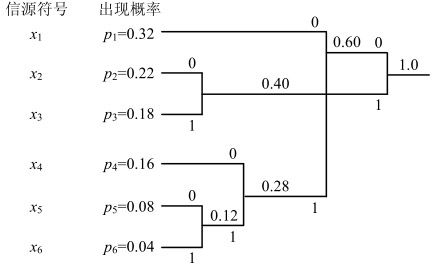
图3.37　哈夫曼编码举例

可得：

表3.2　　　　哈夫曼编码结果

则平均码长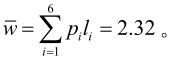

哈夫曼编码步骤如下：

第一步，将信息符号按其出现概率从大到小排列；

第二步，将两个最小概率组成一组，划成2个分支域，并标以0和1；再把2个分支域合并成1个支域，标以两个概率之和；

第三步，依次类推，直到概率之和等于1.0；

第四步，找出概率和1.0到各信息符号的路径，记下各路径从右到左各分支域的0和1，即得到信息符号相应的码字。

理论上，这种编码是最佳的。实际上，利用硬件实现时，出现概率的值不可能精确到小数后多少位，而最小存储单元为1bit，会引起概率匹配不准确及编码效率的下降。

3.4.2　算术编码

算术编码和哈夫曼编码不同，不采用一个码字代表一个输入信息符号的办法，而采用一个浮点数来代替一串输入符号，经算术编码后输出一个小于1，大于或等于0的浮点数，在解码端再进行正确地、唯一地解码，恢复原符号序列。举例如下。

设：输入序列为abaca，p(a)＝1/2，p(b)＝1/2，p(c)＝1/2，求算术编码输出序列。

解：

编码：

（1）列出各符号出现概率值，见表3.3。

表3.3　　　　符号出现概率

（2）在（0，1）区间内，每个字符根据其概率选定范围，见表3.3。

（3）开始时，浮点范围：R₀＝H₀－L₀＝1，H₀＝1，L₀＝0。

（4）当第一个字符“a”被传送时，其范围为[0.00,0.50]，H＝0.05，L＝0.00，可得发“a”字符的范围H和L：

L₁＝L₀＋R₀×L＝0.00

H₁＝L₀＋R₀×H＝0.50

范围R₁＝H₁－L₁＝0.50

对“a”编码后，编码范围从[0, 1）变为[0.00,0.50)。

（5）当第二个字符“b”被传送时，范围为[0.50,0.75)，H＝0.75，L＝0.50。

L₂＝L₁＋R₁×L＝0.25

H₂＝L₁＋R₁×H＝0.375

R₂＝H₂－L₂＝0.125

于是对“ab”编码后，编码范围从[0.00,0.50)变为[0.25,0.375)。

（6）依次类推：

最后输出码字为：0.3046875。

该例算术编码的结果见表3.4。

表3.4　　　　算术编码结果

解码：

（1）接收到浮点数0.3046875，对照表3.4，在范围H中查得第一个字符为“a”，其概率为0.5。

（2）从接收值减去“a”得的概率范围L，并除以p(a)，

（0.3046875－0.00）/0.5＝0.609375

该值为下一字符范围内的值。

（3）依此类推，解码出序列“abaca”。该例解码的结果见表3.5。

表3.5　　　　算术解码结果

参考文献

［1］毕厚杰．多媒体信息的传输与处理．北京：人民邮电出版社，1999.

［2］许志祥．数字电视与图像通信．上海：上海大学出版社，2000.

［3］Yao Wang, Jorn Ostermann, Ya-Qin Zhang. Video Processing and Communication. Pearson Education, 2002.

［4］Iain E.G.Richardon. H.264 and MPEG-4 Video Compression Video Coding for Next Generation Multimedia. Wiley Press，2003.

［5］Lloyd，P.S.. Least square quantization in PCM. IEEE Trans. Information Theory, March 1982: p127-135.

［6］Orchand M.T., G.J.Sulliran. OBMC. an estimation-theoretic approach. IEEE Trans Image Process, 1994(3): P693-699.

［7］陈志波．H.264运动估值与网络视频传输关键问题研究．北京：清华大学，毕业论文，2002.

［8］K. Venkatachalapathy, R. Krishnamoorthy, K. Viswanath. A new adaptive search strategy for fast block motion estimation algorithms. Journal of Visual Communication & Image Representation, 2004: 203-213.

［9］李翔，吴国威．一种适用于H.264的基于自适应搜索范围的快速运动估计算法．中国图像图形学报，2004(4):471-476.