13.5.4　Mahout中的聚类、分类算法

Mahout目前已经实现了Canopy聚类算法、K-Means聚类算法、Fuzzy K-Means聚类算法、Dirichlet过程聚类算法等众多聚类算法。除此之外，Mahout还实现了贝叶斯（Bayes）分类算法。这里主要介绍简单且应用广泛的K-Means聚类算法和贝叶斯分类算法。

K-Means聚类算法能轻松地对几乎所有的问题进行建模。K-Means聚类算法容易理解，并且能在并行计算机上很好地运行。学习K-Means聚类算法，能更容易理解聚类算法的缺点，以及其他算法对于特定数据的高效性。

K-Means聚类算法的K是聚类的数目，在算法中会强制要求用户输入。对于将新闻聚类成诸如政治、经济、文化等大类，可以选择10到20之间的数字作为K。因为这种顶级的类别数量是很小的。如果要对这些新闻详细分类，选择50到100之间的数字也是没有问题的。假设数据库中有一百万条新闻，如果想把这一百万条新闻按照新闻谈论的内容进行聚类，则这个聚类数目远远大于之前的聚类数目。因为每个聚类中的新闻数量不会太大。这就要求选择一个诸如10 000的聚类数值。聚类数值K的取值范围不定，它既可以小至几个，也可以大至几万个。这就对算法的伸缩性提出了很高的要求，而Mahout下实现的K-Means聚类算法就具有很好的伸缩性。

K-Means聚类算法主要可以分为三步。第一步是为待聚类的点寻找聚类中心；第二步是计算每个点到聚类中心的距离，将每个点聚类到离该点最近的聚类中去；第三步是计算聚类中所有点的坐标平均值，并将这个平均值作为新的聚类中心点。反复执行第二步，直到聚类中心不再进行大范围移动，或者聚类次数达到要求为止。

假设有n个点，需要将它们聚类成K个组。K-Means算法会以K个随机的中心点开始。算法反复执行上文中提到的第二步和第三步，直至终止条件得到满足。接下来以9个点为例，配以相应图示介绍K-Means算法。

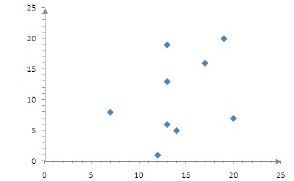
在聚类前，首先在二维平面中随机选择9个点，坐标分别为（7，8）、（12，1）、（13，6）、（13，13）、（13，19）、（14，5）、（17，16）、（19，20）、（20，7）。

1.第一次聚类

1）系统首先选取前3个点（7，8）、（12，1）、（13，6）作为聚类中心，然后计算每个点到聚类中心的距离，该点距离哪个聚类中心的距离最小就归属于哪个聚类中心。经过计算，点（7，8）、（13，19）为1个聚类，点（12，1）为1个聚类，点（13，6）、（13，13）、（14，5）、（17，16）、（19，20）、（20，7）为1个聚类，如图13-2所示。

图　13-2　未聚类的九个点

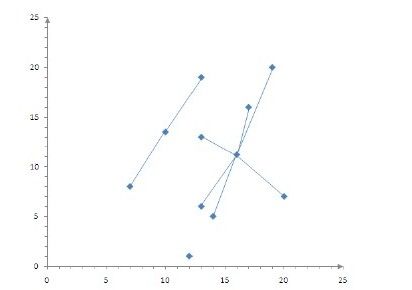
2）更新聚类的聚类中心，新的聚类中心的值为聚类中所有成员的平均值。聚类（7，8）、（13，19）的新聚类中心为（10.0，13.5），聚类（12，1）的新聚类中心仍为（12.0，1.0），聚类（13，6）、（13，13）、（14，5）、（17，16）、（19，20）、（20，7）的新聚类中心为（16.0，11.2），如图13-3所示。

图　13-3　一次聚类后的结果

2.第二次聚类

1）根据前面生成的聚类中心（10.0，13.5）、（12.0，1.0）、（16.0，11.2）重新计算每个点和聚类中心点之间的距离，根据计算出的距离对该点进行聚类。结果点（7，8）、（13，13）、（13，19）为1个聚类，点（12，1）、（13，6）、（14，5）为1个聚类，点（17，16）、（19，20）、（20，7）为1个聚类。

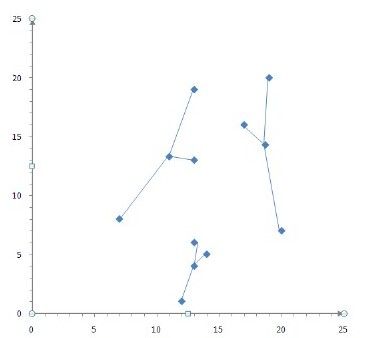
2）更新聚类的聚类中心，聚类（7，8）、（13，13）、（13，19）的新聚类中心为（11.0，13.3），聚类（12，1）、（13，6）、（14，5）的新聚类中心仍为（13.0，4.0），聚类（17，16）、（19，20）、（20，7）的新聚类中心为（18.7，14.3），如图13-4所示。

3.第三次聚类

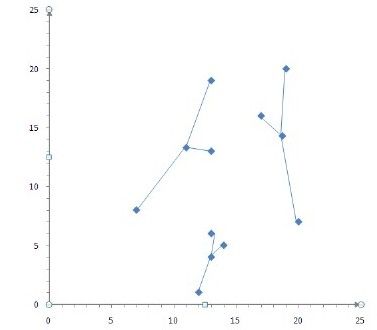
根据上一步来看，聚类结果没有发生变化，满足收敛条件，K-Means聚类结束，如图13-5所示。

介绍完K-Means聚类算法，下面开始介绍贝叶斯（Bayes）分类算法。贝叶斯（Bayes）分类算法是一种基于统计的分类方法，用来预测某个样本属于某个分类的概率有多大。贝叶斯（Bayes）分类算法是基于贝叶斯定理的分类算法。

贝叶斯分类算法有很多变种。在这里主要介绍朴素贝叶斯分类算法。何谓朴素？所谓朴素就是假设各属性之间是相互独立的。经过研究发现，大多数情况下，朴素贝叶斯分类算法（Naïve Bayes Classifier）在性能上和决策树（Decision Tree）、神经网络（Netural Network）相当。当针对大数据集的应用时，贝叶斯分类算法具有方法简单、高准确率和高速度的优点。但事实上，贝叶斯分类算法也有其缺点。缺点就是贝叶斯定理假设一个属性值对给定类的影响独立于其他属性的值，而此假设在实际情况中经常是不成立的，因此其分类准确率可能会下降。

图　13-4　二次聚类后结果

图　13-5　第三次聚类的结果

朴素贝叶斯分类算法是一种监督学习算法，使用朴素贝叶斯分类算法对文本进行分类，主要有两种模型，即多项式模型（multinomial model）和伯努利模型（Bernoulli model）。Mahout实现的贝叶斯分类算法使用的是多项式模型。对算法具体内容感兴趣的读者可以阅读http：//people.csail.mit.edu/jrennie/papers/icml03-nb.pdf上的论文^[1]。本书将以一个实际的例子来简略介绍使用多项式模型的朴素贝叶斯分类（Naïve Bayes Classifier）算法。

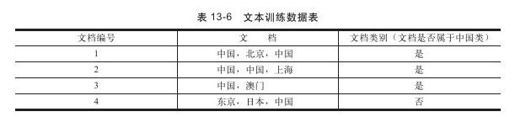
给定一组分类号的文本训练数据，如表13-6所示。

给定一个新的文档样本“中国、中国、中国、东京、日本”，对该样本进行分类。该文本属性向量可以表示为d=（中国，中国，中国，东京，日本），类别集合Y={是，否}。类别“是”下共有8个单词，“否”类别下面共有3个单词。训练样本单词总数为11。因此P（是）=8/11，P（否）=3/11。

类条件概率计算如下：

P（中国|是）=（5+1）/（8+6）=6/14=3/7；

P（日本|是）=P（东京|是）=（0+1）/（8+6）=1/14；

P（中国|否）=（1+1）/（3+6）=2/9；

P（日本|否）=P（东京|否）=（1+1）/（3+6）=2/9。

上面4条语句分母中的8，是指“是”类别下训练样本的单词总数，6是指训练样本有中国，北京，上海，澳门，东京，日本，共6个单词，3是指“否”类别下共有3个单词。有了以上的类条件概率，开始计算后验概率：

P（是|d）=（3/7）3×1/14×1/14×8/11=108/184877≈0.00058417；

P（否|d）=（2/9）3×2/9×2/9×3/11=32/216513≈0.00014780。

因此，这个文档属于类别中国。这就是Mahout实现的贝叶斯（Bayes）分类算法的主要思想。

[1]　Trackling the Poor Assumptions of Naive Bayes Text classifiers.