13.6.3　简单分布式系统下基于产品的推荐系统简介

传统的推荐引擎算法多在单机上实现，它们只能处理一定量的数据。如果数据量达到一定的规模，传统的推荐引擎算法就会出现各种问题。

在传统的推荐算法中，算法会将用户喜欢的产品抽象成三个具体的数值：用户编号、产品编号和喜爱值。这里的喜爱值表示用户对产品的喜爱程度，它可以用一个具体数值来表示。例如，可以使用1到5来表示喜欢的程度：1表示非常不喜欢；2表示不喜欢；3表示没有任何感觉；4表示喜欢；5表示非常喜欢。也可以从1到5都表示喜欢，数值越大代表越喜欢。然后通过计算产品之间的相似性来向用户推荐产品。

分布式系统没有使用这种方法。分布式系统下的推荐算法主要包括以下几部分：

计算表示产品相似性的矩阵。

计算表示用户喜好的向量。

计算矩阵与向量的乘积，为用户推荐产品。

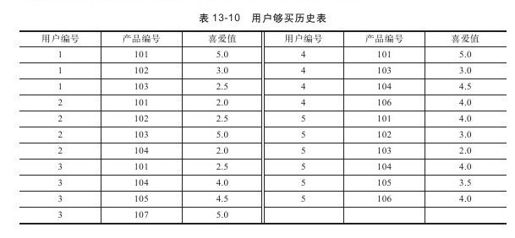
在开始介绍推荐算法之前，首先建立一组数据，如表13-10所示。在这组数据中，每条记录包含三个信息：用户编号、产品编号、用户对产品的喜爱值。

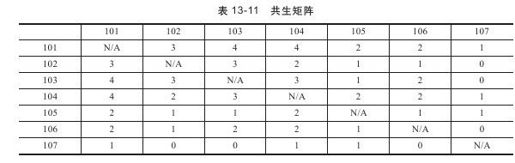
表13-10显示了5名顾客的购买历史。下面来介绍一种方法：使用共生矩阵来表示产品的相似性。在这里，产品的相似性是指产品出现在一起的次数。例如从表13-10中可以看出产品101和产品102一共出现过三次，分别是在用户1、用户2、用户5的物品清单上。那么在共生矩阵中101和102对应的元素值就应该为3。经过统计表13-10中的5个用户的购物清单可以使用表13-11的矩阵来表示。

表13-11中的行和列都是产品的编号。观察可知，该矩阵是一个对称矩阵。在计算过程中可以使用一些特殊技术对矩阵进行处理，使得程序的效率更高。原因是产品104和产品105出现的次数与产品105和产品104出现的次数必然是相同的。在共生矩阵中对角线的元素是没有意义的。计算时可以使用0进行代替。

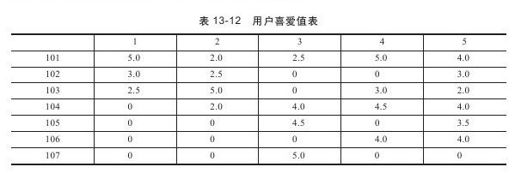
除了共生矩阵外，还需要一个表示用户喜好的向量。在该向量中，对于用户购买过的产品必然会有一个表示喜好的数值，对于用户没有购买的产品，选择用数字0来表示该用户对该产品没有任何喜好。例如对于用户4而言，他的向量就应该是（5.0，0，3.0，4.5，0，4.0，0）。通过计算可以得到所有用户的喜爱值，如表13-12所示。

其实该表也是一个矩阵：矩阵的行值是产品编号，列值是用户编号，行列对应的元素值为用户对产品的喜爱值。通过观察可以发现，矩阵中包含很多0，这种矩阵可以称为稀疏矩阵。对于稀疏矩阵，同样可以采用一些技术手段使程序效率更高。

既然已表示了产品的相似性，也表示了用户对产品的喜爱，剩下的就是如何计算推荐的产品了。其实这很简单，只要将共生矩阵与用户的列向量相乘得到一个新的列向量即可。在新的列向量中，所有可以推荐产品对应的值最大，就是计算得到的推荐产品。

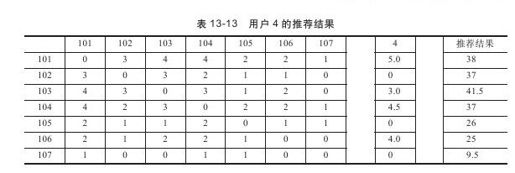
以向用户4推荐产品为例，如表13-13所示。

从结果可以看出，用户最喜欢产品103，但是103已经买过，因此无须推荐该产品。同理101、104、106也都可以不推荐。在可以推荐的产品102、105、107中，选择推荐产品102。因为102的计算机结果是三者之中最大的。

推荐结果已经有了，下面来分析这个结果是否合理。在所有可以推荐的产品中，推荐引擎选择了计算结果最大的产品。为什么计算结果最大的产品就是最合理的推荐产品呢？

回想整个计算过程。在计算结果中处在第2行的计算结果37是矩阵第2行元素和用户4的列向量的乘积，3×（5.0）+0×0+3×3+2×（4.5）+1×0+1×（4.0）+0×0=37。矩阵中的第2行表示的是所有产品和产品102同时出现的次数。如果用户对某个产品非常喜欢，而这个产品又和产品102同时出现的次数很多，那么乘积对计算结果的影响就会较大。这刚好就是推荐引擎要达到的目的，用户非常喜欢的产品和102很相似，推荐引擎可向用户推荐该产品。

对于大量数据，计算结果会非常大。但是没有关系，推荐引擎关注的是所有结果的大小关系，而不是具体的数值。因为最终向用户推荐的是可以推荐产品中计算结果最大的。在计算的过程中，对于不是最大的计算结果以及用户已经购买过的产品，推荐引擎无须推荐，因此也不必计算它们的结果。

通过分析可知，推荐引擎计算出的推荐结果是合理的。但为什么它适合大规模的数据呢？下面来说明这个问题。在计算共生矩阵的时候，每次只需考虑一个向量；在计算用户向量的时候只需考虑该用户的喜好；在计算推荐结果的时候只需考虑矩阵中的一列值。这都表明，这个方法可以使用MapReduce编程模式。