附录A 二进制和十六进制

对使用 C++编写更好的应用程序来说，理解二进制和十六进制的工作原理并非至关重要，但这有助于更深入地了解幕后发生的情况。

A.1 十进制

我们日常使用的数字用0～9表示，这种数字被称为十进制数。十进制使用10个不同的数字，其基数为10。

基数为10时，如果从零开始对各位进行编号，则每位表示的值为该位的数字乘以10 ^编号，因此：

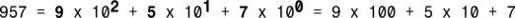
在数字957中，7对应的位编号为0，5对应的位编号为1，9对应的位编号为2。这些位编号将用作以10为底的指数，如上述示例所示。别忘了，任何数的零次方都为1，因此10⁰和1000⁰的值相同，都是1。

对十进制来说，10的幂很重要。在十进制数中，各位的量级分别是10、100、1000等。

A.2 二进制

二进制的基数为2。在二进制中，每位只有两种可能的状态，用数字0和1表示。在C++中，0和1分别对应于false和true（true为非零值）。

就像十进制数是根据10的幂计算其表示的值一样，二进制数根据2的幂计算其表示的值：

101₂ = 1×2² + 0×2¹+ 1×2⁰ = 4 + 0 + 1 = 5₁₀

因此，二进制数101对应的十进制数为5。

在二进制数中，各位的量级2的幂，即分别是4、8、16、32等。其中，指数为当前位的编号，而编号从零开始。

为更深入地了解二进制，请看表A.1，其中列出了2的幂。

表A.1 2的幂

续表

A.2.1 计算机为何使用二进制

二进制广泛使用的历史较短，电子学和计算机的发展使其应用得以普及。电子学和电子元件的发展导致了一个新系统，它将元件状态视为ON（高电平）或OFF（低电平）。

ON和OFF状态非常适合使用1和0来表示，而这正是二进制使用的数字，因此二进制可用于算术计算。通过开发电子门，很容易支持第5章介绍的逻辑运算，如NOT、AND、OR和XOR，这使得使用二进制进行条件处理很容易。

A.2.2 位和字节

位是计算系统中基本单位，包含一个二值状态。因此，如果位包含状态1，则称为被“设置”，如果包含状态0，则称为被“重置”。一系列位称为字节；从理论上说，一个字节包含的位数并非固定的，它随硬件而异。

然而，大多数计算系统都假定一个字节包含8位，这是处于简单和方便的考虑，因为8为2³。由于一个字节包含8位，因此能存储2⁸（256）个不同的值，这足以表示ASCII字符集中的所有字符。

A.2.3 1KB相当于多少字节

1KB为1024（2¹⁰）字节。同样，1MB为1024KB，1GB为1024MB，1TB为1024GB。

A.3 十六进制

十六进制的基数为16。在十六进制中，各位的值用0-9和A-F表示，因此十进制数10对应的十六进制值为A，十进制数15对应的十六进制值为F：

在十进制中，各位的量级为10的幂，而在二进制中，各位的量级为2的幂；同样，在十六进制中，各位的量级为16的幂：

0x31F＝3×16² + 1×16¹ + F×16⁰ = 3×256 + 16 + 15 = 799₁₀

根据约定，使用前缀0x表示十六进制数。

A.3.1 为何需要十六进制

计算机使用二进制。在计算机中，每个内存单元的状态为 0 或 1。然而，如果人类在计算机中使用0和1来表示编程信息，则表示少量信息就需大量空间。因此，如果不使用二进制值1111，而使用十六进制值F，效率将高得多。

每个十六进制位可表示 4 个二进制位，因此使用两个十六进制位就能表示一个字节的状态，其效率非常高。

另一种进制是八进制，用得较少。八进制的基数为8，每位用数字0～7表示。

A.4 不同进制之间的转换

处理数字时，您可能需要用不同的进制表示同一个数字，如二进制值的十进制表示或十进制数的十六进制表示。

前面的示例演示了如何将二进制数或十六进制数转换为十进制数，下面来看看如何将十进制数转换为二进制和十六进制。

A.4.1 通用转换步骤

在不同进制之间进行转换时，将从要转换的数字开始，不断地除以目标基数，并从最右边开始，不断将余数填入目标数中。下一次执行除法运算时，将前一次除法运算的商作为被除数，并将目标基数作为除数。

这个过程将不断持续下去，直到余数可用目标进制的一位表示，且商为零。

这种方法也被称为分解法（breakdown method）。

A.4.2 从十进制转换为二进制

要将十进制数33转换为二进制，步骤如下：

第1位：将33除以2，商为16，余数为1

第2位：将16除以2，商为8，余数为0

第3位：将8除以2，商为4，余数为0

第4位：将4除以2，商为2，余数为0

第5位：将2除以2，商为1，余数为0

第6位：将1除以2，商为0，余数为1

因此十进制数33的二进制表示为：100001。

同样，要将十进制数156转换为二进制，步骤如下：

第1位：将156除以2，商为78，余数为0

第2位：将78除以2，商为39，余数为0

第3位：将39除以2，商为19，余数为1

第4位：将19除以2，商为9，余数为1

第5位：将9除以2，商为4，余数为1

第6位：将4除以2，商为2，余数为0

第7位：将2除以2，商为1，余数为0

第8位：将1除以2，商为0，余数为1

因此十进制数156的二进制表示为：10011100。

A.4.3 从十进制转换为十六进制

步骤与转换为二进制相同，但除以基数16，而不是2。

因此，要将十进制数5211转换为十六进制，步骤如下：

第1位：将5211除以16，商为325，余数为11（对应的十六进制数为B）

第2位：将325除以16，商为20，余数为5

第3位：将20除以16，商为1，余数为4

第4位：将1除以16，商为0，余数为1

因此十进制数5211的二进制表示为：145B。

要更深入地了解各种进制的工作原理，可编写一个类似于程序清单27.1的简单C++程序，在其中使用std::cout和控制符显示一个整数的十六进制、十进制和八进制表示。

要显示整数的二进制表示，可使用第25章介绍的std::bitset，并参阅程序清单25.1。