三、古希腊奇葩说(下)

上篇咱们聊到，古希腊脱口秀之王亚里士多德，提出了个奇葩的理论，他认为万物的本原是—— 水、火、土、气

他认为气和火轻，飘在大地上方、月球下方。

土和水重，有朝地心下落的趋势，二者构成了大地。

原本在讨论世界上最小的东西是啥，可一不留神，就扯出了另一个终极命题：

发现没？咱们思考问题通常都是天马行空，古希腊人却很有章法，要抓，就抓两头。

而从这个大问题延伸出去，就引出了在科学史上掀起腥风血雨的—— 地心说

虽然现在看来，地心说完全不靠谱。

但如果你足够了解它，你会发现，地心说不仅是一个科学理论，还是人类最早成体系的科学理论之一。

要了解地心说，我们只讲三个人就够了。

我们可以亲切地把这三位大佬称为：古希腊“完美”三剑客。

一、古希腊的“毕姥爷”

首先，有请我们的第一位主角，古希腊的“毕姥爷”——

老毕，辈分高，水平也高，是个有头有脸的人物，所以他创立的毕达哥拉斯学派，门徒众多，是古希腊四大门派之一。

作为学界的意见领袖，他也曾被问过关于世界本原的问题，而他的回答，在清奇中透露出一种俏皮：

万物的本原是数。

一片，他爱我；

两片，他不爱我……

老毕这个回答其实很有想法，因为他已经摆脱了事物的外在，直接抓住了本质，这被称为抽象思维。

老毕作为数学的宗师，搞出过许多高冷的数学理论。比如他证明了：

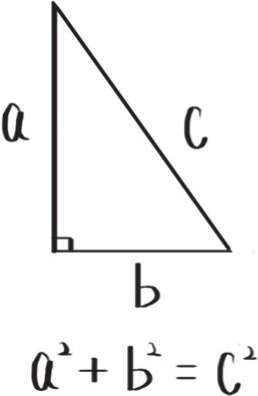
勾股定理

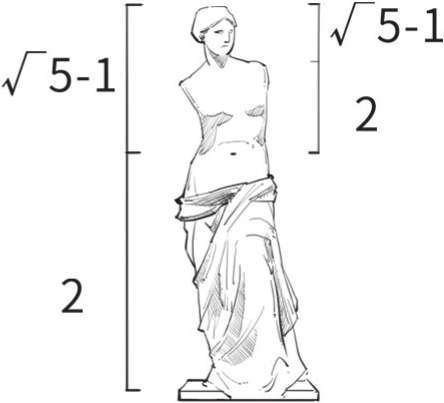
黄金分割

因此，勾股定理也叫作：

毕达哥拉斯定理

这个定理还引发了第一次数学危机。具体是咋回事呢？据说，有天老毕正在给学员们讲课……

其中有个熊孩子，提出了一个问题，角度十分刁钻，直接把老毕整蒙了!

当时的古希腊，还没有无理数的概念。

这一下就触及到了老毕的知识盲区，眼看苦心经营的完美形象濒临瓦解，不行!消灭!必须消灭!

接着，他就把提问的同学给消灭了……

由勾股定理引发的这次危机，就被称为第一次数学危机，也称为有理数危机。现在我们知道这答案是。

虽然这事儿只是个传说，但也反映出毕姥爷很可能是个处女座，有完美主义倾向。

也正是这种完美主义，让他提出了另一个更大胆的猜想—— 大地是圆的!

据说他的逻辑是这样的：

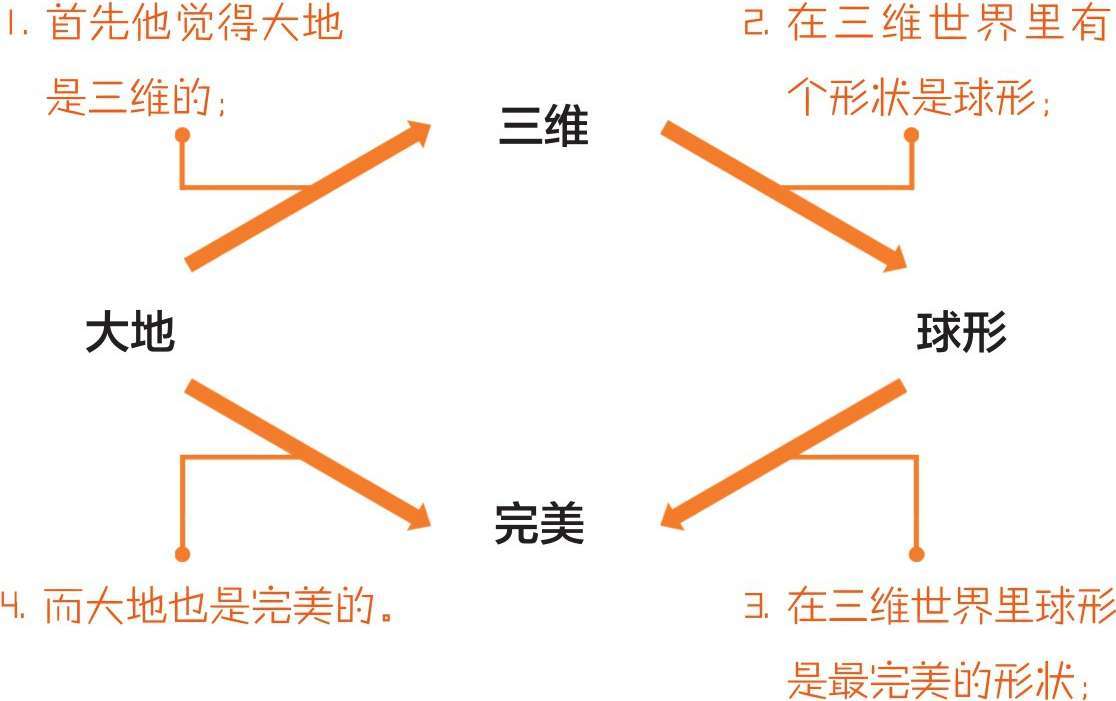
所以根据这些条件……

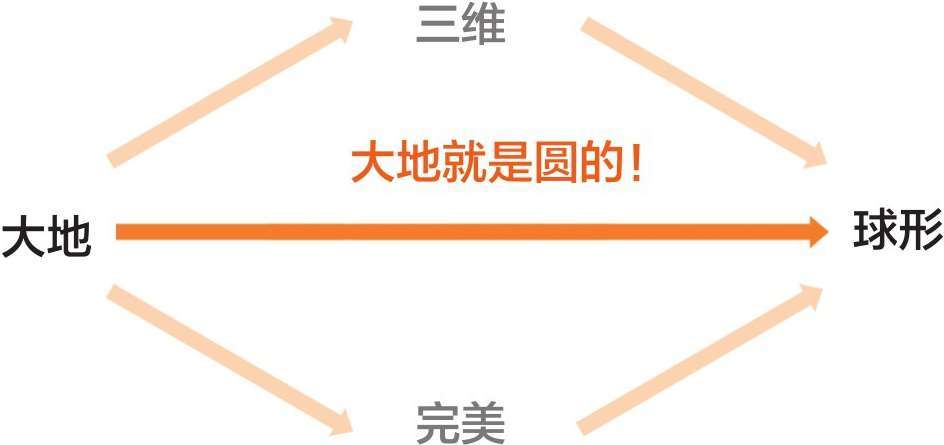
老毕不仅觉得地球完美，还觉得整个宇宙也很完美。

于是他又发了条微博，说整个宇宙也是一个大球体。宇宙中心是一团中心火，所有的天体都绕着中心火转。他还假想出一个天体：对地。

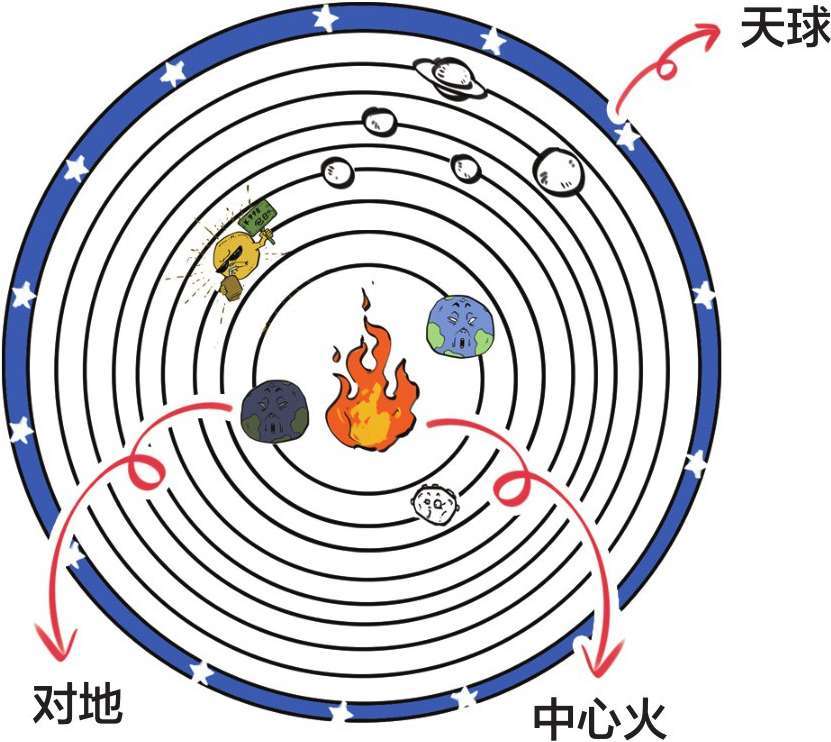
毕达哥拉斯认为数字10是完美的，因此，应该有10个会动的天体，但实际观测到的却没有10个，于是他硬编出个“对地”来凑数。

当然，这些理论也不全是他一个人提出来的，准确地说，应该是毕达哥拉斯学派提出来的。

由此可以看出，老毕绝对是个完美主义者，正是由于他的影响，在以后相当长的时间里，古希腊人都和完美杠上了。

二、古希腊的大学霸

老毕之后，古希腊相继出现了许多武林高手，其中吵得最欢的一个叫苏格拉底，他还有个徒弟叫柏拉图。

这个柏拉图和老毕一个德行：崇尚完美。他觉得，光是宇宙的形状完美还不够，每个天体的运动也必须完美。

于是，他提出天体的运动也是完美的——

其实柏拉图也注意到了理论和观测不相符的问题，于是，他发起了一项竞猜活动：拯救现象。

说白了，柏拉图的意思就是：我的想法没有错，只是还不够完善。

在柏拉图的号召下，大家就开始用匀速圆周运动组合各种模型。

其中有个叫欧多克斯的，提出了一个还凑合的方案—— 同心球叠加模型

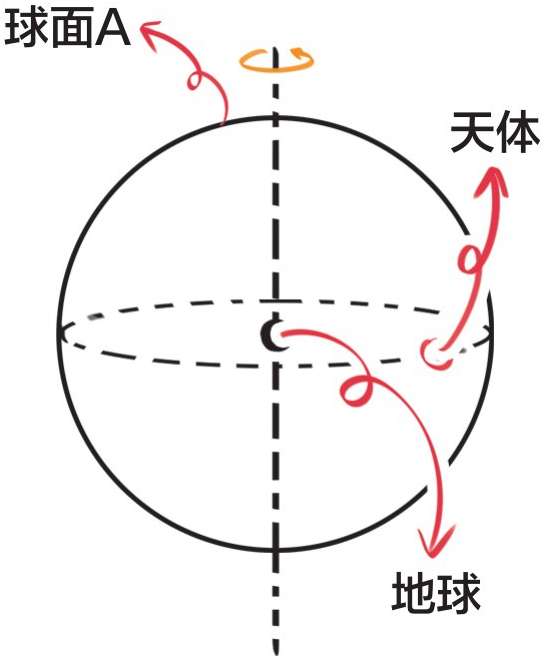
1. 地球是宇宙的中心，且地球是静止不动的；

2. 地球外套着一个球面A，球面A与地球同心，称为同心球，且同心球自身绕轴旋转；

3. 天体沿同心球的赤道运动。

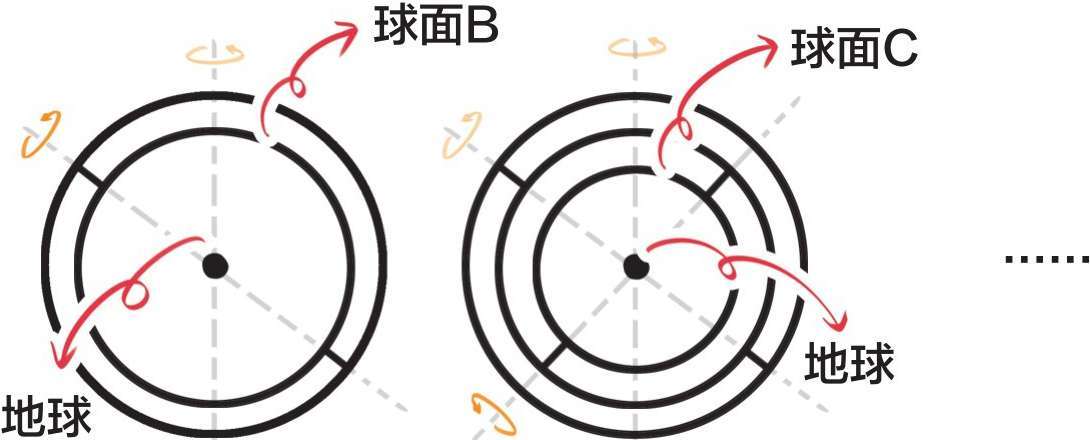
地球不止嵌套一个同心球，而是有很多同心球，一圈套一圈。比如球面B、球面C……以此类推，大概有27个同心球。

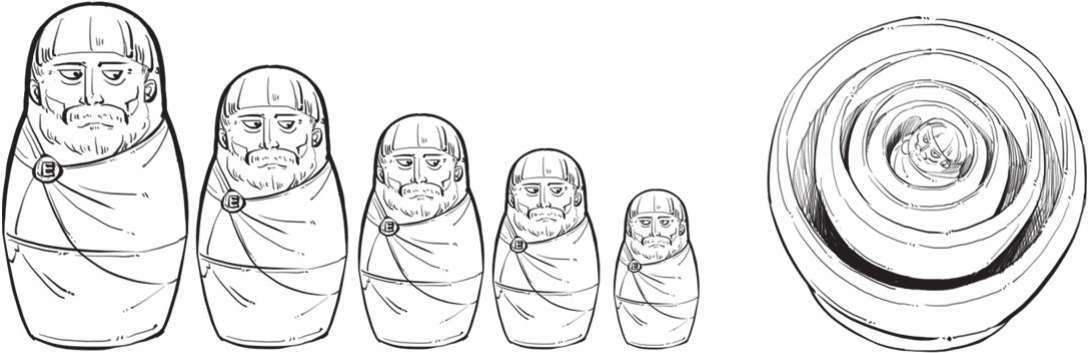
这个理论很复杂，也早就过时了，为了不浪费大家的脑细胞，就打个简单的比方：它其实就像俄罗斯套娃，一层套一层，为的就是让理论和现象能匹配。

“地球位于宇宙中心”是欧多克斯提出来的，这就是地心说1.0版。

在这之前，大家并不关心天体的运动，欧多克斯之后，大家开始想给天体排日程表，其实就是想预测天体的运动。

如果非要用一句话概括欧多克斯模型的意义，那应该是：从这时开始，古希腊的杠头们开始接地气了。

这就好比射箭，欧多克斯之前，比的是谁的动作更酷；欧多克斯之后，比的是谁射得更准。

现在，我们要请出古希腊的大学霸了，他也是柏拉图的徒弟，欧多克斯的师兄弟，我们熟悉的亚里士多德。

前面我们提到，小亚在讨论万物本原时，实现了一次称霸，现在聊到了宇宙，他当然也不能落后。要实现这个目标，就得完成两件事：

1.证明大地是球形的

首先，小亚为了让大家相信大地是球形的，他找到了几个关键证据。

证据一：

夜晚的时候，一直朝着北极星走，前方会出现一些新的星星，而后方的一些星星会消失。

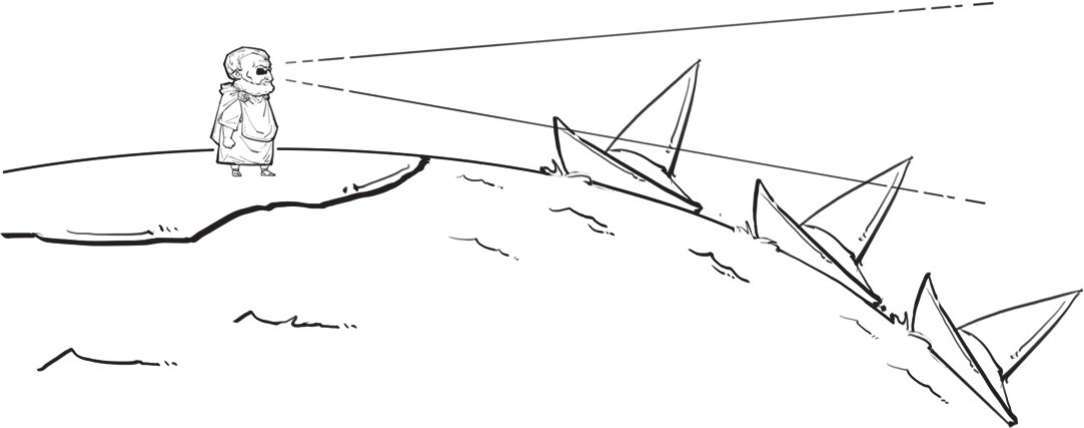
证据二：

大海里的帆船，靠近时先出现船帆，后出现船身；离去时，船身先消失，船帆后消失。

证据三：

月食的时候，大地投射在月亮上的影子是弓形的。

亚里士多德为了证明大地是球形的，使用了罗列观测证据的方法，这是人类第一次使用这种方法，它打开了实证科学的大门。

2.提出水晶球模型

大家还记得前面欧多克斯的27个同心球吧，小亚作为一个很有想法的人，思前想后，决定再加几个，这一加就是22个。

他的模型被我们称为水晶球模型。

但他这样做不是为了让天体的日程表更准确，而是为了解释天体为什么会运动。

让我们通过下面这张图来体会一下小亚的想法有多高端。

“水晶球模型”就是地心说2.0版。

亚里士多德的水晶球模型，不再局限于追求理论和各个天体运动现象的吻合，而是开始尝试了解天体之间的相互关系。

三、古希腊的人工智能

亚里士多德之后，小伙伴们沿着柏拉图“拯救现象”的精神继续探索。也就是说，他们正朝着“更准”的方向努力。

当时的人们发现，五大行星的行踪，就像姑娘的心思一样难以琢磨，一会儿向左，一会儿向右；一会儿变亮，一会儿变暗。

糟心的是，同心球理论并不能解决这个问题。

五大行星就是我们熟悉的金、木水、火、土这五颗行星。

不久之后，一个叫作阿波罗尼的人提出了本轮和均轮的概念，来补充地心说模型。

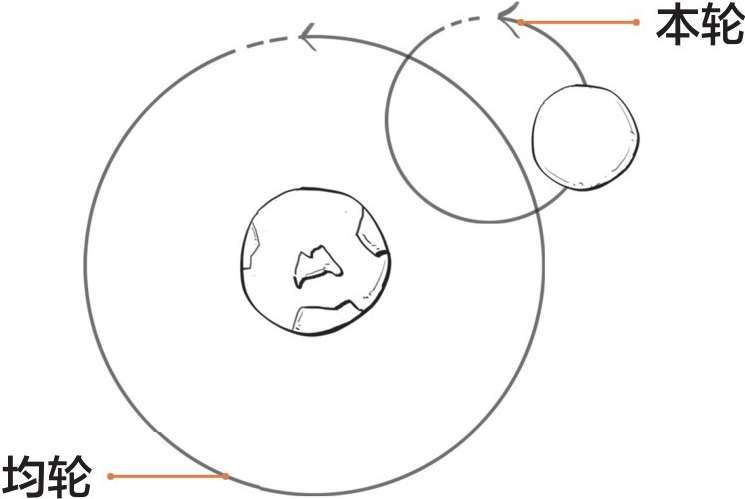
后来，又有一个叫作喜帕恰斯的人提出：如果地球不在太阳圆周运动的中心点上，而是处于一个偏心的位置上，模型会更加准确。

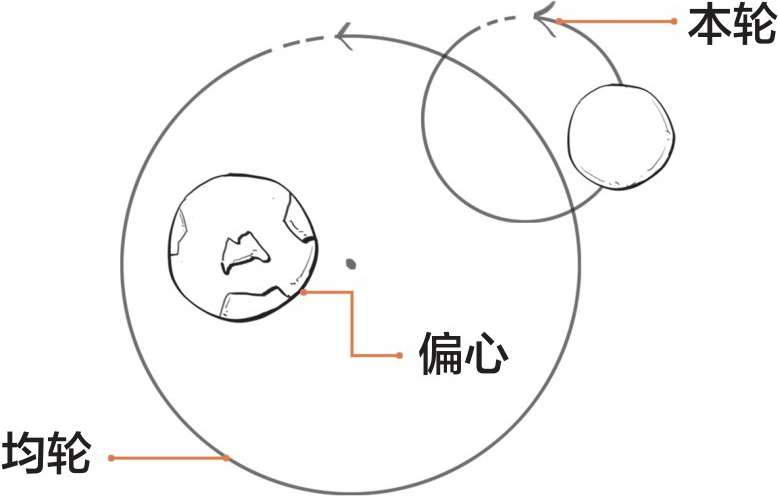
这里要强调一下，这时的人们仍然相信地球是宇宙的中心，只不过它不在均轮的中心而已。

最后，把地心说进行完善和推广的是托·古希腊人工智能·勒密。

其实他干了一件亚里士多德干过的事，也就是之前提到过的老三步—— 第一步：大量学习前人理论，并进行系统性总结。

第二步：在前人的理论基础上加入自己的想法，并根据实际观测结果不断校正理论。

第三步：提出系统的地心说模型，出版巨著《天文学大成》，也叫《至大论》。

“托勒密的地心说”就是地心说3.0版，也是终极版本。

这本书横行西方天文学界一千多年，是那些年里的标准教科书。

托勒密这套系统最难能可贵之处，在于其引入了大量数学方法进行论证。

在那个没有计算机的年代，托勒密就已经在搞大数据运算了，关键是还算得贼准，完全就是一个行走的人工智能。

经过几代学者的折腾，地心说得到了一次次升级，用地心说对天文现象做预测，已经可以做到很准确了，至少对于那个时代而言已经完全够用了。

很多人认为地心说算不上科学理论。这种理解其实并不正确，实际上地心说符合科学理论的基本要求：

请看下篇：

古希腊另类杠头集锦