四、古希腊另类杠头集锦

古希腊奇葩超级多，但在茫茫葩海中，还有两位另类杠头，我们绝对不能错过。

几何之父

欧几里得

力学之父

阿基米德

两位大佬对科学做出了巨大贡献，影响力持续至今，他们的理论是初中数学和物理的重点内容。

冤有头，债有主，是不是依稀想起当年被这两门学科支配的恐惧了？

嘴上随便突突，刀下冤魂无数，堪称史诗级刽子手。

所以这篇，咱们就来好好认识一下这两人。

一、欧几里得

据说小欧是个好学的孩子，年轻时候的梦想，就是去柏拉图学园深造。

柏拉图学园是图哥创立的学术圣地，以分数线高、招生严格著称。学园门口常年竖着一块木牌，上面满是对文科生深深的恶意：“不懂几何者，不得入内!”

面对这样一条铁律，无数学子只能默默流泪。

就在众人望而却步之时，人群中的欧几里得却暗自窃喜。

原来，小欧偏科严重，是几何界的顶级学霸。

于是他一个箭步，直接溜进学园!这个故事也告诉我们一个道理—— 三分靠努力，七分靠押题!

爱蒙才会赢!

每个学有所成的学子，都有个一线城市梦，欧几里得也一样。

毕业后，小欧决心做个亚漂，他来到了古希腊文化最发达的地方——亚历山大城。

到底多有文化呢？

据说那里的人对知识的渴望，已经到了丧心病狂的程度。如果你家财万贯，没人会搭理你，但假如你带着一本书上街，那你甚至可能会被官方打劫。

接着他们会找人把你这本书抄一遍，然后把誊抄的版本给你，原本则收入他们的图书馆中。

所以，在亚历山大城生活的日子里，欧几里得简直如鱼得水。

而且他还搞了件大事，套路和亚里士多德很像。

Step 1：

搜集整理以前的数学知识，并向数学大神们请教。

Step 2：

在原来知识的基础上，加一些自己的创新。

Step 3：

写出史上最成功的教科书——《几何原本》。

这本书瞬间就冲上了各种榜单，成为现象级畅销书，连国王都变身为欧粉。

虽然国王也是学霸，但在几何里却栽了跟头，于是他偷偷溜到欧几里得面前，求取真经。

于是就有了这样一条千古流传的学习箴言：

“在几何学里，

没有专为国王铺设的大道。”

——欧几里得

翻译成大白话就是：

学习得一点一点啃！

头发得一根一根掉！

除此之外，《几何原本》最厉害的地方在于，它用到了—— 公理化方法

举例来讲：

首先，《几何原本》里有23条最基本的定义，用以说明点、线、面、圆、角等是什么；

其次，还有5条公设，比如点到点可作一条直线。

接着，从这些定义和公设出发，推理演绎出一些结论，比如三角形内角和为180度。

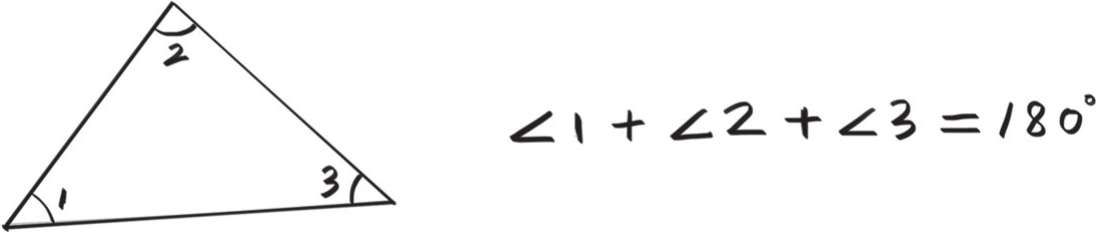
最后，推演出的结论越来越多，渐渐就形成了几何学大厦。

总结一下，公理化方法就是：在一定的定义和规则下，通过逻辑演绎整出一套东西。

这事儿就好比，程序员们只要根据一些初始代码，就能敲出一个个程序。

这套方法，后来也成了建立知识体系的典范，牛顿的力学三大定律、爱因斯坦的相对论，都是用这方法推出来的。

欧几里得也因此被称为几何之父。

到了19世纪，人们发现，这种被大家普遍认可的定义、公设，也未必是绝对真理，并由此诞生了非欧几何，但这是后话了。

二、阿基米德

作为欧几里得的徒孙，小基不仅继承了数学基因，在物理学领域也是闪闪发光，被称为力学奠基人。

他最为人熟知的，就是这三件事：

1. 泡过一个著名的澡

话说国王做了一顶金王冠，怀疑工匠掺假，让阿基米德当打假大臣，结果小基不好好干活儿，忙里偷闲洗了个痛快澡……

让初中生们苦不堪言的浮力定理，就是这么来的。

1. 打过一场不明不白的仗

这一战中阿基米德搞出了很多武器，被罗马将军称为“罗马舰队与阿基米德一人的战争”。

1. 吹过一个惊天牛皮

没错，这就是著名的杠杆原理。

总而言之，阿基米德用实际行动告诉我们：

阿基米德这种把理论和实验研究结合起来的精神，正是现代科学的精神。

已经很牛了，有没有!

但这还不是最牛的，阿基米德在数学方面也取得了巨大成就，他计算出了圆周率π≈3.14。

首先，我们要搞清楚啥叫圆周率。

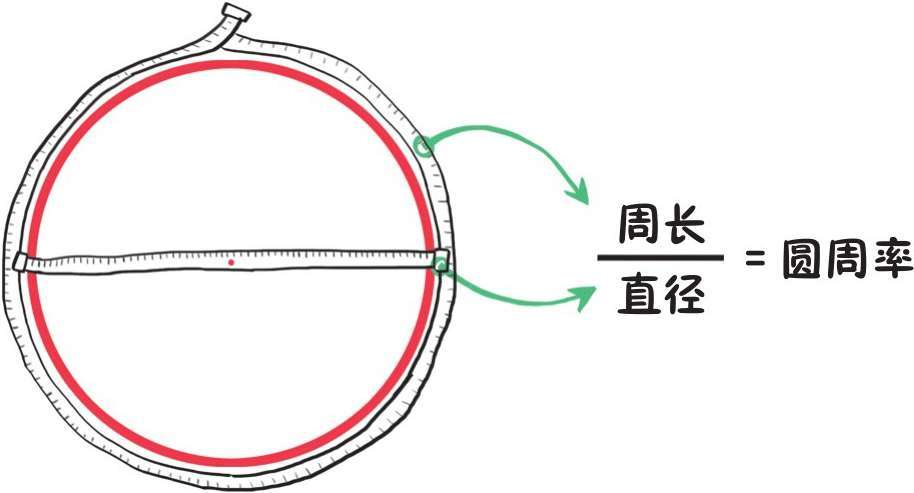
那他咋算的呢？

这里要科普一下两个概念：内接和外切。

用内接得到一个小的多边形，这个多边形的周长就比圆小。

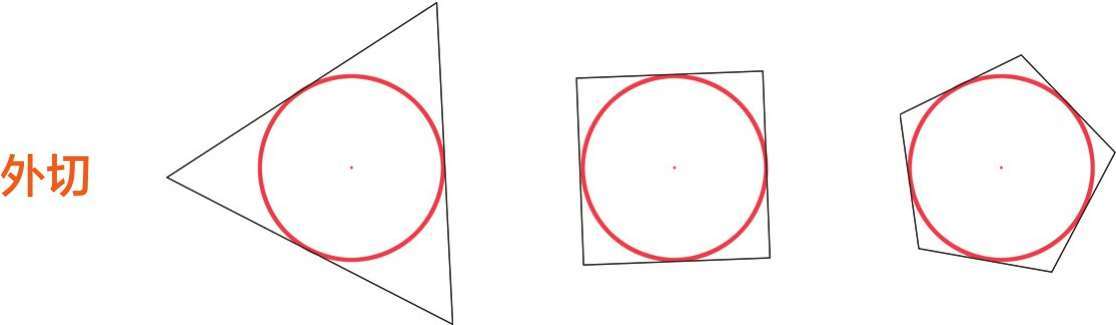
用外切得到一个大的多边形，这个多边形的周长就比圆大。

把一大一小两个圆的周长，分别除以圆的直径，就可以得到一个圆周率的取值范围。

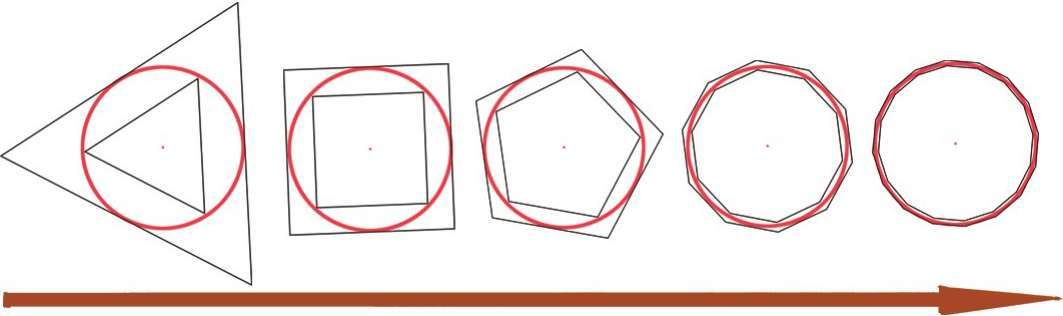
多边形的边数越多，这个取值范围就越小。

这种方法叫作穷竭法，是近代极限概念的前身。

可惜的是，公元476年，随着西罗马帝国的覆灭，西欧进入了黑暗的中世纪，持续了一千多年。黑暗的岁月里，科学该何去何从呢？

好了，关于古希腊的大神们，我们就说到这里。

我们下篇再聊!