第21章

数字类题目分析

21.1　数字规律类题目

数字规律题是笔试中一直保有的固定题型。如果给予足够的时间，数字推理并不难；但由于整体上题量大、时间短，很少有人能在规定的考试时间内做完，解答这类题目要看准趋势：首先，从整体上看数列的走向是上升还是下降，通过某个或某组数字的变化，找到问题的突破口；其次，还要熟悉题目的常见规律。数字规律题目一般包含以下10种情况：

（1）等差关系类；

（2）等比关系类；

（3）前项求和／差关系类；

（4）前项求积／商关系类；

（5）隔项规律类；

（6）分组规律类；

（7）平方规律类；

（8）质数规律；

（9）整数+小数类；

（10）组合类。

下面的例题针对以上10种情况加以解析。

面试题1：23，28，32，35，？问号里面应该是__。［德国某著名硬件公司X 2012年11月面试题］

A．37

B．32

C．38

D．35

解析：本题规律是一个典型的等差关系类，规律如下：

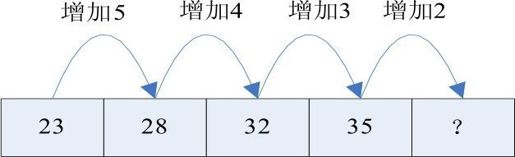
在本题中，数列差呈现5、4、3、2的递减规律。

答案：A

面试题2：24，44，68，96，128，？问号里面应该是__。［德国某著名硬件公司X 2012年11月面试题］

A．148

B．156

C．164

D．174

解析：本题规律是等差关系类的一个变形。问号处应为164，规律如下：

44-24=20=4×5；68-44=24=4×6；96-68=28=4×7；128-96=32=4×8；164-128=36=4×9

在本题中，数列差呈现4乘以5、6、7、8、9的递增规律。

答案：C

面试题3：9，16，37，?，289问号里面应该是__。［德国某著名硬件公司X 2012年11月面试题］

A．30

B．216

C．46

D．100

解析：本题规律是一个等比关系类的一个变形。问号处应为100，规律如下：

16-9=7=7×1=7×3⁰；37-16=21=7×3=7×3¹

100-37=63=7×9=7×3²；289-100=189=7×27=7×3³

在本题中，数列差为7、21、63、189，为一个等比队列（比值为3）。

答案：D

面试题4：0，1，1，2，4，7，13，？问号里面应该是__。［德国某著名硬件公司X 2012年11月面试题］

A．22

B．23

C．24

D．25

解析：本题规律是一个典型的前项求和关系类（某项的值等于前项值之和），规律如下：

0+1+1=2；1+1+2=4；1+2+4=7；2+4+7=13；4+7+13=24

在本题中，问号处应为前3项之和。

答案：C

面试题5：3，4，6，12，36，？问号里面应该是__。［德国某著名硬件公司X 2012年11月面试题］

A．372

B．216

C．156

D．212

解析：本题规律是一个前项求积关系类的变形，规律如下：

3×4÷2=6；4×6÷2=12；6×12÷2=36；12×36÷2=216

在本题中，问号处应为前2项之积再除以2。

答案：B

面试题6：34，36，35，35，36，34，37，？问号里面应该是__。［英国著名银行Z 2009年5月面试题］

A．32

B．33

C．34

D．35

解析：本题规律是一个隔项规律类。规律如下：

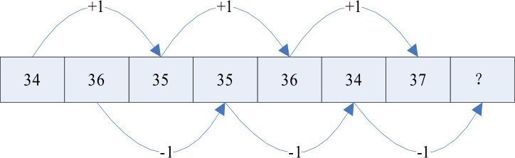
答案：B

面试题7：65，35，17，3，？问号里面应该是__。［英国著名银行Z 2009年5月面试题］

A．0

B．1

C．2

D．4

解析：本题规律是一个平方规律类。当我们看到65，35，17这样类型的数字时，我们要联想起64，36，16这样类似的数字来。64是8的平方，36是6的平方，16是4的平方。而65，35，17，3分别是：

65=8²+1；35=6²-1；17=4²+1；3=2²-1；1=0²+1

所以问号处该为1。

答案：B

面试题8：6，10，14，22，？问号里面应该是__。［英国著名银行Z 2009年5月面试题］

A．26

B．28

C．30

D．32

解析：本题规律是一个质数规律类。只有1和它本身这两个因数的自然数叫做质数。如2，3，5，7，11，13，…而6，10，14，22分别是：

6=3×2；10=5×2；14=7×2；22=11×2；26=13×2

所以问号处该为26。

答案：A

面试题9：1.01，3.02，9.03，27.05，81.08，？问号里面应该是__。［中国著名投资银行ZJ 2009年5月面试题］

解析：本题规律是一个整数+小数类。这种情况一般需要把整数和小数分开考虑。对于本题，整数部分是等比队列（比值为3），小数部分是前项求和队列：

0．01+0.02=0.03；0.02+0.03=0.05；0.03+0.05=0.08；0.05+0.08=0.13

所以问号处应为243.13。

答案：243.13

面试题10：0，6，24，60，120，？问号里面应该是__。［中国著名投资银行ZJ 2009年5月面试题］

A．186

B．210

C．220

D．226

解析：本题规律是一个组合类。这种情况一般相当复杂，解决此类问题，必须要在熟练掌握各种简单运算关系的基础上，多做练习，对各种常见数字形成一种敏感反应。至于本题，属于等差关系与立方关系的组合：

0=1³-1；6=2³-2；24=3³-3；60=4³-4；120=5³-5；210=6³-6

答案：B

21.2　数字填充类题目

面试题1：下面图中问号处该填__。［美国著名投资银行G 2009年9月面试题］

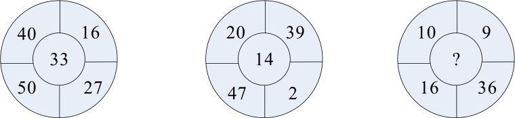
解析：数字填充类题目是近几年出现的新题型，是通过各个象限所在数字的和差积商关系求中心值。

本题规律如下：第1象限+第2象限+第4象限-第3象限=中心值

答案：9+36+10-16=39

面试题2：如下图：

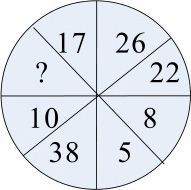
？处应该是__。［美国著名投资银行G 2009年9月面试题］

A．12

B．15

C．20

D．22

解析：注意规律，对角线之差为12，则8+12=20。

答案：C

面试题3：如下图：

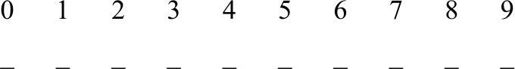
在横线上填写数字，使之符合要求。

要求如下：对应的数字下填入的数，代表上面的数在下面出现的次数，比如3下面是1，代表3要在下面出现一次。

解析：本题的情况如下：

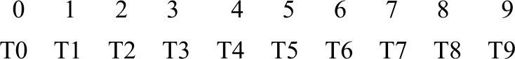
若为上面的对应关系，则

1　第2排数字之和为10。T0+T1+…+T9=10;

2　两排数字上下相乘之和也是10。0T1+1T1+…+9*T9=10。

从0入手的，0下若填9，9下面就必须是1，只剩8个位填0；0下若填8，8下面要填1，1要至少填2，只剩下7填0；……依次类推，下面填6的时候就得到答案了。

答案：6 2 1 0 0 0 1 0 0 0

21.3　数字运算类题目

关于数学运算请注意以下几点：

1．首先要明确出题者的本意不是让面试者来花费大量时间计算，题目多数情况是一种判断和验证过程，而不是用普通方法的计算和讨论过程，因此，往往都有简便的解题方法。

2．认真审题，快速准确地理解题意，并充分注意题中的一些关键信息；通过练习，总结各种信息的准确含义，并能够迅速反应，不用进行二次思维。

3．努力寻找解题捷径。大多数计算题都有捷径可走，盲目计算可以得出答案，但时间浪费过多。直接计算不是出题者的本意。平时训练一定要找到最佳办法。考试时，根据时间情况，个别题可以考虑使用一般方法进行计算。但平时一定要找到最佳方法。

4．通过训练和细心总结，尽量掌握一些数学运算的技巧、方法和规则，熟悉常用的基本数学知识；学会用排除法来提高命中率。

数学运算主要包括以下几类题型：

1．尾数排除法；2．分解计算法；3．凑整法；4．基准数法。

下面的例题针对以上4种情况加以解析。

面试题1：425+683+544+828的值是__。

A．2488

B．2486

C．2484

D．2480

解析：如果几个数的数值较大，又似乎没有什么规律可循，可以先考察几个答案项尾数是否都是唯一的，如果是，那么可以先利用个位数进行运算得到尾数，再从中找出唯一的对应项。如上题，各项的个位数相加=5+3+4+8=20，尾数为0，所以很快可以选出正确答案为D。

答案：D

面试题2：2012！末尾有几个0？

解析：乘积会产生0的，就是2的倍数与5的倍数相乘产生的。

2012/5=402；402/5=80；80/5=16；16/5=3。所以5的因子共有：402+80+16+3=501，末尾0的个数是：501个。

答案：501

面试题3：125×437×32×25=（　　）。

A．43700000

B．87400000

C．87455000

D．43755000

解析：本题不需要直接计算，只须分解一下即可：

125×437×32×25=125×32×25×437=125×8×4×25×437=1000×100×437=43700000

答案：A

面试题4：36542×42312=(？)

A．1309623104

B．1409623104

C．1809623104

D．没有正确答案

解析：解题思路是以两个乘积因子头两位数相乘(36×42)，其积应为1512，各选项中头两位数没有“15”的，所以，就没有正确答案。

答案：D

21.4　应用数学类题目

应用数学类题目包括如下几类：1.比例问题，2.路程问题，3.工程问题，4.植树问题，5.解方程问题，6.排列组合问题，7.利润问题，8.概率问题。

面试题1：Find the sum of all the three-digit numbers divisible by 7__. ［英国著名银行B 2009年10月面试题］

A．10 048

B．70 336

C．10 153

D．71 071

解析：题目是说三位数中能被7整除的数之和是多少？实际是个比例问题。

实际上考的是等差数列之和。三位数中最小能被7整除的数是105，最大能被7整除的数是994。

根据等差数列公式：

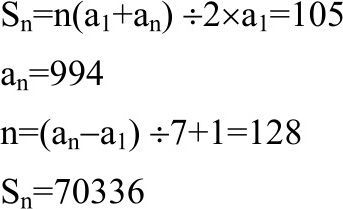
答案：B

面试题2：从A地到B地，甲电车需10小时，乙电车需要15小时，但如果两车同时行进，则甲电车速度要降下1/3，乙电车速度要降下1/10。现在两车分别处于A、B两地，要在8小时后相遇且两车同时行进的时间要尽可能少，那么甲出发__小时后，乙车就必须出发。［美国著名保险公司Y 2009年12月面试题］

A．0.5小时

B．1小时

C．1.5小时

D．2小时

解析：这是路程问题。设A B两地总路程为1，那么甲每小时行进速度为1/10，乙为1/15，

设甲行驶x小时后，乙开始行进，那么可列方程为：

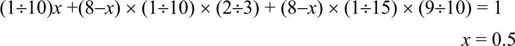
答案：A

面试题3：A battalion of 1100 people has provision for 8 weeks at 2.25kg per day per man. How many men must leave, so that the same provisions last 12 weeks at 1.65 kg per day per man__.［英国著名银行B 2009年10月面试题］

A．50

B．100

C．150

D．200

题目：一营士兵共1100人，如果要进行8周的供给，是每人每天2.25千克资源。如果供给量不变但要延长为12周，每人每天1.65千克资源，至少要裁减多少人？

解析：这是工程问题。总资源量为8×7×2.25×1100=138600（千克）。138600÷12÷7÷1.65=1000（人）。最多够1000人每人每天1.65千克资源，12周的供给量。1100-1000=100（人）。因此要裁减100人。

答案：B

面试题4：黄波一次考试成绩在班里顺数排名15，倒数也是第15名。那么黄波班里一共有学生。［中国著名投资银行ZJ 2009年5月面试题］

A．31

B．29

C．30

D．32

解析：这是植树问题，顺数排名15意味着14个人在黄波前面。倒数排名15意味着14个人在黄波后面，所以班里学生一共14+1+14=29（人）。

答案：B

面试题5：Five years' ago. Mrs. Shy was 5 times older than her daughter. Today she is 3 times as old as her daughter. How old Mrs Shy will be 5 years from now__. ［英国著名银行B 2009年10月面试题］

A．35

B．40

C．45

D．50

题目：5年前Shy的年龄是她女儿年龄5倍，现在她是她女儿年龄3倍。请问5年后Shy多少岁？

解析：这是方程问题，设Shy的年龄为X，女儿年龄为Y。根据题意列方程组：

X=3Y

X-5=5(Y-5)

解得X=30，Y=10

所以5年后也就是X+5=35

答案：A

面试题6：林辉在自助餐店就餐，他准备挑选3种肉类中的1种肉类，4种蔬菜中的2种不同蔬菜，以及4种点心中的1种点心。若不考虑食物的挑选次序，则他可以有__种不同选择方法。［中国著名证券公司G 2009年3月面试题］

A．4

B．24

C．72

D．144

解析：本题考的是组合

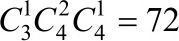
答案：C

面试题7：某个体商贩在一次买卖中，同时卖出两件上衣，每件都以135元出售，若按成本计算，其中一件赢利25％，另一件亏损25％，则它在这次买卖中是__。［中国著名证券公司G 2009年3月面试题］

A．不赚不赔

B．赚9元

C．赔18元

D．赚18元

解析：利润问题，先求成本：

135÷(1+0.25)=108（元）；135÷(1-0.25)=180（元）；180+108=288（元）

再求一共卖了多少钱：

135+135=270（元）

成本是288元，但只卖了270元，所以是赔了18元（288-270）。

答案：C

面试题8：甲乙2人相约12点至13点见面，并约定“第1人到达后可以等第2人15分钟，15分钟后第2人若不来，第1人可离去。”假设他们都以各自设想的时间来到见面地点，则他们2人能见上面的几率是__。［中国著名股份制商业银行ZS 2009年9月面试题］

A．1/16

B．1/4

C．3/8

D．以上都不对

解析：我们可以将概率问题转换为计算图形面积问题。x，y坐标表示甲乙2人等待的时间时刻。我们把一个单位看做15分钟。

设想一下，如果甲乙都在0～15分钟抵达，显然他们可以相遇。如果甲在第5分钟到达，那么乙在第20分钟到达两者也可相遇。第20分钟后则不能相遇。同理适用于乙先到的情况。如下图所示：

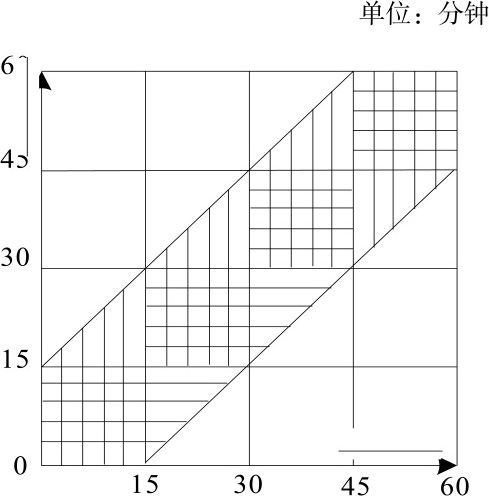
那么整个面积就是4×4=16个单位。其中相交的部分就是中间斜着的部分，面积为7。

答案：D

面试题9：64个小球放到18个盒子里，问如果要想满足以下两种情况：

1．每个盒子里面最多放6个，最少放1个；

2．18个盒子中小球数量相等这种情况的盒子越少越好。

那么18个盒子中，最多__个盒子里的小球数目相等。［美国著名保险公司Y 2009年12月面试题］

A．2

B．3

C．4

D．5

解析：概率问题，每个盒子最多放6个。那么这6个盒子里面的数量可以是1～6个。18个盒子里小球的数量从1个放到6个。然后再从第一个盒子放到第六个盒子。这样18个盒子一共能容纳63个小球。余下的1个球不管放到哪个盒子里面都可以出现4个盒子中有相同数目的球。

答案：C

面试题10：100个灯泡排成一排，第1轮将所有灯泡打开；第2轮每隔1个灯泡反转1个，即排在偶数的灯泡被关掉；第3轮每隔2个灯泡反转一次，将开着的灯泡关掉，关掉的灯泡打开。依次类推，第100轮结束的时候，还有几盏灯泡亮着。［中国著名互联网公司B 2012年12月面试题］

解析：本题显然不是期待面试者用循环套循环的傻办法来解答，找一下规律，不妨用10个灯先做一下模拟（1为亮0为灭），如下：

规律如下：当灯号的约数为奇数（即完全平方数1，4，9…）时，灯亮；反之，灯灭。所以现在问题转化为寻找100以内完全平方数个数的问题了。代码如下：

答案：10

面试题11：1001个员工羽毛球比赛，单打单淘汰制，求比几场能比出冠军？

答案：1001个员工，要淘汰1000人才能出现冠军。单淘汰制代表每次淘汰1个，所以要比1000场才能比出冠军。

面试题12：双败淘汰赛和淘汰赛相仿，也是负者出局，但负一场后并未被淘汰，只是跌入负者组，在负者组再负者（即总共已负两场）才被淘汰。现在有10个人参加双败淘汰赛，假设我们取消最后的胜者组冠军VS负者组冠军的比赛，那么一共需要举行多少场比赛？

答案：10个人5场比赛就分为负者组5人和胜者组5人，胜者组5人需进行4场即可确定胜者组冠军，负者组9个人需进行8场可确定负者组冠军，这样总共要举行17场比赛。

面试题13：对于方程x1+x2+x3+x4=30，有多少满足x1≥2,x2≥0,x3≥-5,x4≥8的整数解？

答案：稍加调整改写原方程如下：(x1-1)+(x2+1)+(x3+6)+(x4-7)=29。相当于29个1分成4组（28个空挑3个），有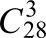=282726/(123)=3276组解。

面试题14：在区间［-2, 2］里任取两个实数，它们的和>1的概率是：

A．3/8

B．3/16

C．9/32

D．9/64

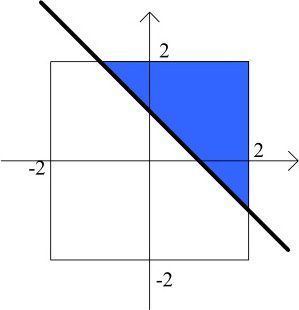
解析：概率问题。斜线以上部分的面积为>1的概率

答案：C

面试题15：小组赛，每个小组有5支队伍，互相之间打单循环赛，胜一场3分，平一场1分，输一场不得分，小组前3名出线，平分抽签。问一个队最少拿几分就有理论上的出线希望。

答案：（1）假设这个队只得1分并出线，说明它平1输3；肯定有3支队伍赢了（>3分必出线），假设不成立。

（2）假设这个队只得2分并出线，说明它平2输2；肯定有2支队伍赢了（>3分必出线），剩下的2支球队如果也是2分，仍然有通过抽签出线的可能（如10，10，2，2，2）。

面试题16：从6双不同颜色的鞋中任取4只，其中恰好有一双同色的取法有__种。

答案：C(6,1)代表从6双不同颜色的鞋中任取一双同色的的方法数。

剩余10只中任取2只是C(10,2)，在这个过程中会出现这2只是一双同色的情况C(5,1)种。所以减去后就确保了这2只不会出现是一双同色的情况。

C(6,1)*(C(10,2)-5)=240种。