第23章

智力类题目分析

23.1　推理类题目

面试题1：屋里4盏灯，屋外4个开关，一个开关仅控制一盏灯，屋外看不到屋里。怎样只进屋一次，就知道哪个开关控制哪盏灯？［中国著名国营综合性银行ZX 2009年1月面试题］

答案　四个开关ABCD。开A和B，过5分钟，关上A，B保持开着，然后开C，进去。又亮又热的，是已经开了一会儿的B，又亮又不热的是刚开的C，又不亮又热的是刚关了的A，又不亮又不热的是没有动过的D。

面试题2：一所监狱，关着N个人。每人都被关在单独的房间里，房门外面标着从1开始的号码，表示犯人的号码。突然有一天，国家发生了战争。监狱长想我是应该释放这些犯人呢？还是应该放弃他们离开这里呢？如果是一群无知的犯人，释放他们反而会给居民们带来更大的危险。如果是一群有脑子的犯人，说不定还能对抗敌人，为国家做点贡献。最后，监狱长决定用一个智力题考验监狱里的所有犯人。

问：给每个犯人的房间门外侧涂上颜色，颜色要么是“白色”，要么是“黑色”。从1号犯人开始，一次只能一个人，出来看一下其他犯人的门是什么颜色。但是看不见自己的门，因为自己的门当时是翻开的，背面靠墙了。然后犯人要猜测自己的门是什么颜色的，并告诉监狱长，然后再回到自己的房间。监狱长把每个人的答案记下来，并且统计有多少人猜对了。

如果有一半的人猜对了，就把监狱里的所有人全部释放。如果猜对的人不到一半，监狱长就放弃这些犯人，让他们饿死。

1号犯人是被关的时间最长的犯人，也是这个监狱犯人里的带头大哥。监狱长给1号犯人一个机会，让他出门后看完其他犯人的门后，可以使用监狱广播1分钟，把他的“逃命方案”告诉所有犯人，然后再回房间。

假设你是这个1号犯人，你会如何设计你的“逃命方案”呢？［中国著名投资银行ZJ 2009年12月面试题］

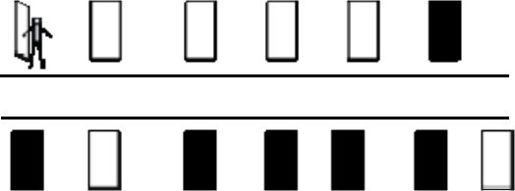
答案　设黑色门为X，白色门为Y，则总数为X+Y。1号犯人出来之后，他只会遇到三种状况。

X为1号犯人所见的数量为多数的颜色门数，Y为另一颜色门数，下式中左侧1表示1号犯人自己的门数，X+Y+1=总数。

||X-Y|-1|≥2此状况最简单，开门犯人自己的门颜色不影响大局，可直接要求所有犯人猜自己的门是处于多数的颜色（X>Y即猜X，Y>X即猜Y），即可保证半数以上的人猜对，然后过关。

||X-Y|-1|=1此状况比较复杂，此时可能是X=Y，也可能是X=Y+2，但若1号犯人要求其他所有犯人猜自己的门是处于多数的颜色（X>Y即猜X，Y>X即猜Y），同时猜自己的门为处于少数的颜色，可以保证［(X+Y)÷2+1］的犯人猜对，然后过关。

（假若X=Y，即1号犯人的门属于其所见多数门的反色，猜对，同时X个犯人猜对，结果X+1猜对，X=Y，即多于总数半数；假若X=Y+2，即1号犯人的门属于其所见多数门的颜色，猜错，同时另外X个犯人猜对，Y个犯人猜错，即对了X个，错Y+1个，但是X=Y+2，即X>Y+1，多于总数半数）。

||X-Y|-1|=0这种情况，此时可能是是X=Y+1，也可能是X=Y-1，但是很明显1号犯人的房门颜色是处于多数的那一方，因此可以要求其他犯人假如发现除自己外，所有房门颜色相加黑白数目相等的话，就猜自己的房门颜色为1号房门的颜色，而若发现所有房门颜色相加黑白数目不等，就猜自己房门为少数数目颜色，这样可以保证(X+1)÷2X的正确率，然后过关。

面试题3：1000瓶药水，其中至多有1瓶剧毒，现在给你10只狗在24小时内通过狗试药的方式找出哪瓶药有毒或者全部无毒（狗服完药X小时后才会毒发，19<X<23）。［中国著名软件咨询公司X2009年12月面试题］

答案：按十进制方式给狗编号分别是1～10。按二进制方式给药水编号。按照药水第几位数字为1，给相应的狗服药。如下：

最后看哪只狗毒发，则通过狗的编号得出药瓶号码。比如1、2、3、7、8、9号狗毒发，则第455瓶（编号0111000111）为毒药。

23.2　博弈论

面试题1：史密斯先生的遗产2000元，要分给他的2个孩子。遗嘱规定如下：

（1）由哥哥先提出分钱的方式，如果弟弟同意，那就这么分；

（2）如果弟弟不同意，1000元会捐给地震灾区，由弟弟提出剩下1000元的分钱方式；

（3）如果哥哥同意弟弟的方式，就分掉这剩下的1000元；

（4）如果哥哥不同意，遗嘱规定剩下的1000元中的800元捐给灾区，然后分别只给他们每人100元。

问：哥哥会提出什么样的分钱方式使其利益最大化？（分配最小单位元）

附带条件：两人都极聪明且唯利是图。［中国著名投资银行ZJ 2009年12月面试题］

A．1900　100

B．1899　101

C．1000　1000

D．1101　899

解析：这是一道风险评估题，属于博弈论的范畴：

如果两次都没有通过，那么两人最少获得100元，所以100元是无风险的。

第二次弟弟分配，只要给哥哥101元，弟弟获得899元。因为100元是无风险的，若少于或等于100元，哥哥“完全可以”不同意，然后获得100元。

若给哥哥的大于100元，给得越多，哥哥不同意的可能性越小。所以第二次分配的时候，弟弟可能获得的最大利益是899元，不可能再多，但是可能会更少。

回头再考虑哥哥第一次分配的情况，最低风险同样是100，给弟弟的越多弟弟同意的可能性越大。因为弟弟在第二次分配的时候可能最大获利899元，所以只要这个数目越小弟弟不同意的可能就会越大，因为可以冒险获得更大的利益。

但是只要等于899元，弟弟就没必要冒险，因为不可能获得比899元更多，况且哥哥也有不同意的可能。

所以哥哥分配的方案应该是：

哥哥：1101元。

弟弟：899元。

答案：D

扩展知识

就这道面试题来说，我们只是就题论题，考虑是两人都极其聪明理智且唯利是图。但是如果真的在实际生活中出现了这样的博弈，考虑的东西就会更多些，因为有人的地方就有变数，人的情感，性格不是机械的数字所能左右的。这些变数都会影响到实际博弈的结果。

比如说现实生活中某些人总希望别人得到的比自己少，而不管自己得到多少。于是哥哥提出1899和101的方案，如果弟弟不同意，那么弟弟提出的方案哥哥也不同意。那最后双方都得到100。对于两个人来说都是双亏的抉择，当然这是一种极端的情况。

所以我们现实考虑问题的时候，要考虑最通常的情况：即每个人都希望拿得尽量多，如果万一拿得比对方少，也不要差距太大（古人云不患寡患不均）；所以实际生活中的情况可能是这样的：

1．假如进入第二轮分配，弟弟会冒险地提出899、101的分配方案吗？显然不会，这个风险太大了，他完全没有胜算。因为哥哥可能宁可不要多的一块钱，也要和弟弟差距不大。他必须拿出一定的钱来换取哥哥至少有50％以上的可能性来同意他的分配方案，只要在保证分配方案得到对方点头的情况下，利益最大才能得到体现，因此要博弈就不该仅仅考虑自己的利益，这放在商业上也是这样的；

2．弟弟的方案，最保险的是每人500，但既然要考虑利益最大，那就不可能是公平地进行分配，那弟弟的分配方案应该是让哥哥得到100到500的中间值，也就是300，自己得到700；

3．那么，如果哥哥考虑到弟弟可能提出的这种方案的话，也就是让弟弟得到700，自己得到1300。这种分配方案，弟弟同意的可能性过半，所谓博弈就在于此，不能一味去追求极端。

这道题出得非常好，它告诉了我们好伙伴之间怎样合理分配利益，这是两者能长久合作的基础之一。大家都是做企业的，获取最大利润无可争议；既然我们是兄弟般的合作者，分配的方法应该让双方心服口服；不要以为只有自己是智者，也不要压人，总之要有理有节达到共赢的局面。

面试题2：有一栋10层的楼，在每个电梯门口放上一颗钻石，这些钻石的大小不同，一人坐电梯从1楼到10楼，电梯每到一层楼都开一次门，请问怎么样能拿到最大的钻石。只有一次机会（就是出了电梯门就进不来了）。［中国著名综合保险公司RB 2009年1月面试题］

解析：本题考的是管理学中最优决策与满意决策的问题。

采用最优决策，决策者必须在给定约束条件下选出一个能产生最优秀后果（如利润最大、成本最小或其他目标最好）的行动方案，以求一次性地从根本上解决问题。但最优化是一种理想化的追求，在现实中只有为数很少的情况下才能用得上这种决策准则，而在大多数情况下，通常只能采取满意化决策准则，即只要求将既定目标实现到足够好、令人满意就行了。

答案：前3个不管多大都不拿，从第四个开始，如果比前面的钻石大或与前面最大类型相似的就拿，否则就不拿。如果到10楼还没选择好，就拿10楼的。

T公司这道题目借鉴的是一个有关苏格拉底弟子摘麦穗的问题：

古希腊哲学大师苏格拉底的三个弟子求教老师：怎样才能成功呢？苏格拉底没有直接回答，让他们去走麦田埂，只许前进，且仅给一次机会，要求是：选摘一个最好最大的麦穗。第一个弟子没走几步就看见一个又大又漂亮的麦穗，高兴地摘下来。但他继续前进时，发现前面有许多麦穗比他摘的那个大，但他没有机会了，只得遗憾地走完全程。第二个弟子正好相反，每当要摘时，总是自我提醒，后面可能还有更好的。他一直走到终点才发现自己失去了很多机会。第三个弟子的做法是当他走过全程的1/3时，即分为大、中、小三类；再走过1/3时，验证分类是否准确；在剩下的1/3里，他较早地选择了位于大麦中的一个美丽的麦穗。虽然这个麦穗不一定是麦田里最大的，但肯定还是不错的。

23.3　概率

面试题1：一个鱼塘，养鱼若干，请想一个办法尽量准确的估算其中有多少条鱼？［中国著名基金管理公司N 2009年12月面试题］

解析：本题考的是概率论中的放回抽样。

以从一个口袋中取球为例，每次随机地取一只，每次取一只球后放回袋中，搅匀后再取一球，这种取球方式为放回取样。每次取一只球后不放回袋中，下一次从剩余的球中再取一球，这种取球方式为不放回取样。

答案：先从塘里捞个100条鱼（可以根据鱼塘里鱼的大概数量级适当变化）然后为每条鱼做一个标记（例如绑上一条丝带），再放回去。一天以后，再捞上100条，数一数有多少是做了标记的。可以假设这时做了标记的鱼是均匀分布在鱼塘里的，所以大概就能估计出一共有多少条鱼了。

比如说发现20条鱼有标记，那么总鱼数大概为500条（100×100÷20）。

面试题2：概率问题

（1）一个普通的骰子，连抛2次都是1点，问：抛第3次是1点的概率是小于1/6，大于1/6，还是等于1/6？

（2）一个普通的骰子，连抛10次都是1点，问：抛第11次是1点的概率是小于1/6，大于1/6，还是等于1/6?［上海著名证券公司S 2009年8月面试题］

解析：在概率论中，有一个概念叫独立事件。事件A（或B）是否发生对事件B（或A）发生的概率没有影响，则称A与B是相互独立事件。贝努里（瑞士数学家和物理学家）有一个独立重复试验：同样的条件下重复地、各次之间相互独立地进行的一种试验。贝努里试验有个结论，n次独立重复试验里，某事件A恰好发生k(k=0, 1, …, n)次的概率P_n(k)，组成离散型随机变量的二项分布：

P_n(k)=C (n, k) p^k (1-p)^n-k

掷骰子符合独立事件。投掷1次为1点的概率p=1/6，不是1点的概率为5/6。

如果本问题换一种问法：

（1）一个普通的骰子，连抛3次都是1点的概率是？（此时n=k=3，p=1÷6，P_n(k)=1÷6³）

（2）一个普通的骰子，连抛11次都是1点的概率是？（此时n=k=11，p=1÷6，P_n(k)=1÷6¹¹）

对比本题：

（1）一个普通的骰子，连抛2次都是1点，问：抛第3次是1点的概率是小于1/6，大于1/6，还是等于1/6？

（2）一个普通的骰子，连抛10次都是1点，问：抛第11次是1点的概率是小于1/6，大于1/6，还是等于1/6？

这问法不一样了，对于第1题，它假设了前2次都出现了1点，但第3次仍为独立事件，与前2次无关。第3次出现的概率仍然为1/6。第2题也一样是1/6。

从概率论来说，全是等于1/6。因为事件都是独立的。但从人的感觉来说，既然出了10次1点，再出1点的可能性较小。这种错误的感觉迷惑很多人。我们往往会被实际经验左右自己的结论，但我们要坚信理论！有人会问：本题中，连抛10次都是1点这种事情太怪了，简直不可能！概率论里，不可能事件的发生概率是0，但0概率事件可能发生。比如在宇宙中抽一个人，抽到你的概率。这就是一个0概率事件可能发生的例子！

随机变量分连续和离散两种，它们各自的分布描述是不同的。对于连续性随机变量，单个具体点的概率密度值为一有界常数，这个值可以是任意的（包括0和1），但因为点是没有长度的，所以该点的概率密度积分为0（因为该点概率密度值有界），即该点所对应的事件发生的概率为0，但这个事件仍然是可能发生的，因为这个事件在事件域内。也就是说，概率为0的事件有可能发生。同理，某个点的概率密度值为1，但该点的概率密度积分仍为0，所以概率为1的事件也不一定必然发生。总之，对于连续性随机变量，讨论单个点的概率是没有意义的（都为0），我们讨论的是这个随机变量落在一个区间内的概率。

对于离散随机变量，如果它的事件域是有限个事件，则可以认为概率为0的事件一定不会发生，概率为1的事件必然发生。但若事件是无限的，则还要具体分析，既然0概率事件都是有可能发生的，那么概率趋近于零的事件果然有可能发生，只不过我们平时在处理问题的时候，把概率接近零的事件算作0概率事件，只是算作，不是绝对。

本题有三个前提：

（1）既然题目说是“一个普通的骰子”，按照常理就是有6种数字的骰子；

（2）普通骰子投一次投出1的概率是1/6；

（3）概率本身就一个估计值，0概率事件都可能发生，更不要说小概率事件了。

所以最后的结论是：

投10次连续出现10次1的概率是1/6的10次方，但这个小概率事件的发生和下一次投没有关系。如果承认“普通骰子投一次出现1的概率是1/6”，那么下次出现1的概率还是1/6。

答案：1/6，1/6。