2.6　非对称密码体制

1976年，密码学专家Diffie和Hellman在《密码学的新方向》一文中提出了公开密钥密码体制的思想，开创了现代密码学的新领域，非对称密码体制的篇章由此揭开。

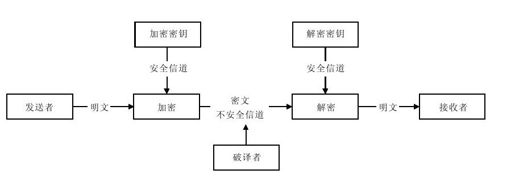
非对称密码体制的保密通信模型如图2-9所示。非对称密码体制与对称密码体制相对，其主要的区别在于：非对称密码体制的加密密钥和解密密钥不相同，分为两个密钥，一个公开，一个保密。公开的密钥称为公钥，保密的密钥称为私钥。因此，非对称密码体制也称为公钥密码体制。非对称密码体制使得发送者和接收者无密钥传输的保密通信成为可能，弥补了对称密码体制的缺陷。

图　2-9　非对称密码体制的保密通信模型

在非对称密码体制中，公钥和私钥均可用于加密与解密操作，但它与对称密码体制有极大的不同。公钥与私钥分属通信双方，一份消息的加密与解密需要公钥与私钥共同参与。公钥加密则需要私钥解密，反之，私钥加密则需要公钥解密。我们把通信双方定义为甲乙两方，甲乙两方分场景扮演信息发送者或接收者。公钥与私钥分属甲乙两方，甲方拥有私钥，乙方拥有公钥。为了更好地描述非对称密码体制通信流程，我们通过图2-10、图2-11来说明甲乙双方如何完成一次完整的会话。

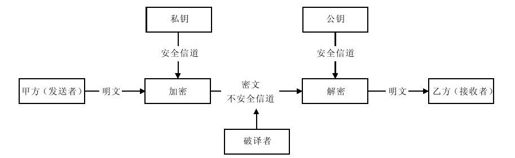
甲方（发送方）用私钥加密数据向乙方发送数据，乙方（接收方）接收到数据后使用公钥解密数据，如图2-10所示。

图　2-10　私钥加密-公钥解密的保密通信模型

乙方（发送方）用公钥加密数据向甲方发送数据，甲方（接收方）接收到数据后使用私钥解密数据，如图2-11所示。

非对称密码体制的主要优点是可以适应开放性的使用环境，密钥管理问题相对简单，可以方便、安全地实现数字签名和验证。RSA是非对称密码体制的典范，它不仅可以完成一般的数据保密操作，同时它也支持数字签名与验证。关于数字签名，请参见2.8节。除了数字签名，非对称密码体制还支持数字信封等技术。我们将在后续章节详细讲述该类技术的具体实现。

非对称密码算法的安全性完全依赖于基于计算复杂度上的难题，通常来自于数论。例如，RSA源于整数因子分解问题；DSA—数字签名算法，源于离散对数问题；ECC—椭圆曲线加密算法，源于离散对数问题。由于这些数学难题的实现多涉及底层模数乘法或指数运算，相对于分组密码需要更多的计算资源。为了弥补这一缺陷，非对称密码系统通常是复合式的：用高效率的对称密码算法对信息进行加密解密处理；用非对称密钥加密对称密码系统所使用的密钥。通过这种复合方式增进效率。

图　2-11　公钥加密-私钥解密的保密通信模型