2.7　散列函数

在讲到对称密码体制的流密码实现方式时，曾经提到过对于信息完整性验证需要其他技术来支持，这种技术就是由散列函数提供的消息认证技术。

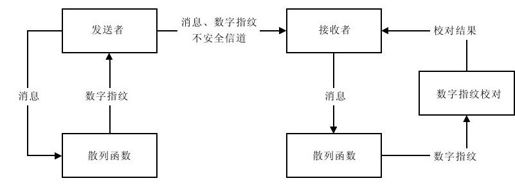
散列函数，也称做哈希函数、消息摘要函数、单向函数或杂凑函数。与上述密码体制不同的是，散列函数的主要作用不是完成数据加密与解密的工作，它是用来验证数据的完整性的重要技术。通过散列函数，可以为数据创建“数字指纹”（散列值）。散列值通常是一个短的随机字母和数字组成的字符串。消息认证流程如图2-12所示。

图　2-12　消息认证流程

在上述认证流程中，信息收发双方在通信前已经商定了具体的散列算法，并且该算法是公开的。如果消息在传递过程中被篡改，则该消息不能与已获得的数字指纹相匹配。

散列函数具有以下一些特性：

❑消息的长度不受限制。

❑对于给定的消息，其散列值的计算是很容易的。

❑如果两个散列值不相同，则这两个散列值的原始输入消息也不相同，这个特性使得散列函数具有确定性的结果。

❑散列函数的运算过程是不可逆的，这个特性称为函数的单向性。这也是单向函数命名的由来。

❑对于一个已知的消息及其散列值，要找到另一个消息使其获得相同的散列值是不可能的，这个特性称为抗弱碰撞性。这被用来防止伪造。

❑任意两个不同的消息的散列值一定不同，这个特性称为抗强碰撞性。

散列函数广泛用于信息完整性的验证，是数据签名的核心技术。散列函数的常用算法有MD—消息摘要算法、SHA—安全散列算法及MAC—消息认证码算法。我们将在后续章节详述上述散列函数的算法实现。