8.3.2　模型分析

我们继续以消息传递模型为例，阐述基于RSA算法的消息传递模型是如何工作的。

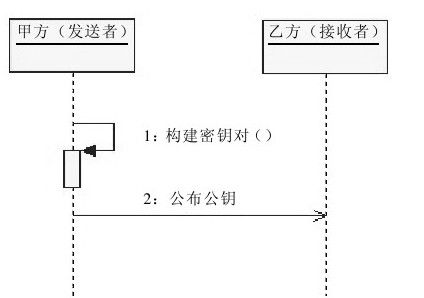
RSA算法代表了真正的非对称加密算法，其操作较之DH算法较为简单。在构建密钥对方面，RSA算法就相当简单，如图8-5所示。

在图8-5中，我们仍以甲乙两方收发消息为例。甲方作为消息的发送方，乙方作为消息的接收方。我们假设甲乙双方在消息传递之前已将RSA算法作为消息传递的加密算法。为完成加密消息传递，甲乙双方需要以下操作：

通过了解基于DH算法的消息传递模型，我们更容易理解基于非对称加密算法的消息传递模型的工作方式。或者说，基于DH算法的消息传递模型更为底层。

图　8-5　构建RSA算法密钥对

1）由消息发送的一方构建密钥对，这里由甲方完成。

2）由消息发送的一方公布公钥至消息接收方，这里由甲方将公钥公布给乙方。

完成这两步操作后，甲乙双方就可以进行加密消息传递了，如图8-6和图8-7所示。

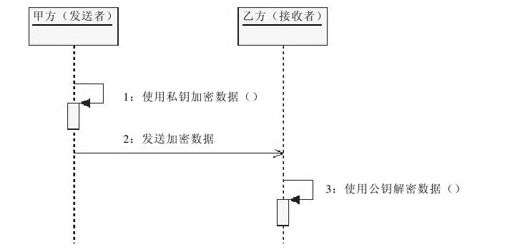
图　8-6　甲方向乙方发送RSA算法加密数据

这里需要读者朋友注意：甲方向乙方发送数据时，使用私钥对数据做加密处理；乙方接收到加密数据后，使用公钥对数据做解密处理。

我们需要注意，在非对称加密算法领域中，对于私钥加密的数据，只能使用公钥解密。简言之，“私钥加密，公钥解密”。

相对于“私钥加密，公钥解密”的实现，RSA算法提供了另一种加密/解密方式：“公钥加密，私钥解密”。这使得乙方可以使用公钥加密数据，如图8-7所示。

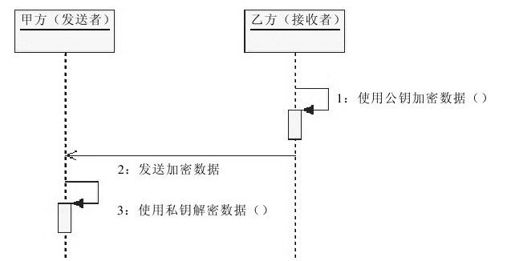
图　8-7　乙方向甲方发送RSA算法加密数据

甲方可以向乙方发送加密消息，乙方也同样可以向甲方发送加密消息。在图8-7中，乙方使用公钥加密消息，甲方则使用私钥对加密消息解密。这是一种“公钥加密，私钥解密”的加密/解密方式。

用公钥加密数据的方式是否可取呢？公钥是通过甲方发送给乙方的，其在传递过程中很有可能被截获，也就是说窃听者很有可能获得公钥。如果窃听者获得了公钥，向甲方发送数据，甲方是无法辨别消息的真伪的。因此，虽然可以使用公钥对数据加密，但这种方式还是会有存在一定的安全隐患。如果要建立更安全的加密消息传递模型，就需要甲乙两方构建两套非对称加密算法密钥，仅遵循“私钥加密，公钥解密”的方式进行加密消息传递。