6.6　循环冗余校验算法—CRC算法

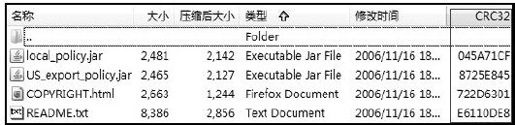
大家对于“奇偶校验码”和“循环冗余校验码”这样的名词应该不会感到陌生。即便不是计算机专业出身，也一定使用过压缩软件WinRAR，在压缩文件列表中能看到一个标有“CRC32”字样的内容，如图6-8所示。

图　6-8　压缩包中的CRC32算法

“奇偶校验码”、“循环冗余校验码”和“CRC32”都是同一套东西，它们和CRC有着紧密的联系。

CRC算法并不属于加密算法范畴，但与本章内容较为接近，故在这里为读者朋友做简要介绍。

6.6.1　简述

CRC（Cyclic Redundancy Check，循环冗余校验）是可以根据数据产生简短固定位数的一种散列函数，主要用来检测或校验数据传输/保存后出现的错误。生成的散列值在传输或储存之前计算出来并且附加到数据后面。在使用数据之前，对数据的完整性做校验。一般来说，循环冗余校验的值都是32位的二进制数，以8位十六进制字符串形式表示。它是一类重要的线性分组码，编码和解码方法简单，检错和纠错能力强，在通信领域广泛地用于实现差错控制。

由上述内容分析，消息摘要算法与CRC算法同属散列函数，并且CRC算法很可能就是消息摘要算法的前身。

CRC算法历经了多个版本的演进，从最初的CRC-1算法至最终的CRC-160算法，为消息摘要算法奠定了基础。我们简单回顾一下CRC算法的发展历程：

❑CRC-1：主要用于硬件，就是我们常说的奇偶校验码。

❑CRC-32-IEEE 802.3：主要用于通信领域实现差错控制，也就是我们今天常说的CRC-32，IEEE 802.3只是一种标准。

❑CRC-32-Adler：CRC-32的一个变种，可以称为“Adler-32”，与CRC-32一样可靠，但是速度更快。

❑CRC-128：演变为今天的MD算法。MD算法消息摘要值为128位二进制数。

❑CRC-160：演变为今天的SHA算法。SHA-1算法消息摘要值为160位二进制数。

至今，CRC-32算法仍是各种压缩算法中最为常用的数据完整性校验算法。而它的变种Adler-32普遍用于zlib压缩算法中的数据完整性校验。