面试题51：海盗分金币

问：5个海盗抢到100枚金币后，讨论如何进行公正分配。他们商定的分配原则如下。

（1）抽签确定各人的分配顺序号码1、2、3、4及5。

（2）由抽到1号签的海盗提出分配方案，然后5人进行表决，如果方案得到超过半数的人同意，就按照他的方案进行分配，否则就将抽到1号签的海盗扔进大海喂鲨鱼。

（3）如果抽到1号签的海盗被扔进大海，则由抽到2号签的海盗提出分配方案，再由剩余的4人进行表决，如果方案得到超过半数的人同意时，就按照他的方案进行分配，否则也将其扔入大海。

（4）依次类推。

这里假设每1个海盗都是绝顶聪明而理性的，他们都能够进行严密的逻辑推理，并能很理智地判断自身的得失，即能够在保住性命的前提下得到最多的金币。同时还假设每一轮表决后的结果都能顺利得到执行，那么抽到1号签的海盗应该提出怎样的分配方案才能使自己既不被扔进海里，又可以得到较多的金币呢？

答案：如表21.3所示。

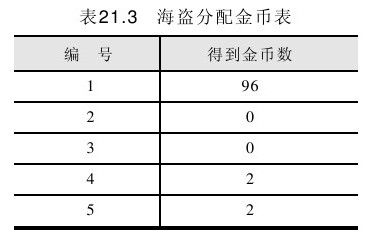
推理方法：如果当对3的方案表决时，4一定会支持3，否则的话他就要被5反对，从而死。因此，如果1，2死了，3的方案肯定是100，0，0，并且一定会得到3和4的支持，此时4，5的收入为0，因此1，2可以贿赂4，5而得到支持。同时3的期望收入为100，他必定会不顾一切地反对1，2。而如果1死了，2的方案肯定是98，0，1，1，并且一定会通过。所以1的最优方案为96，0，0，2，2，并且一定会通过。其实98，0，0，1，1也可以，并且有可能通过（看4，5的心情和残忍程度而定）。