第一部分 复杂网络的起源

第2链 随机宇宙

网络的构造和结构是理解复杂世界的关键。我们每个人都是遍及全世界的社会网络这个大节点簇的一部分，没有人能游离在外。当自然界闭着眼睛抛洒链接时，长远来看，没有节点会被青睐，也没有节点会被歧视。哪怕只影响少数几个节点或边，就能打开隐藏的大门，让新的可能涌现。沿着网络中的链接，个体的行为可以很容易地影响到数百万人。

随机网络

随机网络是指通过随机连接节点搭建起来的网络。在随机网络中，链接是完全随机放置的，所有节点有相等的机会获得链接。只要网络足够大，几乎所有节点拥有的链接数都基本相同。因此，随机网络是一个高度平等的网络。

图论

图论是数学的一个分支。它以图为研究对象。图论中的图是由若干给定的点及连接两点的线所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系，用点代表事物，用连接两点的线表示相应两个事物间具有这种关系。

欧拉的图论与哥尼斯堡七桥问题

1783年9月18日，圣彼得堡，和往常一样，莱昂哈德·欧拉（Leonhard Euler）在给他的一个孙子上了一堂数学课后，做了一些关于热气球飞行的计算。三个月前，在里昂南部，蒙戈尔费兄弟（Montgolfier brothers）发射了一个巨大的热气球，气球升到1980米的高空，在大约1.6公里外安全着陆。在欧拉探究热气球运动的力学原理时，蒙戈尔费兄弟正准备在国王路易十六面前展示他们的热气球飞行。他们计划利用热气球把一只羊送到空中，飞行将于次日在巴黎进行。然而，欧拉没能坚持到这次飞行的进行。午饭后，欧拉和他的助手一起针对新近发现的行星——天王星的运行轨道做了一些计算。欧拉提出了一组刻画天王星奇特轨道的方程，数十年后，这组方程帮助人们发现了海王星。而欧拉同样没能见证海王星的发现。大约下午5点钟，欧拉突发脑溢血，在失去意识前他说道：“我就要死了。”那天晚上，欧拉去世了，走完了数学界有史以来最高产者的一生。

欧拉是一位出生于瑞士的数学家，他的职业生涯在柏林和圣彼得堡度过，他在数学、物理学、工程学等领域都有着非凡的影响。不仅因为他的发现具有无可比拟的重要性，而且因为他的发现的数量也令人望尘莫及。欧拉的著作部分收录于《欧拉全集》（Opera Omina），这部全集目前已超过73卷，每卷600页。从1766年回到圣彼得堡直到76岁去世，欧拉生命的最后17年可谓相当动荡。尽管遭遇了很多人生悲剧，他在这段时间还是完成了一半的著作，其中包括一部776页的研究月亮运动的专著、一部具有深远影响的代数教科书和一部微积分的三卷本论集。在完成这些著作的同时，他平均每周还在圣彼得堡学院期刊上发表一篇数学论文。不可思议的是，在这段时间他基本上没有写过或者读过一行字，因为自1766年回到圣彼得堡不久，他就丧失了部分视力。1771年，白内障手术失败后，欧拉完全失明了。这期间，他完成的数千页著作都是凭记忆口述的。

三十年前，视力良好的欧拉曾写过一篇简短的论文，探讨源自哥尼斯堡（Königsberg）的一个有趣的问题。哥尼斯堡距离欧拉在圣彼得堡的家不远，这座四处开满鲜花的小镇位于东普鲁士境内。在18世纪早期，哥尼斯堡并没有预料到自己将来会遭受战争破坏——这里后来成为第二次世界大战最激烈的战场之一。正如当时的一幅蚀刻版画描绘的那样，位于普瑞格尔（Pregel）河畔的哥尼斯堡是一座欣欣向荣的城市，忙碌的船队和繁荣的贸易让当地的商人和居民过着富足的生活。经济的健康发展为市政府提供了财力保障，于是，市政府在普瑞格尔河上建造了7座桥。大多数桥将城中美丽的奈佛夫岛（Kneiphof）和城市的其他部分连接起来。奈佛夫岛位于普瑞格尔河的两条分支之间，河的这两条分支之间由两座桥相连（如图2-1所示）。生活在和平和富足之中的哥尼斯堡人喜欢玩智力游戏，其中一个智力游戏是：“人们能否不重复地走完城中的7座桥？”在1875年一座新桥落成之前，没有人找出过这样的路径。

1736年，即新桥建成前大约150年，欧拉给出了一个严格的数学证明，告诉我们：在7座桥的情况下，不重复地走完所有桥的路径是不存在的。在这篇简短的论文里，欧拉不仅解决了哥尼斯堡问题，还在不经意间开启了一个重要的数学分支——图论。今天，图论已经成为我们考察网络的基础。在欧拉去世后的几个世纪里，在大批数学家的贡献下，图论逐渐发展成熟。为了打开网络的大门，让我们先简要回顾一下欧拉画出第一张图时的推理过程。

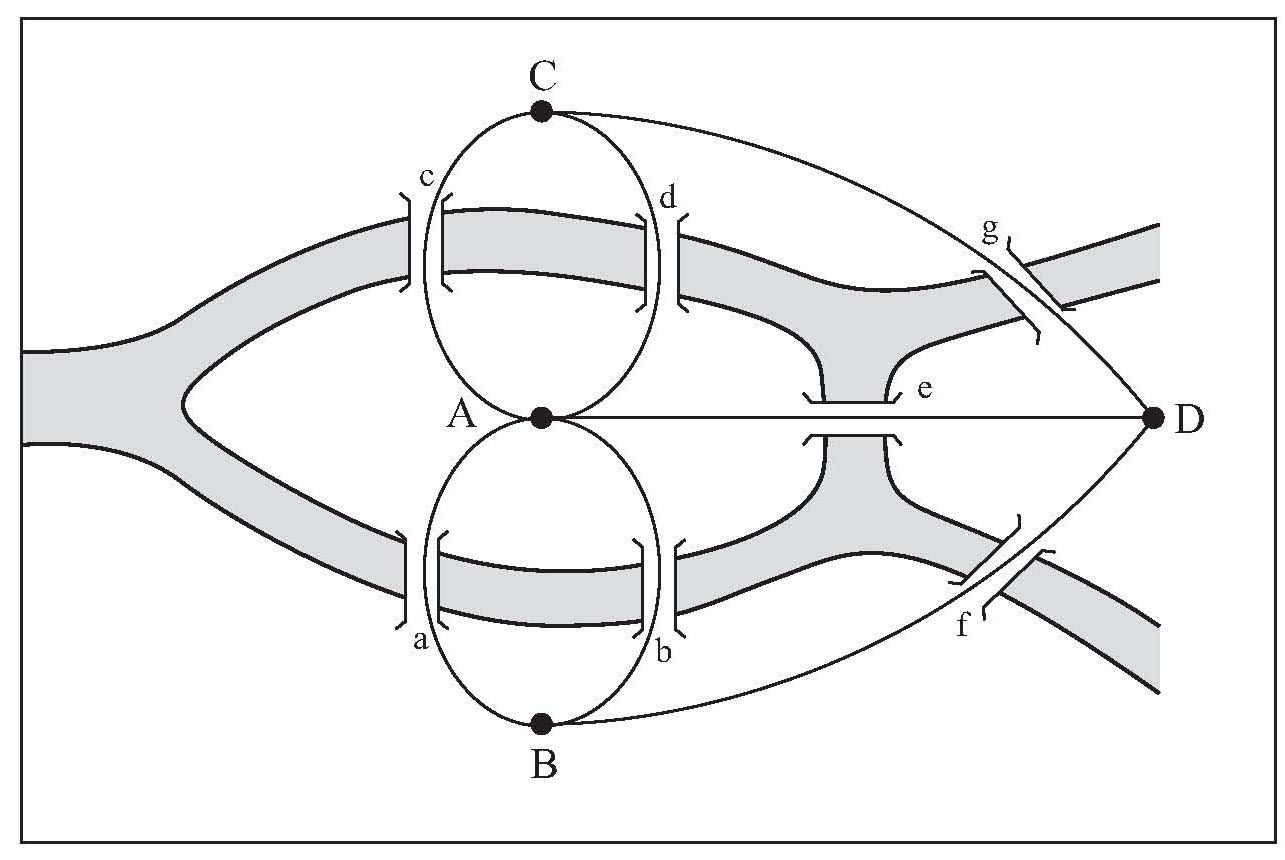
1875年之前哥尼斯堡的版图：奈佛夫岛（A）和陆地区域D处于普瑞格尔河的两条分支之间。求解哥尼斯堡问题意味着，寻找一条巡游全城的路径，每个桥只经过一次。1736年，莱昂哈德·欧拉提出了图论，将四块陆地表示成节点A到D，7座桥表示为链接a到g，于是得到了一个有四个节点和七条边的图。他随后证明，在哥尼斯堡图中，不存在一条经过每条链接仅一次的路径。

图2-1 哥尼斯堡7桥问题

网络构造，理解复杂世界的关键

欧拉的证明简洁而优美，即使是没有受过数学训练的人也能很容易地理解。然而，改变历史的不是证明本身，而是他求解问题时的一个中间步骤。欧拉最伟大的洞察力表现在他将哥尼斯堡问题视为一张图，即通过边连接在一起的一组节点。在哥尼斯堡问题中，他用节点表示被河流分开的四块陆地，分别用字母A、B、C、D来表示。然后，用一条连接两个节点的线表示连接两块陆地的每座桥，他把桥称为边。欧拉得到了一张图，节点代表陆地，边代表桥。

欧拉证明了哥尼斯堡不存在一条路径能够走遍所有7座桥而不重复，他的证明基于一个简单的观察：在网络上沿着边“旅行”时，拥有奇数条边的节点，要么是旅行的起点，要么是旅行的终点。走遍所有桥的连续路径只有一个起点和一个终点。因此，如果图中有多于两个节点拥有奇数条边，就不存在前文所述的路径。而哥尼斯堡的图中有四个这样的节点，所以人们找不出他们希望找到的路径。

对于我们而言，欧拉的证明最重要的意义在于，这样的路径是否存在不取决于我们寻找路径的能力，仅取决于图的性质。在哥尼斯堡桥梁布局给定的情况下，无论我们多么聪明，都不可能找到期望的那样一条路径。哥尼斯堡人最终认同了欧拉的结论，放弃了毫无结果的寻找，转而选择于1875年在节点B和C之间建造了一座新桥，让这两个节点各自拥有的边数增加到4。现在，只有两个节点（A和D）有奇数条边了，找到一条经过每座桥仅一次的路径变得非常容易。也许，建造这座新桥背后的原因就是为了创造这样一条路径。

链接洞察

回想起来，欧拉无意间阐述的信息其实非常简单：图或网络具有一些隐藏在自身结构背后的性质，这些性质可以限制或者增强我们在网络中所能施展的能力。两个多世纪以来，哥尼斯堡人求解他们在咖啡馆里谈论的那个问题的能力，一直受哥尼斯堡版图布局的限制。但是，在增加一条边改变布局后，这个限制就突然消失了。

欧拉的证明结果从多个方面体现了本书的一个重要观点：图或网络的构造和结构是理解我们周围复杂世界的关键。拓扑结构的微小变化，即使只影响少数几个节点或边，也能打开隐藏的大门，让新的可能涌现出来。

欧拉之后，图论领域获得了快速发展，这得益于数学大师们的贡献，包括柯西（Cauchy）、哈密顿（Hamilton）、凯利（Cayley）、基尔霍夫（Kirchhoff）和波利亚（Pólya）。他们几乎揭开了那些大而有序的图中的所有奥秘，包括晶体中原子间形成的格或蜂巢中蜜蜂建造的六角栅格。20世纪中叶之前，图论的研究目标比较简单：发掘各种类型的图的性质并对其进行分类。著名的图论问题包括：1873年首次解决的迷宫问题，以及在国际象棋棋盘上寻找一个让马遍历所有方格各一次并回到原点的步骤序列。有一些比较难的问题，几个世纪以来都无人能解。

在欧拉极富启发性的工作完成两个世纪后，数学家才开始从研究不同图的性质转到研究更深入的问题，即图或网络（更常见的称谓）是如何形成的。真实的网络是如何形成的呢？支配网络外观和结构的法则是什么呢？直到20世纪50年代两个匈牙利数学家对图论进行革新时，上述问题才被提出并得到第一个答案。

埃尔德什，网络是如何形成的

20世纪20年代后期的一个下午，一个17岁的年轻人在布达佩斯的街道上慢跑，步态怪异。他在一家卖定制鞋的高档鞋店前停下了脚步。他的脚形状奇特，普通的鞋子都无法穿着，只得找人定做鞋子。但是，他来这里并不是为了定做新鞋。他敲过门后（这一举动无论在现在还是在当时都显得有些奇怪），便走了进去，没理会柜台后的女售货员，就径直走向鞋店最里面的一个14岁男孩。

“告诉我一个四位数。”他说道。

“2532。”男孩瞪大眼睛紧盯着这位奇怪的人回答道。不过，那个年长些的男孩没有让他注视太久。

“它的平方是6411024，”他继续说道，“抱歉，我现在年龄大了，不能告诉你它的立方是多少了。你知道多少种毕达哥拉斯定理的证明方法？”

“一种。”年轻的那个男孩回答道。

“我知道37种，”他不做停顿继续说，“直线上的点组成的集合是不可数的，你知道吗？”在为这个聪明的小男孩讲解完康托尔（Cantor）的证明方法后，他在鞋匠店的任务就完成了。说了声“我得走了”，他便大步跑出了鞋店。

保罗·埃尔德什（Paul Erdös）一路飞奔，迅速成为20世纪的顶尖天才和最著名的异类。1996年去世前，他完成了1500多篇数学论文，他的高产自欧拉之后无人企及。在这些学术作品中，有8篇论文是和另一位匈牙利数学家阿尔弗雷德·莱利（Alfréd Rényi）合作发表的。这8篇论文在历史上首次探讨了理解相互关联的宇宙的最基本问题：网络是如何形成的？他们的解答为随机网络理论奠定了基础。这个优美的理论深刻地支配着我们思考网络的方式，我们至今仍难以摆脱它的影响。

只需30分钟，一个无形社会网络的形成

假设有一个聚会，应邀参加的100名宾客均互不相识。为这群陌生人提供葡萄酒和奶酪，他们很快便会聚在一起相互交谈，因为人类与生俱来的社交诉求会驱使他们这样做。他们三三两两地分成了三四十个小组。现在，向其中一位客人透漏，那瓶没有标签的深绿色瓶子中的红葡萄酒是窖藏20年的罕见佳酿，比贴有红色标签瓶子中的葡萄酒好很多，然后要求这名客人只能把这个消息和他新认识的人分享。你知道你那瓶昂贵的酒很安全，因为知道这个消息的客人可能刚刚结识两三个人。但是，客人们不会和同一个人没完没了地聊很久，他们很快会形成新的小组。在外人看来，这并没有什么特别。然而，早先结识的人之间已经建立了无形的社会链接，现在他们又分散到了不同的组里。如此一来，另一些仍互不相识的客人之间便可以通过这些微妙的路径联系起来。

例如，尽管约翰还没有碰到过玛丽，但他们都见过迈克，于是就有一条从约翰通过迈克到玛丽的路径。如果约翰知道红葡萄酒的消息，玛丽便也有可能会知道，因为她会从迈克那里听到这个消息，而迈克的消息来自约翰。

随着时间的推进，客人们逐渐由这种无形的链接联系在一起，相当一部分人之间形成了一个很好的熟识网络。随着葡萄酒的消息从最初少量的知情者扩散到越来越多的聊天组里，那瓶昂贵的葡萄酒变得越来越不安全。

如果每个人都把消息传递给他新认识的人，那么在聚会结束之前，是不是所有客人都知道那瓶好葡萄酒的存在了呢？可以肯定的是，如果所有人都互相认识，最终每个人都会到那个没有标签的瓶子中取好葡萄酒。但是，即使每次碰面只需要10分钟，和其他99个人都碰到也需要大约16个小时，而极少有聚会能持续那么久。因此，你可能会觉得，把那瓶葡萄酒的秘密告诉你的朋友也无妨，而且你有理由相信，那瓶葡萄酒在聚会结束时还会剩下一些。

但保罗·埃尔德什和阿尔弗雷德·莱利不认同上述观点。埃尔德什经常引用莱利的话：“数学家能从咖啡中喝出定理。”就有这么一杯特别幸运的咖啡，它引出了一个被广为引用的定理：如果每个人与至少一个客人结识，很快所有人都将喝到那瓶昂贵的葡萄酒。根据埃尔德什和莱利的观点，只需要30分钟，就能形成一个无形的社会网络，将房间内所有的客人联系起来（如图2-2所示）。一名客人听说昂贵葡萄酒的消息后，过不了几分钟，就会发现那瓶酒只剩下一个空瓶了。

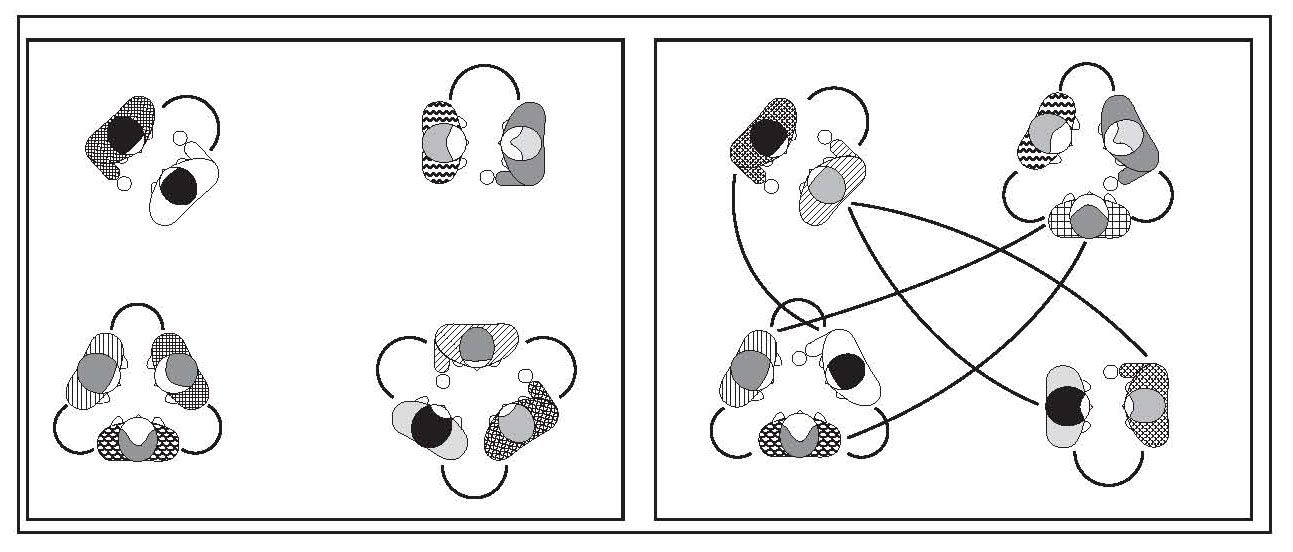
在一个有10位客人的聚会上，人们起初互不相识。但当他们开始分成小组交谈，他们之间便形成了社会链接。最初，各个组是彼此孤立的（左图）。事实上，虽然同一个组内的客人之间存在社会链接（表示为实线），但是，不同组的客人彼此还是陌生的。但随着时间推移（右图），其中三位客人移动到其他的组，于是，一个巨大的节点簇出现了。虽然并不是任意两个人都互相认识，但是出现了一个包含所有客人的社会网络。沿着网络中的社会链接，任意两个客人之间都可以找到一条路径。

图2-2 聚会

世界是随机的吗

我们在鸡尾酒会上遇到的客人是欧拉创立的数学分支——图论中一个问题的一部分。客人是节点，每次邂逅会在客人之间创建一条社会链接，于是就形成了一个相识关系网络，也被称为图——通过链接连接起来的一簇节点。图的例子很多：计算机通过电话线连接，我们体内的分子通过生化反应连接，公司通过贸易关系连接，神经元通过轴突连接，岛屿通过桥梁连接。无论节点和链接是什么，无论它们的性质如何，对于数学家而言，它们都是同一样的东西：图或者网络。

虽然简化图看起来很优美，但是把所有的网络简化为图却将面临一些巨大的挑战。社会、互联网、细胞或大脑都可以用图来表示，但它们之间存在明显的差异。很难想象人类社会和细胞之间能有多少共通之处。在人类社会中，我们通过随机邂逅和有意识的决定结交朋友，而在细胞中，无情的化学和物理规则支配着分子间的所有反应。对于自然界里的各种网络而言，支配其链接形成的规则肯定也会截然不同。表面上看，寻找一个能够描述所有这些不同系统的模型，似乎是一个难以逾越的挑战。

然而，科学家们的终极目标，就是为极其复杂的现象寻找最简单的可能解释。埃尔德什和莱利接受了这个挑战，并就在同一个框架下描述所有的复杂图这一问题，给出了一个优美的数学解答。由于不同的系统按照完全不同的规则构建各自的网络，所以埃尔德什和莱利谨慎地忽略这种多样性，提出了一个自然界可能遵循的最简单的解答：随机连接节点。他们认为，创建网络最简单的方式是掷骰子：选择两个节点，如果掷出的是6，就在节点之间放置一条链接。如果掷出的是其他数字，就不连接这两个节点，转而选择另外一对节点重新开始。因此，埃尔德什和莱利认为，图和其代表的世界从根本上讲是随机的。

埃尔德什喜欢说：“有一个古老的争论，是人类创造了数学，还是人类只是发现了数学。换句话说，真理在我们知道它之前就已经存在了吗？”对于这个问题，埃尔德什给出了明确的答案：数学真理和其他绝对真理一样，都是客观存在的，我们只是重新发现了它。随机图理论是如此的优美而简单，在埃尔德什看来，它是永恒的真理。不过，我们现在知道了，随机网络在我们宇宙的组织中发挥的作用很少。相反，自然界所依靠的那些根本规则，是我们将在随后的章节中介绍的。而埃尔德什本人通过发展随机图理论创造的数学真理，则为我们提供了一个观察世界的视角。埃尔德什并不了解自然界创造大脑和社会的规则，他只是做出了大胆的假设，认为上帝喜欢掷骰子。他的朋友，普林斯顿的阿尔伯特·爱因斯坦却相信相反的观点：“上帝从不掷骰子。”

从节点到节点簇

现在，我们回到鸡尾酒聚会，做一些随机图理论的练习。开始时，我们有大量孤立的节点，然后我们模仿客人间的随机邂逅，在节点之间随机地添加链接。如果只添加少数几个链接，唯一的结果是一些节点通过链接形成了配对。如果继续添加链接，一些配对将不可避免地连接在一起，形成包含几个节点的簇。当添加了足够多的链接使每个节点平均拥有一个链接时，奇迹出现了：一个独一无二的巨大节点簇出现了。也就是说，大多数节点都是这个节点簇的一部分，无论从哪个节点出发，沿着节点间的链接前行，都能够到达大多数其他节点。这个时刻就是你那瓶昂贵的葡萄酒不再安全的时候，因为巨大的节点簇使得葡萄酒的消息可以传递到每一个人。数学家们将这个现象称为巨大连通分量的涌现，巨大连通分量中包含了大部分的节点。物理学家把这个现象称为渗流（percolation），并把巨大连通分量的涌现称为相变（phase transition），这和水结成冰的瞬间是类似的。社会学家们会说，客人这时刚好形成了社区。

链接洞察

尽管不同的学科有不同的术语，但他们一致认为，随机选择网络中的节点对进行连接时，会出现一些特殊的现象：当添加的链接数超过一个临界值时，网络将发生剧烈变化。在到达这个临界值之前，网络中包含许多不连通的小节点簇，每个节点簇对应只在内部进行交流的一组人。到达临界值之后，网络中将出现一个巨大的节点簇，几乎所有人都被连接在这个巨大的节点簇里。

每个人只需认识一个人，就能形成社会

每个人都是遍及全世界的社会网大节点簇的一部分，没有人能游离在外。没有人能够认识地球上其他所有人，但是，在人类社会网络中，任意两个人之间一定有一条路径。类似地，我们大脑中的任意两个神经元之间、世界上任意两个公司之间、我们体内的任意两种化学元素之间都存在可达路径。任何事物都无法脱离这个高度互联的生命网络而独立存在。保罗·埃尔德什和阿尔弗雷德·莱利告诉了我们这背后的原因：每个节点只需要一个链接就可以使它和整个网络保持连接。这意味着，要和网络中的其他成员保持连接，每个人只需要认识一个人，大脑中的每个神经元和其他神经元之间只需有一条链接，我们体内的每种化学元素只需具备参与至少一个化学反应的能力，商业世界中的每个公司只需和至少一个其他公司建立贸易关系。“1”是这里的阈值。如果节点拥有的平均链接数少于1，网络将破碎成相互间没有联系的小节点簇；如果每个节点拥有的链接数超过1，网络就可以远离破碎的危险。

自然界中，节点的平均链接数经常大大超过阈值1。据社会学家估计，每个人认识的人数在200到500之间。每个神经元平均和几十个其他神经元相连，有的神经元则和数千个神经元相连。每个公司通常和数百家供应商和客户公司有链接，一些大公司会有多达上百万个链接。在我们体内，大多数分子参与的化学反应远不止1个，像水这样的分子参与了数百个。因此，真实网络不仅是连通的，而且远远超过了保持连通所需的阈值1。

随机网络理论告诉我们，当节点的平均链接数增加到超过临界值1时，游离在巨大节点簇之外的节点数成指数下降。也就是说，添加的链接数越多，越难找到保持孤立的节点。自然界不会冒险停留在阈值附近，而是远超过了阈值。如此一来，我们身边的网络不再只是一些孤立的小网络，它们的连接非常稠密，没有人游离在网络之外，每个节点皆可到达。这就解释了，为什么根本没有人能够完全游离在社会之外，为什么我们体内的所有分子融在同一个复杂的细胞网络中，为什么传教士保罗的教谕能够到达他没有见过的人那里，为什么MafiaBoy能够成为报纸头条。答案是：沿着网络中的链接，个体的行为很容易就会影响到数百万人。

改变图论的历史

埃尔德什和莱利发现的相变或渗流的特殊时刻，即巨大的节点簇涌现的时刻，是图论发展过程中的重大事件。这一发现之所以重要，不仅因为它做出了令人难以相信的预言——每个人只需要认识一个人就能形成社会，更因为它改变了图论研究的历史。在埃尔德什和莱利之前，图论从没有研究过鸡尾酒聚会、社会网络或随机图。图论几乎一直在关注规则图，这类图的结构中没有不确定性。然而，一旦涉及复杂系统，譬如互联网或细胞，规则图就不再是常态，而变成了特例。埃尔德什和莱利第一个指出，从社会网络到电话网络，真实的图都不是漂亮的规则图，而是极其复杂的。鉴于这些网络的复杂性，埃尔德什和莱利假定这些网络是随机的。

回顾历史，我们不再感到奇怪：居然是埃尔德什和莱利这对看似不太可能的数学家，通过引入随机性改变了数学这一受人尊敬的领域。因为偶然和随机在他们两人的生活中占了很大的分量。虽然莱利比埃尔德什小7岁，但他们的父母在布达佩斯早就相识，这也是二人能够结识的原因。1948年，他们在阿姆斯特丹偶然相遇，从此开始合作。在此之前，他们都有着相当不平静的经历。名额控制条令（Numerus Clausus）限制了大学招收犹太人的数量，所以莱利高中毕业后只好到一家修船厂工作。后来，他在数学竞赛和希腊语竞赛中胜出，于1939年获准进入大学。拿到数学学位不久他就被征为苦力，不过他逃脱了。

埃尔德什和他的同事都了解莱利在战争期间的反抗行为，而且非常敬佩和尊重他。

莱利曾勇敢地乔装成匈牙利的法西斯分子，帮助他的朋友从集中营中逃脱。据说，莱利穿着法西斯战士的服装，潜入布达佩斯犹太人集中营，设法救出了他的父母。他用伪造的证件在纳粹控制的布达佩斯生活了数年。只有了解纳粹恐怖主义实际情况的人，才能真正体会到莱利做这些事需要多大的勇气。

毫无疑问，在战争结束之前，莱利的数学才能无法充分发挥。直到1946年搬到了列宁格勒，他才能继续他的研究。在列宁格勒，他的创造力爆发了。虽然俄语水平有限，但他在很短的时间内就学习和掌握了数论，而且还就数论中的著名难题哥德巴赫猜想证明了一些根本定理。因此，当莱利在两年后的阿姆斯特丹碰到埃尔德什时，他的身份不再是一个有抱负的青年数学家或是一位家庭世交，而是一位享誉国际的著名科学家。

那时候，埃尔德什已经为自己贴上了旅行数学家的标签。他经常突然出现在同事家的门口，声称“我的大脑对外开放”，并邀请同事和他一起不知疲倦地探讨数学问题。他唯一一个永久职位是由位于印第安纳州南本德的圣母大学提供的，该校数学系的主任阿诺德·罗斯（Arnold Ross）邀请埃尔德什担任客座教授，条件很宽松：埃尔德什可以来去自由，他不在的时候，由他的助教帮他授课。

那时的圣母大学是一个天主教文理学院，还没有像几十年后那样享有盛誉。尽管如此，圣母大学为埃尔德什提供了一个安静而舒适的工作环境，在那里，埃尔德什可以经常和他的神父同事进行讨论。他对宇宙和神有着独特的视角，他很享受在圣母大学的时光。有一次，被问到在圣母大学的那段时光时，埃尔德什半开玩笑地说：“那里的加号（这里指好处）太多了。”因为学校里有太多的十字架。当圣母大学后来想让埃尔德什转为终身教职时，他委婉地拒绝了。或许，他不愿意失去生活的随机性和不可预测性。

平均值主导的随机宇宙

埃尔德什和莱利在阿姆斯特丹的相遇，是他们亲密友谊和合作的开始。他们共合作发表了30多篇著作，直到1970年莱利49岁英年早逝。这些著作中，有8篇论文是关于图论的。第一篇论文发表于在阿姆斯特丹相遇的10年后，该论文首次研究了“图是如何形成的”这一重要问题。该论文最明显的特点是，他们用随机性来处理图论问题，研究网络中节点拥有的边数。正则图^[1]是独特的，图中每个节点有完全相同的链接数。在简单的方形格中，相互垂直的线构成二维网格，每个节点有4个链接；在蜂窝的六角栅格中，每个节点和其他三个节点相连。

随机图中则明显缺乏规则性。随机网络模型的前提便是高度平等：链接的放置是完全随机的。因此，所有节点有相等的机会获得链接。这和拉斯维加斯一样，每个人都有相等的机会中头奖。然而，每天结束的时候，只有少数几个赌徒能够赚到钱。类似地，如果我们在图中随机放置链接，有一些节点获得的链接会比其他节点多一些，还有一些节点的运气可能比较差，在一段时间内一个链接也没有获得。在埃尔德什和莱利描绘的随机世界里，慷慨和不公平并存：有些人穷，有些人富。然而，埃尔德什和莱利的理论告诉我们一个重要的预言：这种不公平的情况只是看上去会出现。虽然链接是完全随机放置的，但只要网络足够大，几乎所有节点都拥有差不多相同的链接数。

验证上述结论的一个办法是在聚会结束时询问所有客人他们在聚会时结识了多少人。等客人们都走了之后，我们便可以绘制一个直方图，画出有多少个客人新结识了一个人、两个人或者k个人。埃尔德什的学生贝拉·伯罗巴斯（Béla Bollobás）在1982年便精确地推导和证明了埃尔德什和莱利的随机网络模型直方图的形状。贝拉·伯罗巴斯是美国孟菲斯大学和英国剑桥大学三一学院的数学教授。其证明结果表明，随机网络模型的直方图服从泊松分布，而泊松分布的一些独特的性质会一直贯穿本书。泊松分布有一个明显的峰值，表明大多数节点所拥有的链接数和节点拥有的平均链接数一样。在峰值的两侧，泊松分布快速衰减，因此，与平均值偏离较大的值极少出现。

链接洞察

回到有60亿人口的社会中，泊松分布告诉我们，大多数人拥有的朋友和熟人的数量大致相同。根据泊松分布，朋友数量偏离平均值的人数随着其偏离程度成指数下降，很难找到朋友数明显多于或少于平均数的人。因此，随机网络理论预言，如果我们随机形成社会链接，最终会形成一个非常民主的社会，所有人都差不多，很少有人会偏离常态——非常善于交际或极度不合群。我们最终得到的网络有着非常平均的结构：均值就是常态。

埃尔德什和莱利的随机宇宙由平均值主导。大多数人认识的熟人数量大致相当，大多数神经元连接的其他神经元数量大致相当，大多数公司的贸易伙伴数量大致相当，大多数网站的访问人数大致相当。当自然界闭着眼睛抛洒链接时，长远来看，没有节点会被青睐，也没有节点会被歧视。

寻找复杂网络背后的秩序

埃尔德什和莱利的随机网络理论，自1959年提出以来，便一直主导着我们关于网络的科学思维。它创立的一些范式，在涉及网络的每个人的思想上打上了认识烙印。它把复杂性和随机性视为一回事。如果网络过于复杂，无法用简单的方式来刻画，我们不妨将它描述成随机的。毋庸置疑，社会、细胞、通信网络和经济都足够复杂，因此适用随机网络理论。

你可能会怀疑，宇宙真的是随机的吗？所有节点真的是平等的吗？如果我体内的分子随机地相互作用，我还能够写这本书吗？如果人们完全随机地相互影响，还会有民族、国家、学校、教堂以及其他形式的社会秩序存在吗？如果公司把售货员换成数百万个骰子，随机地选择客户，还会存在经济系统吗？大多数人都觉得，我们不是生活在随机世界里，这些复杂系统背后一定存在某种秩序。

那么，为什么埃尔德什和莱利这样世间罕见的智者选择将网络涌现建模成完全随机的过程呢？答案很简单：他们从没有打算提出一个网络形成的通用理论。他们更多地着迷于随机网络的数学之美，而没有关注模型忠实表达网络特性的能力。在他们1959年那篇开创性论文中，他们的确提到“图的演化可能是某种通信网（铁路、公路、电力网络系统等）演化的一个相当简化的模型。”但是，除了这次对真实世界的偶尔涉足之外，他们在该领域的工作，与应用几乎没有任何关系，完全受他们对有关问题数学深度的好奇的鼓舞。

埃尔德什会第一个赞同我们的观点：真实网络的组织原则，有别于他在1959年提出的随机网络模型。但是，这对他而言无关紧要。通过使用随机性假设，他打开了通向新世界的窗口，其数学之美和一致性是后续图论工作的主要推动力。

直到最近，我们还没有找到替代的模型来描述我们互联的宇宙。因此，随机网络一直主导着我们关于网络建模的观点。从根本上讲，复杂的真实网络被视为随机的。

埃尔德什善于提出好的问题，并推动其他人去求解这些问题。虽然他的生活十分简朴，只有旅行时经常随身携带的小皮箱里为数不多的几件衣服，但是，如果别人为他感兴趣的问题提供了求解或证明方法，他会毫不吝啬地提供奖金。对于他认为简单的问题，奖励5美元，对于真正难解的问题，奖励500美元。如果你把证明提交给他，他很乐意支付奖金。一个1美元的问题经常会比500美元的问题还要难。不过没有关系，有幸赢得奖金的数学家从不会去兑现他们收到的支票。大多数人会把支票装裱起来，因为这种奖励是那个世纪最杰出的天才给出的独特肯定，无论多少金钱都不能和这种奖励的精神价值相提并论。

让我们仿照埃尔德什的方式，问一个他没有碰过的问题。真实网络长什么样？以这样一种不严谨的方式提出问题无法令埃尔德什满意。这个问题太宽泛了，甚至可能没有唯一的解答，而且我们很可能永远也不能给出严格的证明。因此，这个问题不可能出现在《超限》（Transfinite Book）这本书中——这本并不存在的书是埃尔德什理想中的一本书，他认为只有好的数学证明和定理才能出现在这本终极著作中。虽然我们提出的这个问题可能无法赢得埃尔德什的认可，但在随后的章节里我们会看到，在数学世界之外，这个问题有着深远的影响。

[1] 正则图是指各顶点的度数均相同的无向简单图。——编者注