模块化，补上无尺度网络缺失的一链

2001年可能是我一生中最忙碌的一年，这一年由两个同样紧迫的项目主导着。第一，《链接》占据了我每天的写作计划，一般从早上6点开始，直到晚上很晚才结束。第二，我的合作者，来自美国西北大学的生物学家佐尔丹·沃特建议我们继续探索小世界的神秘之处——枢纽节点和模块之间的根本矛盾。在写作一本大众书籍的同时进行科学研究相当具有挑战性。2001年夏天，将枢纽节点和模块进行统一的首次尝试开始了。我和研究组的博士生伊丽莎白·拉瓦茨（Erzsébet Ravasz）、我在布达佩斯厄特沃什·罗兰大学的论文导师塔马斯·维则克（Tamás vicsek）一起构建了一个小模型，指出了无尺度网络和模块化网络的融合可能。

为了构建模块化的网络，我们从单个节点（如图16-1A）开始，将其复制三份，让这些复制出的新节点和老节点连接起来，并让新节点之间彼此相连，得到了一个小的四节点模块（如图16-1B）。我们接下来将该模块复制三份，将新模块的外围节点和老模块的枢纽节点相连，从而得到一个包含16个节点的网络（如图16-1C）。继续进行这样的“复制-连接”操作，节点数目变成原来的四倍，得到一个包含64个节点的网络（如图16-1D）。虽然我们可以无限地继续进行该过程，但我们停在了这里，开始检查该网络的结构。

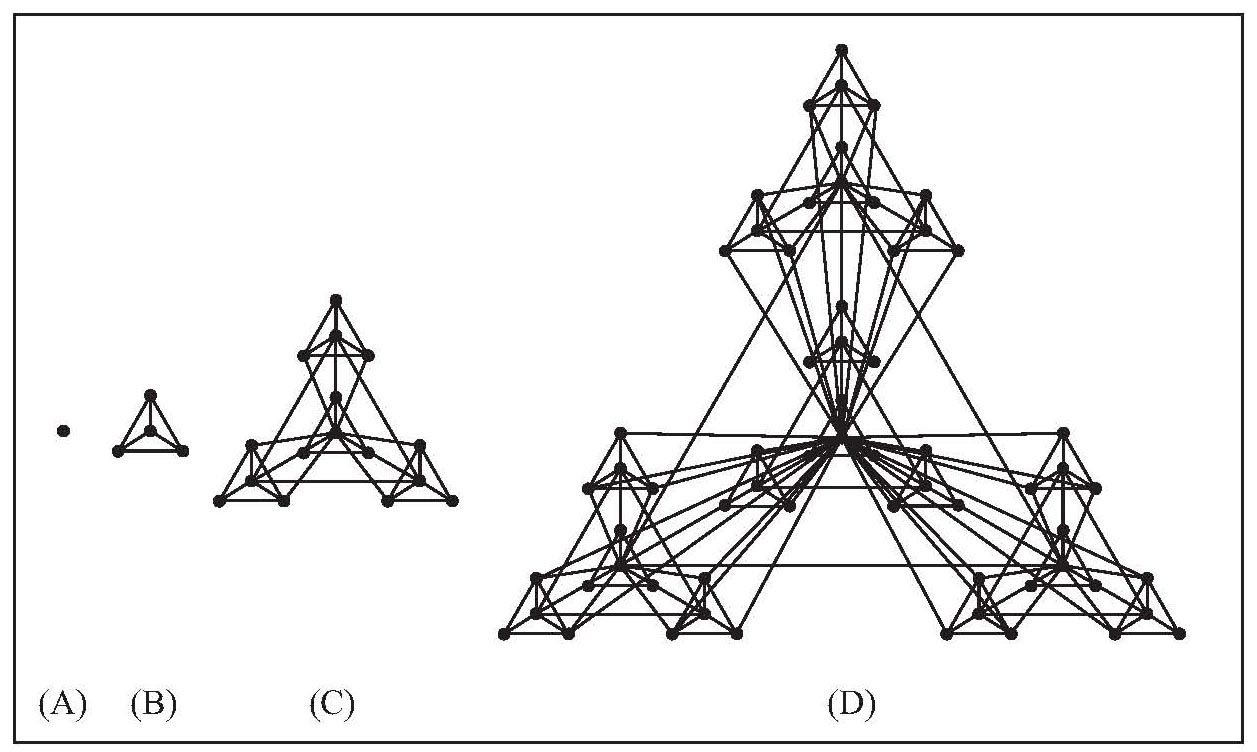
从单个节点（A）开始，通过复制得到三个新节点，然后将新节点和老节点连接起来，新节点之间也彼此连接，从而得到（B）中所示的具有4个节点的结构。下一步，我们将这个包含4个节点的结构（即模块）复制三份，放置在老模块的周围，将新模块的外围节点和老模块的枢纽节点相连，将新模块的枢纽节点彼此相连。我们得到的网络包含16个节点，如（C）所示。我们可以重复同样的过程，将模块C复制三份，放在老模块的周围，将新模块的外围节点和老模块的枢纽节点相连，让新模块的枢纽节点彼此相连，从而得到（D）所示的网络。这个过程可以无限次进行下去，每次产生一个相当于老网络4倍大的新网络。最终得到的网络是无尺度的：我们可以清楚地看到节点间的层级，很多小节点通过少数大的枢纽节点连接在一起。同时，这个网络也是模块化的，这些逐渐变大的模块之间形成了一个层级。实际上，我们很容易将（C）中的网络分解成16个4节点模块，或者4个16节点的模块。该网络具有一个有趣的性质，即它显现出层次化的聚团性：该网络由许多高度连接的4节点模块构成，这些模块形成连接程度稍低的16节点模块，后者是连接更松散的64节点模块的组成构件。最近我们意识到，这种层次化的聚团性是很多真实网络的普遍性质，包括细胞和万维网。

图16-1 我们生成的具有层级的网络

首先，该网络的构造过程使其是模块化的：最底层是很多高度连接的四节点模块，这些模块是更大的16节点模块的构件，后者又是64节点网络的主要组成部分。其次，一个具有39条链接的高度连接的枢纽节点将网络连接在一起。16节点模块的枢纽节点是稍小的局部枢纽节点，具有14条链接。大量只有少数链接的节点伴随着这些枢纽节点，形成我们熟悉的层级，很多小节点通过少数大的枢纽节点连接在一起，这是无尺度网络的特征。实际上，恰好拥有k条链接的节点数目服从幂律分布，证实了该模型的无尺度性质^[1]，而且该模型将格兰诺维特的朋友圈和枢纽节点成功统一在了一起。

无尺度模型对于我们理解复杂网络具有重要作用，它首次解释了刻画真实网络的幂律。这个新模型提供了缺失的一链：模块化的无尺度网络。但是，我们如何测试该模型是否准确地再现了真实系统的模块性呢？这正是我们提出该模型之后一直在思考的问题。由于未能很快找到答案，我们于2002年7月将一篇简短的论文放到了Los Alamos preprint数据库，该论文包含了这个新模型的早期版本。五个月后，我们还在思考我们的问题时，在葡萄牙的波尔图一起工作的谢尔盖·多罗格夫特瑟夫（Sergey Dorogovtsev）、A·V·戈尔特瑟夫（A.V.Goltsev）和何塞·孟德斯（José Mendes）张贴出一个在线的简短论文，补上了我们期待很久的缺失环节。

模块性的量化度量是聚团系数（在第4链讨论过），聚团系数告诉我们一个节点的邻居之间的连接程度。对于一个给定的节点，如果它的所有邻居都彼此互联，那么它的聚团系数就等于1。如果所有邻居都互不相连，聚团系数就是0。^[2]枢纽节点和幂律的发现，迫使我们放弃了埃尔德什和莱利的民主乌托邦——大多数节点拥有相同数目的链接，转向了由少数枢纽节点主导的无尺度世界。

关于模块，我们也将经历类似的范式转换。实际上，对于随机网络和无尺度网络，小节点和枢纽节点具有同样的聚团系数，聚团性均匀地分布。在前面讨论的模型中，波尔图三人组得出了一个完全不同的结论：节点的连接度越高，聚团系数越小。^[3]更特别的是，他们发现模块的聚团系数服从严格的幂律，^[4]拥有k条链接的节点，其聚团系数按照k的倒数的方式衰减。这大大偏离了无尺度网络模型和随机网络模型的预言——对于这两个模型而言，聚团系数独立于k。由于聚团系数很容易测量，这个新的幂律为我们研究真实网络的模块性提供了强大的工具。

由于我们关于模块性的最初思考源于我们期望能够理解细胞的内部组织方式，佐尔丹·沃特、伊丽莎白·拉瓦茨和我首先研究了43个生命体的新陈代谢。对于每个生命体，聚团系数都服从模型所预言的幂律。因此，细胞不仅是模块化的，而且其模块性具有严格的架构：大量较小但是连接度高的模块以层次化的方式结合成少数较大但是连接度较低的模块。在细胞中没有典型的、有代表性的模块。相反，新陈代谢既可以分解成很多小的、高度连接的模块，也可以分解成少数几个较大的、但是连接不太紧密的模块。层次化的模块性揭示了枢纽节点的新作用：枢纽节点维持模块间的通信。小的枢纽节点连接着一些较小的模块内的节点。大的枢纽节点就像大公司的CEO，管辖着大多数的部门和模块，是不同大小、不同文化的社区之间的桥梁。

链接洞察

层次化的模块性具有显著的设计优势：它允许系统的各个部件各自进行演化。实际上，汽车制造商不需要重新构建引擎就可以提高汽车的变速器，芯片设计者不需要考虑键盘或光驱就能构建出更快的处理器。在自然系统中，模块性允许各个功能分别进行演化。实际上，基因突变一次最多影响少数几个基因，其造成的影响局限于少数几个模块。如果某次突变是一种提高，具有更优模块的生命体会繁荣起来。但是，如果某次基因突变降低了模块的适应度，生命体最终无法生存。

前面讨论的层次化模块性绝不局限于细胞。重新读一下最近关于网络的文献，我们意识到，模块性的量化特性在之前已经被观测到了。来自瑞士日内瓦大学的让-皮埃尔·艾克曼（Jean-Pierre Eckmann）和来自以色列魏兹曼科学研究所的艾丽莎·摩西（Elisha Moses）观察到万维网上的聚团系数服从幂律，并且说道：“尽管尺度是让人吃惊的，但我们还不知道尺度的原因。”后来看来，他们的发现为万维网的层级架构提供了直接的证据。例如，有关库尔特·冯内古特（Kurt Vonnegut）或菲利普·罗斯（Philip Roth）的网页形成了小社区，这些小社区以一种层级的方式嵌套在更大的关注美国文化的网页组中。类似地，阿列克谢·巴斯克斯、罗莫尔多·帕斯特-赛托拉斯和亚历山德罗·维斯皮那尼发现，域级的互联网地图具有层级组织形式，体现为服从幂律的聚团系数。我们的测量表明，语言的同义词网络同样具有层级，像“turn”、“take”或“go”这样少数几个高度连接的词，每个都有上百个同义词，将不同词义的模块连接在一起。蛋白质交互网络的层次化模块性提供了另一个生物方面的例子，将枢纽蛋白质的作用重新解释为不同功能模块之间的中介。因此，层次化的模块性是大多数真实网络的普遍性质，伴随着无尺度架构存在。

正是这种层次化模块性使得多任务有了可能：每个模块内部的稠密链接有助于具体任务的高效完成，枢纽节点协调多个并行功能之间的通信。当同一个模块同时面临多个任务时，瓶颈和减速是不可避免的。计算机依赖单个中央处理器，这是它的主要瓶颈。当我们的大脑皮层需要处理多个任务时，我们的处理速度也会变慢。

[1] 对于前面描述的构造过程，度分布服从p（k）～k^-η，这里η=l+ln4/ln3=2.26。

[2] 拥有k条链接的节点，其聚团系数定义为C（k）=2N（k）/k（k-1），其中，N（k）表示该节点的k个邻居之间的直接链接数。

[3] 四节点模块（如图16—1B）的枢纽节点，其聚团系数等于1，因为它的三个邻居彼此相连。16节点模块（如图16—1C）的枢纽节点具有稍差的聚团性：它的12个邻居之间只有12条链接，因此C=2/14。64节点网络的枢纽节点具有更小的C：它的39个邻居之间仅有39个链接（如图D），因此C=2/38。

[4] 波尔图小组证明，拥有k个链接的节点，其聚团系数C（k）以C（k）～k^—1的方式依赖于k。