第4链 小世界

无论是找工作、获取消息、开餐馆，还是传播新潮流，弱关系在我们和外部世界互通消息方面发挥着至关重要的作用。弱关系，是我们连接外部世界的桥梁。然而，聚团现象无处不在，它已经从社会的独特性质迅速提升为复杂网络的普遍性质。

“小世界”

网络“小世界”网络是一类特殊的复杂网络结构，在这种网络中，大部分节点彼此并不相连，但节点之间经过少数几步就可到达。

聚团性

聚团性是指在网络中，同一个顶点的邻点之间有更大的概率有边连接的现象，简单来说，就是我们的密友之间往往也是朋友。它是复杂网络拓扑的一个重要特性，源于小世界网络模型，通常都用聚团系数来衡量。聚团系数能够说明你朋友圈的连接紧密程度。如果聚团系数接近1，则你所有的朋友之间也是朋友；如果聚团系数是0，那你便是将你的朋友圈连在一起的唯一的人，他们彼此不认识。

格兰诺维特与“弱关系的优势”

马克·格兰诺维特（Mark Granovetter）把自己第一篇论文稿件提交出版时，还只是哈佛大学的一名研究生，但他对自己的稿件抱有很高的期望。20世纪60年代后期的哈佛大学可谓独得天时地利。那时，关于网络的思想正在社会学中滋生，而哈佛大学和麻省理工学院正是这种新思想的温床。哈里森·怀特（Harrison White）是当时社会学中提倡网络视角的先锋人物，他的一系列报告让格兰诺维特在研究生初期便接触到社会网络。事实证明，很多新想法在格兰诺维特的博士论文中找到了有利于其生长的肥沃土壤。

在博士论文中，格兰诺维特从微观社会学的角度研究了“人们是如何找到工作的”。这是每位研究生迟早都要面临的问题。格拉诺维特没有选择去修改简历和参加招聘会，而是渡过查尔斯河去了马萨诸塞州的牛顿镇。现在的牛顿镇是波士顿的一个富庶郊区，但在20世纪60年代后期，那里还是工薪阶层的居住区。为了弄清楚人们是如何利用社会关系网络找到新工作的，格兰诺维特走访了数十位从事管理工作和技术工作的工人，询问他们现在的工作是在什么人的帮助下获得的。是朋友介绍的吗？他得到的回答是相同的：不，不是朋友介绍的，帮忙介绍工作的人只是一般的熟人。这让格兰诺维特想到了化学课上学到的内容：弱的氢键是如何将巨大的水分子结合在一起的。自他刚上大学起，这部分知识就深深印在了他的脑海里。他从中得到灵感，写出了第一篇论文。

在这篇很长的论文中，他揭示了弱社会关系在我们生活中的重要性。1969年8月，他把论文寄给了《美国社会学评论》（American Sociological Review）。12月，他收到了回信，两名匿名评审人拒掉了他的论文。其中一位评审人评价道：“阅读该稿件时，我的脑子里就立即浮现出很多该稿件不适合发表的理由。”格兰诺维特非常沮丧，他在随后的三年内都没有再去碰这篇论文。直到1972年，他将稿件稍微缩短后，投到另外一个期刊《美国社会学期刊》（American Journal of Sociology）。这一次他的运气不错，论文最终于1973年5月发表了，此时距他第一次投稿已经过去了4年。今天，格兰诺维特的论文《弱关系的优势》（The Strength of Weak Ties）被公认为最有影响力的社会学论文之一。该论文也是被引用次数最多的论文之一，它在1986年被期刊题录快讯数据库（Current Contents）评为经典引用论文。

在《弱关系的优势》中，格兰诺维特提出了一个乍听起来很荒谬的观点：无论是找工作、获取消息、开餐馆，还是传播新潮流，弱社会关系比我们所珍视的强社会关系更重要。他指出，每个普通人周围的社会网络结构（他称之为Ego，即以自己为中心的社会圈）相差无几。

社会圈里有一些关系亲密的朋友，他们中的大多数人相互之间也有联系，从而形成一个稠密的社会结构。同时，社会圈中还有一些关系一般的熟人，这些人一般互不相识。不过，这些熟人各自也有自己的好朋友，他们同样形成一个稠密的社会结构，只是这个社会结构没有出现在前面的社会圈里。

格兰诺维特的观点背后，有一幅与埃尔德什和莱利描述的随机宇宙迥然不同的社会图景。在他眼中，社会结构是一个个高度连接的簇，或者一个个紧密联系的朋友圈，圈子里的人都相互认识。少量的外部链接将这些圈子与外面的世界连在一起，使其不至于与世隔绝。如果格兰诺维特的描述是正确的，人类社会的网络结构将非常奇特。它将由一些完全图^[1]构成，在完全图中，每个节点都和内部其他节点相连（如图4-1所示）。这些完全图通过一些弱关系连接在一起，弱关系体现了不同朋友圈之间的熟人关系。

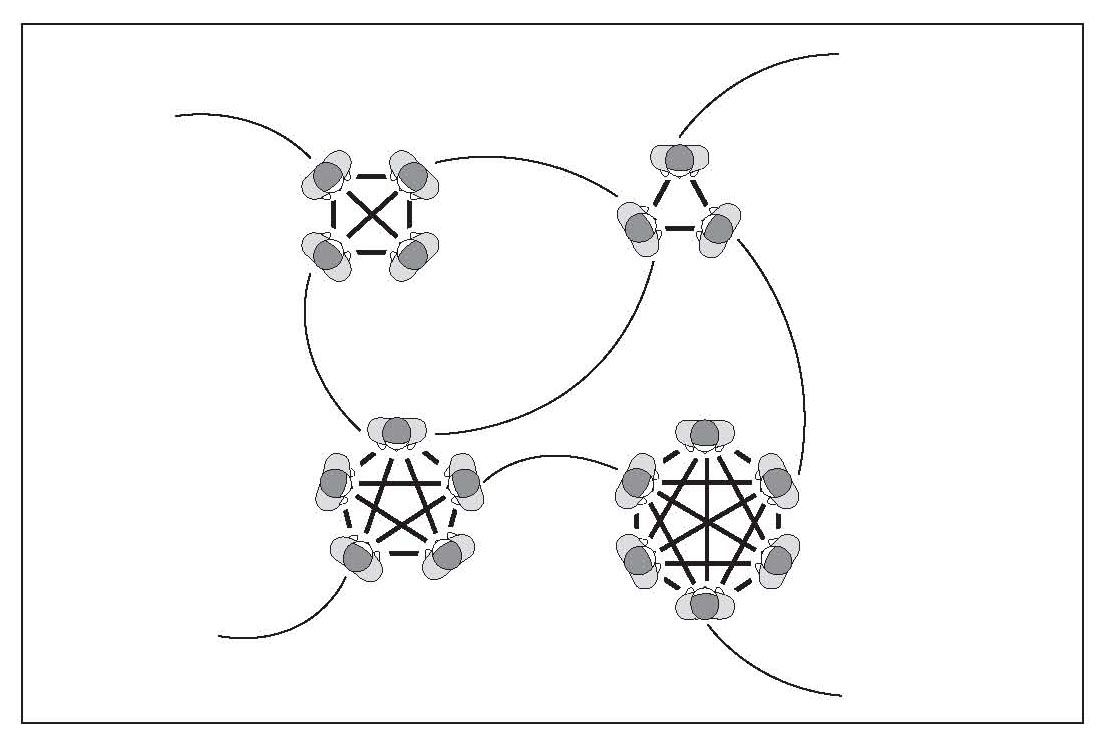
在马克·格兰诺维特描述的社会中，我们的密友相互之间往往也是朋友。这样一个聚团化社会的背后，社会网络由一些完全相连的小朋友圈组成，朋友圈内部的关系是强关系，用粗线条表示。细线条表示的弱关系将朋友圈里的人和他们的熟人连接起来，这些熟人也有着自己的朋友圈。无论是散布谣言，还是找工作，弱关系在很多社会活动中都扮演着重要角色。

图4-1 强关系和弱关系

链接洞察

弱关系在我们和外部世界互通消息方面发挥着至关重要的作用。在找工作的时候，我们的密友往往帮不上忙。因为他们和我们处在同一个圈子里，他们接触的信息和我们一样。为了获取新信息，我们必须使用弱关系。事实的确如此，对管理岗位的工人而言，在获得职位信息时，通过弱关系获得信息的可能性（27.8%）要大于通过强关系获得信息的可能性（16.7%）。弱关系，或熟人关系，是我们连接外部世界的桥梁。这些人和我们在不同的地方活动，因此，我们能够从他们那里获取到从密友处无法获得的信息。

随机网络中没有朋友圈，因为我们和其他节点之间的链接是完全随机的。在埃尔德什和莱利的社会宇宙中，我的两个密友相互认识的可能性，与某个澳大利亚鞋匠和某个非洲部落酋长是好朋友的可能性是一样的。但是，我们的社会看上去并不是这样的。在大多数情况下，两个好朋友也分别认识对方的朋友，因为他们经常参加相同的聚会，出入相同的酒吧，观看相同的电影。两个人之间的关系越强，他们的朋友圈相互重合的程度越大。虽然格兰诺维特关于弱关系重要性的观点乍看上去似乎与直觉不符，甚至有些荒谬，但它揭示了我们社会组织结构的一个简单的事实。在格兰诺维特描述的社会中，内部完全连接的朋友圈通过弱关系形成一个支离破碎的网络，这比埃尔德什和莱利提出的完全随机的社会图景更接近我们的日常生活体验。为了完全理解社会的结构，随机网络理论需要以某种方式和格兰诺维特描述的聚团现象结合起来，而实现这样的结合花费了将近30年的时间。有趣的是，解决这一问题的线索并不是来自社会学或图论。

趋同与聚团

在中央咖啡馆对面，距离卡林西最喜欢的窗口仅几步之遥，穿过一扇小小的门，走过窄窄的地下室楼梯，你便可以进入布达佩斯最高档的一座剧院。该剧院的名字或许是“密室”（Kamra），因为它的舞台只能容纳约10名演员，台下只能坐100名观众。然而，如果你熟悉布达佩斯繁荣的剧院生活，你一定渴望能到此一坐。我上一次在这里观看演出时，剧院为了节省空间撤掉了幕布，观众只能靠猜测来判定每一幕结束的时刻。不过不用担心，结束时刻其实很难错过。因为那时候，观众席会突然爆发出雷鸣般的掌声，掌声经过地下剧场乌黑墙壁的反射，不断放大。很快，混乱的掌声变成了有节奏的掌声。大家的手掌精确地在同一时刻拍在一起，似乎有某种神秘的力量在召唤我们以相同的节奏鼓掌，就好像大家在随着无形的指挥棒鼓掌。演员鞠躬致谢，回到后台，然后再次亮相。有节奏的掌声变得更响亮了。随着节奏的加快和力度的增强，掌声会暂时出现不同步的现象，但仅仅几秒钟后，就又汇合在一起。

同步的鼓掌并不是布达佩斯“密室”剧场所独有的。在东欧，这种现象在剧场演出、音乐会或体育赛事结束时经常出现，在世界各地也很常见。例如，1999年，在麦迪逊广场花园，当传奇冰球运动员韦恩·格雷茨基（Wayne Gretzky）从纽约流浪者队退役时，观众鼓掌向他致敬，起初无组织的鼓掌最终自发地变成同步的掌声。这种自发而神奇的同步鼓掌，是自组织现象的绝佳例子。自组织现象遵循着物理学家和数学家深入研究过的严格定律，某些种类的萤火虫也遵循这些定律。在东南亚，常有数百万萤火虫聚集在高大的红树林里，周期性地发光。突然，所有的萤火虫开始同时发光，同时变暗，将灯塔一样的树冠变成一个巨大的脉冲式电灯泡，几公里外都能看到。这种奇妙的趋同现象在自然界中非常普遍。例如，正是趋同现象让数千个心脏起搏细胞一起工作，使长期共同生活的女性具有趋同的月经周期。

20世纪90年代中期，邓肯·瓦茨正在康奈尔大学攻读应用数学博士学位，导师让他研究一个特别的问题：蟋蟀是如何同步鸣叫的？雄性蟋蟀通过大声鸣叫吸引雌性蟋蟀。和人类不同，为避免成为焦点，蟋蟀会仔细倾听周围其他蟋蟀的鸣叫，来调整自己的发声，以便和邻居的鸣叫声混在一起。把很多蟋蟀放在一起，混乱的鸣叫很快便汇成和谐的交响曲，在潮湿夏夜的门廊中，我们经常可以听到这样的交响曲。

瓦茨不是那种书呆子式的学究数学家。他思维敏捷，具有超强的反思能力，因此能够停下来甚至退一步去反思自己的工作，并在必要时调整方向。例如，对于蟋蟀的研究让他变成了一名社会网络的研究生，并最终成为一名社会学家。2000年，哥伦比亚大学社会学系聘请他为教授，这意味着他正式转型为社会学家。

当瓦茨致力于研究蟋蟀如何同步时，他对六度分隔概念产生了浓厚的兴趣。六度分隔的概念是他父亲在闲谈时偶尔提及的，却深深印在了瓦茨的脑海里。一直以来，人们对六度分隔这样的说法都抱有很大的兴趣，但这种在咖啡馆里谈论的事情一直没有经过仔细的研究。瓦茨认为，要完全理解蟋蟀是如何同步的，必须先理解它们是如何关注其他蟋蟀的。所有的蟋蟀都在倾听彼此的鸣叫吗？或者，有些蟋蟀会选择一个自己喜欢的蟋蟀，然后努力和它喜欢的蟋蟀保持同步？蟋蟀或者人类相互影响的网络结构是什么样的呢？瓦茨发现，自己对网络的兴趣越来越浓厚，对蟋蟀却渐渐失去了兴趣。他向导师史蒂文·斯托加茨（Steven Strogatz）寻求建议。斯托加茨是康奈尔大学的应用数学教授，在混沌和同步的研究方面成果卓著，他不会让任何新奇的想法从身边溜走。很快，他们就开始探索前人尚未涉及的研究领域，他们研究的网络超越了埃尔德什和莱利的随机网络边界。

瓦茨在网络领域的研究之旅开始于一个简单的问题：我的两个朋友相互认识的可能性有多大？我们从前面了解到，在随机网络理论中，这个问题的答案很清晰：由于节点是随机连接的，我的两个好朋友相互认识的可能性，和威尼斯船夫与爱斯基摩渔夫认识的可能性是一样的。很明显，正如格兰诺维特在25年前指出的，这不是社会的实际运行情况。

链接洞察

实际情况是，我们都是某个节点簇的一部分，同一个节点簇里的人相互认识。因此，我的两个好朋友必然也相互认识。为了找到社会聚团特性的证据，并让数学家和物理学家接受，我们需要度量聚团性。为此，瓦茨和斯托加茨引入了一个被称为聚团系数的量。假如你有4个好朋友。如果他们彼此也是朋友，两两之间存在一个链接，那么总共存在6个朋友链接。也有可能，你的一些朋友彼此不是朋友，那么他们之间的朋友链接数小于6，可能是4。在这种情况下，你的朋友圈的聚团系数是0.66，计算方式为：用你的朋友之间的实际朋友链接数4，除以他们之间最多能够形成的朋友链接数6。

聚团系数能够说明你朋友圈连接的紧密程度。如果聚团系数接近1，你所有的朋友相互之间也是朋友；如果聚团系数是0，你便是将你的朋友连在一起的唯一的人，其他人彼此都不认识。

格兰诺维特眼中的社会包含很多内部高度连接的节点簇，簇之间通过弱关系连接在一起。这样一个高度聚团的网络应该拥有很高的聚团系数。为了找到定量的证据证明社会是由很多节点簇构成的，我们需要度量地球上每个人的聚团系数。由于我们没有社会地图，无法得知谁和谁之间有联系以及谁和谁是朋友，所以度量每个人的聚团系数是不可行的。不过，有一个社会群体会定期发布他们的社会关系，因此我们可以研究这个社会群体的聚团系数。

埃尔德什数，高度聚团现象

如今，保罗·埃尔德什的名气不仅因为其提出了无数的定理和证明，还源于一个因他而起的概念：埃尔德什数。埃尔德什和507位作者合作发表过超过1500篇论文。能够成为他数百位合作者中的一员是无比荣耀的。除此之外，能够和他仅仅相隔两个链接也是很大的荣誉。为了记录与埃尔德什之间的距离，数学家们引入了“埃尔德什数”。埃尔德什自己的埃尔德什数是0。与他合作发表过论文的人，他们的埃尔德什数是1。与埃尔德什的合作者合作发表过论文的人，他们的埃尔德什数是2，依此类推。拥有一个小的埃尔德什数是一种荣誉，以至于1996年埃尔德什去世后，有人为了降低自己的埃尔德什数，涉嫌伪造和埃尔德什合作发表论文。全世界的数学家们一直，并且仍将继续争相找出自己和这个怪异的数学中心的距离。为了方便人们的查询，密歇根州罗契斯特市奥克兰大学的数学教授杰里·格罗斯曼（Jerry Grossmann）制作了一个网页，网页收集了数千名数学家的埃尔德什数，使所有发表过论文的数学家都能够计算出自己的埃尔德什数。

大多数数学家的埃尔德什数都很小，距离埃尔德什通常只有2到5步。但是，埃尔德什的影响远远超出了他所属的数学领域。经济学家、物理学家和计算机科学家也能很容易地和他联系上。

爱因斯坦的埃尔德什数是2；诺贝尔经济学奖获得者保罗·萨缪尔森的埃尔德什数是5；DNA双螺旋结构的发现者之一詹姆斯·D·沃森（James D.Watson）的埃尔德什数为8；著名语言学家诺姆·乔姆斯基（Noam Chomsky）的埃尔德什数是4；就连很少发表科学著作的微软创始人比尔·盖茨的埃尔德什数也只有4。我的埃尔德什数也是4：埃尔德什和约瑟夫·E·吉利斯（Joseph E.Gillis）合作撰写过论文，乔治·H·维斯（George H.Weiss）是后者的17名合作者之一，而维斯和我的博士生导师H·尤金·斯坦利（H.Eugene Stanley）合作过，我和斯坦利合著过一本书，并且一起发表过十几篇学术文章。

埃尔德什数的存在本身就表明，科学界形成了一个高度互联的网络，所有的科学家通过他们撰写的论文相互连接在一起。大多数的埃尔德什数都很小，这说明科学网络是一个真正的小世界。只有在极少数情况下，一部著作的作者才有可能互不相识，因此，论文合作关系体现了强社会链接。如此一来，科学网络可以看成社会网络的小规模原型，它的独特之处是所有链接定期发布。实际上，为了让研究人员能够找到特定主题的相关论文，所有的科学著作都记录在电脑数据库中。这相当于为科学家之间的社会和职业链接自动创建了一个详细的数字化记录。从而，我们可以利用这些数字化记录来研究合作网络的结构。

这正是我们的一个小组在2000年春所做的研究。在1999-2000学年，时任布达佩斯厄特沃什大学生物物理系特聘研究员兼系主任的托马斯·维谢克（Tamás Vicsek），组织了一个为期一年的关于生物物理的研究项目。该项研究在著名的中世纪布达城堡内的高级研究所内进行，城堡俯瞰多瑙河。来自罗马尼亚的物理学家佐尔丹·内达（Zoltán Néda）是项目的参与者之一，他还带来了欧塞贝特·洛瓦兹（Erzsébet Ravasz），后者当时是内达小组的一名研究生。匈牙利科学院的社会计量学专家安德拉什·舒伯特（András Schubert）也加入了这个研究团队，他能够将合作关系的大型数据库用于研究。我和维谢克、洛瓦兹、内达、舒伯特以及郑浩雄一起，用1991-1998年发表的论文，将这些数学家们连接在一起，形成了一个高度交织的网络。在该网络中，70975位数学家通过超过200000篇合作发表论文的链接连接在一起。假如数学家们是随机选择合作者的，根据埃尔德什和莱利的理论，最终形成的随机网络的聚团系数将非常小，大约为10-5。然而，我们的计算表明，实际合作网络中的聚团系数要高约10000倍，这证明了数学家们不是随机选择合作者的。相反，他们组成了一个高度聚团的网络，这种情形和格兰诺维特观察到的人类社会基本相似。

除了我们，圣塔菲研究所的物理学家马克·纽曼（Mark Newman）也一直在研究科学家合作网络，特别是物理学家、医学博士以及计算机科学家的合作网络。他研究的问题和我们在布达佩斯研究的问题相似。纽曼涉猎广泛，从随机系统到生态系统中的物种灭绝，都有涉及。纽曼认为，数字化的世界为我们完全理解网络提供了前所未有的机遇。在开始研究合作网络之前，他已经发表了好几篇关于小世界的论文，这些论文现在已经成为该方向的经典论文。当我们的计算机正在计算第一批结果时，纽曼在互联网上公布了关于科学家合作网络的第一篇论文。纽曼的论文证明，科学家的日常事务发生在稠密连接的科学家团体里，这些团体之间通过偶然的弱关系连接。他的研究工作和我们的一起，为我们一直以来感觉正确但在计算机出现之前难以测量的观点，提供了量化的证据。该观点是：社会系统中的确存在聚团现象。

聚团，复杂网络的普遍性质

我们可以直观地理解社会中的聚团现象。人类天生具有形成派系或团体的渴望，因为这能带来熟识、安全和亲密的感觉。但是，只有当社会网络的这个性质是自然界中大多数网络的普遍性质时，科学家们才会对其产生兴趣。因此，瓦茨和斯托加茨最重要的发现，是他们指出了聚团现象不只出现在社会网络中。

人们通常把自身的高智能归因于大脑中神经网络的规模和复杂程度。然而，线虫（Caenorhabditis elegans）提供了一个鲜活的例子，展示了302个神经元形成的神经网络所具有的智能。这种1毫米长的蠕虫虽然只有2到3周的生命，却非常出名。1962年，加利福尼亚大学伯克利分校分子科学研究所的著名分子生物学家悉尼·布伦纳（Sydney Brenner）把线虫作为分子生物学的实验小白鼠。自此以后，线虫出现在数千篇论文中，全世界有数百个实验室饲养它，并有一些专门介绍它的网页。

虽然线虫的基因组和人类没有太大的区别，它却是最简单的多细胞生物之一。实际上，科学家们已经成功弄清楚它神经系统中的具体连接方式，并绘制了详细的地图，展示神经元之间的连接关系。通过研究该神经元连接图，瓦茨和斯托加茨发现，这个小网络和人类社会整体上没有太大的区别：它也呈现出高度的聚团现象。它的聚团程度非常之高，实际上，神经元的邻居相互连在一起的可能性是随机网络的5倍以上。研究人员在研究美国西部电网时也发现了相同的模式，电网中的节点是通过电线连接在一起的发电器和变压器。好莱坞演员之间的合作网络也呈现出了这样的聚团现象，我们将在下一章详细讨论这个网络。

瓦茨和斯托加茨意外发现的聚团现象引起了大家的兴趣，科学界随后仔细研究了很多网络。现在我们知道，万维网中存在聚团现象；在计算机通过物理线路连接形成的互联网中，我们也观察到了聚团现象；在刻画公司通过合资关系形成的网络中，经济学家发现了聚团现象；在刻画生态系统中物种间捕食关系的食物链网络中，生态学家看到了聚团现象；细胞生物学家认识到，聚团现象解释了细胞网络的脆弱性。聚团现象无处不在，这一发现将聚团现象从社会的独特性质迅速提升为复杂网络的普遍性质，首次向“真实网络本质上是随机的”这一观点提出了严峻挑战。

高度聚团的代价，消失的小世界

为了解释大多数真实网络中普遍存在的聚团现象，瓦茨和斯托加茨在1998年发表于《自然》上的论文中，提出了一个新的模型，替代埃尔德什和莱利的随机网络模型。他们提出的新模型第一次把聚团现象和随机图的完全随机特性结合在一起。他们认为，人们生活在一个圈上（如图4-2所示），每个人只认识自己的直接邻居。在这个简单的模型中，每个节点有4个邻居，邻居之间通过3个链接相连。因此，该网络具有较高的聚团系数。实际上，如果所有4个邻居之间都存在链接，它们之间将有6条链接。由于邻居间实际上只有3个链接，所以聚团系数是3/6，即0.5，和我们在数学家合作网络中发现的0.56非常接近。为了说明这的确意味着明显的聚团现象，我们考察另一个随机网络——每个节点仍然有4个邻居，但却是和系统中任意节点随机连接的。那么，4个邻居之间的连接个数依赖于网络的大小。如果和图4-2中的网络一样有12个节点，随机网络的聚团系数就是0.33。然而，如果网络中有10亿个节点，聚团系数将下降到10亿分之4！很明显，此时新模型中的聚团系数还是0.5，是随机网络聚团系数的10亿倍。

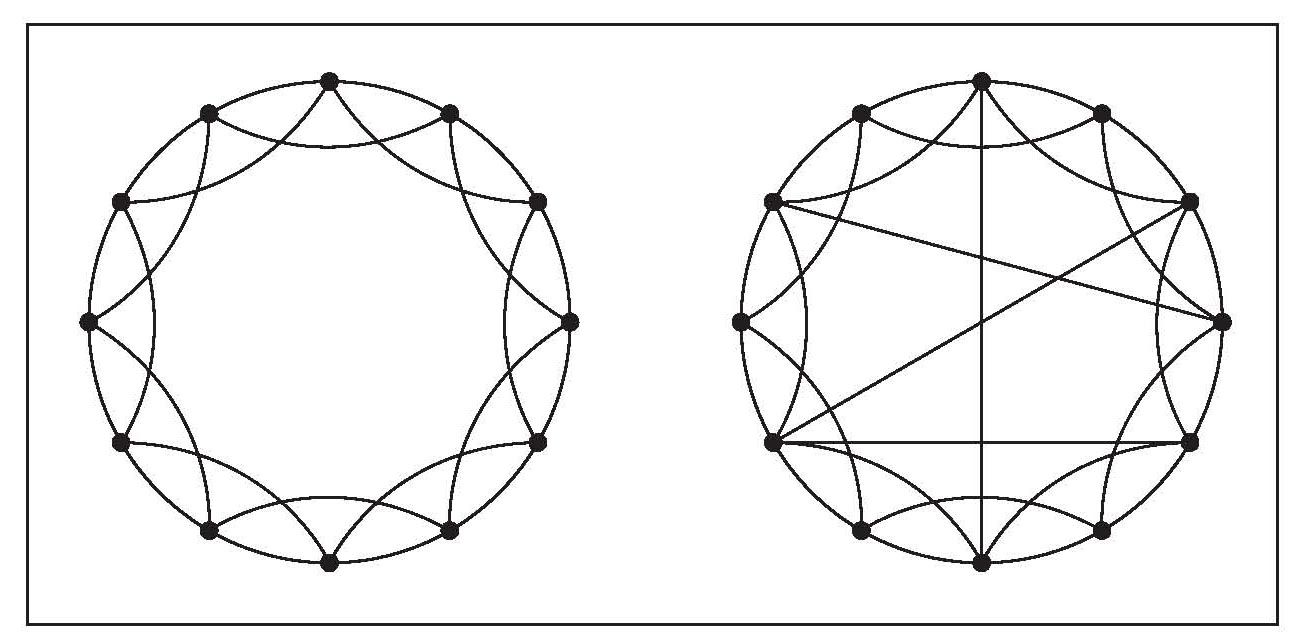
为了建模高度聚团的网络，邓肯·瓦茨和史蒂文·斯托加茨研究节点形成的圈，每个节点仅与它的直接邻居和相距两步的邻居相连接（左图）。为了让世界变得更小，添加了少量几个额外的链接，每个链接连接两个随机选择的节点（右图）。这些长程链接为距离较远的节点提供了关键的捷径，大大缩短了所有节点间的平均间隔。

图4-2 聚团化的小世界

不过，我们也要为新模型带来的高聚团性付出一些代价——在该模型中小世界不复存在。在图4-2所示的社会模型中，和我距离近的只有我的直接邻居和二度邻居。要想和圈子另一边的人取得联系，我得走遍半个圈子，沿途经过很多人的介绍。实际上，很容易就能确定，连接顶部节点和底部节点的最短路径至少要经过3个链接。这看起来并不多，但是，如果我们有足够的耐心和空间在同一个圈上画上60亿个节点，每个节点仅与直接邻居和二度邻居之间存在链接，那么，从一边到另一边的最短路径，要经过不止10亿条链接。因此，在这样一个圈子上构建的社会，不仅高度聚团，而且是一个大世界。

现实中，地球上相距遥远的人之间也存在着链接。每个人除了邻居之外，还有一些相距较远的朋友。

假如我想找出一条结识澳大利亚某个人的途径，我不会挨家挨户地寻找，如果那样做，我迟早会碰到太平洋而不能再前进。或许，我会想起我高中时最好的朋友前几年搬到了悉尼。因此，我只需要联系我的这位朋友，通过他在澳大利亚逐步建立起来的人际关系，就能找到我要找的目标。

一个能够真实反映当今社会的模型，一定允许远距离链接的存在。在前面描述的聚团模型中，我们很容易实现这一目标，只需要在一些随机选择的节点间添加少量的链接即可。也就是说，在圈子上任意选择两个节点，在它们之间添加一条新的链接。如此一来，被选中的两个节点间的距离便降到1，而它们的直接邻居之间的距离也大大缩短了。如果添加很多这样的随机链接，便能让所有节点间的距离都缩短。

链接洞察

瓦茨和斯托加茨指出了一个惊人的发现：即使只添加少量几个链接，也能大大降低节点间的平均间隔，而新添加的这些链接并没有显著改变聚团系数。然而，这些链接构成了长的桥梁，它们往往连接着分处圆圈两边的节点，于是，所有节点之间的间隔瞬间缩短。在瓦茨和斯托加茨的模型中，节点间的间隔大大缩短，而聚团系数基本保持不变。这表明，在选择朋友时，我们更倾向于选择身边的人，只有很少一部分人拥有长程链接。这个简单的模型告诉我们，六度分隔源于这样一个事实：有些人的朋友和亲戚不是他们的左邻右舍。这些远距离的链接，让世界上相距遥远的人之间有了捷径。大型网络的链接不再需要是完全随机的，便能展现出小世界特性，只要有少数几个随机链接就足够了。

抛弃随机世界观

埃尔德什去世两年后，瓦茨和斯托加茨发表了关于聚团性的论文，引起了物理学家和数学家的巨大兴趣。首先，这篇论文提出了一个具有显著聚团性的模型，为格兰诺维特的观点提供了形式化的解释。其次，这篇论文在将小世界问题带到物理和数学领域方面发挥着独特的作用，在此之前，小世界问题只是社会学研究的问题。短时间看来，瓦茨和斯托加茨提出的更通用的、可以建模聚团性的模型将会取代埃尔德什和莱利的随机宇宙。每个人都能联想到一个简单的场景：我们熟悉的局部有序中散落着一些远距离链接，为我们身边的小世界现象提供了清晰明了的解释。该模型是埃尔德什和莱利的完全随机世界和正则栅格的优美折中：完全随机世界是小世界，却排斥朋友圈；正规栅格虽然具有高的聚团性，节点之间却相距很远。

今天，我们认识到，瓦茨-斯托加茨模型和埃尔德什-莱利的世界观并不矛盾。通过假定我们从正则栅格开始，聚团的确存在。但是，从很多角度讲，该模型的根本原理和埃尔德什-莱利的观点是吻合的。譬如，除了最初将节点布置在一个圆圈上之外，我们连接节点的方式是完全随机的。因此，这两个模型都描述了一个高度平等的社会，链接是通过掷骰子来决定的。

1998年，瓦茨和斯托加茨的里程碑论文发表时，我的研究组正在尝试理解复杂网络的结构，主要关注的是万维网。我们花了很长时间才完全理解这篇论文透露的重要信息，并领悟到该模型能够将埃尔德什-莱利的世界观和格兰诺维特的聚团社会统一在一起。在最终理解了这篇论文时，我们手头有一件紧急的事情需要处理。我们的采集机器人得到的网络，完全不同于埃尔德什-莱利和瓦茨-斯托加茨的模型所预言的网络。我们在下一章将会看到，万维网中有很多枢纽节点，这些节点拥有异常多的链接。问题是，在埃尔德什和莱利的平等模型中，这样的枢纽节点非常罕见，因此，该模型显然不能解释机器人的这一发现。瓦茨-斯托加茨模型的表现同样糟糕：该模型同样抑制那些链接数比节点平均链接数多很多的节点的出现。这两个模型明显缺少了某些重要的东西，因此制约了我们对网状宇宙的理解。数据促使我们寻找对真实网络的更好理解，最终迫使我们完全放弃随机世界观。沿着这样的路径，事情发生了出人意料的转折。我们不得不放弃目前为止掌握的所有关于网络的认识。

[1] 完全图是每对顶点之间都恰连有一条边的简单图。——编者注