第6链 幂律——复杂网络的分布规律

40年前，埃尔德什和莱利将复杂网络放到“随机”灌木丛中，而幂律将复杂网络从中拉了出来，并将其放到色彩斑斓、内涵丰富的“自组织”舞台上。盯着微型搜索引擎带回来的幂律，我们在网络中看到了一种全新而未知的秩序，这种秩序具有不同寻常的优美和一致性。

幂律分布

幂律分布是一条没有峰，且不断递减的曲线，它最突出的特征是大量微小事件和少数非常重大的事件并存。假设某个星球上居民的身高遵循幂律分布，那么，大多数人都非常矮。但偶尔看到一个几百米高的巨人走在大街上，人们也不会觉得吃惊。

无尺度网络

无尺度网络是遵循幂律度分布的网络。网络中大多数节点只有很少几个链接，它们通过少数几个高度连接的枢纽节点连接在一起。在形状上，无尺度网络很像航空交通系统，很多小机场通过少数几个主要的交通枢纽连接在一起。

帕累托与80/20定律

维弗雷多·帕累托（Vilfredo Pareto）是一位非常有影响力的意大利经济学家。20世纪初，他在日内瓦的一个经济学会议上发言时，不断被他强势的同事古斯塔夫·冯·施穆勒（Gustav von Schmollez）打断。冯·施穆勒当时就职于柏林大学，是德国学术界的权威，他用盛气凌人的声调不断地喊着：“经济学里有定律吗？”

帕累托虽然出身贵族家庭，却不修边幅。据说，他在撰写不朽著作《普通社会学通论》（Trattato di Sociologia Generale）时，只有一双鞋子和一套西服。因此，第二天，他很容易就把自己扮成了一个乞丐，在大街上拦住了冯·施穆勒。“行行好吧，先生，”帕累托说道，“您能告诉我哪里能找到吃饭不花钱的饭店吗？”“可怜的伙计，”冯·施穆勒答道，“世上哪有这样的饭店呀？不过，街角有个地方，花不了多少钱就能吃上一顿不错的饭。”“哈，”帕累托得意洋洋地笑道，“看来经济学里是有定律的呀！”

在做了20年铁路工程师后，帕累托把精力转到了经济学。他深受牛顿物理学的数学之美的影响，将生命剩余的时间都投入到把经济学变成严谨科学的梦想之中，希望找到像艾萨克·牛顿的原理那样精确而通用的定律来刻画经济学。他孜孜不倦的追求带来三卷专论，成为后世经济学家和社会学家灵感和思想的不竭之源。

在学术之外，帕累托凭借一个经验观察而享有盛名。作为一个勤劳的园丁，他注意到，80%的豌豆是20%的豆荚结出的。作为经济不平等现象的细心观察者，他发现意大利80%的土地被20%的人口占有。最近，帕累托定律（也被称为80/20定律）又演变成管理学中的墨菲定律：80%的利润由20%的员工创造，80%的客户服务问题来自20%的顾客，80%的决定在20%的会议时间里完成，诸如此类。80/20法则还在很多领域里以常识的形式出现，例如，80%的犯罪行为来自20%的罪犯。

虽然有着各种各样的外在形式，80/20定律描述的其实是同一个现象：大多数情况下，我们五分之四的努力是无关紧要的。我们再贡献几条与80/20定律近似的说法：万维网上80%的链接仅指向15%的网页，80%的引用指向38%的科学家，好莱坞80%的链接连向30%的演员。这似乎是在诱人推断，80/20定律适用于任何情形，但这其实是夸大其词。现实中，遵循帕累托定律的所有系统都有些特别之处。它们的特别之处源自一个性质，该性质对于理解复杂网络同样发挥着关键作用。

幂律分布与度指数

当郑浩雄开始设计万维网采集机器人时，对万维网背后的网络到底是什么样子，我们只有一些极其简单的预期。受埃尔德什和莱利观点的指引，我们希望看到，网页之间是随机连接的。像我们在第2链中讨论的那样，一个网页的链接数遵循着单峰分布，这说明，大多数文档的流行度都差不多。但是，机器人带回的网络中，很多节点仅拥有少量链接，一些枢纽节点却拥有非常多的链接。当我们尝试在双对数坐标系下拟合节点连接度的直方图时，最奇怪的事出现了。拟合结果表明，网页链接数的分布严格遵循被称为幂律的数学表达式。

如果你不是物理学家或数学家，你可能从没有听说过“幂律”。这是因为，自然界中大多数的量都遵循钟形曲线，而钟形曲线对应的分布和刻画随机网络的单峰分布非常相似。例如，测量一下你认识的所有成年男性的身高，数一数他们中多少人的身高是1.2米、1.5米、1.8米或者2.1米，进而画出一个直方图。你会发现，大多数人的身高都介于1.5米和1.8米之间。直方图在这些值附近有一个峰。实际上，除非你认识很多篮球运动员，否则，你的朋友中只有很少人高达2.1米，甚至2.4米。身高矮的人也一样：身高0.9米和1.2米的人非常罕见。自然界中大多数的量遵循这样的单峰分布，包括人类的智商和大气分子的速率，因此，很多人对这些普遍存在的钟形曲线非常熟悉。

在过去几十年里，科学家发现，自然界有时会产生一些遵循幂律分布的量，它们不再遵循钟形曲线。幂律和描述我们身高的钟形曲线有很大差异。幂律分布没有峰，遵循幂律分布的直方图是不断递减的曲线，这意味着，很多小事件和一些大事件并存。假设某个星球上居民的身高遵循幂律分布，大多数人都非常矮。然而，偶尔看到一个几百米高的巨人走在大街上，人们也不会觉得吃惊。实际上，如果那个星球上有60亿人，至少有一个人的身高会超过8000米。因此，幂律最突出的特征不是有很多小事件，而是大量微小事件和少数非常重大的事件并存。但这些非常重大的事件绝对不可能出现在钟形曲线中。^[1]

每一个幂律都有一个独一无二的幂指数。通过幂指数我们可以得知，相对于那些不流行的网页，到底有多少非常流行的网页。在网络中，幂律可用于描述度的分布，而幂指数通常被称为度指数。我们的测量表明，网页的导入链接数的分布遵循幂律，度指数接近2。导出链接也遵循类似的幂律分布，不过它的度指数稍微大一些。^[2]

我们的微型机器人给出了令人信服的证据：数百万网页创造者以某种神秘的方式协同工作，形成了复杂的万维网，在这里，随机宇宙不再存在。它们的集体行动让度分布避开了钟形曲线——随机网络的标志，并将万维网变成了一个由幂律描述的奇特网络。但是，机器人不能回答我们最迫切想要知道的问题：到底是什么促使万维网偏离了随机网络的严格预言呢？

后来我们认识到，可以从另外一个途径来回答该问题。大多数复杂网络是不是都可以用一些简单的定律来刻画呢？而我们之所以还没有看到这些定律，是因为我们之前没有去探索。这个新的提问带来了丰硕的成果。实际上，几个月后，在分析好莱坞演员网络时，我们发现它也遵循同样的数学关系：恰好认识k个其他演员的演员数目按照幂律的方式衰减。随后，我们得知埃尔德什和他的数学家同事也遵循这样的定律。细胞内部的网络也遵循该定律，和k个其他分子有交互的分子数目按照幂律的方式衰减。同时，我们发现了波士顿大学物理教授希德·雷德纳（Sid Redner）的一篇论文，他在论文中指出，物理期刊引用数的分布遵循幂律。把出版物视为节点，把引用视为链接，雷德纳的发现意味着，这样的引用网络也可以用幂律度分布来描述。随后，在我们和其他科学家有机会研究的很多大网络中，出现了令人吃惊的简单一致的模式：恰好拥有k个链接的节点数遵循幂律，每个系统的度指数不同，大多介于2和3之间。

不均匀性，幂律度分布网络的特性

随机网络和幂律度分布描述的网络之间最突出的视觉和结构差异，可以通过对比美国的公路图和航空线路图清晰地看出。在公路图中，城市是节点，城市间的高速公路是链接。这是一个非常均匀的网络：每个主要城市至少有一条高速公路，没有哪个城市拥有几百条高速公路。因此，大多数节点非常相似，拥有差不多的链接数。正如我们在第2链看到的，这种均匀性是拥有单峰度分布的随机网络所固有的性质。

航空线路图和公路图有着极大的不同。航空线路图对应的网络中，节点是机场，链接是机场间的直飞航班。在每个飞机座椅后背都放有飞行杂志，杂志封面上印有航空路线图，只需看上一眼，你一定不会错过那少数几个枢纽节点，例如，芝加哥，达拉斯，丹佛，亚特兰大和纽约，从这些枢纽节点出发，有通往其他所有美国机场的航班。绝大多数机场都很小，最多只有几个链接把它们和一个或几个枢纽节点连接起来。因此，和大多数节点都差不多的高速公路图相比，航空路线图中少数几个枢纽节点连接着数百个小机场（见图6-1）。

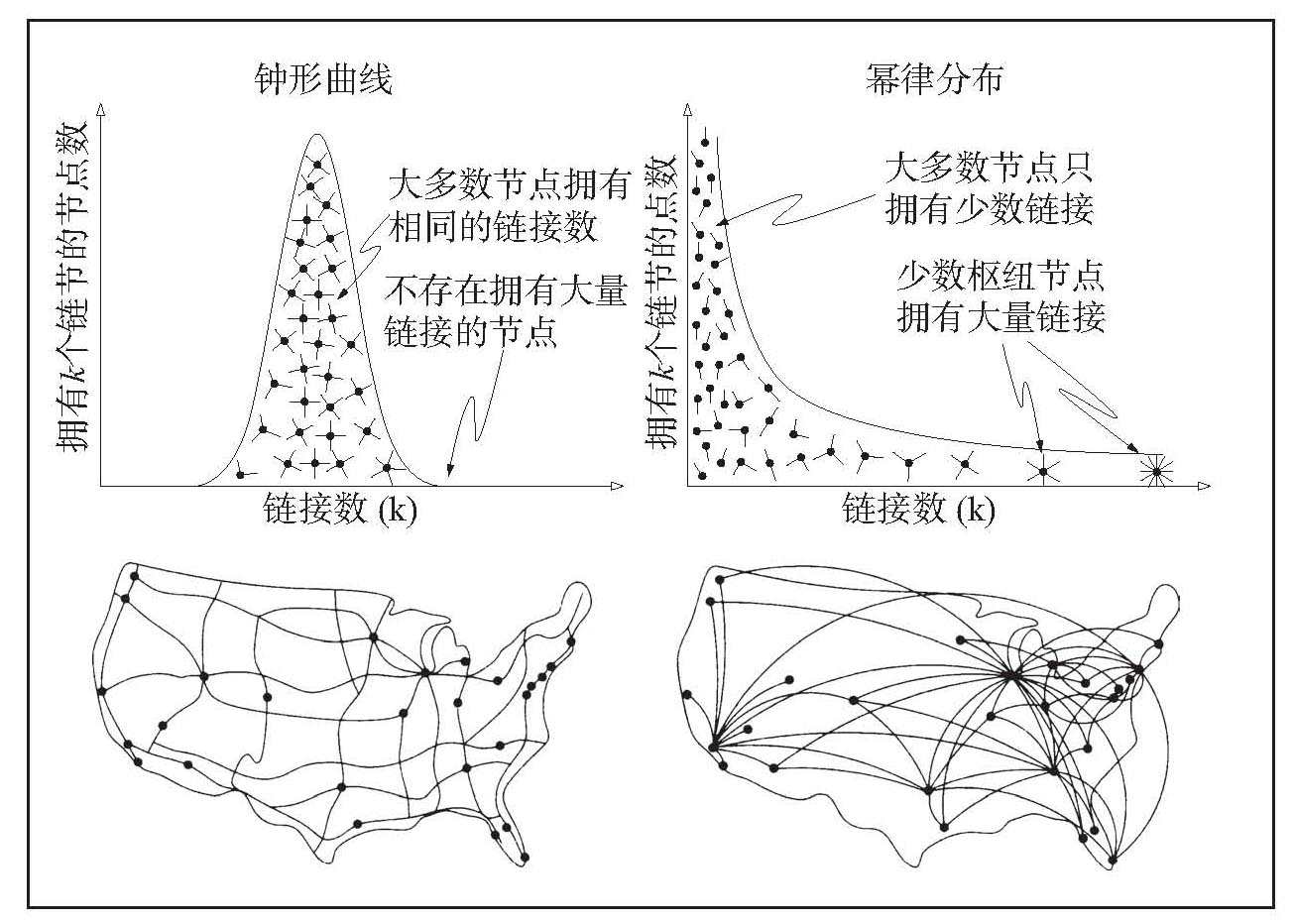
随机网络的度分布遵循钟形曲线，这表明，大多数节点拥有相同的链接数，不存在拥有非常多链接的节点（左上图）。因此，随机网络和国家高速公路网络类似，公路网络中，节点是城市，链接是城市间的主要高速公路。实际上，大多数城市的高速公路数相差无几（左下图）。相比而言，无尺度网络的幂律度分布表明，大多数节点只拥有少数几个链接，它们通过少数几个拥有大量链接的枢纽节点连接在一起（右上图）。视觉上看，无尺度网络很像航空交通系统，很多小机场通过少数几个主要的交通枢纽连接在一起（右下图）。

图6-1 随机网络和无尺度网络

这种不均匀特性是拥有幂律度分布的网络所具有的特性。幂律从数学上阐释了这样一个事实：在大多数真实网络中，绝大多数节点仅有少数几个链接，而这些数量众多的小节点和为数不多的大枢纽节点并存，每个枢纽节点拥有非常多的链接。小节点拥有的少数链接如果连向其他小节点，便不足以保证网络是完全连通的。网络的连通性由少数枢纽节点保证，是它们让真实网络免于瓦解。

在随机网络中，分布的峰意味着绝大多数节点拥有同样数目的链接，链接数偏离平均数的节点极其罕见。因此，随机网络的节点连接度具有特征尺度，该特征尺度由平均节点体现，并由度分布的峰确定。相比而言，幂律度分布没有峰，这意味着，真实网络没有诸如特征节点这样的现象。我们看到的是节点间连续的层级结构，从少数枢纽节点到为数众多的小节点。最大的枢纽节点之后紧跟着两三个稍微小一些的枢纽节点，随后是十几个更小的节点，最后是为数众多的小节点。

链接洞察

幂律分布迫使我们放弃了尺度或者特征节点的想法。在连续的层级中，无法找到一个能够代表所有节点特性的节点。在这些网络中不存在固有的尺度。这就是我的研究组把拥有幂律度分布的网络称为“无尺度”的原因。在意识到自然界大多数复杂网络符合幂律度分布之后，“无尺度网络”一词迅速渗透到和复杂网络相关的大多数学科中。

1999年，我们发现了无处不在的枢纽节点间的等级差别以及随之而来的幂律。然而，当时已有的两种网络理论都不能解释我们发现的现象。人们把这些现象的出现视为偶然。埃尔德什和莱利的随机网络理论以及瓦茨和斯托加茨对其进行扩展后容忍聚团的理论，都认为具有k个链接的节点数目应该指数衰减，这要比幂律所预测的衰减快得多。这两种网络理论通过严格的数学论证告诉我们，枢纽节点不会存在。

在万维网中发现了幂律是一件令人吃惊的事情，这迫使我们承认枢纽节点的存在。衰减慢的幂律分布以一种自然的方式容忍这些高度连接的异常节点的存在。幂律分布预言，每个无尺度网络中都有一些大的枢纽节点，是它们从根本上确定着网络的拓扑。人们发现，包括万维网和细胞网络在内的大多数重要网络都是无尺度的，这让人们逐步认可了枢纽节点的存在。我们将看到，枢纽节点决定着真实网络的结构稳定性、动态行为、健壮性、容错性和故障容忍性。它们的存在预示着，有一些非常重要的组织规则在支配着网络的演化。

幂律，复杂网络背后的规律

帕累托从未使用过80/20的说法。这个说法是后来研究帕累托所观察现象的经济学家们提出的。19世纪末，帕累托注意到，自然界和经济中有一些量不服从无处不在的钟形曲线，而是遵循幂律分布。例如，少数几个非常富有的人挣了大多数的钱，而绝大多数人都挣得非常少。帕累托的发现意味着，差不多80%的钱被仅占总人口20%的人挣去了。这种收入不均衡现象，在被帕累托发现一百年后，仍然伴随着我们。

80/20一词究竟是何时出现的，人们并不清楚。在物理学家和数学家大谈幂律时，80/20定律风行于大众媒体和商业刊物中。但是，只要80/20定律适用，你就可以确定，其背后一定有幂律存在。幂律从数学角度阐释了这样的概念：少数几个大事件发挥了大部分的作用。

在完全随机的系统中，幂律极少出现。物理学家已经明白，幂律通常标志着从无序到有序的过渡。因此，我们在万维网中看到的幂律，首次以严格的数学术语表明，真实网络远不是随机的。最终，复杂网络开始用只有研究自组织和复杂性的科学家们才能理解的语言和我们对话。复杂网络诉说着有序和涌现行为，而我们只需要仔细聆听。

网络遵循简单的幂律，这一发现似乎只能让少数数学家和物理学家感到兴奋不已。但是，幂律处于20世纪后半段某些最惊人理论进展的核心位置，出现在混沌、分形、相变等领域中。在网络中观察到幂律，预示着网络和其他自然现象之间存在着未知的联系，从而将网络置于理解一般复杂系统的最前沿。万维网、好莱坞、科学家、细胞和很多其他复杂系统背后的网络都遵循幂律，这一事实让我们可以对帕累托的观点进行升华，首次提出“复杂网络背后或许存在定律”。

自发涌现

水分子符号H₂O看上去很像米老鼠，大大的O是头，两个H是耳朵。对于水分子，无论是其大小还是内部结构，我们都已经了解得非常清楚。这一点都不奇怪，毕竟水是地球上最常见和被研究最多的物质。但是，玻璃杯里由数十亿紧密结合的水分子形成的液态水，对我们而言仍是个挑战。

气体很简单：分子在空荡的空间里飞行着，两个分子只有彼此碰到一起时才会注意到对方的存在。晶体虽然相反，却同样简单：分子手拉手，紧密结合在一起，构成非常完美的晶格。液体则在这两个极端状态间达成了一种微妙的平衡。让水分子保持在一起的吸引力不足以迫使它们形成严格的秩序。在有序和混沌之间，水分子跳出了一曲奇妙的舞蹈，一些分子走到一起，形成有序的小组，一起移动，很快又彼此分开，和其他分子一起形成新的小组。

对一杯水进行冷却，并不能让水分子的壮观舞蹈发生显著变化，只能使分子的运动变得更庄严——步伐沉重而缓慢。然而，温度到达0℃时，奇妙的事情发生了。水分子突然形成了完全有序的冰晶体，就像是四处走动的士兵听到了长官的命令开始整装列队一般。不过，士兵们经历了数百次的操练，早就掌握了自己在队列中的确切位置。相比之下，这些水分子之前可能从没有结成过冰。某种神秘的力量推动它们从四处游走的状态切换到严格有序的状态。作为寒冷和完全秩序的象征，我们熟悉的冰就这样自发涌现出来了。

水变成冰是相变现象最著名的例子之一。19世纪60年代之前的几十年里，物理学家一直在努力理解相变现象。在很多物质中都有相变现象，其形式可能和水结冰有着很大的不同。例如，磁化金属中的每个原子都有一个磁矩或自旋，通常用穿过原子的小箭头来表示。在高温状态下，原子的自旋随机地指向不同的方向。然而，当冷却到某个临界温度时，所有原子的自旋将指向同一个方向，从而形成磁体。

液体结冰和磁体涌现都是从无序到有序的相变。实际上，和冰的完全有序相比，液体水是无组织的。在凝固点，这种无序状态奇迹般地消失了，取而代之的是一种高度对称和有序的状态。类似地，磁化金属中随机指向的自旋处于一种无序状态。可一旦冷却到临界温度，这些自旋就非常有序地指向同样的方向。这种突然转变蕴含着理解自然界奥秘的钥匙，科学家和哲学家都对此抱有极大的兴趣：有序是如何从无序中涌现出来的？

有序如何从无序中涌现

磁体的有序和无序状态对应着物质不同的热力学状态。在相变点，系统在两个状态间面临的抉择，就像站在山脊上的登山者要选择从哪一边下山一样。在没有做出决定之前，系统通常左右摇摆，这种摇摆在临界点附近达到极致。

这种摇摆带来的结果可以通过实验测量。在临界点，有序的因素和无序的因素交织在同一种物质中，意味着系统可以向两个方向探索前进。在接近相变温度的金属中，自旋指向同一方向的原子开始形成簇。金属越接近临界点，预示着有序磁体的原子簇变得越大。19世纪60年代，物理学收集了越来越多的实验证据，证据表明，在接近临界点时，一些关键的量遵循幂律。例如，原子间彼此通信的距离，即“关联长度”，经常被当作原子簇大小的粗略度量。测量结果表明，在接近临界点时，关联长度按照幂律的方式增加，该幂律具有独特的临界指数。金属离相变温度越近，自旋之间的距离越大。临界温度附近，金属的磁性强度由指向同一方向的自旋所占的比例决定，磁性强度也遵循幂律，只是临界指数不同。

随着物理学家仔细研究不同的系统中有序是如何从无序中涌现出来的，越来越多的幂律在相变过程中被发现。无论是液体加热后变成气体，还是铅在足够低的温度下变成超导体，物理学家从中都发现了幂律。这种从无序到有序的相变开始展现出令人惊奇的数学一致性。但问题是，没有人知道这背后的原因。为什么液体、磁体和超导体在一些临界点不见了，开始遵循相同的幂律呢？这些不同的系统之间的高度相似背后隐藏着什么呢？幂律到底和什么相关呢？

从“随机”灌木丛到“自组织”舞台

1965年的圣诞周，人们在理解无序到有序的相变方面取得了第一个重大突破。厄巴纳（Urbana）的伊利诺伊大学的物理学家利奥·卡达诺夫（Leo Kadanoff）突然悟到：在临界点附近，我们不能再把各个原子分开研究。相反，这些原子应该被视为行动一致的群体。原子被由原子形成的盒子取代，每个盒子中的原子行为一致。

那时候，最优秀和最聪明的理论物理学家已经花费了大量的时间研究相变，发现了9个不同的临界指数，每个临界指数和临界点附近涌现出的某个幂律相关。卡达诺夫的想法提供了引人注目的可视化模型，能够用于推导出众多临界指数间精确的数学关系。他证明了，从无序到有序的相变不需要所有9个未知的指数，而是可以使用它们中的任意两个来表达。当时他并不知道，其他一些研究人员在同一时间得出了同样的结论。来自康奈尔大学的物理化学家本·维多姆（Ben Widom）以及来自前苏联的物理学家A.Z.巴达辛斯基（A.Z.Patashinskii）和V.L.波克洛夫斯基（V.L.Pokroskii），都采用不同的方法推导出了相似的尺度关系。康奈尔大学的物理学家迈克尔·费舍尔（Michael Fisher）推导出了临界指数间的一组不等式，为这些幂指数的秩序提供了进一步的线索。

然而，还缺少一些东西。还没有理论能够找出剩余的两个指数，也没有理论能够解释为什么每当复杂系统自发涌现出秩序时总会出现幂律，人们甚至根本不清楚这样包罗万象的理论是否存在。鉴于目前得到的结果优美且统一，每个人都希望这一理论是存在的。物理学界一直等到1971年11月才找到最终的答案。出人意料的是，答案来自一位没有涉足过相变和临界现象的物理学家。

20世纪60年代后期，肯尼斯·威尔逊（Kenneth Wilson）是康奈尔大学物理系一位毁誉参半的助理教授。每个人都知道他很聪明，但是他的聪明才智没能变成学术著作——这是学术界量化成功的有形指标。这些问题险些影响到他在康奈尔大学的教职。迫于终身教职委员会的压力，他从抽屉里抽出几份稿件发表了。其中两份稿件在1971年6月2日同时投稿，并在这一年11月发表在《物理学评论B》（Physical Review B）上，它们改变了统计物理学。这两份稿件为相变提供了一个优美而统一的理论。

威尔逊发展了卡达诺夫提出的尺度想法，并将其变成一种强大的理论，称为“重整化”。他研究方法的出发点是尺度不变性：假定在临界点附近，物理定律在所有尺度上以相同的方式适用，尺度从单个原子变化为包含数百万行为一致原子的盒子。通过给出尺度不变形的严格数学基础，每当接近从无序到有序的临界点时，威尔逊的理论总能推导出幂律。威尔逊的重整化理论不仅解释了幂律，而且首次预测出那两个缺失的临界指数的值。他给相变金字塔添上了最后一块石头，这一成就让他赢得了1982年的诺贝尔物理学奖。

链接洞察

自然界往往厌恶幂律。在常见的系统中，量遵循钟形曲线，而且相关性按照指数率迅速衰减。但是，当系统被迫发生相变时，所有这一切都改变了。于是，幂律出现了——这是自然界给出的明白无误的迹象，表明混沌正在让位于有序。相变理论清清楚楚地告诉我们，从无序到有序的道路，是自组织在强有力地推动，并通过幂律铺就。它还告诉我们，幂律不仅是刻画系统行为的另一种方式，更是复杂系统自组织所独有的特性。

幂律所具有的这种独特而深远的意义，或许解释了我们在万维网中观测到幂律时如此兴奋的原因：不仅因为幂律在网络中是前所未有和出人意料的，更是因为，40年前，埃尔德什和莱利将复杂网络放到“随机”灌木丛中，而幂律将复杂网络从中拉了出来，并将其放到色彩斑斓、内涵丰富的“自组织”舞台上。盯着微型搜索引擎带回来的幂律，我们在网络中看到了一种全新而未知的秩序，这种秩序具有不同寻常的优美和一致性。

幂律无处不在

20世纪60年代后期和70年代初期，尺度和重整化理论提出时，试图理解磁体如何工作和水为什么凝固的物理学家们得到了启示。他们意识到，接近临界点时，有序从无序中涌现出来，此时，所有对此感兴趣的量遵循着由临界指数刻画的幂律分布。但是，无论是水从液体变成气体，岩浆凝固成岩石，金属变成磁体，还是陶瓷变成超导体，同样的定律总是适用，形成神奇的幂律。我们最终知道了，在秩序形成时，复杂系统剥去了各自独有的特性，展现出很多系统都具有的普遍行为。

在经历从无序到有序的相变的系统中，幂律无处不在。我的博士生导师尤金·斯坦利开玩笑说，在波士顿只有与双对数有关的论文。当时，斯坦利在波士顿大学带领一个活跃于相变研究方面的研究组，他参与了塑造我们对相变和普遍性理解的所有重要发现。他这里所指的双对数是科学家们从实验数据中发现幂律时常用的坐标系。实际上，在20世纪80年代和90年代，在物理学家、生物学家、生态学家、材料科学家、数学家和经济学家看到自组织存在的地方，就有幂律和普遍性出现。如此看来，似乎所有的网络都没有什么区别：枢纽节点背后有着非常严格的数学表达式——幂律。

这将我们带到了另一个难题面前。如果幂律代表着系统正从混沌向有序转变，那么，复杂网络中正在发生的是什么类型的转变呢？如果幂律出现在临界点附近，又是什么让真实网络处于临界点并让它们展现出无尺度行为呢？在物理学家揭示了支配相变的机制之后，我们才开始理解相变现象。现在，严格的理论使我们能够准确地计算出用于刻画正在形成序的系统的所有量。然而，在网络中，我们只是观测到了枢纽节点。我们现在知道枢纽节点是幂律的结果，而幂律是自组织和有序的标志。因此，这是一个重要的突破，我们可以把网络从随机的王国中拉出来。但是，产生枢纽节点和幂律分布的机制是什么，这个最重要的问题还没有得到解答。真实网络是处于从无序到有序转变的连续状态中吗？为什么枢纽节点出现在包括演员网络和万维网在内的各种网络中呢？为什么枢纽节点用幂律来描述？是否存在某种根本定律让不同的网络具有相同的普遍形式和形状？自然界是如何织成这些网络的呢？

[1] 请注意，幂律分布和钟形分布在分布的尾部存在着重要的定性差异。钟形分布的尾部指数衰减，衰减速度比幂律分布快很多。指数衰减的尾部造成枢纽节点不存在。相比而言，幂律分布衰减得慢很多，允许像枢纽节点这样的“罕见事件”存在。

[2] 这意味着，有k个导入链接的网页数目N（k）遵循公式N（k）～k^-γ，这里的参数^γ是度指数。在双对数坐标下，直线的斜率表示度指数。这里，度指数的值接近2.1。在计算某个给定网页的导出链接时，我们观察到了同样的模式：双对数坐标下的图表明，有k个导出链接的网页数遵循公式N（k）～k^-γ，这里γ=2.5。