第7链 富者愈富——复杂网络的先发优势

在我们不得不引入生长机制之前，经典模型的静态特性一直没有人注意；在幂律要求我们引入偏好连接之前，随机性也不是什么问题。结构和网络演化不能彼此分开，认识到这一点之后，我们很难再回到主宰我们思维方式几十年之久的静态模型。这种思维方式的转变缔造了一组反义词：静态和生长，随机和无尺度，结构和演化。

无尺度模型

真实网络由两个定律支配着：生长机制和偏好连接。每个网络都是从一个小的核开始，通过添加新的节点而增长。然后，这些新节点在决定连向哪里时，会倾向选择那些拥有更多链接的节点。无尺度模型将生长机制和偏好连接结合在一起，首次解释了真实网络中观测到的无尺度幂律。

幂律为什么会出现

波尔图曾经是葡萄牙帝国重要的商业港口，如今却只是一座被遗忘的城市。水流舒缓的杜罗河穿过海岸边陡峭的山谷，一路前行，在这里汇入大西洋。中世纪时，波尔图贸易繁荣，战略地位险要，易守难攻。宏伟的城堡临杜罗河（Duoro）而建，这里的葡萄酒酿造历史悠久，人们可能认为，波尔图是世界上游人最向往的地方之一。但实际上，这座城市地偏一隅，藏身在伊比利亚半岛的西北角，很少有游客会绕道到此。而且，真正对浓郁的波尔图葡萄酒感兴趣的人太少了，无法将这座伟大的中世纪古城从睡梦中唤醒。

1999年夏，我来到了波尔图。当时，我和学生一起刚刚完成万维网中幂律作用的论文初稿。我到这里是为了参加关于非均衡和动态系统的一个研讨会，该研讨会的组织者是波尔图大学的两位物理学教授，何塞·门德斯（José Mendes）和玛利亚·桑托斯（Maria Santos）。在1999年的夏天，研究网络的人还非常少，研讨会上没有一个报告是和网络相关的。然而，我当时满脑子都是网络。我不禁走神了，脑海里一直在思索我们尚未解答的几个问题：为什么会有枢纽节点呢？为什么会出现幂律呢？

那时候，万维网是唯一一个在数学上证明存在枢纽节点的网络。为了理解万维网，我们努力探索它独有的特征。同时，我们还想了解更多网络的结构。因此，就在我去波尔图之前，我联系了邓肯·瓦茨，他非常友好地为我们提供了描述美国西部电网和线虫拓扑的数据。设计“贝肯神谕”网站的研究生布雷特·加登现在是俄亥俄大学计算机科学系的助理教授，他将好莱坞演员数据库发给了我们。圣母大学计算机科学系的教授杰伊·布罗克曼（Jay Brockman）为我们提供了一个人工网络的数据——IBM制造的电脑芯片的布线图。在我去欧洲前，我的研究生雷卡·阿尔伯特和我商讨后决定由她来分析这些网络。6月14日，离开一周后，我收到她发来的一封很长的电子邮件，邮件详细介绍了她的研究进展。在邮件的末尾，她写了这样一句总结语：“我检查了所有的度分布，在几乎所有的系统（IBM的芯片，演员，电网）中，分布的尾部都遵循幂律。”

雷卡的邮件无疑表明，万维网绝不是特例。坐在会议室里，我发现自己不再关注任何报告，而是一直在思考这一新发现的意义。如果万维网和好莱坞演艺圈这两个截然不同的网络都展现出幂律分布，那么，很可能是某些普遍规律或机理在发挥作用。如果这样的定律存在，它将适用于所有网络。

报告间的首个休息时间到了，我决定回到下榻的神学院静下心来思考一下。但是，我没有走太远。在走回房间的15分钟内，我想到了一个可能的解释，它非常简单直接，以至于我都怀疑它是否正确。我立即回到学校发传真给雷卡，让她用电脑验证一下我的想法。让我非常惊讶的是这个想法居然可行。这个简单的富者愈富的现象，可能出现在大多数网络中，它能够解释我们在万维网和好莱坞演员网络中观测到幂律的原因。

从波尔图回去后，我只能在圣母大学短暂停留，就又要外出一个月。不过，我肯定不能等一个月之后再提交我们的结果。所以，我只有7天的时间来写这篇论文。从里斯本到纽约需要飞行8小时，这似乎是准备初稿的绝佳时间。飞机一起飞，我就拿出去波尔图之前刚买的笔记本电脑，迅速开始写作。在我即将写完引言时，飞机服务员将一杯可口可乐递给我身边的乘客时，突然将它打翻在我的键盘上。瞬间，我的笔记本电脑屏幕上的字符开始闪烁，电脑报废了。然而，我最终还是在飞机上完成了论文初稿，只不过从头到尾都是手写的。一周后，我们将论文投给权威期刊《科学》。10天后，论文未经正常的同行评审就被拒掉了，因为主编认为论文没有达到该期刊要求稿件观点新颖和广受关注的标准。那时候，我已经到了位于喀尔巴阡山腹地的特兰西瓦尼亚，和家人朋友在一起。我很失望，但坚信这篇论文很重要。于是，我做了一件我以前从未做过的事：我给拒掉我稿件的主编打了电话，努力说服他改变决定。出人意料的是我竟然成功了。

放弃随机世界观的两个假设

埃尔德什和莱利的随机模型依赖两个简单且经常被忽视的假设。首先，我们从一组节点开始。所有这些节点从一开始就存在，这意味着，我们假设节点数目是确定的，并且在网络的生命期内保持不变。其次，所有节点是相同的。由于无法区分各个节点，我们随机连接它们。在网络研究的过去四十多年里，无人质疑这些假设。但是，枢纽节点的发现以及描述枢纽节点的幂律，迫使我们放弃了这两个假设。我们投到《科学》的稿件沿着这条路线迈出了第一步。

生长机制，先发先至

关于万维网，有一点大家都认同：它在不断生长。每天都有新文档添加到万维网中：

有些是个人讲述其爱好或兴趣的；

有些是公司推广在线产品和服务的；

有些是政府向市民发布信息的；

有些是大学教授公开课件讲义的；

有些是非营利机构向公众介绍其服务的；

有些是电子商务公司为了盈利而设计的。

据估计，万维网上的信息量在十年后将达到10¹⁸字节，这些信息会以多种格式在全球传播，大多数格式现在可能还没有出现。当人类收集的大多数信息都放到网上时，万维网上信息爆炸的速率可能会减缓，但是目前还没有减速的迹象。

目前，万维网上有超过10亿个文档，让人难以相信万维网是逐个节点出现的。但实际情况确实如此。仅仅10年前，万维网中还只有一个节点，这就是蒂姆·伯纳斯·李著名的首个网页。随着物理学家和计算机科学家开始创建自己的网页，早期的网站逐渐收到指向它们的链接。最初只有十几个文档的小规模万维网，是现在这个遍布全球、自组装起来的万维网的前身。虽然现在的万维网维度巨大且非常复杂，但它仍在逐个节点持续不断地生长。这种生长机制和前文所述网络模型的假设截然不同。那些模型都假设网络中的节点数目恒定不变。

好莱坞网络起初也只是一个很小的核，这个核是19世纪90年代第一批无声电影演员。根据IMDb.com数据库的资料，在1900年时，好莱坞只有53个演员。随着电影需求的增加，这个核开始慢慢扩张，每部电影都会带来几个新面孔。1908-1914年，好莱坞经历了第一次繁荣期，每年签约的演员数目从不到50增加到接近2000。第二次令人瞩目的繁荣期开始于20世纪80年代，电影制作变成了今天人们熟知的巨型娱乐产业。好莱坞网络从无声电影演员组成的很小的核，成长为一个拥有超过50万节点的巨型网络，并且仍在以惊人的速度持续增长。仅1998年一年，就有多达13209个演员首次出现在电影屏幕上，从而进入到IMDb.com数据库中。

链接洞察

尽管种类多样，但大多数真实网络具有共同的基本特征：生长机制。随意选择一个你能想到的网络，下面的情形很可能就是正确的：从少数几个节点开始，通过添加新的节点，网络增量式生长，逐渐到达现在的规模。很明显，生长迫使我们重新思考模型的假设。埃尔德什-莱利模型和瓦茨-斯托加茨模型都假设我们拥有固定数目的节点，然后将这些节点以某种巧妙的方式连接在一起。因此，这些模型生成的网络是静态的，也就是说，节点数目在网络生命期内保持不变。相比之下，我们的例子表明，对于真实网络而言，这个静态假设是不合适的。相反，我们应该将生长机制整合到网络模型中。这是我们在试图解释枢纽节点时得到的最初见解。如此一来，我们就颠覆了随机宇宙的第一个根本假设——静态特性。

建模生长网络相对容易。我们可以从一个小的核开始，一个接一个不断地添加节点。不妨假设每个新节点拥有两个链接。因此，如果最初有两个节点，第三个节点和两个节点都要相连。而第四个节点则有三个节点可供选择。我们选择哪两个节点进行连接呢？为了简单起见，我们按照埃尔德什和莱利的指引，从三个节点中随机选择两个，让新节点和它们连接。我们可以无限次地重复这个过程，每添加一个新节点，我们就让它和两个随机选择的节点进行连接。这个简单算法生成的网络为模型A，它与埃尔德什和莱利的随机网络模型的差异只在于它的生长特性。然而，这个差异非常显著。尽管我们仍然随机和平等地选择链接，但是模型A中的节点不再相同。很容易就能识别出其中的胜者和败者。在每个时刻，所有节点有同样的机会被连接，结果导致那些先加入的节点拥有明显的优势。事实上，除了极少的统计扰动之外，模型A中最早加入的节点将是最富有的，因为这样的节点拥有最长的时间来收集链接。最贫穷的节点则是最后加入到系统中的那个，由于还没有其他节点来得及去连接它，所以它只有两个链接。模型A是我们为解释在万维网和好莱坞网络中观测到的幂律而做出的最早尝试之一。计算机模拟结果很快证实，我们还没有找到答案。作为区分无尺度网络和随机模型的函数，模型A的度分布按照指数衰减得很快。早期加入的节点是明显的胜者，但是，指数形式的度分布表明，这种节点的度太小，数目也太小。因此，模型A不能解释枢纽节点和连接者。这表明，仅有生长机制还不能解释幂律的出现。

偏好连接，让强者愈强

1999年的“超级碗”期间，OurBeginning.com、WebEx.com和Epidemic Marketing等大量不知名的公司，为了能够让公司名字被数百万美国人知晓，将丹佛和圣路易斯比赛的每个广告位的价格炒到了200万美元。仅一年内，E*Trade就花费了3亿美元来提升公司的知名度。最流行的搜索引擎之一，AltaVista的广告预算接近1亿美元。在线公司中的巨头美国在线也迅速跟上，其广告费用为7500万美元。1999年，在线广告方面的花费超过32亿美元，几乎是同时期有限电视广告总值的一半，而有线电视是已经有着20年历史的媒体了。

这些公司到底想从中得到什么呢？答案不同寻常却简单。无论是创业公司，还是知名公司，都在将融到的风险投资和辛苦挣来的现金大量花费在广告上，每天支出数百万，目的就是在对抗埃尔德什和莱利的随机宇宙。他们想通过让其他人将链接指向它们，获得非随机性带来的优势。

在万维网中，人们究竟是如何选择网站进行连接的呢？按照随机网络模型，人们是随机地连接任意节点。然而，做选择的真实情形却并非如此。例如，很多网页选择将链接指向新闻门户网站。在Google上搜索“news”一词会返回大约109000000个搜索结果。雅虎手工编纂的分类目录中，在线报纸的数目超过8000个。那我们如何选择呢？随机网络模型告诉我们，可以从列表中随机选择。坦率地讲，我不认为有人这么做过。相反，大多数人只熟悉几个主要的新闻门户网站。当我们想浏览新闻时，会不假思索地从中选择一个。作为《纽约时报》的老读者，我无须多想就会选择nytimes.com。其他人可能更喜欢CNN.com或者MSNBC.com。然而，需要注意的是，我们倾向于连接的网页都不是普通的节点，而是枢纽节点。它们越出名，指向它们的链接就越多。它们吸引到的链接越多，人们就越容易在万维网中找到它们，因此会对它们更加熟悉。最终，我们在不知不觉中遵循着某种偏见，以较高的概率去连接自己知道的节点，这些节点是万维网中链接数较多的节点。所以，我们更喜欢枢纽节点。

上述现象的本质是，在万维网上决定连向哪里时，我们遵循着“偏好连接”：如果有两个网页可供选择，其中一个网页的链接数是另一个网页的两倍，那么选择链接数较多那个网页的人数会两倍于选择另一个网页的人数。虽然个体选择非常难预测，作为一个整体时却遵循着严格的模式。

偏好连接在好莱坞同样发挥作用。制片人的工作是让电影赢利，他们深知影星可以让电影卖座。因此，选择演员时需要考虑两个相互矛盾的因素：演员与角色的匹配度以及演员的知名度。这两个因素给选择过程带来了同样的偏见。链接数多的演员有更多的机会得到新角色。事实上，一个演员出演的电影越多，就越有可能再次出现在导演的选择范围内。在这里，立志出演好角色的演员会面临巨大的劣势。好莱坞内外的人都知道一个看似矛盾的观点：为了得到好的角色，你需要先出名，而想出名又需要先得到好的角色。

链接洞察

万维网和好莱坞网络让我们不得不放弃随机网络固有的第二个重要的假设——平等特性。在埃尔德什-莱利和瓦茨-斯托加茨的模型中，网络的节点没有差异，因此，所有节点以同样的可能性获得链接。前文探讨的例子却是另外一幅情形。拥有较多链接的网页更有可能被连接，连接度高的演员更有可能得到新角色，引用次数多的论文更有可能获得新的引用，连接者会结交更多的朋友。网络演化由偏好连接这个微妙而不可抗拒的定律支配着。受该定律的影响，我们会在无意间以更高的速度向已经拥有大量链接的节点添加新链接。

生长机制和偏好连接，支配真实网络的两大定律

将上述难题的各个片段放到一起，我们发现，真实网络由两个定律支配着：生长机制和偏好连接。每个网络都是从一个小的核开始，通过添加新的节点而增长。然后，这些新节点在决定连向哪里时，会倾向于选择那些拥有更多链接的节点。这些定律和以前的模型明显不同——以前的模型假设网络中的节点数目是固定的，节点之间是随机连接的。但是，生长机制和偏好连接这两个定律，是否已经足以解释真实网络中碰到的枢纽节点和幂律呢？

为了回答该问题，在1999年发表在《科学》杂志上的论文中，我们提出了一个包含这两个定律的网络模型。模型很简单，根据生长机制和偏好连接，网络生成算法可以通过下面两个直接的规则定义出来。

A.生长机制：每个阶段，我们向网络中添加一个新节点。该步骤强调网络每次增加一个节点。

B.偏好连接：我们假定每个新节点和已经存在的节点之间形成两个链接。选择给定节点的概率正比于该节点拥有的链接数。也就是说，如果有两个节点可供选择，其中一个节点的链接数是另一个的两倍，链接数多的节点被选到的概率也是另一个节点的两倍。

每重复步骤（A）和（B）一次，就有一个节点添加到网络中。因此，通过逐个添加节点，我们生成了一个持续增长的网络（见图7-1）。该模型将生长机制和偏好连接结合在一起，是我们解释枢纽节点的第一次成功尝试。雷卡的计算机模拟结果很快表明，该模型能够产生幂律。这个模型首次解释了真实网络中观测到的无尺度幂律，它很快就以无尺度模型的名字闻名遐迩。

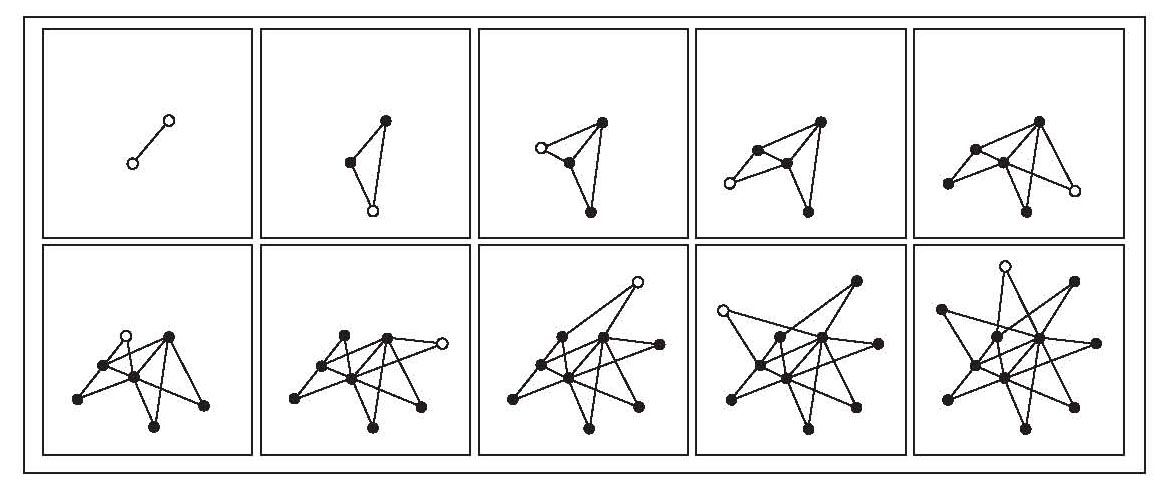
无尺度拓扑是真实网络持续生长特性的自然结果。开始时，网络中仅有两个相互连接的节点（左上图），在后续的每个子图中，一个新的节点（用空心圆表示）被添加到网络中。在决定连向哪里时，新节点倾向于连接那些连接度高的节点。由于生长机制和偏好连接，一些高度连接的枢纽节点出现了。

图7-1 无尺度网络的诞生

无尺度网络的诞生

为什么无尺度模型能够产生枢纽节点和幂律呢？首先，生长机制发挥着重要作用。网络生长意味着早期的节点比后来的节点有更多的时间获取链接：如果某个节点是最后一个到达的，就没有其他节点有机会去连接它；如果某个节点是网络中的第一个节点，所有随后到达的节点都有机会连接它。因此，生长机制让资历老的节点具有明显的优势，让它们拥有最多的链接。然而，资历还不足以解释幂律。枢纽节点还需要第二个定律的帮助，那就是偏好连接。由于新节点倾向于连接那些连接度高的节点，而早期的节点拥有更多的链接，更有可能被选到，因此会比后来的节点和连接度低的节点生长得更快。随着越来越多的节点加入，并且选择连接那些连接度较高的节点，最早的那些节点必将脱颖而出，获得非常多的链接，变成枢纽节点。因此，偏好连接引入了富者愈富的现象，帮助连接度较高的节点得到更多的链接，而后来者的链接数会相应地减少。

富者愈富现象自然导致了真实网络中观察到的幂律。事实上，我们进行的计算机模拟表明，对于任意的k，具有k个链接的节点数目遵循幂律分布。刻画幂律分布的参数，即度指数，其精确值也不再神秘。使用数学工具——这里是指我们提出的连续介质理论（continuum theory），便能用解析方法计算出度指数的值。实际上，根据偏好连接，每个节点吸引新链接的速率正比于它目前拥有的链接数。借助这个简单的观察，我们能够提出一个简单的方程来预测节点随着网络增长所能够获得的链接数。这个办法使我们能够用解析方法计算出度分布，并证实度分布的确遵循幂律^[1]。

生长机制和偏好连接能够单独解释幂律吗？计算机模拟和计算的结果告诉我们，二者对于无尺度网络的生成都是必要的。没有偏好连接的生长网络具有指数度分布，它和钟形曲线类似，不允许枢纽节点出现。没有生长机制，我们就回到了静态的模型，因而不能产生幂律。

不断完善的无尺度网络理论

我们提出无尺度模型的目标非常小：证明生长机制和偏好连接这两个简单的定律就能够解决枢纽节点和幂律出现的难题。因此，该模型对后续研究的巨大影响让我们感到很欣慰，也很吃惊。这可能因为，为了让模型简单而透明，我们从一开始就忽略了影响真实网络拓扑结构的很多因素。最明显的一个因素是，无尺度模型中的所有链接都是在新节点加入网络时出现的，而大多数网络中，新链接是可以自发出现的。例如，当我在主页上添加一个指向nytime.com的链接时，我实际上是在两个老节点间创建了一个内部链接。在好莱坞，94%的链接是内部链接，它们是在两个成名演员第一次合作时形成的。无尺度模型中缺少的另一个特性是很多网络中的节点和链接可以消失。实际上，有很多网页消失了，并带走了数千链接。链接还可以重连，譬如，我可以把指向CNN.com的链接换成指向nytimes.com的链接。上述以及其他更多的在一些网络中经常出现而在无尺度模型中缺少的现象表明，真实网络的演化比无尺度模型所预言的要复杂得多。为了理解复杂世界里的网络，我们必须把这些机制整合到一个一致的网络理论中，并解释它们对网络结构的影响。

将关于无尺度模型的论文投稿之后，雷卡·阿尔伯特和我开始研究内部链接和重连这样的过程对无尺度网络结构的影响。但是，做这些研究的人不再只有我们。在投到《科学》杂志的论文发表一个月后，我了解到，世界各地有不少实验室在进行类似的研究。我长期的合作者路易斯·阿马拉尔（Luis Amaral）当时是波士顿大学的教授，他正在扩展无尺度模型。他引入了年龄因素，让节点可以“退休”，即停止获取链接。和阿马拉尔一起研究的人还有斯坦利以及他的两个学生安东尼奥·斯卡拉（Antonio Scala）和马克·巴泰勒米（Mark Barthélémy）。他们指出，如果节点在某个年龄后能够停止获取链接，枢纽节点的大小将是有限的，大的枢纽节点将比幂律预测的要少。同时，何塞·门德斯和谢尔盖·多罗戈夫切夫（Sergey Dorogovtsev）正在波尔图独立地研究类似的问题。他们很快就发表了一系列关于无尺度网络的极具影响力的论文中的第一篇。假设节点随着年龄增加逐渐丧失吸引链接的能力，门德斯和多罗戈夫切夫指出，逐渐老化没有破坏幂律，只是改变了度指数，从而改变了枢纽节点的个数。来自波士顿大学的保罗·克拉皮夫斯基（Paul Krapivsky）和希德·雷德纳，与来自墨西哥的弗兰索瓦·列夫拉兹（Francois Leyvraz）一起泛化偏好连接。他们认为，与给定节点连接的概率不仅是简单地和该节点拥有的链接数成正比，而是可以遵循更复杂的函数。他们发现，这样的扩展会破坏掉刻画网络的幂律。

链接洞察

这些是物理学家、数学家、计算机科学家、社会学家和生物学家在仔细研究无尺度模型及其各种扩展时得到的大量后续结果的一部分。由于他们的努力，我们现在有了一个丰富而一致的关于网络生长和演化的理论，这在几年前是无法想象的。我们知道了，内部链接、重连、节点和链接的删除与老化、非线性因素以及很多其他影响网络拓扑的过程，都可以无缝地整合到一个令人吃惊的网络演化理论架构中，无尺度模型是它的一个特例。这些过程改变了网络生长和演化的方式，也必然会改变枢纽节点的个数和大小。不过，在大多数情况下，生长机制和偏好连接都是同时出现的，枢纽节点和幂律也是同时出现的。在复杂网络中，无尺度结构不再是例外，而是正常现象，这也是它之所以出现在大多数真实系统中的原因。

无尺度模型，一种全新的建模思想

过去三年里提出的演化网络理论，是网络建模的单向前进标志。通过将网络视为随时间持续变化的动态系统，无尺度模型体现了一种新的建模思想。始于埃尔德什和莱利的经典静态模型，只是尝试如何组织固定数目的节点和链接，使最后得到的网络和要建模的网络吻合。这个过程和画图是类似的。坐在一辆法拉利面前，我们的任务是为它画像，让所有人都能认出这辆轿车。然而，完全写实的画法并不能帮助我们理解轿车的制造过程。而我们想知道如何构建一辆和原来那辆轿车一样的轿车。这正是各种网络演化模型想要完成的目标。它们通过再现大自然创造各种复杂系统的步骤，来掌握网络是如何组装的。如果能够正确地建模网络组装过程，最终得到的网络就能够和现实紧密匹配。因此，我们的目标已经转变了，从描述网络拓扑转到了理解塑造网络演化的机制上。

研究焦点的转变带来了网络语言的巨大变化。在我们不得不引入生长机制之前，经典模型的静态特性一直没有人注意。类似地，在幂律要求我们引入偏好连接之前，随机性也不是什么问题。结构和网络演化不能彼此分开，认识到这一点之后，我们很难再回到主宰我们思维方式几十年之久的静态模型。这种思维方式的转变缔造了一组反义词：静态和生长，随机和无尺度，结构和演化。

在上一章的末尾，我们提出了一个重要的问题：幂律的出现是否意味着真实网络是从无序到有序的相变的结果？我们得出的答案非常简单：网络不是处于从随机状态到有序状态的途中。网络也不是处于随机和混沌的边缘。相反，无尺度拓扑预示着，某种组织原则在网络形成过程的每个阶段都发挥着作用。这一点都不神奇，因为生长机制和偏好连接可以解释自然界所见网络的基本特征。无论网络变得多么大、多么复杂，只要偏好连接和生长机制出现，网络都将保持由枢纽节点主导的无尺度拓扑。

如果没有后续的发现，无尺度模型可能只是一个有趣的学术问题。其中最重要的发现是，人们认识到大多数具有重要科学和现实意义的复杂网络都是无尺度的。万维网的数据大而详细，足以让我们相信幂律可以描述真实网路。这一认识触发了一系列的发现，一直延续至今。好莱坞网络，细胞内的代谢网络，引文网络，经济网络和语言网络都属于无尺度网络，一时间，无尺度拓扑形成的原因在很多科学领域变得重要起来。^[2]无尺度模型中支配网络演化的两个定律为探索各种各样的系统提供了一个很好的出发点。

首先，幂律让枢纽节点变得合理了。随后，无尺度模型将真实网络中看到的幂律提升到拥有数学支撑的理论高度。网络演化的复杂理论使我们能够精确地预测尺度指数和网络演化，使我们对复杂互联世界的理解上升到一个新水平，让我们比以前任何时候都更接近对复杂性架构的理解。

然而，无尺度模型提出了一些新问题。其中一个问题不断浮现：在富者愈富的世界里，后来者如何取得成功呢？对这个问题的探索把我们带到了一个似乎不太相关的领域：20世纪初量子力学的诞生。

[1] 无尺度模型的度指数γ=3，也就是说，度服从P（k）～k^-3。

[2] 已经有多个研究组证明，语言具有无尺度特性。在语言网络中，节点是词，链接表示词在文本中的共现关系或者语义关系（同义词或反义词）。