第五章　准　确　度

让我们首先比较模拟计算机和数字计算机的运用。

除了其他各方面的考虑外，模拟计算机的主要局限性是它的准确度问题。电模拟机的准确度难得有超过1∶10³的，甚至机械的模拟机（如微分分析机）在最好的情况下也只能达到1∶10⁴至1∶10⁵。而另一方面，数字计算机却能达到任何我们所需要的准确度。比如，我们已经讲过，12位十进制计算机，就标志着1∶10¹²的准确度（我们在后面还要进一步讨论，这已经标志着现代计算机的相当典型的准确度水平）。还应该注意，数字计算机要提高准确度的话，比模拟机容易。对微分分析机来说，从1∶10³提高到1∶10⁴的准确度，还比较简单，从1∶10⁴要提高到1∶10⁵，就已经是现有技术所可能达到的最佳结果；用目前已有的方法，再要使准确度从1∶10⁵提高到1∶10⁶，则是不可能的了。而另一方面，在数字计算机中，使准确度从1∶10¹²提高到1∶10¹³，仅仅是在12位数字上加上1位，这通常只意味着在设备上相对地增加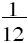＝8.3％（而且还不是计算机装置的每一部分都要如此增加），同时在速度上只损失同一比例（也不是每一处的速度都要损失），这两者的变化，都是不严重的。拿脉冲密度系统和模拟系统来比较，脉冲密度系统的准确度更差。因为在脉冲密度系统中，1∶10²的准确度要求在时间间隔t₁中，有10²个脉冲，就是说，单单就这个因素来说，机器的速度就要减少100倍。速度按这样的数量级减少，是不妙的，如果要作更大的减少，一般就认为是不能允许的了。

需要高度的准确度（数字的）之理由

可是，现在会产生另外一个问题，为什么这样高度的准确度（例如在数字计算机中为1∶10¹²），是必要的呢？为什么典型的模拟机（1∶10⁴）或甚至脉冲密度系统（1∶10²）的准确度是不够的呢？我们知道，在大多数应用数学问题和工程技术问题中，许多数据的准确度不会优于1∶10³或1∶10⁴，甚至有时还达不到1∶10²的水平。所以，它们的答案也用不着达到更高的准确度，因为这样提高准确度是没有意义的。在化学、生物学或经济学的问题中，或在其他实际事务中，准确度的水平甚至还要低一些。可是，在现代高速计算方法的一贯经验中，都说明了：对于大部分的重要问题，甚至1∶10⁵的水平还是不够用的。具有像1∶10¹⁰和1∶10¹²准确度水平的数字计算机，在实践中已被证明很有必要。这个奇怪的现象之理由，是很有趣和很有意义的。它和我们现有的数学的与数值过程的固有结构有关。

标志这些过程的特性的事实是：当这过程分析为它的各个组成元素时，过程就变得非常长了。对所有适于运用快速电子计算机的问题来说（即至少是具有中等复杂程度的问题），都是如此。根本的理由，是因为我们现在的计算过程，要求把所有的数学函数分析为基本运算的组合，即分析为算术四则运算或其他大致相当的运算程序。实际上，绝大多数的函数只能用这种方法求得近似值，而这种方法意味着在绝大多数情况下，需要很长的、可能是迭代的一序列基本运算（见前文所述）。换句话说，必要的运算之“算术深度”，一般是很大的。还应指出，它的“逻辑深度”则是更大的；同时，由于一个相当重要的原因——比如：算术四则必须分解为基本的逻辑步骤，因而每一次运算本身都是一条很长的逻辑链子。但是，我们这里只需要谈谈算术深度的问题。

如果有很大量的算术运算，则每一次运算所出现的误差是叠加的。由于这种误差主要地（虽然还不是完全地）是随机的，如果有N次运算，误差将不是增加N倍，而是大约增加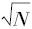倍。仅从这一点道理来说，要得到一个1∶10³准确度的综合结果，还不需要每一步运算都要达到1∶10¹²的准确度。因为只有当N为10¹⁸时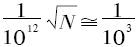，。而在最快速的现代计算机中，N也很难得大于10¹⁰。（一个计算机，每一步算术运算只需要20微秒，充其量来说，每个问题大约要解48小时，即使这样，N也只是10¹⁰左右！）。但是，我们还得考虑其他的情况。在计算过程中所进行的运算，会把前一步运算所发生的误差放大了。这将会极快地超过于刚才讲过的每一步准确度与要求综合结果的准确度之间的数字差距。上面讲过，1∶10³被1∶10¹²除，得10⁹；但是，只要有425次顺次的运算，如果每一步运算只发生5％的误差，依次递增的结果，就会达到10⁹的误差了。我在这里，不准备对此问题作具体的、实际的估计，特别是因为计算技术中已有不少办法减低这个效应。但不管怎样，从大量经验所得到的结论来看，只要我们遇到的是相当复杂的问题，上述的高度准确度水平是完全必要的。

在我们离开计算机的直接问题之前，我还要讲一下关于计算机的速度、大小以及诸如此类的事情。