附录：

冯·诺伊曼评传

胡作玄

（中国科学院数学与系统科学研究院研究员）

冯·诺伊曼是20世纪最出名的数学家之一。可能这主要是由于他在电子计算机方面的开创性工作。为此，许多人甚至给他戴上“计算机之父”的桂冠。虽然计算机的研究足以使他永垂不朽，但是单凭这方面来衡量他一生的工作就未免失之过偏，这只不过是他工作的一小部分。

约翰·冯·诺伊曼是20世纪最出名的数学家之一，这可能主要是由于他在电子计算机方面的开创性工作。为此，许多人甚至给他戴上“计算机之父”的桂冠。虽然计算机的研究已足以使他永垂不朽，但是单凭这方面来衡量他一生的工作就未免失之过偏，这只不过是他工作的一小部分。他在纯粹数学、应用数学、计算数学等许多分支都有重大的也往往是开创性的贡献。

冯·诺伊曼的一生也可以借用本系列丛书中《控制论》、《人有人的用处》的作者维纳（Norbert Wiener，1894—1964）的三本传记的书名来概括：两本是维纳的自传：《昔日神童》、《我是一位数学家》，一本是别人写的维纳传记《信息时代的隐匿英雄》。冯·诺伊曼的一生是天才的一生，而且前半生的贡献主要是数学，他对数学的贡献有着不可忽视的影响。第二次世界大战爆发后，他参与了原子弹的研制以及电子计算机的研发。后者直接影响了当代社会的发展，冯·诺伊曼无疑是信息时代的英雄。

生　　平

一、家世——匈牙利的犹太人

冯·诺伊曼1903年12月28日出生于匈牙利布达佩斯。当时匈牙利是奥匈帝国的一个组成部分。他的家族是犹太裔，父亲马克斯（Max von Neumann，1870—1929）是银行家，1913年被奥地利皇帝封为贵族，于是其姓氏中出现了冯（von）字。这样，匈牙利、犹太人、银行家、贵族就成为冯·诺伊曼身世的主题词。

1950年：参观者和部分制造ENIAC的人员合影。左边第二个是冯·诺伊曼。

中国人对匈牙利也许并不陌生，它使我们联想到匈奴。匈牙利人是否为匈奴后裔，史学家仍然有争议，可是有一点很明显，匈牙利虽然地处欧洲大陆的中心，但与欧洲三大主流族群——拉丁族、条顿族（即日耳曼族）、斯拉夫族都毫无亲缘关系，语言也不属于印欧语系。匈牙利人的姓名写法也同中国人一样，是姓在前、名在后，其他大部分欧洲人姓名写法则颠倒过来。

我们很熟悉匈奴的历史。公元1世纪到5世纪，匈奴的一支由中国的北方一直打到欧洲。东汉窦宪伐匈奴，匈奴西徙。他们一溜烟跑了上万里。虽然是汉朝的手下败将，到欧洲可神气了一番。偌大的罗马帝国，连同周围的蛮族，被匈奴打得七零八落。当时匈奴的首领叫阿提拉（Attila，约406—453），被欧洲人称为“上帝之鞭”。阿提拉去世后不久，西罗马帝国灭亡，匈奴人也不知上哪儿去了。

公元500年到1000年，这段历史就不那么清楚了。只是这500年的末期，里海北岸的马扎尔（Magyar）人，移居到欧洲中部，在现在的匈牙利附近定居下来。

公元1000年左右，马扎尔人信仰基督教，这和当时许多中欧、东欧、北欧的民族，如德国人、俄国人、瑞典人、波兰人一样，除了后来被土耳其统治的地方之外，欧洲已全部基督教化。

从那时起，匈牙利的大平原以及北部、西部的丘陵就成为四邻滋扰之地。13世纪，蒙古人来过，幸而没有西进。接着就是土耳其，土耳其人占了匈牙利许多土地，直到18世纪初才全部撤出。16世纪初，奥地利的哈布斯堡王朝也占领了匈牙利的一部分，在18世纪初，把整个匈牙利据为己有。那时候，奥地利可是欧洲的四强（英、法、俄、奥）之一。19世纪中逐渐衰败，其强国地位最后被统一的德国所取代。

普鲁士后来迅速崛起。普奥战争，普法战争以及普鲁士最终统一德国，并把日耳曼诸国的老大——奥地利排除在外，这一切改变了欧洲的命运、改变了奥地利的命运，也改变了匈牙利的命运。所有这些都发生在奥地利皇帝弗兰茨·约瑟夫（Franz Joseph，1830—1916，1848—1916在位）的身上。他18岁当了皇帝，在位近70年。尽管如此，一般人并不知道他是何许人也，可是很多人听说过他的皇后——美丽、善良而又薄命的希西（Sissy即Elizabeth，1837—1898）公主。希西公主在提高匈牙利的地位上也起着重要作用。

1867年奥地利和匈牙利成为理论上平起平坐的二元的奥匈帝国，不过奥地利皇帝兼任匈牙利国王。奥地利仍是老大，匈牙利可算是老二，这时的匈牙利比现在大多了，包括现在的斯洛伐克到克罗地亚。这50年匈牙利迎来了它的繁荣时期，匈牙利的犹太人也有机会脱颖而出。

说起犹太人，需要长篇的历史叙述他们的不幸遭遇。19世纪中期，欧洲犹太人由西向东逐步获得“解放”，也就是不再限制他们住在一定的犹太定居区中，以及可以受一定的教育。不过在东欧，特别是俄国，排犹事件屡有发生。19世纪末到20世纪初，对付犹太人使当局大伤脑筋。1906年俄国的财政大臣说，犹太人太机灵，以至于常常超越限制他们的任何法律。于是当局采取“三三制”的方法：让1/3犹太人皈依东正教，把1/3犹太人驱逐出境，把另外1/3犹太人杀死。其他国家做法大同小异，只是没有俄国那么残酷。被驱赶的犹太人到哪里去呢？1890年，哪里是犹太人的天堂呢？一个是美国纽约，一个就是匈牙利的布达佩斯。

布达佩斯成为“欧洲的耶路撒冷”看来是挺奇怪的事。实际上，在不同文化中生存是绝对不容易的事。匈牙利的犹太人尤其如此。在中欧，只有匈牙利人抵抗住周围欧洲的文明，特别是日耳曼化，顽强地使匈牙利文化坚持下来，而处在匈牙利人包围之中的犹太人要在这种双重压力下生存则更加艰难。随着匈牙利地位的提升，匈牙利大地主大贵族仍然占有大量的土地，而工业发展为犹太人提供了经商致富的机会，他们成为城市的资产阶级，经营银行、工商业、外贸、各种制造业。富起来的犹太人子弟很快受到很好的教育，成为精英阶层。这样一来，连保守的奥地利皇帝也不得不对他们另眼相看。在一个封建贵族占统治地位的国家，他们靠贵族头衔与有钱人达成妥协，整个19世纪不到100家犹太人受封为贵族，而20世纪的前13年间已有220家受封，冯·诺伊曼的父亲就是其中之一。

匈牙利人，特别是其中占5％的犹太人并没有浪费1867年到1918年这50年的大好时机。这样一个小国家50年间产生出不成比例的文化名人，而其中绝大多数都是犹太人。

这简直是一个奇迹，1900年前后涌现了一大批有国际声望的大科学家：“超音速航空之父”冯·卡门（T.von Karman，1880—1963），原子弹的首倡者齐拉（L.Szilard，1898—1964）、“氢弹之父”特勒（Edward Teller，1908—2003）。当然，20世纪最显赫的科学界荣誉莫过于诺贝尔奖了，百年之中，匈牙利裔的科学家获奖6人（作为对比，华裔科学家及日裔科学家各有6人获奖），他们是“全息术之父”伽博（Dennis Gabor，1900—1981，1971年获物理学奖），冯·诺伊曼的好友维格纳（Eugene Wigner，1902—1995，1963年获物理学奖），因研究维生素C而出名的圣·乔奇（Szent-Györgyi von Nagyrapolt，1893—1986，1937年获生理学或医学奖），发现示踪原子方法的海维希（Georg von Hevesy，1885—1966，1943年获化学奖），弄清耳朵（具体讲是耳蜗）为什么能听到声音的贝凯西（Georg von Békésy，1899—1972，1961年获生理学或医学奖），以及耳科学的创立者之一巴拉尼（Robert Bárány，1876—1936，1914年获生理学或医学奖）。

当然匈牙利也产生了许多其他文化名人。最著名的有诗人裴多菲（Sandor Petöfi，1823—1849），他的诗“生命诚可贵，爱情价更高……”在中国脍炙人口，不过他是老一代的人物了。新一代的人物有作家克斯特勒（Arthur Koestler，1905—1983），他还特别研究天才创造性劳动；西方马克思主义的奠基人卢卡奇（George Lukács，1885—1971）；经济学家卡尔多（Nicholas Kaldor，1908—1986）。有意思的是，匈牙利人的发明往往和一般老百姓密切相关，一个是鲁比克（Erno Rubik，1944—　）发明的魔方，在20世纪80年代风行全世界，圆珠笔也是匈牙利人拜罗（Laszlo Biro，1900—1985）发明的，在英国拜罗不仅是商标的名字，而且还成了圆珠笔的代名词。

国际政治、经济界也逐渐有匈牙利裔人涌现。在当前经济危机中，最著名的“金融大鳄”索罗斯（Soros George，1930—　），是匈牙利犹太人，我们不应该忘记他也是捐款最多的慈善家之一。当然，现在的法国总统萨科奇（Sarkozy Nicolas，1955—　）也是匈牙利人。至于数学家就更多了，比如古典分析大师费耶（Lipot Fejer，1880—1959），波利亚（George Pólya，1887—1985）、赛格（Gabor Szëgo，1895—1985），泛函分析的缔造者之一里斯（Frigges Riesz，1880—1956），他的弟弟迈克尔·里斯（Marcel Riesz，1886—1969）也是数学分析专家，哈尔（Alfréd Haar，1885—1933）则因哈尔测度而知名，拉多（Tibor Radò，1895—1965）则率先解决极小曲面的问题。此外数论专家爱尔特希（Paul Erdös，1913—1996），瑞尼（Alfréd Renyi，1921—1970）也都是国际知名的第一流的数学家。后来匈牙利仍然一代一代产生出大数学家，如阿贝尔奖获得者拉克斯（Peter Lax，1926—　）以及现在国际数学联盟主席洛瓦斯（László Lovász，1948—　）。不管怎么说，冯·诺伊曼是他们中间的佼佼者。

二、天才的成长（1903—1921）

冯·诺伊曼出生时，父亲马克斯已是一位富有的犹太银行家。1913年，还荣获贵族封号，这成了他们姓中von（冯）的来源。约翰是马克斯三个儿子中的长子，他的弟弟迈克尔（Michael von Neumann）和尼古拉斯（Nicholas von Neumann）分别于1907年和1911年出生。他一出世就受到各方面的关心和照顾。他从小就接受家庭教师的教育，很快就掌握了德语和法语。他的父亲十分关心儿子的成长，很早就注意到他智力不同寻常：他有惊人的记忆力、理解力、心算能力、语言能力以及创造才能，的的确确是一个全面的天才。他不只小时是神童，而且许多“超人的”能力一直保持到成年。

他的记忆力简直像照相机，只要看一眼电话号码本，他就能把人名、住址、电话号码记得牢牢的。以至于后来在纽约曼哈顿区，他也根本不用厚厚的电话号码本。当然这也许是机械记忆，不足为奇。可是，他还能把整段、整章的小说背诵得一字不差。

他6岁就会心算8位数除8位数，后来对于公式的运算也能很快在头脑中进行。可是，早在一百多年前，数学家早就不把计算尤其是心算才能当成什么了不起的事了。大数学家庞加莱就常常以自己做加法总要出错而“自豪”。数学才能更多地表现在抽象概念理解力、逻辑推理思维能力，以及解决问题的能力等方面。而在这些方面，冯·诺伊曼也早就显示非凡的能力。8岁时，他在别的小孩刚上小学学加减乘除的时候就已经掌握了微积分，到12岁，他已能读懂法国大数学家波雷尔（E.Borel，1871—1956）的专门著作《函数论》了。

1914年，也就是第一次世界大战爆发那年，他进路德教会中学学习。这所学校是布达佩斯最好的三所中学之一，学生中近一半是犹太人。没几天，富有责任心的数学老师拉兹（Ladislas Ratz）就告诉马克斯，小约翰的数学才能过人，建议请大学教师个别辅导以全面发展他的天才。经拉兹的介绍，年轻数学家费凯特（M.Fekete，1886—1957）定期到冯·诺伊曼家里进行辅导。在中学快毕业时，费凯特和冯·诺伊曼合作，对布达佩斯大学教授费耶的一个分析定理加以推广，这成为冯·诺伊曼的第一篇论文，当时他还不到17岁。后来费凯特本人一直局限在古典分析这个狭窄领域里进行研究，而冯·诺伊曼很快深入到最新的数学——20世纪的数学——集合论、测度论、泛函分析等新分支中去。还在中学时，他已经开始自学这些课程。

除了数学课之外，冯·诺伊曼还跟同学一起学习其余课程，一起参加各种活动。他功课很好，但也不是门门得A，制图课他就只得个B。他体育也不太好，他不太喜欢户外运动，只是冬天偶尔出去滑雪。他喜欢聊天，维格纳比他高一班，他们经常在一起谈数学，一谈起来就没完没了。他喜欢下棋，但也不是老赢。他和大家相处得很好，不骄傲，但和谁也没有过分亲密的关系。这一方面由于他感情从不外露，另一方面也由于他有许多额外精神需要，除了数学，他如饥似渴地读历史。他从小就喜欢历史，小时候就啃德国历史学家翁肯（Wilhelm Oncken，1835—1905）编写的45卷《通史》；他对千年拜占庭的历史的熟悉程度只有专家可比；他对美国历史也非常熟悉，有一次去杜克大学开会，他们经过美国南北战争的战场，他对于这场战争的细枝末节都说得一清二楚，使美国人都惊叹不已。他对历史的超人洞察力，对他后来的战略思想至关重要。他还通过阅读文学作品学习语言，年纪很大时，他还能背诵《双城记》中前十几页。而在这些方面，没有游伴能完全满足他，这也许就是所谓“天才的孤独”吧！

1918年底，奥地利哈布斯堡王朝覆灭，第一次世界大战以同盟国的失败而告终。1919年3月，贝拉·库恩（Bela Kun）建立起苏维埃革命政府，首先采取的政策就是没收银行。革命还不到一个星期，冯·诺伊曼全家就逃离匈牙利。1919年8月，霍尔蒂在外国军队的干预下，推翻革命政府，建立独裁政权。他们歧视犹太人，歧视知识分子，镇压左翼同情者。冯·诺伊曼一家从国外回来，他继续上学，父亲继续开银行，可是大战以前的好时光一去不复返了。1921年，冯·诺伊曼参加中学毕业会考，同时获得了厄特沃什（Eötvös）奖。后来，他又在匈牙利的数学竞赛中轻而易举地得到第一名。

有天才的人未必有成就，有成就的人未必有天才。幸运的是，冯·诺伊曼兼具天才和成就于一身。他没有像罗素那样在家自由放任，也没有像维纳那样越级跳班受到许多额外功课的压力。冯·诺伊曼按部就班上中学，在课余吸收了大量的知识。他有如此超强的自学能力，以至于任何书本知识、任何考试对他来说都是小菜一碟。

三、大学时代（1921—1926）

中学毕业后自然要上大学。父亲知道冯·诺伊曼有志于学数学，但是出于未来就业上的原因劝他放弃，匈牙利只需要几位数学家就够了。有钱的犹太人都会培养自己的子弟上大学，但匈牙利的大学资源相对有限，要获得最好的教育，非得去国外的一流大学不可。作为父子妥协的结果，冯·诺伊曼答应到国外攻读化学。布达佩斯大学欢迎他去，入学要的“清白纪录”也不成问题。但是，他深知匈牙利并非久留之地，只有德国、瑞士等地才是真正的科学乐园。因此，从1921年中学毕业之后，德国成为他成长的主要地方。

1921年到1925年，冯·诺伊曼在布达佩斯大学注册数学博士研究生，但他从来没有在那听课，只是学期末参加考试。从1921年到1923年，他主要在柏林大学学习化学，而从1923年到1925年主要在瑞士著名的联邦工业学院上课。虽然1925年他在联邦工业学院拿到化学工程文凭，但是他主要听的还是数理方面的课程（如1922年他在柏林听过爱因斯坦统计物理学的课），并同各地数学家交往。当时，他主要受施密特（E.Schmidt，1876—1959）和外尔（H.Wey1，1885—1955）的影响。他们都是希尔伯特的学生，他们的早期工作都受到希尔伯特思想的巨大影响。施密特把希尔伯特的积分方程理论抽象化，后来，这成为希尔伯特空间概念的来源。外尔则是希尔伯特的谱理论的继承人，同希尔伯特一样，外尔对当时新兴的理论物理学极有兴趣，而且致力于把数学应用于解决相对论、量子论及古典物理的问题。冯·诺伊曼的早期工作反映了希尔伯特和外尔的共同之处，他们都相信数学在发现物理学的普遍规律方面作用极大，反过来，物理学也是启发最好的数学思想的源泉。

冯·诺伊曼还直接受到希尔伯特的巨大影响。在大学时期，他有时到格丁根去拜访希尔伯特，这两位相差四十多岁的数学家，常常一起在希尔伯特的花园或书房一起交谈好几个小时。希尔伯特对数学及物理学的公理化思想，以及他当时对数学基础以及对物理学的兴趣都大大影响了冯·诺伊曼并决定了他早期工作的方向。

在1921年到1926年五年中，他并没有放弃数学，相反，他在布达佩斯大学申请做博士生，这个时期主要研究方向是数理逻辑。1926年春天，冯·诺伊曼取得布达佩斯大学博士学位，论文题目是《集合论的公理化》。实际上，他在上大学时期就已经对数学基础进行系统的研究，并发表了几篇论文。

冯·诺伊曼吸收希尔伯特的公理化思想，致力于把集合论的基本概念弄清楚并加以公理化。小小年纪，他就已经深入思考当时这类头等重要的问题了。1923年，冯·诺伊曼发表他在数学基础方面的第一篇文章，这时他还不到20岁。

冯·诺伊曼喜欢公理化的道路，这预示了他今后从事数学研究的主要方法。在这方面，早在1908年策梅洛（E.Zermelo，1871—1953）已经提出了一个公理系统，这个系统基本上不错，经过弗兰克尔（A.Fraenkel，1891—1965）等人改进以后成为著名的ZF系统，这是集合论中最常用的公理系统。年轻的冯·诺伊曼很欣赏公理化这条路，但是他对策梅洛的公理系统进行了一些根本上的修改。他把论文送到《数学杂志》发表，当时该杂志的编辑施密特要弗兰克尔审稿。冯·诺伊曼还是名不见经传的年轻人，可是弗兰克尔从文章中就看出作者身手不凡。审稿者当时不能完全理解这篇文章，于是邀请冯·诺伊曼到马堡大学来。他们讨论了许多问题。因为原来那篇文章不好懂，弗兰克尔建议他写一篇短文来阐述自己的方法和结果，这就是《集合论的一种公理化》，1925年发表在弗兰克尔担任编辑的《纯粹与应用数学杂志》上。而原来的论文《集合论的公理化》一直到1928年才问世。这些论文也是他1926年在布达佩斯大学的博士论文的基础。

当时，关于数学基础的论战非常热闹，冯·诺伊曼坚决支持希尔伯特的形式主义路线，反对逻辑主义和直觉主义。1930年，在德国哥尼斯堡的会议上，冯·诺伊曼对形式主义做了系统总结报告。希尔伯特提出了证明算术及分析的无矛盾性的计划，冯·诺伊曼完成了在特殊情形下的算术无矛盾性的证明，但分析的无矛盾性的证明总也没有成功。冯·诺伊曼那时每天工作到深夜，上床睡觉之后还常常半夜醒来。有一次他梦见他有办法克服全部困难，于是起身写下来。不过最后他还是发现一个漏洞补不起来。他后来开玩笑说：“数学是多么走运呵，因为我第三个晚上没有做梦。”冯·诺伊曼关于数理逻辑的工作对以后计算机及自动机理论有着不可忽视的影响。

四、德国的数学中心（1926—1930）

冯·诺伊曼关于数学基础方面的工作受到希尔伯特的注意。1926年初，希尔伯特向洛克菲勒基金会提出申请，资助冯·诺伊曼到格丁根来。负责人照例看资格行事，这位还没有拿到博士学位的22岁的年轻人当然不在考虑之列。后来由于库朗（R.Courant，1888—1972）教授的帮助，1926年秋天，冯·诺伊曼到格丁根当希尔伯特的助手。这使他在学术方向上有了一个大变化。当时正是量子力学光辉的开创时期，在格丁根这个量子力学的中心之一，谁又不被这门新兴物理学所吸引呢？希尔伯特也不例外，他对物理学早就有兴趣，他的目标就是把物理学公理化，不管是经典物理学还是相对论与量子论。他原想请冯·诺伊曼同他一起搞自己的元数学纲领（即希尔伯特计划），可是冯·诺伊曼又何尝像希尔伯特的另一些助手和学生一样而只能搞某一方面的问题呢？到了格丁根，他来了一个小小的改行，这次改行正如他以后的每次改行，都给数学带来丰硕的成果。1925年海森伯的矩阵力学和1926年薛定谔的波动力学的创立标志量子力学的诞生。物理学家热烈地争论基本的物理概念，而除了少数人（如泡利、玻恩等）之外，他们的数学修养还不足以给量子力学很好的数学表述。玻恩说，1924年大多数物理学家连矩阵也没听说过。而薛定谔方程，就连薛定谔本人一开始也不会解。虽然早已有了数学工具，但是需要有数学家弄好了装到盘子里端上来，否则物理学家就会发明出让数学家感到莫名其妙的东西，如狄拉克的函数。冯·诺伊曼在这时来到格丁根使物理学和数学都大为走运，他给量子力学奠定了数学基础，同时发展了希尔伯特空间的算子理论。这是物理学和数学相得益彰的范例。要是没有冯·诺伊曼，这个过程可能会更曲折，决不会一下子在两方面都成为“经典的”、标准的、指导后来发展的工作。

1926年秋天，希尔伯特主持物理学的讨论班，请海森伯在讨论班上做第一个报告。冯·诺伊曼听完报告之后十分兴奋。他马上同希尔伯特和他的物理学助教诺德海姆（L.Nordheim）一起进行研究。在1926年冬天希尔伯特的讲演基础上，他们发表一篇论文，对于量子力学进行新的数学表述，而数学方面的工作主要是冯·诺伊曼做的。

冯·诺伊曼在量子力学方面的贡献绝不止于数学表述及解数学向题，他对量子力学本身有重要贡献，他引进纯态及混合态的概念，以及统计矩阵这个量子统计力学的主要工具。他支持玻尔等所倡导的哥本哈根解释，深入研究了测量过程，得出一些重要结论，如隐参数不存在。但是，这些准确结果由于不适当的引用而被误解，遭到一些不公正的批评。1932年，他出版了《量子力学的数学基础》一书，总结了他对量子力学数学基础的主要工作。本书是一部经典名著，曾被翻译成英、法、俄、日、西等语言出版。另外，他还对量子统计力学中遍历定理及H定理进行研究，这可说是他后来开辟遍历理论的先声。同时，他同维格纳一起对具体的物理向题进行研究。然而，使得冯·诺伊曼受到重视并且获得美国的聘任主要是由于他和维格纳的三篇论文。这三篇论文利用泡利的电子自旋和不相容原理解释了多电子体系的光谱线。其实群论已被数学家外尔等人引入物理学，但物理学家不喜欢这种抽象表述。冯·诺伊曼和维格纳的论文则解释了最基本的实验事实和过去可得到的一些经验公式，这让物理学家很佩服。从那时起数学在物理学中获得越来越多的应用。到20世纪30年代中冯·诺伊曼同约当（Pascual Jordan，1902—1980）、维格纳、小伯克霍夫（Garrett Birkhoff，1911—1996）一起，对量子力学的代数结构和逻辑结构进行系统研究，得到诸如约当代数的分支，以及量子逻辑一些新领域。维格纳评论说，单单冯·诺伊曼在量子力学方面的工作也足以保证他在当今的理论物理学方面占有卓越的地位，这的确可以说是历史的结论。

但是，在那时，大多数物理学家和数学家对冯·诺伊曼这一套并不理解。他们习惯于实实在在的具体的数学和物理，而希尔伯特空间则似乎又太玄乎了。传说希尔伯特本人曾问他年轻的学生：“你说说看到底什么是希尔伯特空间。”是的，无论是抽象代数还是抽象空间及其算子理论，思想上都渊源于希尔伯特。可是在20世纪20年代，这一套抽象玩意儿确实有些令人敬而远之，让人不是觉得数学一抽象就空洞得抓不着什么东西，就是觉得这些抽象数学表面上漂漂亮亮，实际上没什么大用，不必去管它。库朗和他的学生们就有这样的看法，算子理论能解微分方程吗？他们对此表示怀疑。可是几年之后，他们才慢慢看出这套东西的威力，觉得非学不可。到现在冯·诺伊曼所开创的一切已经成为经典，这些都显示出他的深邃的洞察力。

冯·诺伊曼不仅在数学上有深邃洞察力，对于世界事务、日常生活的见解也超过常人。1927年，他到柏林大学当无薪讲师，在柏林的两年成为他大丰收的时期，每年发表10篇论文。1929年，他到成立不久的汉堡大学当讲师。当时德国的大学的教授职位有一定数额，比如格丁根大学有4位数学教授、柏林大学有4位、汉堡大学有3位，他们不退休讲师就不能递补。冯·诺伊曼分析了当时的情形，他觉得三五年内，空缺的教授职位只有三四个，而竞争递补的讲师有60多人。虽说冯·诺伊曼在当时的工作足以使他出人头地，可是无论如何破格，25岁左右的年轻人就当正教授，也未免太过了。1929年年底，席卷全球的经济大萧条更增加了未来职位的不安定感。德国更是前景不妙，历史给像他这样的年轻犹太科学家规定了各种前途：要么留在德国受迫害甚至死在集中营，要么流亡到国外但是会为衣食操劳而使学术荒废。可是冯·诺伊曼比他所有同辈人都更为走运，他总是在最适当的时候在最适当的地方干最适当的工作：20世纪20年代他在世界的数学及物理学中心——德国，而20世纪30年代他在这个中心行将瓦解时，到了新的中心——美国的普林斯顿。

五、普林斯顿（1930—1938）

20世纪20年代，美国经济已居世界首位，科学发展却远比西欧落后。洛克菲勒搞一个基金会，一些有识之士开始用钱来请学者、名家到美国来讲学，当然定居更好。不过爱因斯坦、海森伯，他们都太留恋欧洲的学术环境了，不愿意来，也有来一阵又回去的。当时美国在聘请学者方面由康普顿（Arthur Holly Compton，1892—1962）负责物理学，维布仑（Oswald Veblen，1880—1960）负责数学，他们在科学研究上各有成就，在振兴美国科学上的功绩更是不可磨灭。由于埃伦费斯特的推荐，1929年10月维布仑向冯·诺伊曼发了聘书，请他到普林斯顿大学讲一个学期“量子理论”，一星期讲两三次。任期为1930年到1933年，每年一个学期，实际上早在1931年他已获得终身教授职位。同时也邀请了他的朋友维格纳。

现在看来，冯·诺伊曼是流亡科学家中最幸运的一位。他不仅及时逃脱了即将毁灭的德国科学圣地，同时又能极大地发挥其所长，直接推动他新的祖国登上世界的巅峰。究其原因，首先是他20多岁就出人头地，可是更重要的是，他遇到了伯乐——维布仑，还有一个在关键时刻提供的机会。1928—1929学年，普林斯顿大学聘请当时最伟大的数学家外尔讲数学物理学，即使从现在看，他也是最合适的人选，他在纯粹数学方面的知识广度几乎无人能与他相比，而且他对最时髦的物理学——相对论与量子力学给出了数学分析。遗憾的是，外尔的行事方式多少是老派欧洲人的风格，在关键时刻往往犹豫不决，错失良机。由于年近70岁的希尔伯特行将退休，而接班人也非外尔莫属，谁会为大西洋彼岸的当时绝非一流的美国大学放弃格丁根的职位呢？外尔第一次表示抱歉，他不能继续在普林斯顿教学了。对热衷于振兴美国数学的维布仑来说，这多少有点遗憾。他立即退而求其次，把毛头小伙冯·诺伊曼找来，同时搭配上维格纳。

到美国这个“机会的国土”闯一闯，激发了冯·诺伊曼的热情，况且当时为他提供的津贴一学期3000美元加上路费1000美元也确实不低（维纳当时一年工资共有4000美元）。冯·诺伊曼犹疑了一下，没立即答应。他当时还有一些私事要办，一是他父亲刚去世，他的母亲和兄弟希望他回布达佩斯接班，再就是，他准备结婚。过了几天，他从布达佩斯回信正式接受了普林斯顿大学的聘请，从此同美国结下不解之缘。

冯·诺伊曼的婚姻可谓门当户对。新娘是玛丽埃特·科维奇（Kovesi Mariette，1909—　），她祖父是房地产商，父亲是医学教授。她家的夏季别墅与冯·诺伊曼的比邻而居，因此两人从小认识。她处于社交界的中心，在一次巴黎旅游参观时，为冯·诺伊曼的博学所折服。她答应了冯·诺伊曼的求婚，并打算在1930年夏季成婚。由于冯·诺伊曼接受普林斯顿的聘书，因此，他们提前于1930年元旦完婚。不过，他们的婚姻并不和谐，冯·诺伊曼是工作狂，总是集中精力思考问题，对凡人琐事心不在焉，这让玛丽埃特觉得“没味”。这位有财产、独立而又自我的女性最终做出另一种选择。冯·诺伊曼的确想挽救这个婚姻，尽管他们的女儿玛琳娜（Marina von Neumann Whitman，1935—　）于1935年诞生，夫妻双方还是分手了，并于1937年正式离异。

玛琳娜是冯·诺伊曼唯一的孩子，继承了冯·诺伊曼的基因。她30多岁成了尼克松政府的经济顾问（首位女顾问），还当过通用汽车的总裁。据她在冯·诺伊曼的纪念会上讲，她的下一代也都十分出色。可世界何时能降生第二个冯·诺伊曼呢？

1930年，普林斯顿大学聘冯·诺伊曼当一学期讲师，第二年就升他为教授。以后几年，他每年都回到欧洲，那里的学术环境是美国所没有的。但是，他同后来的欧洲移民不同，他从生活上很喜欢美国的新环境：没有那么多陈规陋习，没有那么多条条框框，美国人比欧洲人热情友好，美国人相信竞争、相信技术，这也投合他的口味。他的新婚太太也非常喜欢美国，他们很快就能适应美国生活并扎下根。几乎没有欧洲学者能像他们那样，就连维格纳呆一段时间也嚷嚷受不了，要回去。冯·诺伊曼人缘很好，夫人又喜欢社交，他的家庭经常是大家聚会的中心，无论老年人、青年人都喜欢同他聊天。冯·诺伊曼从来没有大数学家的傲气，他头脑反应极快，但给人讲解时也很有耐心。

1930年，不仅是冯·诺伊曼生活上的转折点，也是他研究方向发生重要变化的一年。他在普林斯顿大学教了一学期量子力学之后，回到欧洲度假。1930年9月5日到7日在希尔伯特的故乡哥尼斯堡召开“经验科学的认识论”大会，第一天冯·诺伊曼做了关于形式主义的大会报告。形式主义是当时数学基础的三大派之一（数学基础三大派是罗素的逻辑主义、希尔伯特的形式主义与布劳威尔的直觉主义，其中形式主义与数学关连最为密切）。而真正引起1930年数理逻辑革命的是比冯·诺伊曼还年轻的哥德尔（Kurt Gödel，1906—1978）。哥德尔在第三天的会议上讲述了他的完全性定理。但是在私下，他也提到了他的第一个不完全性定理。所有听到此定理的大家对此都没有在意，而冯·诺伊曼立即意识到其划时代的重要性。不久，冯·诺伊曼得出了第二个不完全性定理，便写信告诉哥德尔。哥德尔回信说，他已经得出而且投了稿，于是冯·诺伊曼回信表示他自己就不再发表了。虽然，他与哥德尔对于不完全性定理的哲学解释意见相左，但他始终高看哥德尔。哥德尔没有冯·诺伊曼那么走运，第二次世界大战打起来之后，哥德尔离开纳粹统治的奥地利，冯·诺伊曼写信给维布仑极力推荐哥德尔到普林斯顿来。1940年，哥德尔到了普林斯顿高等研究院任研究员，但必须每年申请。

也是在1930年，一家美国著名的零售业（就像现在的沃尔玛，尽管没有那么有名）的两位犹太人老板想把他们的财产回馈给社会。他们原想用这些钱办所医学院，但被研究世界大学状况的费莱克斯纳（Abraham Flexner，1866—1959）劝阻。费莱克斯纳是位真正的爱国者，他看到了当时许多美国大学不怎么样。他认为，美国大学不是太少而是太烂，教师一周上13～14小时的课，没有工夫搞科研。于是他说服这两位有钱的慈善家建立高等研究院，而不是再建所医学院。这件事的成功最终改变了爱因斯坦的命运，改变了冯·诺伊曼的命运，也改变了美国科学的命运。顺便提一句，杨振宁、李政道获得诺贝尔奖的工作也是在这里完成的。

1933年1月召开会议确定高等研究院的人员组成时，冯·诺伊曼并没有获得通过。他太年轻了，又不是美国人。第一批教授有两位美国人——维布仑和亚历山大（James Alexander，1888—1971），两位德国人——爱因斯坦和外尔。其实这些都事先商量好了。没想到，就在希特勒上台前20天，外尔再次表示抱歉，辞去到手的教授职位，而留在格丁根。他不想离开德国。可是人算不如天算，谁能料到1933年1月30日，希特勒上台，从而改变了整个欧洲历史的进程呢！外尔就没有料到，他再一次错过了机会。幸运的是，这个机会落在了年轻的冯·诺伊曼头上。这样，外尔再一次为冯·诺伊曼提供了空缺，1933年9月普林斯顿高等研究院成立时，他成了教授，一直到1955年去华盛顿当官为止。

1933年，希特勒上台，大批德国科学家被迫离境，许多人到了美国。冯·诺伊曼当时就预言，要是这帮年轻人（指纳粹党徒）再掌两年权（很可能），他们就会把德国科学至少毁掉一代。9月，从他来时就筹建的高等研究院正式成立，这个研究院完全是仿照德国传统，专为著名学者从事他们的学术活动而建立的。50年来，它的确成为世界数学的中心之一。而第一批终身教授除了爱因斯坦、维布仑、亚历山大、冯·诺伊曼，另外还有莫尔斯（M.Morse，1892—1977），加上稍晚加入的外尔。外尔最终不得不于1934年9月来到这里，因为他的妻子是犹太人。冯·诺伊曼比他们年纪小得多，还不到30岁。他真算找到了最合适的工作环境了。

普林斯顿高等研究院显示当时美国科学的实况，也预示美国科学的未来。第一批教授3对3。3个外国人，3个美国人。3个美国人都是几何拓扑学家，代表着新兴的数学方向，但他们的地位远远不及这3个外国人。爱因斯坦不用说，外尔是继希尔伯特之后国际数学界的领袖人物。外尔应该是20世纪最伟大、最深刻的思想家之一。他不仅在数学上广博而深刻，而且在物理上真正开拓了新天地：

（1）外尔是规范场理论最早的提出者（1918），首先受到爱因斯坦的批评，其后又得到物理学家的理解。杨振宁和米尔斯在1954年再次提出后仍然未受到注意。一直到20世纪70年代，大家才恍然大悟，这个漂亮的规范场理论正好是基本粒子理论的基础。

（2）外尔和维格纳首先把群引入物理学中，物理学家视之为瘟疫，称为群的瘟疫，避之唯恐不及。20世纪40年代之后，物理学家才认识到群论的重要性，群论成为人人都要学的功课。从70年代初起，一年至少开一次群在物理学中的应用的国际研讨会。外尔的书太难懂了，然而万变不离其宗，至今外尔所发展的群论仍然是物理学家研究原子及分子物理学、核物理学，以及基本粒子物理学的不可或缺的工具。无怪乎维格纳说：“数学有着不可思议的有效性。”

外尔在数学界的地位就像爱因斯坦在物理学的地位一样，在美国他写了“半个世纪的数学”显示出他的教父形象，他的《对称》更是显示出他对欧洲文化的精通。不过，外尔并不像冯·诺伊曼一样把美国作为第三故乡，也不发表政治方面的意见。二战结束后不久，他就回到瑞士这第二故乡，最后在这里去世。

冯·诺伊曼则不大相同，1937年获得美国国籍之后，成为一位真正的爱国者。在美国的最初十年除了继续在德国开始的工作之外，他又开辟许多新方向，其中特别重要的是遍历理论、拓扑群理论和算子代数理论。

20世纪30年代初，冯·诺伊曼对拓扑群理论作出了卓越贡献。1933年他对紧致群的研究解决了著名的希尔伯特第五问题。

早在1929年，冯·诺伊曼开始算子代数的研究。这方面的研究深受两方面的影响，一方面是爱米·诺特（E.Noether，1882—1935）及阿廷（E.Artin，1898—1962）在20年代后半期关于环论研究的著名工作的影响。另一方面是为量子力学奠定数学基础的必然需要。这样，冯·诺伊曼创立了算子代数这门新的分支。他去世之后，为了纪念他，人们把他首先研究的算子代数（他称为算子环）称为冯·诺伊曼代数。

冯·诺伊曼在纯粹数学方面的工作非常广博，他在当选为美国国家科学院院士时，谈起自己的工作，他认为量子力学的数学基础、遍历理论、算子环理论是他最好的工作。但实际上，他在数学的各个方面都有卓越的贡献。当然，他比20世纪最大的数学家庞加莱、希尔伯特、外尔在广度上稍有逊色，因为他在数论、代数拓扑学、代数几何学、微分几何学等当前热门领域没有做过重要工作。即便如此，他在纯粹数学领域，仍远远超过大多数同时代数学家。无论从什么角度，他都可以跻入20世纪十来位最大的数学家之列。如果仅考虑应用数学，应该说他是超群绝伦的。要知道，20世纪数学门类繁多、内容复杂，一个人在某一狭窄分支能作出一些贡献就已经不错了。

冯·诺伊曼在纯粹数学方面的工作有其显著的特点，他对现代数学的结构有着明确的认识，善于把复杂的结构分解成为各个组成部分进行分析。他能够把复杂的对象加以系统化、公理化，这反映他能透过纷乱复杂的关系认识到事物的本质的洞察力。

正是由于他佩服哥德尔对数学基础进行的革命性的变革，他完全放弃了已进行了十年的数学基础的研究。当哥德尔长期受到某些人阻拦而不能成为高等研究院终身教授时，他总是打抱不平说：“连我们都是，可是这位亚里士多德以后最伟大的逻辑学家却不是。”1937年，另一位伟大的逻辑学家图灵（Alan Turing，1912—1954）应邀到普林斯顿访问，冯·诺伊曼想让图灵当他的助手，但图灵没有答应。

冯·诺伊曼同大多数美国数学家关系不错，比如他同维纳关系颇好。1937年春夏之交，维纳在马里兰州约翰·霍普金斯大学讲演后，回麻省理工学院途中在冯·诺伊曼家呆了四天。两个人对数学进行了多方面的讨论，特别讨论了他们都感兴趣的统计力学及遍历理论。由于维纳严格吃素，于是冯·诺伊曼的夫人绞尽脑汁地给他准备丰盛的素餐，这让维纳感到很高兴。他同冯·诺伊曼谈到了他和布什（Vannevar Bush，1890—1974）一起研究的计算机，还谈到一年之前在清华大学的经历。冯·诺伊曼对中国也产生了兴趣，维纳十分热心地为他搭桥，他马上给李郁荣写信，介绍冯·诺伊曼是当今世界上数一数二的数学家、没有国家及种族偏见，他有钱不在乎薪水，够花就成，而且喜欢接近年轻学生，没什么架子。结果却由于芦沟桥事变使冯·诺伊曼难以成行。

冯·诺伊曼没来成中国，波兰的数学家巴拿赫（S.Banach，1892—1945）等人以及要在美国逗留的乌拉姆（S.M.Ulam，1909—1984）邀请他到波兰的里沃夫去讲学。1937年夏天，冯·诺伊曼到波兰呆了几天，他很喜欢波兰数学家在咖啡馆里自由自在地讨论数学的情景。他们在一起愉快地讨论许多问题。当时里沃夫是泛函分析的一个中心，但不久法西斯德国入侵把这一切都化为乌有。

同在1937年，冯·诺伊曼自己也遇到不愉快的事。他的夫人带着两岁的女儿离开他，嫁给一位实验物理学家。1938年夏天，他回请乌拉姆到布达佩斯来玩，他们在一家大餐馆边吃边聊，冯·诺伊曼之前很喜欢开玩笑，过去常常讲，“我好多想法都是因为夫人坐在旁边才想到的”，现在他也没有那份兴致了。这时，他们看见一位打扮入时的女人走过，冯·诺伊曼就去同她搭话。她离开后，冯·诺伊曼说，这是位老相识，最近要离婚了。乌拉姆就说，为什么你不娶她呢？也许这话启发了冯·诺伊曼，他留下来帮她办妥离婚手续，并同她在布达佩斯结婚。过了一年，这位新夫人克拉拉·丹（Klara Dan，　—1963）移居普林斯顿，他们的家又成为学者们经常聚会的地方。克拉拉是冯·诺伊曼的贤内助，也是首位计算机程序员。

六、第二次世界大战（1939—1945）

冯·诺伊曼这代人和他前一两代人都经历了两次世界大战，第二次世界大战尤为惨烈。第一次世界大战其实是不期而至，很多人都以为会速战速决。冯·诺伊曼一家在匈牙利实际上没受到多大影响。对于第二次世界大战，不少人都预见到了。冯·诺伊曼更是预测将在1938年打起来。结果由于英国首相张伯伦（Authur Neville Champerlain，1869—1940）的绥靖政策，推迟了一年，1939年9月1日德国进攻波兰，而美国到1941年12月珍珠港事变后才参战。

冯·诺伊曼在普林斯顿的安乐窝中从来也没有忘掉周围的世界。他懂得历史，对世界局势有着明确的分析。1935年底，波兰年轻数学家乌拉姆到普林斯顿找冯·诺伊曼，他正在同另一位数学家谈政治。冯·诺伊曼对局势很悲观，他觉得战争不可避免。他还看出来苏联是德国的主要对手。乌拉姆对马其诺防线印象很深，就问：“那法国呢？”冯·诺伊曼回答：“法国不顶事。”时过境迁，谁那么早就对五年后的事情这么了如指掌了呢？

在第二次世界大战爆发时，冯·诺伊曼的研究方向有一个大转弯。如果说在这之前，他的工作主要是纯粹数学，那么这之后，他主要搞的是应用数学。这不能不说是20世纪新型数学家的一个重要特点。作为20世纪天才的数学家，他和维纳都从纯粹数学走向应用数学，从而比他们前辈数学家发挥出更直接的社会作用。在1941年前，他仍然继续在算子代数方面的工作，但注意力已转向流体力学，他在这期间最重要的工作无疑是创立博弈论。他在1940年到1941年间为博弈论（又称对策论、竞赛论）所做的奠基性工作实际上是1928年他证明的“极小极大定理”的继续。20世纪30年代，他对数理经济学有本质的发展。这次他应用了布劳威尔（Luitzen Egbertus Jan Brouwer，1881—1966）不动点定理。这是不动点定理第一次在经济理论上的应用。其后不动点理论和数理经济学都获得大发展，到50年代，数理经济学家几乎没有不懂得不动点定理的了。

1940年，冯·诺伊曼深深感到有必要深入研究博弈论。世界充满了斗争和对抗，无论是军事上、政治上、经济上甚至生活中都莫不如此。他用自己的分析把这种复杂的现象变成一个系统的理论，并对经济进行分析。他同摩根斯顿（Oscar Morgenstern，1902—1977）合作的《博弈论与经济行为》于1944年出版。这部600多页的巨著是博弈论也是数理经济学的经典著作。它还开辟了应用数学的一大新方向——离散数学的应用，而过去数学的应用一直只是分析数学（连续数学）的应用。

冯·诺伊曼当然也没有忽视对分析数学的应用。无论是飞机设计还是爆炸乃至气象预报，都离不开流体力学。早在20世纪30年代中期，他就对湍流等问题感兴趣。他深深认识到，流体力学方程组是非线性方程，而当时的解析方法对解非线性方程是无能为力的，甚至定性的结果也得不出。当时他就已经考虑到利用数值方法的必要性，通过快速的数值运算，可以对未来的理论提供丰富的启示，进而提出令人满意的理论。由于计算量庞大，在没有电子计算机的情况下，这一切想法还是无法实现的。不过他在40年代初已经进行了多方面的理论研究，并且参与许多军事方面的研究。1940年就担任陆军阿伯丁试验场弹道实验室顾问。

1941年12月珍珠港事变，美国参战之后，冯·诺伊曼积极投入军事项目的研究。1943年，他冒着极大危险去英国研究流体力学。他涉及的最为重要的两大事业是制造原子弹和研发计算机，并一直进行到战后。这两项事业后来对整个世界都产生了极其重大的影响，而在当时，几乎没什么人能意识到。

七、制造原子弹（1943—1952）

20世纪最重要的两项“成就”无疑是原子弹及电子计算机，而亲自参加两者研究并作出巨大贡献的也许只有数学家冯·诺伊曼一人。

比较起来，制造计算机的想法不是什么了不起的创新，然而释放原子能或制造原子弹一直到20世纪30年代都没什么人有把握，其中许多人决不是凡夫俗子，而是在实现原子弹爆炸的思想之链上的一些顶尖科学家。从历史上看，10年就从无到有造出许多人连想也不敢想的原子弹和氢弹，这种创造力大概只有上帝造人的奇迹可比。

一切都在1895年到1945年这短短50年间发生。现在很多人都想制造核武器，这对他们来说很容易，可是凡事开头难，许多“第一次”的困难早已被克服，地球上的核弹数目已经足够毁灭地球几十次。

解决这个过去极难现在变得如此容易的问题经过了十大关键步骤。值得一提的是，匈牙利的犹太四人帮（齐拉、维格纳、特勒、冯·诺伊曼）也许起着重大作用。

1．原子不是不可分的。古典原子论认为，原子是不可分的。1896年放射性的发现从根本上动摇了原子不可分的假设，谁动摇的？居里夫人？放射性发现以后，的确有人想利用放射能，但这个放射能其实不好利用。在历史上，这其实是一个弯路。

2．质能公式。1905年，爱因斯坦建立了狭义相对论，其中一个推论就是质能公式：

E＝mc²

这是一个纯理论的成就，当时也不太可能进行实验验证。然而它是一切核武器的基础。不过就连爱因斯坦也不相信他的公式这么厉害，他曾表示根本无法从物质中提取能量。

3．原子的结构。原子既然可分，就得想象原子的模型。卢瑟福（Ernest Rutherford，1871—1937）证明原子有带正电的核以及质子的存在。他还在1920年猜想中子的存在。

4．中子的存在。1932年英国物理学家查德维克（James Chadwick，1891—1974）发现了中子，这样，轰击原子才有了更好的炮弹。原子裂变才有可能。

5．链式反应。1933年匈牙利物理学家齐拉（Szilard）猜想用一个中子轰击原子核，如果能产生两个或两个以上的中子，则可形成链式反应。

6．用中子轰击原子。有了中子以后，意大利物理学家费米就按照周期表的顺序用中子一个一个地轰击原子，用中子轰击铀时，他以为他发现了“超铀元素”，并因此荣获1938年诺贝尔物理学奖。这个错误的喜剧改变了他自己的命运，也改变了世界的命运。他在1938年12月领奖以后，就带着他的犹太裔妻子劳拉·费米跑到美国，从此成为制造原子弹的核心人物。

7．发现原子核裂变。就在费米跑到美国去时，德国物理学家哈恩（Otto Hahn，1879—1968）等人用慢中子导致铀裂变，同时发现放出中子，并寻求正确的解释。玻尔等人研究了裂变机制，指出慢中子可引起超铀235裂变，预言钚239可裂变。

8．实现可控核裂变。1942年12月费米成功建成世界上第一个核裂变反应堆。其中需要解决的主要技术问题有两个：一个是分离出足够多的裂变物质，例如铀235。至今已发明很多种方法，如离心法，气体扩散法，电磁法。这也是当前许多打算成为核国家的国家所碰到的一个问题。另一个是证明中子慢下来变得可调节，例如用重水，石墨等。

9．爆弹设计。理论上把两块相当纯度的铀235碰在一起超过临界体积就可以产生自持续的链式反应。但是如何设计，如何引爆就是数学家的问题。冯·诺伊曼在其中起了决定性作用。其实当时有许多理论问题：能不能爆炸？爆炸威力有多大？爆炸威力要是比普通炸弹增加不了太多，当然也没太大用。后来证明，它比普通炸弹大千倍以上。

10．氢弹。原子弹成功之后，氢弹还是没谱。当时不知道氢弹是否当量太大会把整个大气点燃？首要的技术问题则是如何引爆？1943年，冯·诺伊曼参与洛斯·阿拉莫斯的曼哈顿计划，受到唱主角的物理学家的欢迎。他同奥本海默（Robert Oppenheimer，1904—1967）、费米、特勒等人的关系都不错，维格纳更是他的老朋友。他们认为冯·诺伊曼不仅是位全面的天才，预言家，而且是解决问题的能手。过去冯·诺伊曼是以搞纯粹数学而闻名，可是他对数学分析乃至数字计算十分熟练。他对当时遇到的主要困难——如何引爆原子弹提出自己的建议，结果被实验所证实。他还对提高原子弹的爆炸效果以及有效地配置原料进行估计。这些在当时都是十分关键的。他比一般数学家更能同物理学家进行交流，懂得他们的具体技术细节，并能马上转化成数学问题。甚至领导曼哈顿计划的军人格罗夫斯也喜欢在战术问题上同冯·诺伊曼讨论，因为他的头脑并不只是限于解决一两个局部问题的。

在洛斯·阿拉莫斯，工作非常紧张，冯·诺伊曼的工作常常是进行无止无休的讨论，许多人在黑板上，在纸上进行复杂的推演和计算，冯·诺伊曼却总是在头脑里进行，往往很快就能得出结论。科学家在工作之余有时打扑克来松弛一下神经，冯·诺伊曼也喜欢玩，但是这位博弈论的开创者却常常输钱。有位数学家兴高采烈地谈起他如何如何赢了冯·诺伊曼10美元，他知道冯·诺伊曼写了《博弈论与经济行为》，于是花了5美元买下这本书，而把另外5美元贴在封面里头作为战胜这位博弈论专家的标志！

爱因斯坦极力倡导和平主义，倡导原子弹公开，倡导世界政府，愿望虽好，就是在苏、美两边都不讨好。冯·诺伊曼的预言经常十分准确，他早就说过，苏联肯定要制造原子弹，而且肯定很快就会造出来，果然苏联在1949年9月已经造出来了。他的确说过，乘苏联还没有造出来，要进行先发制人的打击。不过杜鲁门政府一直想通过政治解决，没敢怎么干。其实，早在原子弹投下之后，洛斯·阿拉莫斯大都人去楼空，但还是有少数人一心想发展氢弹（当时称超级炸弹），最坚持而且取得最后成果的是特勒。不过在当时，除了冯·诺伊曼等几个人之外，没人支持，大多数人反对，尽管他们反对的理由不同。多数人从道德上讲，反对这种大规模杀伤性武器，也有少数科学家出于技术理由反对，也就是做不成，没有可行性，两位顶尖科学家费米和贝特（Hans Bethe，1906—2005）就是如此。更为有意思的是，即便1950年1月杜鲁门总统正式宣布研制氢弹之后，核心组成员还有唱反调的人。反调并非没有道理，冯·诺伊曼说，特勒的10个立意，9个都是错的，第十个可能还有可取之处。1952年初，数学家乌拉姆突破如何由原子弹来点燃氢弹这个困难，冯·诺伊曼用他的计算机验证了可行性，最终这个当时只有4个人赞成的方案获得通过。下面的路就一马平川了。1952年9月美国的氢弹试爆成功，特勒因此而获得氢弹之父的美名。不过，正如大家所说，制造氢弹的六步中，特勒完成了五步半，关键的半步得归功于数学家。

八、研发计算机（1944—1955）

尽管冯·诺伊曼在原子弹的研制方面有重要贡献，但究竟是个配角。一个偶然的机会把他引向20世纪后半期最重要的科学与技术——研究电子计算机。在这一领域他再一次发挥独创精神，成为计算机科学、计算机技术、数值分析的开创者之一。

1944年夏天，哥德斯坦（Herman Goldstine，1913—2004）从阿伯丁医院出来到火车站等去费城的火车，正巧碰上了冯·诺伊曼。哥德斯坦早就听说过这个世界闻名的大数学家。他怀着年轻人会见大人物那种惴惴不安的心情走近冯·诺伊曼作自我介绍，开始攀谈起来。冯·诺伊曼热情友好，毫无架子，很快就使他不觉得拘束，大胆地谈起自己的工作来。当冯·诺伊曼知道他正在搞每秒能算333次乘法的电子计算机时，谈话气氛一下子变了。冯·诺伊曼严肃而认真地询问，使哥德斯坦觉得好像又经历一次博士论文答辩。当然，冯·诺伊曼从中看到了具有头等重要意义的大事。

早在第一次世界大战时期，美国已有马里兰州、阿伯丁试验场的弹道实验室研究火炮的弹道计算。这是武器研发最重要的课题之一。缺少的就是能快速处理大量数据的计算机。1943年以前，受阿伯丁试验场弹道实验室的委托，建造第一台电子计算机的工作正式在费城宾夕法尼亚大学莫尔学院上马。这就是“电子数字积分计算器”（简称ENIAC）。主要研制者是工程师艾克特（J.P.Eckert，1919—1995）及物理学家莫克莱（J.Mauchly，1907—1980）。冯·诺伊曼急不可耐地想要看看这台尚未出世的机器。他很快就得到同意。艾克特说，他能够从冯·诺伊曼提的第一个问题来判断他是否是位真正的天才。1948年8月初，冯·诺伊曼来了，他一看就问起机器的逻辑结构，而这正是艾克特所谓天才的标志。从那时起，冯·诺伊曼就成为莫尔学院的常客了。他同ENIAC的首批研制者们进行认真而活跃的讨论，问题集中在ENIAC的不足之处。他们考虑研制一台新机器电子离散变量自动计算机（EDVAC）。

1945年3月，冯·诺伊曼起草EDVAC设计报告初稿，其中已有计算机与神经系统的对比，这为后来自动机研究埋下伏笔。这份报告对后来的计算机影响很大，其中主要确定计算机由计算器、控制器、存储器、输入、输出五部分组成，介绍了采用存储程序以及二进制的思想。虽然冯·诺伊曼的参与开辟了电子计算机的新时代，但这台机器却长期停留在纸面上。一直到1952年才正式建成。到此时，存储程序计算机已经造出不少台了。原来到1945年底，ENIAC完成之后，研制人员就因为优先权问题而争吵起来，莫尔学院的研制小组于是陷于分裂。两位技术专家艾克特和莫克莱自己开公司，从事计算机研制及大规模生产。而冯·诺伊曼，哥德斯坦等回到普林斯顿高等研究院，开始新一轮合作。

九、战后（1945—1957）

1946年初，普林斯顿高等研究院由于冯·诺伊曼的归来而热闹起来。在他的影响下，这所原来因从事理论研究而显得很冷清的单位，开展了从计算机的研制到计算机应用的广泛研究。他们建立实验室，请工程师及各种专业人员，形成一个真正的“计算机研究热”。这对计算机的普及影响很大。这种热潮继续了十年左右，由于冯·诺伊曼去华盛顿及哥德斯坦离开，高等研究院恢复了原先的老样子。

在各方的资助下，冯·诺伊曼等首先研制“完全自动通用数字电子计算机”，它以高等研究院的缩写IAS命名，是现代通用机的原型。1946年6月，冯·诺伊曼的《电子计算装置逻辑结构初步讨论》发表。IAS在1951年夏交付使用，效率比ENIAC快几百倍。

显然，冯·诺伊曼脑子里面不完全是技术问题，他念念不忘的是使用计算机，尤其是应用计算机去解复杂的数学问题。他必须在两方面取得进展：一是如何使编程序变得又快又好，一是怎样把数学问题进行数值计算。他对两方面都作出了贡献。

40年代中期，冯·诺伊曼集中进行自动机理论的研究，到50年代中期，自动机理论成为计算机科学中一个非常活跃的分支。

1948年9月，冯·诺伊曼在希克松会议上公布自动机研究工作成果，并于1951年发表，题为《自动化的一般逻辑理论》。他特别感兴趣的是复杂自动机，像人的神经系统及大型计算机。在后来的研究中他对于由不可靠元件如何组成可靠的生物体感兴趣。1952年秋天他开始研究自动机的自复制问题，他设计了一个具有29个态的自复制系统。这些手稿一直到1966年才公之于世。临终前，他深入比较了天然自动机和人工自动机，没有完成的手稿在1958年以《计算机与人脑》出版。

由于冯·诺伊曼在战时的杰出工作，战后，他被授予总统亲自颁发的功勋奖章，以及海军颁发的杰出文职服务奖。

十、参与政治

对于一般的学者，也许只对他的学术成就稍加评述就够了，而对于冯·诺伊曼，这样做就未免有失偏颇。不少人对冯·诺伊曼的政治态度与道德取向有种种非议，然而，只有搞清楚事实并对其影响做出分析才是全面认识他的正确途径。大多数数学家对社会历史进程影响不大，的确也有个别的数学家当上部长或总理，可是，恐怕没有人像冯·诺伊曼那样实实在在地影响第二次世界大战后的历史进程。

第二次世界大战后，人类进入了一个新时期，历史上称为冷战时期。冷战时期的主要特点是以美国和苏联为首的两大阵营对峙。从军事技术上来讲，发展核武器和运载工具已成当务之急。双方都认识到，军备竞赛的基础是科学和技术，科学已从战前的小科学发展成建立在国家实力基础上的大科学。比起核武器，由维纳和冯·诺伊曼等人所发展起来的计算机科学技术、控制论、信息论似乎还不那么受到重视，它们仍然只不过是军备竞赛的工具。

战后，科学家的形象发生很大变化。社会普遍认识到他们的重要性，但广岛投下的原子弹也让多数人感到震惊和恐惧。政治仍然掌握在政治家手中，将军与科学家也起着或多或少的作用。在东方阵营中，当然是斯大林说了算，而在西方，美国总统杜鲁门看来不是他的对手，可是他下面有一套机构为他出谋划策，其中包括政府部门，如1947年成立的中央情报局，参谋长联席会议，以及三军的科研管理机构。除了政府机构之外，还有企业及民间的智库，如IBM，以及兰德（Rand）公司。有意思的是，1948年，它们不约而同地聘请同一个人当它们的顾问，这就是冯·诺伊曼。那一年，他担任6个政府、军事部门的顾问，同时又兼任6个民间智库的顾问。这种情况可谓空前绝后。

冯·诺伊曼能够获得这种地位，无非是两条：政治上可靠，事业上能干，用中国人的话来讲就是“又红又专”。当然，首先是红。这方面，冯·诺伊曼没问题，遗憾的是，他站在众多数学家的对立面上，并因此遭人诟病。

第二次世界大战以后，很多问题摆在人们特别是权势人物及科学家面前：要和平还是安全，继续发展核武器、改进原子弹还是停止发展，对苏联强硬还是妥协。对这些问题的回答把美国人分化为鹰派和鸽派。冯·诺伊曼的态度十分明确，他属于鹰派，不过比起特勒等人来，他只能算鹰派中的鸽派。

为什么说冯·诺伊曼是鹰派中的鸽派呢？原来大清洗并非斯大林的专利，就在冷战的关键时刻，美国也掀起一场大抓“反革命”的运动，这就是臭名昭著的麦卡锡主义。

麦卡锡主义是美国参议员麦卡锡（John McCarthy，1908—1957）在1950年初提出来的。他利用了美国人民希望有安全感而又不想打仗的心理，搧起反苏、反共的狂潮。这与1949年发生的几件事有关。首先是中华人民共和国成立，一边倒，倒向苏联。其次，苏联试验原子弹成功。再有柏林危机的出现，还有曼哈顿计划中苏联间谍被揭露。这些再加上党派政治的因素，使得麦卡锡攻击美国政府甚至军队中都有内奸的渗透，他还开出“黑名单”，准备大抓间谍，同时对于像爱因斯坦等自由派和平人士也加强监督与控制。就是像冯·诺伊曼这样的鹰派，也会有人提出各种质疑。这时首当其冲的是奥本海默，他是曼哈顿计划的总负责人。由于他过去与共产党有染，加上出了几个苏联间谍，自然脱不了干系。当然，也少不了极端分子给扣帽子、打棍子，特勒就是一个，他对奥本海默不支持氢弹研制耿耿于怀，指称奥本海默不可靠。轮到冯·诺伊曼作证时，他虽然在发表氢弹问题上与奥本海默有不同看法，但认为奥本海默在政治上还是忠诚可靠的。当反对研制氢弹的奥本海默对美国的忠诚受到怀疑时，冯·诺伊曼曾替他辩护。最终奥本海默未被起诉。

大战结束后，大多数科学家很快就摆脱军事研究，回到他们的老行当上，过着自由自在的生活。很多人对于投放原子弹的后果感到震惊。冯·诺伊曼一开始就同这些科学家不同，他投书《纽约时报》极力为核试验辩解。他甚至主张对苏进行预防性战争，可以说是十足的“鹰派”。

冯·诺伊曼战后的军事研究主要是研制氢弹。在原子弹还没有试爆时，被称为“氢弹之父”的特勒（Edward Teller，1908—2004）已经在设计制造氢弹的方案。战争结束后，许多人为这种大规模杀伤性武器感到震惊，极力反对这种当量再增6个数量级的超级炸弹，其中典型代表是曼哈顿计划的领导人——奥本海默。在多数人的反对下，氢弹计划只好暂停。由于苏联在1949年原子弹试爆成功，杜鲁门才在1950年1月重开氢弹计划，冯·诺伊曼也是其中主要顾问。最后1952年氢弹试爆成功。

与此同时，冯·诺伊曼的公职头衔达到十几项，他不仅是陆军、海军、空军各机构的顾问，而且是政府一些高级机构的成员（统领美国原子能研究的机构，后来称为原子能委员会。）。1952年，冯·诺伊曼正式成为由总统任命的原子能委员会总顾问委员会成员。1955年被艾森豪威尔总统任命为国家原子能委员会委员，同时还是导弹顾问委员会主席。作为一个高级行政官员，他迁往华盛顿居住。

数学界也没有忘掉他，战后各种荣誉、头衔纷至沓来，1951到1952年，他担任美国数学学会的主席。费米和爱因斯坦相继在1954年和1955年去世，而刚过50岁的冯·诺伊曼这时也已疾病缠身了。1955年夏天，他觉得胳膊抬不起来，动了手术之后发现得了骨癌。这显然是放射性作用的结果。他那理智的头脑知道自己没有多少时间了，他坚持工作，甚至运动，但疾病很快地恶化。他只能在轮椅上呆着，但他还是不停地思考、写作甚至参加会议。1956年，他被授予总统颁发的自由奖章，同年，又荣获爱因斯坦纪念奖章与费米奖章。1956年4月，他被送到瓦尔特·里德（Walter Reed）医院，虽然他与那不可避免的命运拼搏，但始终无法同病魔抗衡，留下大量未竟之业于1957年2月8日与世长辞，后葬在普林斯顿。

工　　作

冯·诺伊曼是20世纪最伟大的数学家。他的贡献遍及许多领域，我们可以归纳为四大彼此相关的部分：纯粹数学、应用数学、博弈论（对策论）及计算机科学。

冯·诺伊曼在纯粹数学、应用数学上作出了多方面的贡献，他创立了对策论（博弈论），发展了数理经济学。他广为人知的贡献是关于电子计算机的设计、技术、应用及理论发展，他的思想直接影响计算机的体系结构设计，以致现在的计算机称为冯·诺伊曼型计算机。二进制输入输出、程序内存乃至并行计算机、软件设计一些思想也来自于他。他视野广阔、高瞻远瞩，不只把自己局限在计算机的设计及制造上，而是同时关注其在各方面的应用。其中最重要的就是直接参与首次数值天气预报。为了有效使用计算机，他开创了数值分析，设计和改进许多算法（最突出的是蒙特卡罗方法）。在关注计算机科学、技术及应用的同时，他还前瞻性地开创了自动机理论，《计算机与人脑》就是这个理论的有机组成部分。

一、纯粹数学

19世纪末纯粹数学形成四大领域、四小领域。四大领域是数论、几何、代数、分析；四小领域是代数数论、代数几何、微分几何、李群理论。到20世纪，四小领域取得巨大进展，它们同时也推动20世纪新数学特别是结构数学的产生。按照布尔巴基的说法，数学研究的基础结构、有序结构、代数结构及拓扑结构，对这些结构的研究形成了抽象代数学、格论、一般拓扑学，外加测度论，冯·诺伊曼在这些领域都做过贡献。在此基础上形成代数拓扑学、微分拓扑学、泛函分析、大范围分析等，但只有泛函分析才是冯·诺伊曼的强项。

归根结底，冯·诺伊曼是位数学家，他在纯粹数学和应用数学方面都做了大量工作，如数学基础——集合论、代数学（连续群）、格论、测度论、算子理论等。他的许多著作大都已成为各领域的经典著作，特别是最近成为大热门的算子代数，则是冯·诺伊曼的独创，他理所当然应被称为“算子代数之父”。而从历史上看，数理逻辑和遍历理论也具有相当的重要性。由于他在纯粹数学方面博大精深，1937年，美国数学会授予他波谢（Bôcher）奖（这个奖是美国数学界最高荣誉之一，之前只有维纳等五人获奖）。

1．数理逻辑

20世纪初的新兴数学一个是结构数学，一个是数理逻辑。它们的数学基础是什么？无疑是康托尔的集合论，没有集合论就没有当时的新数学。尽管康托尔奠定了集合论的基础，却遗留下一些矛盾和问题谧然长逝。由此出现数学基础论的危机。集合论主要是无穷的理论，基本概念无疑是基数和序数。基数就是1，2，3，4等，序数就是第一，第二，第三，第四等，问题是把它们推广到无穷并不简单。康托尔本人花了很大力气，得到了许多无穷（即超限）基数和序数，但他始终没有得到一个合适的定义。

冯·诺伊曼在大学时期已经开始研究这些基本问题，并作出两大基本贡献：一是定义超穷序数，二是开创新的集合论公理系统。他在文章《超穷序数引论》一开始就声称：“本文的目的是，精确而具体地理解康托尔的序数概念。”他认为康托尔本人的定义是对集合的类的共同性质的“抽象”，这个定义有点含糊，而冯·诺伊曼则给出一个明确的定义：每个序数是以前序数的集合。他的这个定义清楚明确毫不含糊，现在已成为标准的定义。

当时已有策梅洛提出，费兰克尔修改的集合论公理系统ZF（以这两为数学家的姓的首个字母来缩写表示），冯·诺伊曼则提出自己的系统，后来发展成NGB系统［以冯·诺伊曼、哥德尔，贝耐斯（Bernays，Paul，1888—1977）的姓首字母来缩写表示］。1923年8月15日他给策梅洛寄去自己的论文，他表示他的公理系统有如下的特点：①集合是由函数及变元等原始概念得出，②弗兰克尔的“代换公理”采用加强的形式，③容许“充分大”的集体，但不容许它们是任何集合的元素。

NGB系统是1938年哥德尔关于连续统假设协调性证明的基础。

2．算子理论及算子代数

希尔伯特空间的算子理论是泛函分析的核心之一。它来自冯·诺伊曼的综合及发展，而算子代数（冯·诺伊曼称为算子环）则是冯·诺伊曼的首创。他还进一步把它发展成连续几何、量子逻辑等理论。

冯·诺伊曼对算子理论研究的出发点是为量子力学奠定数学基础，他的主要贡献在于引进希尔伯特空间抽象概念并给出公理化定义，并系统建立希尔伯特空间的算子谱理论，特别是对无界埃尔米特算子理论进行研究。

当时海森伯用的是无穷阶矩阵作用到无穷维向量空间上，而薛定谔用的是薛定谔方程，即微分算子作用到波函数上。数学家早就研究过这些对象，19世纪末已经研究过无穷阶矩阵，希尔伯特在1906年引进l²空间，也就是平方可和空间的概念，它是n维欧几里得空间的推广。同时数学家也知道由平方可积的函数构成的空间L²，而波函数的概率解释也要求Ψ属于L²。1907年两位数学家证明l²空间与L²空间是等价的，两者是同一种空间的两种不同表现形式。这种等价性不正是从数学上反映海森伯的矩阵力学和薛定谔的波动力学的等价性吗？！剩下的问题就是把它们公理化，冯·诺伊曼把它们命名为希尔伯特空间。这是泛函分析最基本的概念，也是量子力学的理想的数学表述的工具。

希尔伯特空间是欧几里得空间到无穷维的推广，欧几里得空间的线性变换（矩阵）也就自然推广成希尔伯特空间的线性算子，而线性变换的特征值（本征值）也就自然推广成线性算子的“谱”。有趣的是，希尔伯特在1910年定义他的“谱”时，万万没有想到它们居然对应着原子光谱。当时他研究的是比较窄的一类积分算子，不久又把这种谱理论推广到更广泛的一类算子，用冯·诺伊曼的话讲，就是希尔伯特空间的有界（对称）线性算子。冯·诺伊曼把量子力学公理化时，用希尔伯特空间的点表示物理系统的状态，物理系统的可观测量则由希尔伯特空间的线性算子来表示，而能量算子的本征值和本值函数就是该系统的能级及相应的定态。冯·诺伊曼在数学及物理学之间建立的这种对应关系简直漂亮极了，使人觉得这不是凡人的作品。

遗憾的是，物理学中碰到的算子一般不是有界的，冯·诺伊曼必须努力从数学上把希尔伯特的谱理论推广到无界厄米算子上。正是通过这种努力，他建立了算子理论这门崭新的学科。他选取最一般的有谱分解的厄米算子——超极大对称算子来建立他的谱理论，从而使这个问题得到圆满解决，这是1929年的事。

冯·诺伊曼研究算子代数的出发点是研究量子力学，经典物理学中的物理量用数表示，而量子力学中的物理量则对应于希尔伯特空间的算符，即数学家的算子，也就是作用于函数上产生另外一个函数的运算，如微分算子。一组算子满足代数的公理，加上一些其他条件就构成算子代数，现在称为冯·诺伊曼代数，冯·诺伊曼等人不仅首先引进它，还把构成代数的因子分成三型五类，对I型完全分类，而Ⅱ型、Ⅲ型分类只获得局部结果。

算子代数的奠基性工作是由冯·诺伊曼和他的学生马瑞（F.J.Murray，1911—1996）在1936年到1943年发表的四篇论文“算子环Ⅰ、Ⅱ、Ⅲ、Ⅳ”，全文达800页之多。在第一篇文章中，他列举研究的动机有下列几方面：①给算子演算一个框架，②把酉表示理论从经典的限制中解放出来（从有限维表示过渡到无穷维表示），③为量子力学提供数学工具，④建立不满足有限性条件的抽象代数学。

经过他们的研究，算子代数已经成为现在数学分析中的热门，而且在物理方面（尤其是量子场论）有着重要的影响。

算子代数是代数结构与拓扑结构相结合的产物，所以它的结果往往显示代数的形式，而证明却用解析的方法。在研究中，有限维代数的结果是研究者的指路明灯。有限维代数可以分解为两大类，可解代数和半单代数，其中半单代数又可以分解为单代数的直和，而每一种单代数又可以具体表示为矩阵。算子代数当然要复杂得多。但是他们也得出相当丰富的结果。首先，任何冯·诺伊曼代数可以分解为因子的直积，下面的问题就是把因子进行分类。他们通过维数函数把因子分成五型：Ⅰ_n，Ⅰ_∞，Ⅱ₁，Ⅱ_∞，Ⅲ，而且进一步研究它们之间的同构关系。Ⅰ_n型是有限维的矩阵代数，Ⅰ_∞型是希尔伯特空间上所有有界线性算子构成的代数。但是，Ⅱ型和Ⅲ型是一些怪东西。他们发现了Ⅰ_n型因子不只一个，其后进展缓慢，只是到20世纪60年代末，算子代数才取得新的突破，对于Ⅱ型和Ⅲ型因子的分类及结构研究取得比较完整的结果。

Ⅱ₁型结构显示出维数不是整数，可以是0与1之间任意一个实数的对象。为研究这种对象，冯·诺伊曼在1935年秋天创造了“连续几何学”及其相应的代数——冯·诺伊曼正则环。当时正是格论、环论大发展的时候，这些理论引起学界很大的兴趣，并且从中引出量子逻辑的研究。

冯·诺伊曼的理论经历30年进展不大，一直到20世纪70年代初，法国数学家孔涅（Connes，Alain，1947—　）才完成冯·诺伊曼的未竟之业，对因子进行完全的分类，为此他荣获1982年的菲尔兹奖，以及2001年的克拉福德奖。到此为止，算子代数还只不过是数学领域中的一个专门分支。但近二十年来，算子代数已经成为数学和物理学的中心。冯·诺伊曼代数的推广代数一方面与拓扑学、叶状结构、动力系统、微分几何学、大范围分析、拓扑K理论、代数K理论和非交换几何有关，另一方面成为量子场论和统计物理学的基础，其前途不可限量。

3．遍历理论

遍历理论又称各态历经理论，是19世纪后半叶，统计物理学开创时期提出来的。麦克斯韦的气体分子运动论指出气体的宏观性质（压力、温度）是由位置不同、速度各异而且不断变化的许许多多分子运动的结果。我们通常用相空间来描述这个分子集体中分子的位置及速度，在总能量不变的情况下的平衡状态，分子集体可能处的微观状态很多很多，但都处于一个超曲面之上。我们用统计方法计算宏观量时，是对微观状态的各种可能性进行（加权）平均求得的。所谓遍历性假设就是随着时间的流逝所有这些状态都要经过，也就是等能量的超曲面由单一轨道组成。换句话说，不管系统在某一时刻处于什么状态，它将经过（或已经过）总能量相同的另外任何状态。

玻尔兹曼在1871年提出遍历假设之后，遭到物理学家等科学家的一致反对，后来就很少有人研究这个问题。1929年，冯·诺伊曼在对量子力学系统给出遍历假设成立的充分必要条件后，对于经典力学系统的问题也进行了思考。他到了美国后，碰到了库普曼（B.Koopman，1900—1980），库普曼告诉他，保测变换可以诱导出酉算子。而冯·诺伊曼是算子理论的创始人之一，当然对酉算子了如指掌，他对酉算子的解析性质早有研究，那么自然想到由此可以了解变换的性质，也就是得出遍历假设几乎成立的条件。1931年10月，冯·诺伊曼得到了遍历理论的第一个重要定理——平均遍历定理。他马上把自己的结果告诉了库普曼及其老师柏克霍夫（G.D.Birkhoff，1884—1944），并同他们进行讨论，指出有可能改进“个别”遍历定理。11月，柏克霍夫证明了“个别”遍历定理，并马上写文章送美国《国家科学院院报》于1931年12月发表。冯·诺伊曼的稿子投得晚，到1932年初才发表，结果给人的印象，仿佛是冯·诺伊曼稍弱的结果比柏克霍夫较强的结果得到的还晚。柏克霍夫是美国数学界的头面人物，很有势力，维纳对他很不满意。这事当然也让冯·诺伊曼感到不愉快，不过，他没有发作，仍然同柏克霍夫父子保持相当好的关系。后来柏克霍夫和库普曼联合发表一篇文章，把数学的遍历理论的开创历史如实地进行叙述，才算了结这桩公案。

在20世纪30年代的早期工作之后，70年代以后遍历理论又取得巨大突破，它不仅推广到微分动力系统之上，而且原先的哈密尔顿动力系统的遍历性取得重大进展，成为蓬勃发展的热门学科。这些，与冯·诺伊曼奠基性的工作是不可分的。数学大奖沃尔大奖的获得者柯尔莫戈洛夫和辛耐（Sinai，Yakor，1935—　）对遍历理论都作出了突出贡献。同时遍历理论在信息论和编码理论上也有重要作用，而且与组合学和数论等分支有着不可思议的联系。

4．其他

冯·诺伊曼在纯粹数学方面还有许多贡献，下面列举其中两个：

①对于紧群解决希尔伯特第五问题。也就是如果紧致拓扑群，局部同胚于欧氏空间，就是李群。早在1927年，冯·诺伊曼已证明一般线性群的闭子群是李群，后来嘉当（E.Cartan，1869—1951）指出其证明方法也可用于任何李群的闭子群上。另外，冯·诺伊曼对于一般拓扑群的结构有深刻的认识，知道它像实数一样具有代数结构及拓扑结构，因此，可以像实数一样在其上引进测度、积分与概周期函数，发展一套分析理论，这对数学以后的发展是至关重要的。另外他也独立得出哈尔测度的概念并证明其唯一性。

②测度论。冯·诺伊曼用自己的群论知识来解释豪斯道夫—巴拿赫—塔斯基悖论。这个悖论最简单的情形就是两个不同半径的三维实心球体（因此体积不等）都可以分解成有限多个子集，使得这些子集可以两两重合（因此体积相等）。四维及四维以上实心球也有同样悖论，但一维实心球（闭线段）和二维实心球（闭圆盘）就没有这样的分法。冯·诺伊曼的解释是三个或三个以上变元的正交群都包含非交换的自由群，而一复元及二复元正交群则不包含这种群。

二、应用数学

1．量子力学的数学基础

冯·诺依曼对数学物理的首要贡献是用泛函分析为量子力学奠定数学基础。其系统表述发表在1932年出版的《量子力学的数学基础》一书中。

1900年以前的物理学以牛顿力学和麦克斯韦的电磁理论为核心，能够解释当时所知的几乎所有的宏观现象，被称为经典物理学。19世纪末到20世纪初，出现一些用经典物理学难以解释的现象和问题，其中涉及微观世界的理论被称为量子力学。

量子物理的缔造者有普朗克（Max Planck，1859—1947）、爱因斯坦（Albert Einstein，1879—1955）、玻尔（Niels Bohr，1885—1962）、玻恩（Max Born，1882—1970）、德布罗意（Louis de Broglie，1892—1987）、海森伯（Werner Heisenberg，1901—1976）、薛定谔（Erwin Schrodinger，1887—1961）、狄拉克（Paul Dirac，1902—1984）、费米（Enrico Fermi，1901—1954）等。量子理论是从1900年到1925年发展起来的。它的三个里程碑是1900年普朗克首先用量子假设解释黑体辐射现象。1905年，爱因斯坦用光量子理论解释光电效应，而这用经典电磁理论是完全无法解释的，这是最为关键的。1913年，玻尔用量子假设成功地解释氢光谱，从而确定量子理论是不可动摇的地位。然而，很长时期，人们很难理解光究竟是波动还是粒子，或者说什么时候是波动，什么时候是粒子。

最为重要的突破是1924年法国物理学家德布罗意提出更为大胆的推广，不仅光，而且所有物质粒子，都有波—粒二象性，而且表征波动的物理量、动量与能量之间有着简单的对应关系

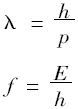
其中h为普朗克常数。物理学与数学不同，公式虽然漂亮，但需要实验证明，最典型的实验就是当时确认的电子如何表现出只有波动才有的干涉及衍射现象。

1925年和1926年标志着量子力学的诞生。海森伯引进矩阵力学来计算原子光谱，而薛定谔引进波动力学和薛定谔方程，两人互不相让。1926年大数学家希尔伯特对此感兴趣，自然引起他的助手冯·诺依曼的注意，他引入希尔伯特空间及其算子的谱理论，一举证明这两种形式等价，并给出量子力学严格的数学基础。

当时的物理学家对于数学并不特别在意，海森伯的矩阵力学随意地把有限维矩阵推广到无穷维，狄拉克引入难于处理的δ函数。

冯·诺依曼给出严格的数学概念，并把物理学的基本假定作为公理来表述。

①物理系统的状态是希尔伯特空间的点。

②可观测物理量是在希尔伯特空间中稠密定义的埃尔来特算子（物理学中称厄米算符），它通常是无界的。

牛顿力学及麦克斯韦的电磁学乃至爱因斯坦的狭义相对论的数学基础，都是物理学家自己奠定的。量子力学却不一样，物理学家不是不了解当时已发展的新数学，就是搞一些不怎么严格的数学（如狄拉克的函数）。海森伯用的是格丁根大学学过的矩阵论，可是当时数学家常用的矩阵，对于物理学家还很陌生。从那以后，线性代数才开始成为必修课。而薛定谔在1926年得出以他的姓命名的著名方程，自己却不会去解，可是在1924年出版的希尔伯特和库朗的名著《数学物理方法》中早已有其解法了。数学及物理学这种史无前例的脱节只能靠冯·诺伊曼这样的全才来补全。《量子力学的数学基础》在1932年出版德文版之后，已经译成世界各种主要文字（只有中文是明显的例外）出版，它重新恢复过去数学及物理学那种相得益彰的关系：量子力学有了可靠的表述，像海森伯的矩阵力学及薛定谔的波动力学等价性在希尔伯特空间的框架内有了完满的数学证明。同时，冯·诺伊曼为此还发展了希尔伯特空间及其上的线性算子理论，这已成为现代泛函分析的基础。凡是要对量子力学基础提出挑战的话，比如现在争论得还很热闹的“测量问题”，特别是玻姆（David Bohm，1917—1992）等人提出的隐参数问题，都要回到冯·诺伊曼的前提。其后，冯·诺伊曼与其他人合作研究过的“量子逻辑”、“量子代数”等至今仍是许多学者研究的主题，它们也是涉及当前的最大热门之一量子计算、量子通信、量子计算机及算法的基础之一。量子力学基础仍然是物理学家和数学家热心研究的问题。例如，菲尔兹奖获得者费弗曼（Charles Fefferman，1949—　）就用调和分析来表述海森伯的测不准原理。

冯·诺伊曼不仅建立量子力学的数学基础，他还进而为量子统计力学奠定基础。他引进量子熵以及正则系统的密度矩阵。1929年，他还进而表述及证明量子系统的遍历定理。这些并非他在物理学上的唯一贡献，特别值得一提的还有他在群论以及天体物理的工作。

2．流体力学与天体物理学

冯·诺伊曼对理论的研究及在军事上的应用使他对流体力学特别关注。数学物理中许多可解的方程是线性的，例如电磁学的麦克斯韦方程及量子力学的薛定谔方程，这些都产生出漂亮的理论，同时也有许多实际应用。流体力学是数学物理研究中最薄弱的环节，其方程是非线性的，而且关于流体的理论也是比较弱的。然而，从航空到炮弹乃至原子弹爆炸都离不开流体力学，这就不能不推动冯·诺伊曼从多条途径考虑问题，当然首先是理论，同时他对于由此产生的计算尤为关注。由于计算机的问世，他为激波、爆炸波的计算设计了算法。

在天体物理学方面，冯·诺伊曼早在1935年就对相对论中的爱因斯坦场方程进行过研究，更重要的是他同天体物理学家钱德里塞卡（S.Chandrasekhar，1910—1995）合作发表题目都为《由随机的量体分布引发的引力场的统计》的两篇论文。钱德里塞卡是出生于印度的天体物理学家，在1983年获得诺贝尔物理学奖。

三、博弈论及数理经济学

冯·诺伊曼是在传统的数学物理学和数理统计学之外创立第三大类应用数学的主要人物。这第三大类应用数学的名称往往称为运筹学、管理科学、系统分析或决策科学。在这一学科族中，博弈论是第一个有着完整表述的系统的数学分支。冯·诺伊曼这方面的论著在二次大战前只有三项，即他单独写的两篇论文和同摩根斯顿合著的《博弈论与经济行为》。这三项论著实际上为博弈论的提出奠定了基础。第一篇论文于1926年在格丁根数学会上宣读，1928年发表，主要讨论有限二人零和对策，证明最优策略存在，并推广到有限三人零和对策，引进特征函数，它后来推广成沙普利（Shapley）值。

第二篇论文是讨论一般经济均衡理论，这个理论至少可以追溯到19世纪70年代瓦尔拉（Walras，Leon，1834—1910）的工作。冯·诺伊曼的论文直接应用拓扑学建立均衡的存在理论。他首先于1932年在普林斯顿的会议上宣读这篇论文，其后于1938年用德文发表，1945年译成英文出版。

早在1928年，冯·诺伊曼已证明博弈论的基本理论。他引进的效用函数以及公理化都是以后研究的出发点。他研究的一般经济均衡的方法——不动点理论，一直沿用至今。

冯·诺伊曼和摩根斯顿所著《博弈论与经济行为》于1944年初出版，1947年再版，1953年三版。它在一定条件下，证明任何人对策解的存在性和唯一性。这600多页的论著有三分之二讨论合作对策，其中包括大量的概念和技术。

经济学中，冯·诺伊曼用博弈论的思想来分析生产模型，这样就为均衡点的存在及计算打下了基础。到20世纪60年代，各种数值方法的出现实际上都来源于他的工作。

冯·诺伊曼的工作从方法上标志着数理经济学的新时代的来临。他的方法证明，现代数学的公理思想，抽象的概念对于实际问题一样有着巨大的应用价值。他的哲学观点预示着未来数学家的工作——数学家可以在极其广泛的领域中选择课题进行研究。无论是博弈论还是其他数学理论与经济学的结合都已经取得而且必将继续取得重大进展。这已为1994年、2005年诺贝尔经济学奖授予研究博弈论的三位数学家而证实。

四、计算机科学及应用

电子计算机的历史意义是怎么强调也不过分的，但是与其他人不同，冯·诺伊曼对于电子计算机的贡献是全方位的，主要可分为以下几方面。

1．电子计算机的设计

电子计算机的革命作用以及冯·诺伊曼所起的作用已是众所周知的了。冯·诺伊曼对计算机设计作了根本的改进（特别是程序内存的思想），以致现在几乎所有计算机均为冯·诺伊曼型计算机。许多人提到的非冯·诺伊曼型计算机至今还不成熟，而且也依赖于他的自动机思想。他的另一个重要思想是区分硬件和软件，虽然软件这词一直到20世纪60年代后期才出现。

早在1946年，冯·诺伊曼和哥德斯坦研究编程序的问题，他们发明所谓“流程图”来沟通数学家要计算的问题的语言和机器的语言。他们采用一些子程序，而且采用自动编程序的方法把“程序员”的语言翻译成机器语言，这样大大简化了程序员编制程序的烦琐步骤。

从某种意义上来讲，冯·诺伊曼是现代数值分析计算数学的缔造者之一。他对计算机的各种可能性进行了广泛的研究和探索，特别是对于计算机广泛使用的线性代数的计算的研究（比如求解高阶线性方程组，求特征根、矩阵求逆等），设计了计算程序，研究了误差范围。他最感兴趣的是流体力学问题。要把连续问题化成计算机能做的离散问题就必须考虑数值稳定性，也就是离散方程的解收敛于原来解的问题，以及误差的积累和传播的问题。对于解决这个问题，他做了大量奠基性的工作。由于有了计算机，还要发展适合于计算机的算法，特别值得一提的是他协助乌拉姆等人发表了蒙特卡罗（Monte-Carlo）算法（1949年首次发表），这种方法是把数值计算问题化成为统计抽样问题，通过大量抽样而计算出结果来。

冯·诺伊曼念念不忘使用计算机“摸规律”，由于他的早逝没能完成这方面的工作。费米、乌拉姆等人在他的影响下于1954年进行著名的非线性谐振子计算机实验。这个实验经过改进，在1967年终于得到浅水波方程的孤立子解，由此显示了计算实验的伟大启发力量。

现在对冯·诺伊曼串行计算机的最大改进是并行计算机的开发与使用，可是，最早提出并行计算观念的还是冯·诺伊曼。50多年之后的今天，我们还没有跳出这位天才的思想领域。

2．计算机的应用

本来设计计算机是为了用来计算弹道的，但第一台电子计算机（ENIAC）问世时，二战早已结束。这时，冯·诺伊曼就以非凡的远见卓识，为计算机找新的用场。电子计算机第一项重大贡献是数值天气预报，这完全是冯·诺伊曼的亲自组织以及与气象学家密切合作的结果。

1946年，冯·诺伊曼刚回到普林斯顿，就把数值天气预报作为考验电子计算机的头号课题。这个选题非常合理，因为：

（1）天气预报的基本方程组是流体动力学方程组，人们一直对它的解析解无能为力，而且只有通过计算机才能对解的性质有着一些了解。

（2）天气预报无疑有极大的实用价值。

（3）1922年英国应用数学家理查孙（Lewis Fry Richardson，1881—1953）已经提出一个合理的数学模型，只是由于计算太慢，当天的天气只能在后天或大后天才能预报出来，只有快速的计算机才能完成提前预报天气的任务。

（4）数值预报必定使大规模科学计算的问题暴露出来，从而促使冯·诺伊曼建立有效的数值方法和数值分析，其中首要的问题是误差的来源和误差的传播，它可能造成计算的不稳定性，同时误差可能放大到同数据相同的数量级，使得计算结果完全没有意义。

1948年，气象学家查尼（J．C Charney，1917—1981）来到普林斯顿。他对流体动力学方程组进行适当简化，排除掉对应于高速声波和重力波的解，而其余的解保持不变。这样他不仅简化了方程，而且绕过引起不稳定的因素，从而把问题带入可计算的范围。1948年秋天，冯·诺伊曼和查尼等进一步研究地球表面的影响，1949年，设计出数值实验、数值方法都用差分法的方程，计算的稳定性满足1928年库朗等人提出的条件，初始条件取自北美上空的数据，程序由冯·诺伊曼等人设计。1950年4月用ENIAC成功地进行计算，得出精确的结果。其后把这个最简单的方程推广，加入更多的实际效应，得出简单的三维模型。1953年在普林斯顿用计算机MANIAC进行实验，已能预报风暴的发展。由于冯·诺伊曼为首的科学家的努力，1954年起天气预报成为例行公事。

3．发展数值分析（Numerical Analysis）

电子计算机使大规模数值计算成为可能，但也带来不少理论问题。首要的问题，是经大量计算后，减少（舍入）误差的积累对结果精确度的影响。计算机的算法必须误差影响小，也就是具有数值稳定性。

1946年，冯·诺伊曼和伯格曼（S.Bergman，1898—1977）及蒙哥马利（D.Montgomery，1909—1992）为美国海军部写了一个报告《高阶线性方程组求解》，但未发表。1947年，冯·诺伊曼和哥德斯坦发表题为《高阶矩阵数值求逆》，首先对线性方程组高斯（Carl Friedrich Gauss，1777—1855）消去法进行误差分析而开辟了数值分析这一领域。同年美国国家标准局建立国家应用数学实验室，并建立数值分析研究所。冯·诺伊曼这些开创性的工作以及一系列研究机构的建立都表明数值分析脱离开传统的数学分析而成为独立分支。在此之前，一系列的计算方法［如有限差分法、黎茨（Ritz，1878—1909）方法等］虽已发明，但是不一定适用于计算机。此后，特别着重于研究计算机计算方法。冯·诺伊曼的工作为科学与工程计算奠定了基础。

4．建立新算法

蒙特卡罗算法与传统的数学算法完全不同，是靠掷骰子来求近似值的。这种思想早在18世纪就有，维纳也曾有过类似想法。1945年底，乌拉姆首先想到，后来同冯·诺伊曼多次讨论而成为一个有效的、适用于计算机的算法。用他们的话来说，这是“使用随机数来处理确定性问题的方法”。1949年，蒙特卡罗算法正式发表之后，引出大量理论研究及应用。它几乎可以用于所有的问题及领域，在高维问题（例如求高维区域的体积）有着其他方法无法比拟的优点，而且对许多问题是不能用其他方法来替代的。

蒙特卡罗算法的意义不仅仅在于它是一个优秀的算法，还在于它开辟了与数值计算完全不同的道路——即非决定模型和随机算法。无论是人计算还是计算机计算，错误及误差是经常存在的，而且并不像人们所想象的那样容易被消除。现在，随机算法已经是一个不可忽视的重要领域。

5．开拓自动机理论

冯·诺伊曼晚年的兴趣在于发展一般的自动机理论，这可以看成他早期对数理逻辑的工作以及他以后对计算机研制工作的综合。其中他研究了两个最复杂的问题：一是如何用不可靠的元件来设计可靠的机器；二是如何建造自繁殖机。自动机是计算机的理论模型，也是改进计算机功能的必经途径。在人们还刚刚对新生的计算机赞叹不已时，冯·诺伊曼已远远走到他们的前头：计算机怎样才能成为名副其实的电脑。他没有来得及完成他一生最后一项大计划，但遗留下来的思想还在继续指导今后的工作，他把机器和人脑进行了细致的比较，明确指出人脑与计算机显著不同之处是它由不可靠元件组成可靠的机器，他预示了信息传输理论、编码理论、可靠性理论乃至模糊数学理论。他还提出两种方法去设计网络，使错误减到某固定值之下。此外，冯·诺伊曼还研究自繁殖机并且设计了两套模型，其中第二套模型是无穷方阵，在结点处是“细胞”——它具有29个可能的状态，每个细胞的状态由前一时刻的四个相邻细胞的状态决定。这样整个细胞阵列就可以由原来某种静寂（死）状态变成活状态，从而达到“活”细胞的繁衍增殖。他还考虑这种自繁殖机的“进化”问题，这里他考虑了复杂性问题——这也是现代计算机科学一大热门，同时对比生物体提出了这种自动机的临界大小问题。

历史评价

尽管冯·诺伊曼已经过了他的百年华诞，去世也超过了半个世纪，我们仍然在享用他的科学遗产。

20世纪已经过去快十年了，其间，有成百上千项科学技术成就影响着时代的发展、社会的进步，冲击我们的生活、工作和思想。爱因斯坦因其广义相对论（一个推论是质能关系）、一般相对论、量子理论、激光理论等开创性的贡献，被公认为20世纪最伟大的科学家。他似乎是原子时代的象征。长期以来，原子弹是悬在人类头上的达摩克拉斯之剑。随着冷战结束，突然间，世界由原子时代进入比特时代，更通俗地说进入信息时代，而信息时代的中心无疑是电脑。如果说，冯·诺伊曼是电子计算机之父，肯定有许多人不赞成，发明电脑的优先权甚至也引起法律纠纷。可是，谁有资格做比特时代的象征呢？恐怕非冯·诺伊曼莫属。

计算机发展到今天，无疑是物理学（电子学）与数学相结合的产物。然而，计算机的研发及使用主要靠数学。数学是计算机得以广泛应用的幕后英雄。而这正是冯·诺伊曼的中心思想。冯·诺伊曼不仅主导计算机的设计，而且其设计思想在各个领域有着更广泛的应用。他开拓了当前蓬勃发展的四大领域：①计算机科学；②数值分析；③算法设计；④计算机实验（现在发展为实验数学）。

这些都是与数学密切相关的领域，也是新时代的重要研究方向。单单这些已足以使他名垂青史。但是，冯·诺伊曼看得更远，他很早就认识到计算机改变世界的巨大潜能，而当时很少有专家能够意识到这一点。其中最典型的就是数值天气预报。可以说，这项影响我们日常生活的事业，要是没有冯·诺伊曼的首创实现起来会困难得多。冯·诺伊曼的远见卓识还不止于此，他还有一个梦想，那就是控制天气。这是他没能预见到其难度的少数猜想之一。因为当时大家对于所谓“浑沌”还一无所知，另外，大气团的能量控制作用方式也很复杂。冯·诺伊曼去世50年后，我们仅能局部地，一时地“呼风唤雨”，对于灾害性天气的预报尚有困难，更不用说冯·诺伊曼想象的控制与利用了。

我们现在已实实在在地进入信息时代，实际上，1945年之后由于原子弹的爆炸，几乎所有人都只关心“核”问题，只有冯·诺伊曼认识到未来属于大型、快速、高存储的计算机，正是他的远见卓识成就了这个新时代。

冯·诺伊曼开创的另一大领域可以统称为“决策科学”，他也应该被尊称为决策科学之父。这门科学在第二次世界大战前后可以说方兴未艾，正是冯·诺伊曼等人把它变成一个必不可少的领域。其核心部分是他开创的博弈论。另一部分是运筹学以及其中最活跃的一部分——数学规划理论，正是他有效地运用线性规划方法，超越了代数方法及分析方面（微积分），从而使线性规划方法成为最有效的应用数学工具之一。

人类有史以来就不可避免地要进行决策，但多数情况下是少数人拍脑瓜，既谈不上民主，更谈不上科学。当前社会多种因素相互作用，情况多变，许多决策者的独立决策都要求科学决策。科学决策要包括合理的逻辑及数学表述，对数学问题的术解，以及对各种可能后果的预测。正由于冯·依诺曼的工作，博弈论已从纯数学变为经济学的重要组成部分。

冯·诺伊曼在纯粹数学与应用数学和数学物理上的巨大贡献在相关领域也是绝对一流的。不过，计算机和决策科学这两大领域更容易为专家以外的公众所了解。

值得注意的是，作为一位如此大量的原创性贡献的大科学家，冯·诺伊曼并非只是关在书斋中的学者，而是在实际事务中也起着非凡作用的非凡人物。

一位科学家有如此大的影响已是惊人的了。冯·诺伊曼还有其他的方面使他无可超越，主要表现在他的战略性思考。他所处的时代是十分动荡的时代：20世纪30年代是法西斯上台、第二次世界大战即将爆发的时期，而1945年之后则是冷战时期。在战前，他深刻认识到战争必将爆发，不能抱有任何和平幻想，同时，他预测到了美国的作用，这显示了他非凡的洞察力。他在1939年就说过，“我承认，美国将会成为帝国主义者。如果在20年内它成为帝国主义者我不会感到奇怪。然而，它现在还不是。”现在人可能根本不了解，1939年美国因孤立主义盛行而想置身战争之外，甚至都反对战时援助英国，而冯·诺伊曼早就预见到美国必然参战这种趋势。这些都是在21世纪发表的冯·诺伊曼的信中见到的。冯·诺伊曼在二次大战之中和其后就更有洞察力了。在许多方面他是持少数意见者。一句话，他是鹰派中的鸽派。冷战时期先是和平幻想甚嚣尘上，当苏联如冯·诺伊曼所预料那样很快制造出核武器时，美国的麦卡锡主义开始盛行。从1950年到1954年，麦卡锡主义对美国有着极大杀伤力。冯·诺伊曼则坚持，在培养科学人才时除了能力之外不要有其他的考虑。冯·诺伊曼没能看到苏联卫星上天，只有到这时，美国人才意识到自己教育与人才的弱势地位而奋起直追。

主要参考文献

［1］John von Neumann. Collect Works of John von Neumann. A.H.Taub, ed.（共6卷）N.Y.Pergamon Press, 1961.

［2］John von Neumann. Mathematische Grundlagen der Quantenmechanik. Springer, 1932.

［3］John von Neumann. O.Morgenstern. Theory of games and economic behavior, Princeton: Princeton Uni. Press, 1944，第二版，1947，第三版，1953.

［4］John von Neumann. The Computer and the Brain. Yale: Yale University Press, 1958.

［5］John von Neumann. Selected letters. Miklòs Rédei, ed. Providence, RI, American Mathematical Society, 2005.

［6］John von Neumann. Papers of John von Neumann on computing and computer Science. Aspray and Arthur W.Burks, eds. Cambridge, Mass.: MTT Press, 1987.

［7］N.Macrae. John von Neumann. New York: Pantheon Books, 1992.

［8］S.J.Heims. John von Neumann and Norbert Wiener. Cambridge, Mass.: MIT Press, 1980.

［9］S.M.Ulam. etc. John von Neumann（1903—1957）. Bull Amer, ed. Math. Soc vol.64.Supp, 1958.

［10］S.M.Ulam. Adventures of a Mathematician. New York: Charles Scribner's Sons, 1976.

［11］H.Goldstine. Thw computer from Paseal to von Neumann. Princeton: Princeton University Press, 1972.

［12］M.Dore et.al（eds.）. John von Neumann and Modern Economics. Oxford University Press, 1989.

［13］I want to be a Mathematician, Paul R.halmos. New York: Springer-Verlag New York, Inc, 1985.

［14］Burks, Arthur W. Theory of Self-Reproducing Automata. Urbana: University of Illinois Press, 1966.

［15］Aspray, William. John von Neumann and the Origins of Modern Computing. Cambridge Mass: MTT Press, 1990.

［16］胡作玄．冯·诺伊曼：二十世纪的天才数学家，自然辩证法通讯（2），1984，67—68。

［17］Glimm, et.al（eds）. The Legaey of John von Neumann. RI Providence, American Mathematical Society, 1990.