2.5.13　使用并行计算求圆周率π

关于圆周率大家再熟悉不过了，我们从课本上学习到早在一千多年前，祖冲之将圆周率计算到3.1415926到3.1415927之间……计算机诞生后，计算圆周率被用来检测计算机的硬件性能，昼夜燃烧CPU看会不会出问题……另外一些人也想看看这个无限延伸的神秘数字背后是否有规律，是否能发现一些宇宙的秘密……

提起圆周率，不能不提及Fabrice Bellard，他被认为是一位计算机天才，在业界有着重要的影响。1996年他编写了一个简洁但是完整的C编译器和一个Java虚拟机Harissa。Fabrice Bellard发明的TinyCC是GNU/Linux环境下最小的ANSI C语言编译器，是目前号称编译速度最快的C编译器。Fabrice Bellard杰作众多且涉及广泛，1998年编写了一个简洁的OpenGL实现TinyGL，2003年开发了Emacs克隆QEmacs，2005年还设计了一个廉价的数字电视系统。如图2-33所示。

图2-32　多机迭代

Fabrice Bellard使用一台普通的台式电脑，完成了冲击由超级计算机保持的圆周率运算记录的壮举，他使用台式机将圆周率计算到了小数点后2.7万亿位，超过了由目前排名世界第47位的T2K Open超级计算机于去年8月份创造的小数点后2.5万亿位的记录。

Bellard使用的电脑是一台基于2.93GHz Core i7处理器的电脑，这部电脑的内存容量是6GB，硬盘则使用的是五块RAID-0配置的1.5TB容量的希捷7200.11，系统运行64位Red Hat Fedora 10操作系统，文件系统则使用Linux的ext4.

这次计算出来的圆周率数据占去了1137GB的硬盘容量，Bellard花了103天的时间计算出了这样的结果。

计算圆周率的方法有很多种，下面介绍几种。

（1）微积分割圆法

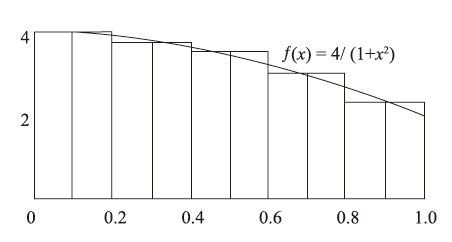
（2）利用便于计算机计算的丘德诺夫斯基公式法

不过这些计算方法都比较复杂，难以让读者理解和使用并行计算来求。所幸数学上的泰勒级数是个好东西，它将微积分的东西改成用无限级数来表示，这样很容易进行并行计算分解：

π=4*∑（-1）^n+1/（2n-1）

或者写为：

π=4*（1-1/3+1/5-1/7+…）

也可以得到：

πn=πn-1+（-1）^n+1/（2n-1），也就是可以通过迭代前面的π值去求当前π值。

我们根据上面公式先写个单机程序，如下所示：

public class PiTest
{
        public static void main(String[] args)
        {
           double pi=0.0;
           for(double i=1.0;i<1000000001d;i++){
                pi += Math.pow(-1,i+1）/(2*i-1）;
           }
           System.out.println(4*pi);
        }
}

运行以上程序，并对照pi的标准值：3.141592653589793238462643383279…

❏　如果i<10000，得到pi=3.1416926635905345（从阴影部分以后不精确了）

❏　如果i<1000000，得到pi=3.1415936535907742（同上）

❏　如果i<1000000000，得到pi=3.1415926525880504（同上）

可以看到，当迭代的轮数越大，求出的π值越精确。

由于是无限累加，我们可以很容易改成并行程序求解，比如i=4n，可以分成4段并行求解，再将4部分和合并起来得到最终π值。假设我们有4台计算机，并行计算设计如图2-34所示。

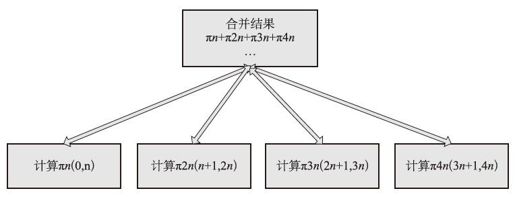
图2-34　并行计算方式求圆周率

程序实现的方法如下：

❏　PiWorker：是一个π计算工人实现，我们可以看到它通过命令行输入一个计算π值的起始值和结束值，我们同时启动4个PiWorker实例，启动时指定不同的起始结束参数。

❏　PiCtor：是一个π计算包工头实现，它的实现很简单，获取到线上工人后，通过doTaskBatch进行阶段计算，等待每个工人计算完成后，将各工人返回的π计算结果合并累加。

运行步骤：

1）启动ParkServerDemo，它的IP端口已经在配置文件指定，如图2-35所示。

java -cp fourinone.jar; ParkServerDemo

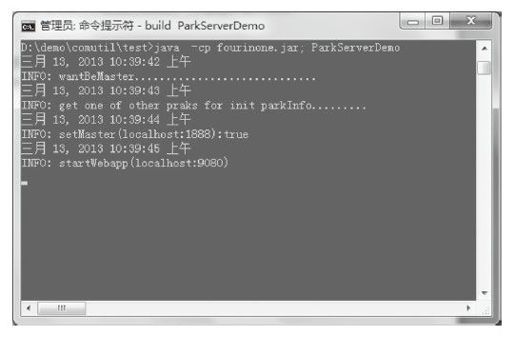
图2-35　ParkServerDemo

2）运行4个PiWorker，将迭代100000000轮的计算拆分到4个工人并行完成，这里方便演示是在同一台机器上，现实应用中可以在多台计算机上完成，代码如下，如图2-36所示。

java  -cp fourinone.jar; PiWorker localhost 2008 1 250000000
java  -cp fourinone.jar; PiWorker localhost 2009 250000000 500000000
java  -cp fourinone.jar; PiWorker localhost 2010 500000000 750000000
java  -cp fourinone.jar; PiWorker localhost 2011 750000000 100000000

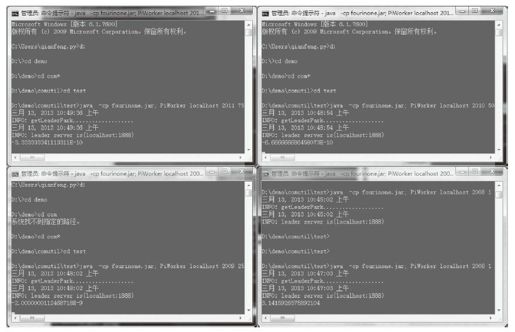
图2-36　PiWorker

3）运行PiCtor，代码如下，如图2-37所示。

java  -cp fourinone.jar; PiCtor

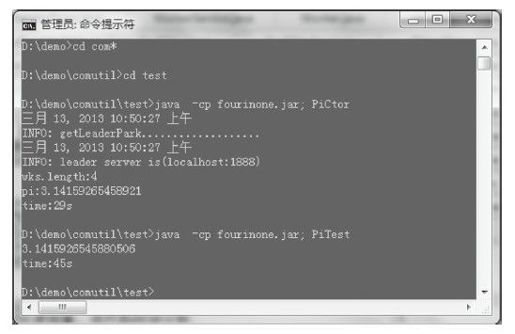
图2-37　PiCtor

提示

4个工人实例在同台机器并行完成计算π值的时间为29秒，如果是运行单机程序PiTest完成的时间在45秒，精准度都是到小数点后8位“3.14159265”，但是耗时上有明显差距，如果多机多实例，效率还会进一步提升，并行计算性能提升分析可以参考2.5.12节“使用并行计算大幅提升递归算法效率”。

完整demo源码如下：

// ParkServerDemo
import com.fourinone.BeanContext;
public class ParkServerDemo
{
        public static void main(String[] args)
        {
           BeanContext.startPark();
        }
}
 
// PiWorker
import com.fourinone.MigrantWorker;
import com.fourinone.WareHouse;
 
public class PiWorker extends MigrantWorker
{
        public double m=0.0,n=0.0;
 
        public PiWorker(double m, double n){
           this.m = m;
           this.n = n;
        }
 
        public WareHouse doTask(WareHouse inhouse)
        {
           double pi=0.0;
           for(double i=m;i<n;i++){
               pi += Math.pow(-1,i+1）/(2*i-1）;
           }
 
           System.out.println(4*pi);
           inhouse.setObj("pi",4*pi);
 
           return inhouse;
        }
 
        public static void main(String[] args)
        {
           PiWorker mw = new PiWorker(Double.parseDouble(args[2]),Double.                             parseDouble(args[3]));
           mw.waitWorking(args[0],Integer.parseInt(args[1]),"PiWorker");
        }
}
 
// PiCtor
import com.fourinone.Contractor;
import com.fourinone.WareHouse;
import com.fourinone.WorkerLocal;
import java.util.Date;
 
public class PiCtor extends Contractor
{
        public WareHouse giveTask(WareHouse inhouse)
        {
           WorkerLocal[] wks = getWaitingWorkers("PiWorker");
           System.out.println("wks.length:"+wks.length);
 
           WareHouse[] hmarr = doTaskBatch(wks, inhouse);
 
           double pi=0.0;
           for(WareHouse result:hmarr){
               pi = pi + (Double)result.getObj("pi");
           }
 
           System.out.println("pi:"+pi);
           return inhouse;
        }
 
        public static void main(String[] args)
        {
           PiCtor a = new PiCtor();
           long begin = (new Date()).getTime();
           a.giveTask(new WareHouse());
           long end = (new Date()).getTime();
           System.out.println("time:"+(end-begin)/1000+"s");
           a.exit();
        }
}