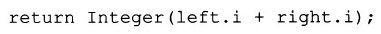12.3.3　参数和返回值

在OverloadingUnaryOperators.cpp、Integer.h和Byte.h例子中可以见到各种不同的参数传递和返回方法，乍一看让人有些摸不着头脑。虽然可以用任何需要的方式传递和返回参数，但在这些例子中所用的方式却不是随便选的。它们遵守一种合乎逻辑的模式，我们在大部分情况下都应选择这种模式：

1）对于任何函数参数，如果仅需要从参数中读而不改变它，默认地应当作为const引用来传递它。普通算术运算符（像“+”和“-”等）和布尔运算符不会改变参数，所以以const引用传递是主要的使用方式。当函数是一个类成员的时候，就转换为const成员函数。只有会改变左侧参数的运算符赋值（operator-assignment）（如+=）和operator=，左侧参数不是常量，但因为参数将被改变，所以参数仍然按地址传递。

2）返回值的类型取决于运算符的具体含义（我们可以对参数和返回值做任何想做的事）。如果使用该运算符的结果是产生一个新值，就需要产生一个作为返回值的新对象。例如，Integer：operator+必须生成一个操作数之和的Integer对象。这个对象作为一个常量通过传值方式返回，所以作为一个左值结果不会被改变。

3）所有赋值运算符均改变左值。为了使赋值结果能用于链式表达式（如a=b=c），应该能够返回一个刚刚改变了的左值的引用。但这个引用应该是常量还是非常量呢？虽然我们是从左向右读表达式a=b=c，但编译器是从右向左分析这个表达式，所以并非一定要返回一个非常量值来支持链式赋值。然而人们有时希望能够对刚刚赋值的对象进行运算，例如（a=b）.func（），这是b赋值给a后调用func（）。因此所有赋值运算符的返回值对于左值应该是非常量引用。

4）对于逻辑运算符，人们希望至少得到一个int返回值，最好是bool返回值（在大多数编译器支持C++内置bool类型之前开发的库函数使用int或者用typedef产生的等价类型）。

因为有前缀和后缀版本，所以自增和自减运算符出现了两难局面。由于两个版本都改变了对象，所以这个对象不能作为常量类型。在对象被改变后，前缀版本返回其值，我们希望返回改变后的对象。这样，用前缀版本只需作为一个引用返回*this。因为后缀版本返回改变之前的值，所以必须创建一个代表这个值的独立对象并返回它。因此，如果想保持本意，对于后缀必须通过传值方式返回。（注意，我们经常会发现自增和自减运算返回一个int值或bool值，表示诸如是否在列表上移动的对象到达了列表尾部这样的情况）。现在的问题是：它们应该按常量还是按非常量返回？如果允许对象被改变，而有的人写了表达式（++a）.func（），那么func（）作用在a上。但对于表达式（a++）.func（），func（）作用在通过后缀operator++返回的临时对象上。临时对象自动定为常量，所以这一操作会被编译器阻止。但为了一致性，两者都是常量更有意义，这里就是如此。我们可以选择让前缀版本是非常量的，而后缀版本是常量的。因为想给自增和自减运算符赋予各种含义，所以它们需要就事论事考虑。

12.3.3.1　作为常量通过传值方式返回

作为常量通过传值方式返回，开始看起来有些微妙，所以值得多加解释。现在考虑二元运算符+。假设在表达式f（a+b）中使用它，a+b的结果变为一个临时对象，这个对象用于对f（）的调用中。因为它是临时的，自动被定为常量，所以无论是否使返回值为常量都没有影响。

然而，也可能发送一个消息给a+b的返回值而不是仅传递给一个函数。例如，可以写表达式（a+b）.g（），其中g（）是Integer的成员函数。这里，通过设返回值为常量，规定了对于返回值只有常量成员函数才可以被调用。用常量是恰当的，这是因为这样可以使我们不用在对象中存储可能有价值的信息，而该信息很可能是会被丢失的。

12.3.3.2　返回值优化

通过传值方式返回要创建新对象时，应注意使用的形式。例如在operator+：

乍看起来这像是一个“对一个构造函数的调用”，其实并非如此。这是临时对象语法，它是在说：“创建一个临时Integer对象并返回它”。据此我们可能认为如果创建一个有名字的局部对象并返回它结果将会是一样的。其实不然。如果如下编写，

将发生三件事。首先，创建tmp对象，其中包括构造函数的调用。然后，拷贝构造函数把tmp拷贝到外部返回值的存储单元里。最后，当tmp在作用域的结尾时调用析构函数。

相反，“返回临时对象”的方式是完全不同的。当编译器看到我们这样做时，它明白对创建的对象没有其他需求，只是返回它，所以编译器直接地把这个对象创建在外部返回值的内存单元。因为不是真正创建一个局部对象，所以仅需要一个普通构造函数调用（不需要拷贝构造函数），且不会调用析构函数。这种方法不需要什么花费，因此效率是非常高的，但程序员要理解这些。这种方式常被称作返回值优化（return value optimization）。