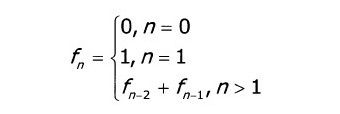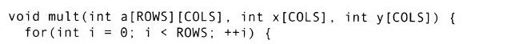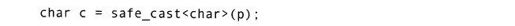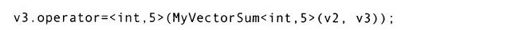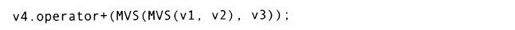5.6　模板元编程

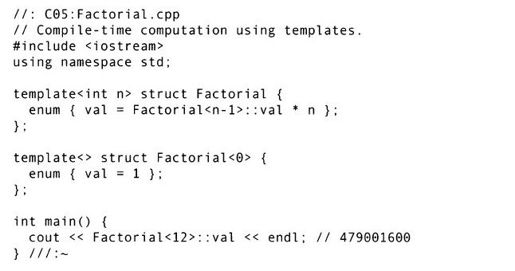
1993年，编译器开始支持简单的模板构造，因此用户可以定义通用的容器和函数。同一时期，C++标准委员会也正在考虑将STL纳入标准C++，当时在C++标准委员会的成员们周围，到处都是那些已经通过验证的精巧的和令人惊讶的程序例子^[1]，其中一个简单的例子如下所示：

程序输出了由参数12！实例化后的正确值！并没有警告发出。那么警告是什么呢？警告就是：在程序开始运行前就已经完成了计算！

当编译器试图对Factorial＜12＞进行实例化时，编译器发现必须先实例化Factorial＜11＞，而后者又要求实例化Factorial＜10＞，以此类推。这个递归最终在特化Factorial＜1＞时结束，此时计算展开，Factorial＜12＞：val由整数常量479 001 600代替，至此编译结束。由于所有的计算都由编译器来做，其包含的值必须是编译时常量，因此使用了enum。程序运行时，惟一要做的工作就是跟随一个换行符来打印这个常量的值。为了说服自己，使读者相信是Factorial的一个特化导致了产生正确的编译时结果值，可以用它作为一个数组的维数来验证一下，如下所示：

5.6.1　编译时编程

正如将进行类型参数代替作为一种方便的方法，这意味着产生了一种支持编译时编程的机制。这样的程序称为模板元程序（template metaprogram）（因为正在“为一个程序进行编程”），事实证明可以用它做很多的事情。实际上，模板元编程就是完全的图灵机（Turing complete），因为它支持选择（if-else）和循环（通过递归）。从理论上讲，可以用它执行任何的计算^[2]。上面的factorial程序例子显示了如何实现循环：编写一个递归模板，并且通过一个特化来提供一个终止递归的规则。下面的例子显示了如何利用相同的技术在编译时计算斐波那契（Fibonacci）数：

斐波那契数的数学定义如下：

前两种情况导致了上面的模板特化，第3行的规则就是基本的模板。1.编译时循环

在一个模板元程序中要计算任意的循环，首先必须再用公式表示递归。例如，若想计算整数n的p次方，下面几行程序使用了一个循环就可以完成：

也可以将它写成一个递归过程：

现在它就可以很容易地用一个模板元程序来实现：

由于N仍是一个自由模板参数，因此需要用一个半特化来作为终止条件。注意，这个程序仅当指数为非负时才运行。

由Czarnecki和Eisenecker^[3]改编的下述元程序是很有趣的，因为它使用一个模板作为模板参数，模拟传递一个函数作为另一个函数的参数。其中的“循环是通过”0..n这些数字来实现的：

基本的Accumulate模板试图计算F（n）+F（n-1）……F（0）的和。终止递归是通过一个“返回”F（0）的半特化来实现的。参数F本身就是一个模板，在本节以前的例子中它通常是一个函数。模板Identity、Square和Cube，用它们的模板参数计算自己名字表明的相应函数。在main（）函数中，Accumulate的第1个实例化计算是求和：4+3+2+1+0，因此Identity函数仅仅“返回”它的模板参数。main（）中第2行是计算这些数字的平方和：（16+9+4+1+0）。最后计算立方和：（64+27+8+1+0）。

2.循环分解

算法设计者们总是尽力优化他们的程序。其中一个是在时间方面的优化—特别是在数字计算编程中—采用的是循环分解（loop unrolling），这是一项将顶层循环的次数减到最小的技术。典型的循环分解的例子是矩阵相乘。下面的函数将一个矩阵与一个向量相乘（假设常量ROWS和COLS已经定义过了）：

如果COLS是偶数，则进行增1和比较循环控制变量j的那一层循环体，就能用将该计算“分解”的方法切成两部分，使其变成在内部循环中成对出现的两部分计算：

通常，若COLS是k的一个因子，每次内部循环迭代都可以执行k操作，大量减少顶层的循环。这种节省只有在大数组上操作才是明显的，但这正好是一个产业的强度数学计算的严谨的例子。

内联函数也构成了循环分解的一种格式。请看下面计算整数幂的方法：

从概念上来讲，编译器必须生成模板参数分别为3、2、1的3个power＜＞特化。因为每个函数的代码可以内联，实际插入main（）函数的代码就是一个单一的表达式mmm。这样一来，一个存在内联的简单模板特化就提供了一种方法，该方法可以完全避免循环控制顶层的出现^[4]。这种循环分解的方法受使用的编译器的内联深度的限制。

3.编译时选择

为了模拟在编译时的条件，可以在一个enum声明中使用3目条件运算符。下面的程序就使用了这个技术，在编译时计算两个整数之中的最大值：

如果想使用编译时条件来控制自定义代码的生成，可以利用true和false值的特化：

这个程序相当于下面的表达式：

除了条件cond在编译时确定之外，execute＜＞（）和Select＜＞的适当版本都由编译器进行实例化。函数Select＜＞：f（）在运行时执行。可以用类似的方式仿效一个switch语句，但不是用值true和false，而是特化每个case值。

4.编译时断言

在第2章中讨论了将断言（assertion）作为整个防御性编程策略的一部分的优点。断言基本上就是一个其后有一个适当动作的布尔表达式的判断：若条件为真则什么都不做，否则就停止并附带一个诊断消息。最好能尽快发现断言失败。若可以在编译时对一个表达式求值，就使用编译时断言。下面的例子使用了这个技术，它将一个布尔表达式映射到一个数组声明中：

do循环为一个数组a的定义产生了一个临时空间，这个数组的大小由一个不确定的条件所决定。定义一个大小为-1的数组是不合法的，因此当条件为假时这条语句将失败。

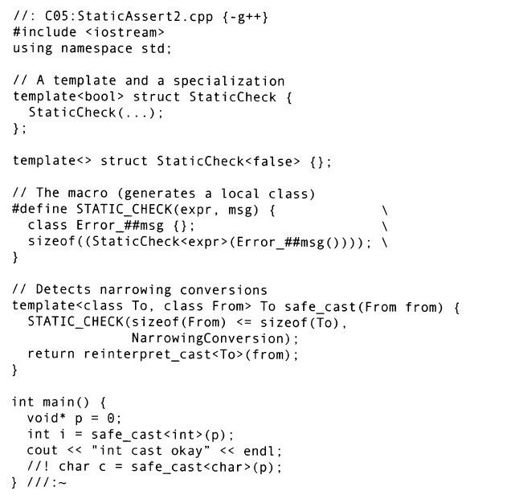
前面的内容说明了如何对编译时布尔表达式求值。在效仿编译时断言方面剩下的问题就是打印一个有意义的错误消息并且停止编译。所有的编译错误都要求编译器停止编译；解决这个问题的一个技巧是在错误消息中插入有用的文本。从Alexandrescu^[5]处获得的下面的例子使用了模板特化，一个局部类和一个小巧且奇妙的宏来完成这项工作：

这个例子定义了一个函数模板safe_cast＜＞（）用来进行两个对象长度的检查。它检查源对象类型长度是否不大于目标对象类型的长度。如果目标对象类型的长度较小，则用户将会在编译时得到通知：现正试图进行一个窄类型转换。注意，StaticCheck类模板有一个奇特的特性：任何模板参数的特化都可以被转换成StaticCheck＜true＞的实例（由于它的构造函数中的省略号^[6]），并且没有任何模板参数的特化可以被转换成StaticCheck＜false＞的实例，因为没有为这种特化提供转换。它的思想是：在编译时如果相关条件在测试时为真，就创建一个新类的实例并且将它转换成为StaticCheck＜true＞对象；或者当条件在测试时为假，将它转换成一个StaticCheck＜false＞对象。由于sizeof运算符在编译时完成它的工作，因而用它来执行转换任务。当条件为假时，编译器将做出解释：它不知道如何将这个新类类型转换成StaticCheck＜false＞对象。（在STATIC_CHECK（）中的sizeof调用里面的特殊圆括号，是为了防止编译器认为程序正在试图将sizeof作为函数调用，这是不合法的）。为了在错误消息中插入一些有意义的信息，新的类名在它的名字中携带了关键且有意义的文字信息。

理解这项技术的最好的方式就是使其融入程序，请看上面例子main（）中的这一行：

safe cast＜int＞（p）的调用包含了下面的宏扩充代码，它代替了第1行代码：

（回忆一下标记传递预处理操作符：##，它将它的操作数连接为一个单一标记，因此经过预处理后Error##NarrowingConversion变成了标记Error_NarrowingConversion。）Error_NarrowingConversion类是一个局部类（意味着它在一个非名字空间作用域内声明），因为它无需在这个程序的其他地方使用。这里sizeof运算符的使用试图决定StaticCheck＜true＞的实例的大小（因为在本程序使用的系统平台上sizeof（void*）＜=sizeof（int）为真），由Error_NarrowingConversion（）调用返回的临时对象隐式产生。编译器知道新类Error_NarrowingConversion的大小（它为空），因此在编译时sizeof在STATIC_CHECK（）中外层的使用是合法的。由于从Error_NarrowingConversion临时对象转换到StaticCheck＜true＞实例取得成功，因而这个sizeof的外层应用和执行都可以继续。

现在来看看，如果main（）函数中最后一行的注解被去掉将会发生什么事情：

在这里，把safe_cast＜char＞（p）中的STATIC CHECK（）宏扩充为：

由于表达式sizeof（void*）＜=sizeof（char）为假，此时程序将尝试进行从Error_NarrowingConversion临时对象到StaticCheck＜false＞实例的转换，如下所示：

它失败了，所以编译器将发出一个如下的消息并停止工作：

类名Error_NarrowingConversion是由编码人员巧妙设计的有意义的消息。通常为了用这种技术来执行一个静态断言，应该调用STATIC_CHECK宏去进行编译时条件检查，并且用一个有意义的名称（函数名称、参数名称、模板名称等）来描述这个错误。

5.6.2　表达式模板

模板最强大的应用大概是在1994年由Todd Veldhuizen^[7]和Daveed Vandevoorde^[8]分别提出的一类模板技术：表达式模板（expression template）。表达式模板能够使某些计算得到的全方位的编译时优化，这些优化产生这样一些代码，其执行起来至少像支持优化的Fortran（专门用于科学计算的编程语言）代码一样快速，并且通过运算符重载仍旧保持了数学的原始符号。尽管可能在日常编程中并不使用这种技术，但它是由C++编写的许多复杂的高性能数学库的基础。^[9]

为了引发读者学习表达式模板的兴趣，请看一个典型的数值线性代数的运算，将两个矩阵或向量相加^[10]，如下所示：

按照一般初学者的实现方式，这个表达式将会导致一些临时变量的产生—一个是A+B，一个是（A+B）+C。当这些变量代表极大的矩阵或向量时，这种方法将会耗尽系统的资源的确让人无法接受。表达式模板允许在没有临时变量的情况下使用同一个表达式。

下面的程序定义了一个MyVector类来模拟任意大小的数学向量。在程序中使用一个无类型的模板参数来表示向量的长度。程序还定义了一个MyVectorSum类来担当一个中间代理类，用其计算MyVector对象之和。这将允许使用惰性计算，因而向量的各个组成部分的相加不需要临时变量就可以执行。

当MyVectorSum类产生时，它并不进行计算；它只是持有两个待加向量的引用。仅当访问一个向量和的成员（即它的operator[]（））时计算才会发生。为了对MyVector的赋值操作符进行重载，将MyVectorSum作为一个表达式的参数来使用，如下所示：

当对表达式v1+v2求值时，返回一个MyVectorSum对象（实际上，是一个插入的内联对象，因为operator+（）已经声明为inline）。这是一个很小的、固定大小的对象（它仅仅持有两个引用）。然后调用上面提到的赋值操作符：

这个运算采用实时运算的方式，将v1和v2的相应元素相加得到的和赋值给v3各自相应的元素。这就不会产生MyVector的临时对象。

然而这个程序不支持多于两个操作数的表达式运算，比如

原因是在第1次相加后，还会尝试进行第2次相加：

这个表达式需要一个重载运算符operator+（），它的第1个参数是MyVectorSum类型，第2个参数是MyVector类型。可以尝试提供多个重载来满足所有的情况，但最好的办法是让模板来做这项工作，如下面的程序所示：

使用模板参数Left和Right，这个模板很容易地引出一个和的参数类型，来代替上例中指派的那些类型。由于MyVectorSum模板持有这额外的两个参数，因此它能表示由MyVector和MyVectorSum任意组成的一对参数的和。

赋值操作符现在是一个成员函数模板。这将允许任一对＜T, N＞与任一对＜Left, Right＞结合，因此一个MyVector对象能够得到来自一个MyVectorSum对象的赋值，该MyVectorSum对象持有MyVector和MyVectorSum类型的引用，这两个类型的引用可以组成任何可能的一对。

与前面一样，可以通过跟踪一个简单的赋值操作来准确地了解这个地方发生了些什么事情，从下述表达式开始

由于结果表达式变得笨拙冗长且难于处理，在下面的解释中，我们用MVS作为MyVectorSum的缩写，并且忽略模板的参数。

第1个操作是v1+v2，这将调用内联函数operator+（），这个内联函数依次将MVS（v1，v2）插入到编译流中。然后它被相加到v3上，从而表达式MVS（MVS（v1，v2），v3）产生一个临时对象。这个完整语句的最后表达结果是：

这种转换完全由编译器安排，它也解释了为什么把这种技术冠以“表达式模板”之名。MyVectorSum模板代表了一个表达式（上例中是加法表达式），上述的嵌套调用可能也使读者回忆起左关联表达式v1+v2+v3的语法分析树。

由Angelika Langer和Klaus Kreft写的一篇优秀文章解释了这项技术如何扩展到更复杂的计算。^[11]

[1]技术上讲，这些都是编译时常值，因此可能会说其中的标识符按照习惯用法应该全是大写字母，之所以坚持用小写是因为在这里它们模拟了变量。

[2]1966年，Böhm和Jacopini证明了任意具有以下特征的语言都相当于一个图灵机：支持选择和循环，并具有使用变量随机数的能力。图灵机被认为具有表达任意算法的能力。

[3]Czarnecki和Eisenecker，《Generative Programming：Methods, Tools, and Applications》，Addison Wesley，2000，第417页。

[4]有一种更好的计算整数幂的方法：Russian Peasant算法。

[5]《Modern C++Design》，第23～26页。

[6]不允许将对象类型（除了内建的）传递给一个省略号参数特化，但是由于只是计算它的大小（一个编译时操作），实际上表达式在运行时没有被判断。

[7]在Lippman的《C++Gems》，SIGS，1996中可以找到Todd的原文的再版。它也表明了除了保留数学符号和优化的代码，表达式模板也允许在C++库中结合使用其他编程语言中的范例和机制，如Lambda表达式。另一个例子是奇特的类库Spirit，它是一个大量使用表达式模板的语法剖析器，它允许在C++中直接使用（一个近似的）EBNF符号，且产生了非常有效的语法剖析器。参看http：//spirit.sourceforge.net/。

[8]参看他和Nico的《C++Templates》，这是一本早期的权威著作。

[9]即《Blitz++》（http：//www.oonumerics.org/blitz/），《the Matrix T emplate Library》（http：//www.osl.iu.edu/research/mtl/）和《POOMA》（http：//www.acl.lanl.gov/pooma/）。

[10]指的是在数学中的“向量”，它是一个固定长度、一维的数值数组。

[11]Langer和Kreft的文章“C++Expression Templates”见2003年3月的“C/C++Users Journal”。也可以参见2003年6月同一本杂志上的由Thomas Becker发表的有关表达式模板的文章（该文章是本节内容素材的来源）。