2.2 试做一个计算器
向不了解yacc/lex的人介绍其功能的话,与其一上来就举“用yacc/lex制作编程语言”的例子,不如先从一些简单的例子讲起比较好。所以我们以一个简单的“计算器”为例做介绍。
将计算器作为yacc/lex的示例实在有些老套,但是又很实用。Windows都会预装一个带有图形界面的计算器软件,仔细想来,PC上明明有好用的键盘,却还要用鼠标去一个一个点计算器上的按钮未免有些傻 [4]。正因为Windows的计算器不好用,所以有很多人会选择使用普通的计算器。可明明眼前就摆着高性能的电脑,偏要用买来的计算器,同样也显得很奇怪,更不要说还有“附带计算器功能的鼠标垫”这种创意产品,就更加本末倒置了。无论是Windows自带的计算器,还是从日杂店买来的计算器,都从上面看不到运算符号的优先顺序,也无法直接计算带括号的式子(因为看不到前一个输入的值)。几十个数值求和时,你会不会担心万一中间输错了该怎么办?我经常会。
而我们要制作的计算器,会通过命令行方式启动,可以通过键盘输入整个算式,然后直接显示计算结果。因此可以直观地看到运算的优先顺序,比如输入
1 + 2 * 3
会得到结果7而不是9。因为能看到整个算式,所以还可以很容易地检查有没有输错。
计算器的指令名为 mycalc 。一个实际运行的例子是这样的(% 是命令提示符):
% mycalc ←启动mycalc
1+2 ←输入算式
>>3.000000 ←显示结果
1+2*3 ←乘法与加法的混合运算
>>7.000000 ←按运算优先顺序输出结果
虽然只用了整数,却输出“3.000000”这样的结果,这是因为 mycalc在内部完全使用 double进行运算。
2.2.1 lex
lex是自动生成词法分析器的工具,通过输入扩展名为 .l的文件,输出词法分析器的C语言代码。而flex则是增强版的lex,而且是免费的。
词法分析器是将输入的字符串分割为记号的程序,因此必须首先定义 mycalc所用到的记号。
mycalc所用到的记号包括下列项目:
运算符。在mycalc中可以使用四则运算,即 +、 -、 *、 /。
整数。如 123等。
实数。如 123.456等。
换行符。一个算式输入后,接着输入换行符就会执行计算,因此这里的换行符也应当设置为记号。
在lex中,使用 正则表达式 定义记号。
为 mycalc所编写的输入文件mycalc.l如代码清单2-1所示。
代码清单2-1 mycalc.l
1: %{
2: #include <stdio.h>
3: #include "y.tab.h"
4:
5: int
6: yywrap(void)
7: {
8: return 1;
9: }
10: %}
11: %%
12: "+" return ADD;
13: "-" return SUB;
14: "*" return MUL;
15: "/" return DIV;
16: "\n" return CR;
17: ([1-9][0-9]*)|0|([0-9]+.[0-9]+) {
18: double temp;
19: sscanf(yytext, "%lf", &temp);
20: yylval.double_value = temp;
21: return DOUBLE_LITERAL;
22: }
23: [ \t] ;
24: . {
25: fprintf(stderr, "lexical error.\n");
26: exit(1);
27: }
28: %%
代码第11行为 %%,此行之前的部分叫作 定义区块 。在定义区块内,可以定义初始状态或者为正则表达式命名(即使不知道正则表达式的具体内容也可以命名)等。在本例中放置了一些C代码。
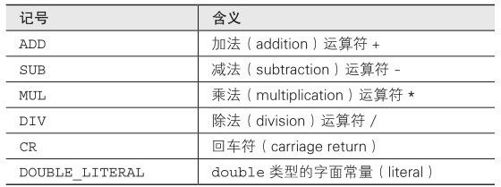
第2行至第9行,使用%{和%} 包裹的部分,是想让生成的词法分析器将这部分代码原样输出。后续程序所需的头文件 #include 等都包含在这里,比如第三行用 #include包含进来的y.tab.h头文件,就是之后yacc自动生成的头文件。下面的 ADD、 SUB、 MUL、 DIV、 CR、 DOUBLE_LITERAL等都是在y.tab.h中用 #define 定义的宏,其原始出处则定义于mycalc.y 文件中(详见2.2.3 节)。这些宏将记号的种类区分开来。顺便附上表2-1说明记号的具体含义。
表2-1 记号及其含义
第5行到第9行定义了一个名为 yywrap() 的函数。如果没有这个函数的话,就必须手动链接lex的库文件,在不同环境下编译时比较麻烦,因此最好写上。本书不会再对这个函数做深入说明,简单知道其作用,直接使用就可以了。
第12行到27行是 规则区块 。读了代码就能明白,这一部分是使用正则表达式 [5]去描述记号。
在规则区块中遵循这样的书写方式:一个正则表达式的后面紧跟若干个空格,后接C代码。如果输入的字符串匹配正则表达式,则执行后面的C代码。这里的C代码部分称为动作(action)。
在第12~16行中,会找到四则运算符以及换行符,然后通过 return返回其特征符。所谓特征符,就是上文所述在y.tab.h中用 #define定义、用来区别记号种类的代号。
之前提到了这么多次“记号”,其实我们所说的记号是一个总称,包含三部分含义,分别是:
1. 记号的种类
比如说计算器中的 123.456 这个记号,这个记号的种类是一个实数(DOUBLE_LITERAL)。
2. 记号的原始字符
一个记号会包含输入的原始字符,比如 123.456 这个记号的原始字符就是 123.456。
3. 记号的值
123.456这个记号代表的是实数123.456的值的意思。
对于 + 或 - 这样的记号来说,只需要关注其记号种类就可以了,而如果是 DOUBLE_LITERAL记号,记号的种类与记号的值都必须传递给解析器。
第17行的正则表达式,是一个匹配“数值”用的正则表达式。表达式匹配成功的结果,即上面列举的记号三要素中,“记号的原始字符”会在相应动作中被名为 yytext的全局变量(这算是lex的一个丑的设计)引用,并进一步使用第19行的 sscanf()进行解析。
动作解析出的值会存放在名为 yylval的全局变量中(又丑一次)。这个全局变量 yylval本质上是一个联合体(union),可以存放各种类型记号的值(在这个计算器程序中只有 double类型)。联合体的定义部分写在yacc的定义文件mycalc.y中。
到第28行,又出现了一次 %%。这表示规则区块的结束,这之后的代码则被称为 用户代码区块 。在用户代码区块中可以编写任意的C代码(例子中没有写)。与定义区块不同,用户代码区块无需使用 %{ %}包裹。
2.2.2 简单正则表达式讲座
lex通过正则表达式定义记号。正则表达式在Perl、Ruby语言中广泛使用,而UNIX用户也经常会在编辑器或 grep命令中接触到。本书的读者可能未必都有这样的技术背景,所以我们在本书涉及的范围内,对正则表达式做一些简单的说明。
在代码清单2-1的第17行中有这样一个正则表达式(初看可能稍微有点复杂):
([1-9][0-9]*)|0|([0-9]+.[0-9]+)
首先, [与 ]表示匹配此范围内的任意字符。而 [ ]还支持使用连接符的缩写方式。比如写 1-9与写 123456789是完全一样的。
最初圆括号中的 [1-9]代表匹配1~9中任意一个数字。其后的 [0-9]代表匹配0~9的任意一个数字。
在此之后的*,代表匹配前面的字符 [6]0次或多次。
因此, [1-9][0-9]*这个正则表达式,整体代表以 1~9 开头(只有 1位),后接 0个以上的 0~9 的字符。而这正是我们在 mycalc 中对整数所做的定义。
在表2-2中列举了若干字符串,并展示其是否匹配我们所制定的整数规则。
表2-2 字符串的匹配
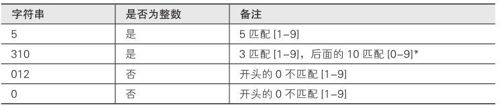
如上表所示, mycalc不会将 012这样的输入作为数值接收,这完全符合我们的预期。
但是将0也排除的话还是有问题的,程序必须能接受所有的实数。因此在正则表达式中又使用了 |。 |代表“或”的意思。
第17行的正则表达式就被修正为:
([1-9][0-9]*)|0|([0-9]+.[0-9]+)
现在应该可以明白前半段正则表达式的整体意思了,即将整数(0以外)的正则表达式与0通过 |分成两部分然后并列(加上圆括号 ()是将这部分作为一个集合才能通过 |与0并列)。
后半部分的 [0-9]+.[0-9]+ 中用到了 +。 * 是代表“匹配前面的字符0次或多次”,而 + 则是“匹配前面的字符1 次或多次”,因此这部分整体代表“0~9的数字至少出现一次,后接小数点 .后又接至少一位0~9数字”。这些与前面整合起来,共同构成了 mycalc对于实数的定义。
小数点的书写不是只写一个 .而是写成了 .,因为 .在正则表达式中有特殊的含义(后文即将介绍),所以需要使用 \转义。 [ ]、 *、 +、 .等这些在正则表达式中有特殊含义的字符称为 元字符 ,元字符可以像上文那样用 \或双引号 [8] 进行转义。代码的第12~14行,就是使用双引号转义的方法对乘法和加法的运算符进行了定义。
第23行的正则表达式 [ \t] 是对空格以及制表符进行匹配,对应动作为空,因此可以忽略每一行的空白字符。
第24行的 .会匹配任意一个字符。这里用于检测是否输入了程序不允许的字符。
首先,lex将输入的字符串分割到若干个记号中时,会尽可能选择较长的匹配。比如C语言中同时有 +运算符和 ++运算符,那么当输入 ++时,lex不会匹配为两个 +运算符,而是返回一个 ++(如果不按这个逻辑,程序很难正常工作)。如果两个规则出现同样长度的匹配时,会优先匹配前一个规则。也就是说,如果输入字符直到最后一条规则(匹配任意字符)才匹配成功的话,说明这个字符不符合前面所有的规则,是错误的输入。
在表2-3中列举了一些常用的元字符。元字符以外的字符直接书写就可以了。
表2-3 lex中正则表达式的元字符

2.2.3 yacc
yacc是自动生成语法分析器的工具,输入扩展名为 .y的文件,就会输出语法分析器的C语言代码。bison则是GNU项目所发布的yacc的功能扩充版。
mycalc中yacc的输入文件mycalc.y如代码清单2-2所示。
代码清单2-2 mycalc.y
1: %{
2: #include <stdio.h>
3: #include <stdlib.h>
4: #define YYDEBUG 1
5: %}
6: %union {
7: int int_value;
8: double double_value;
9: }
10: %token <double_value> DOUBLE_LITERAL
11: %token ADD SUB MUL DIV CR
12: %type <double_value> expression term primary_expression
13: %%
14: line_list
15: : line
16: | line_list line
17: ;
18: line
19: : expression CR
20: {
21: printf(">>%lf\n", $1);
22: }
23: expression
24: : term
25: | expression ADD term
26: {
27: $$ = $1 + $3;
28: }
29: | expression SUB term
30: {
31: $$ = $1 - $3;
32: }
33: ;
34: term
35: : primary_expression
36: | term MUL primary_expression
37: {
38: $$ = $1 * $3;
39: }
40: | term DIV primary_expression
41: {
42: $$ = $1 / $3;
43: }
44: ;
45: primary_expression
46: : DOUBLE_LITERAL
47: ;
48: %%
49: int
50: yyerror(char const *str)
51: {
52: extern char *yytext;
53: fprintf(stderr, "parser error near %s\n", yytext);
54: return 0;
55: }
56:
57: int main(void)
58: {
59: extern int yyparse(void);
60: extern FILE *yyin;
61:
62: yyin = stdin;
63: if (yyparse()) {
64: fprintf(stderr, "Error ! Error ! Error !\n");
65: exit(1);
66: }
67: }
第1~5行与lex相同,使用 %{%}包裹了一些C代码。
第4行有一句 #define YYDEBUG 1,这样将全局变量 yydebug设置为一个非零值后会开启Debug模式,可以看到程序运行中语法分析的状态。我们现在还不必关心这个。
第6~9行声明了记号以及 非终结符 的类型。正如前文所写,记号不仅需要包含类型,还需要包含值。记号可能会有很多类型,这些类型都声明在集合中。本例中为了方便说明,定义了一个 int类型的 int_value和 double类型的 double_value,不过目前还没有用到 int_value。
非终结符是由多个记号共同构成的,即代码中的 line_list、 line、expression、 term这些部分。为了分割非终结符,非终结符最后都会以一个特殊记号结尾。这种记号称作 终结符 。
第10~11行是记号的声明。 mycalc 所用到的记号类型都在这里定义。 ADD、 SUB、 MUL、 DIV、 CR 等记号只需要包含记号的类型就可以了,而值为 DOUBLE_LITERAL 的记号,其类型被指定为 <double_value>。这里的 double_value是来自上面代码中 %union集合的一个成员名。
第12行声明了非终结符的类型。
与lex一样,13行的 %%为分界,之后是 规则区块 。yacc的规则区块,由 语法规则 以及C语言编写的相应动作两部分构成。
在yacc中,会使用类似BNF(巴科斯范式,Backus Normal Form)的规范来编写语法规则。
计算器程序因为规则部分中混杂了动作,阅读起来有点难度,所以在代码清单2-3中,仅仅将规则部分抽出,并加入了注释。
代码清单2-3 计算器的语法规则
1: line_list / 多行的规则 /
2: : line / 单行 /
3: | line_list line / 或者是一个多行后接单行 /
4: ;
5: line / 单行的规则 /
6: : expression CR / 一个表达式后接换行符 /
7: ;
8: expression / 表达式的规则 /
9: : term / 和项 /
10: | expression ADD term / 或 表达式 + 和项 /
11: | expression SUB term / 或 表达式 - 和项 /
12: ;
13: term / 和项的规则 /
14: : primary_expression / 一元表达式 /
15: | term MUL primary_expression /或和项 一元表达式 */
16: | term DIV primary_expression /或和项 /一元表达式 /
17: ;
18: primary_expression / 一元表达式的规则 /
19: : DOUBLE_LITERAL / 实数的字面常量 /
20: ;
为了看得更清楚,可以将语法规则简化为下面的格式:
A
: B C
| D
;
即A的定义是B与C的组合,或者为D。
第1~4行的书写方式,是为了表示该语法规则在程序中可能会出现一次以上。在 mycalc中,输入一行语句然后敲回车键后就会执行运算,之后还可以继续输入语句,所以需要设计成支持出现一次以上的模式。
另外,请注意在上面的计算器的语法规则中,语法规则本身就包含了运算符的优先顺序以及结合规律。如果不考虑运算符的优先顺序(乘法应该比加法优先执行),上文的语法规则应该写成这样。
expression / 表达式的规则 /
: primary_expression / 一元表达式 /
| expression ADD expression / 或 表达式 + 表达式 /
| expression SUB expression / 或 表达式 - 表达式 /
| expression MUL expression / 或 表达式 表达式 */
| expression DIV expression / 或 表达式 / 表达式 /
;
primary_expression / 一元表达式的规则 /
: DOUBLE_LITERAL / 实数的字面常量 /
;
那么在这样的语法规则下,yacc是如何运作的呢?我们以代码清单2-3为例一起来看看吧。
大体上可以这样说,yacc所做的工作,可以想象成一个类似“俄罗斯方块”的过程。
首先,yacc生成的解析器会保存在程序内部的栈,在这个栈中,记号就会像俄罗斯方块中的方块一样,一个个堆积起来。
比如输入1 + 2 * 3,词法分析器分割出来的记号(最初是 1)会由右边进入栈并堆积到左边。

像这样一个记号进入并堆积的过程,叫作移进(shift)。
mycalc 所有的计算都是采用 double 类型,所以记号 1 即是 DOUBLE_LITERAL。当记号进入的同时,会触发我们定义的规则:
primary_expression
: DOUBLE_LITERAL
然后记号会被换成 primary_expression。

类似这样触发某个规则并进行置换的过程,叫作 归约 (reduce)。primary_expression将进一步触发规则:
term
: primary_expression
然后归约为 term。

再进一步根据规则:
expression
: term
最终被归约为一个 expression。

接下来,记号 +进入。在进入过程中,由于没有匹配到任何一个规则,所以只好老老实实地进行移进而不做任何归约。

接下来是记号 2进入。

经过上述同样的规则,记号 2(DOUBLE_LITERAL)会经过 primary_expression被归约为 term。

这里记号 2本应该匹配到如下的规则:
expression
| expression ADD term
yacc和俄罗斯方块一样,可以预先读取下一个要进入的记号,这里我们就可以知道下一个进入的会是 *,因此应当考虑到记号 2会匹配到 term规则的可能性。
term
| term MUL primary_expression
归约完毕后再一次移进。
接下来记号 3进入,

被归约为 primary_expression后,
term、 *、 primary_expression这一部分将匹配规则:
term
| term MUL primary_expression
被归约为 term。

之后, expression、 +、 term又会匹配规则
expression
| expression ADD term
最终被归约为 expression。

每次触发归约时,yacc都会运行该规则的相应动作。比如乘法对应执行的规则如下文所示。
34: term
36: | term MUL primary_expression
37: {
38: $$ = $1 * $3;
39: }
动作是使用C语言书写的,但与普通的C语言又略有不同,掺杂了一些 $$、 $1、 $3之类的表达式。
这些表达式中, $1、 $3的意思是分别保存了 term与 primary_expression的值。即yacc输出解析器的代码时,栈中相应位置的元素将会转换为一个能表述元素特征的数组引用。由于这里的 $2是乘法运算符(*),并不存在记号值,因此这里引用 $2的话就会报错。
$1与 $3进行乘法运算,然后将其结果赋给 $$,这个结果值将保留在栈中。在这个例子中,执行的计算为 2 * 3,所以其结果值 6会保留在栈中(如图2-3)。

图2-3 归约发生时栈的动作
咦, $1与 $3对应的应该是 term和 primary_expression,而不是2与3这样的 DOUBLE_LITERAL数值才对呀,为什么会作为2*3来计算呢?
可能会有人提出上面的疑问吧。这是因为如果没有书写动作,yacc会自动补全一个 { $$ = $1 } 的动作。当 DOUBLE_LITERAL 被归约为 primary_expression、 primary_expression 被 归 约 为 term 的 时 候, DOUBLE_LITERAL包含的数值也会被继承。
34: term
35: : primary_expression
{
$$ = $1; / 自动补全的动作 /
}
…
45: primary_expression
46: : DOUBLE_LITERAL
{
$$ = $1; / 自动补全的动作 /
}
$$与 $1的数据类型,分别与其对应的记号或者非终结符的类型一致。比如, DOUBLE_LITERAL对应的记号被定义为:
9: %token <double_value> DOUBLE_LITERAL
expression、 term、 primary_expression的类型则为:
11: %type <double_value> expression term primary_expression
这里的类型被指定为 <double_value>,其实是使用了在 %union部分声明的联合体中的 double_value成员。
由于我们以计算器为例,计算器的动作会继续计算得出的值,但仅靠这些还不足以制作编程语言。因为编程语言中都会包含简单的循环,而语法分析只会运行一次,所以动作还要支持循环处理同一处代码才行。
因此在实际的编程语言中,会从动作中构建分析树。这部分处理的方法会在后面的章节中介绍。
2.2.4 生成执行文件
接下来,让我们实际编译并链接计算器的源代码,生成执行文件吧。
在标准的UNIX中,按顺序执行下面的指令(%是命令行提示符),就会输出名为mycalc的执行文件。
% yacc -dv mycalc.y ←运行yacc
% lex mycalc.l ←运行lex
% cc -o mycalc y.tab.c lex.yy.c ←使用C编译器编译
如果在Windows的环境下,参考1.6.1节中的说明,需要安装gcc、bison、flex,然后运行下面的指令(C:\Test>是命令行提示符)。
C:\Test>bison —yacc -dv mycalc.y ←用bison代替yacc并运行
C:\Test>flex mycalc.l ←运行flex
C:\Test>gcc -o mycalc y.tab.c lex.yy.c ←使用C编译器编译
这个过程中会生成若干文件。其流程以图片表示的话,如图2-4所示。
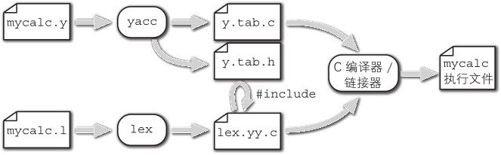
图2-4 yacc/lex的编译
y.tab.c中包含yacc生成的语法分析器的代码,lex.yy.c是词法分析器的代码。为了将mycalc.y中定义的记号及联合体传递给lex.yy.c,yacc会生成y.tab.h这个头文件。
此外,作为C语言程序当然要有 main()函数,在mycalc中 main()位于mycalc.y的用户代码区块(第49行以后),最终编译器会负责合并代码,所以这里的 main()与其他.c文件分离也不要紧。在 main()函数中的全局变量 yyin可以设定输入文件,调用 yyparse()函数。
由于我们使用bison替代了yacc,默认生成的文件就不是y.tab.c和y.tab.h,而是mycalc.tab.c和mycalc.tab.h。所以在上例中添加了—yacc参数,可以让bison生成与yacc同名的文件。本书为了统一,bison会始终带上 —yacc参数。
2.2.5 理解冲突所代表的含义
实际用yacc试做一下解析器,可能会被 冲突 (conflict)问题困扰。所谓冲突,就是遇到语法中模糊不清的地方时,yacc报出的错误。
比如C语言的if语句,就很明显有语法模糊问题。
if (a == 0)
if (b == 0)
printf(在这里a与b都为0\n);
else
printf(这里是a非0?错!\n);
上面的代码中,我们不清楚最后的 else 对应的究竟是哪一个 if,这就是冲突。
yacc运行时,遇到下面任意一种情况都会发生冲突。
同时可以进行多个归约。
满足移进的规则,同时又满足归约的规则。
前者称为归约/归约(reduce/reduce)冲突,后者称为移进/归约(shift/reduce)冲突。
即便发生冲突,yacc仍然会生成解析器。如果存在归约/归约冲突,则优先匹配前面的语法规则,移进/归约冲突会优先匹配移进规则。很多书会写归约/归约冲突是致命错误,而移进/归约冲突则允许,这两者的确是存在严重程度的差别,但是在我来看,无论发生哪一种冲突都是难以容忍的,我恨不得消灭代码中所有的冲突问题。
yacc运行时可以附带 -v参数,标准yacc会生成y.output文件(bison则会将输入文件名中的扩展名.y替换为.output并生成)。
这个y.output文件会包含所有的语法规则、解析器、所有可能的分支状态以及编译器启动信息。
那么我们实际做出一个冲突,然后观察一下y.output文件吧。
将代码清单2-2中的语法规则
23: expression
24: : term
25: | expression ADD term ←将这里的ADD
更改为下文所示:
23: expression
24: : term
25: | expression MUL term ←更改为MUL
变更后会产生3个移进/归约冲突。
% yacc -dv mycalc.y
conflicts: 3 shift/reduce
然后再看y.output文件。
根据yacc或bison的版本与语言设置,y.output的输出会有微妙的区别。这里以bison2.3英文模式为例(为了节约纸张将空行都去掉了)。日语环境下,“Grammar”会变成“文法”等,错误信息也都会显示为日语。
总体来说,y.output文件的前半部分看起来基本都会是下面这个样子(代码清单2-4)。
代码清单2-4 y.output(前半部分)
Terminals which are not used ←没有使用ADD的警告
ADD
State 5 conflicts: 1 shift/reduce ←冲突信息(见下文)
State 14 conflicts: 1 shift/reduce
State 15 conflicts: 1 shift/reduce
Grammar
0 $accept: line_list $end
1 line_list: line
2 | line_list line
3 line: expression CR
4 expression: term
5 | expression MUL term
6 |expression SUB term
7 term: primary_expression
8 | term MUL primary_expression
9 | term DIV primary_expression
10 primary_expression: DOUBLE_LITERAL
首先将 ADD改为 MUL后,开头会出现“ADD没有被使用”的警告。下面会有3行冲突信息,此处后文会细说。再后面的“Grammar”跟着的是mycalc.y中定义的语法规则。
mycalc.y中可以使用 |(竖线,表示或)书写下面这样的语法规则:
line_list : line
| line_list line
实际上与下面这种写法的语法规则是完全一样的。
line_list : line
line_list : line_list line
y.output文件中,会给每一行规则附上编号。
上面的规则0,是yacc自动附加的规则, $accept代表输入的内容, $end代表输入结束,目前还不需要特别在意这个问题。
y.output文件的后半部分会将解析器可能遇到的所有“状态”全部列举出来(代码清单2-5)。
代码清单2-5 y.output(后半部分)
state 0
0 $accept: . line_list $end
DOUBLE_LITERAL shift, and go to state 1
line_list go to state 2
line go to state 3
expression go to state 4
term go to state 5
primary_expression go to state 6
state 1
10 primary_expression: DOUBLE_LITERAL .
$default reduce using rule 10 (primary_expression)
state 2
0 $accept: line_list . $end
2 line_list: line_list . line
$end shift, and go to state 7
DOUBLE_LITERAL shift, and go to state 1
line go to state 8
expression go to state 4
term go to state 5
primary_expression go to state 6
state 3
1 line_list: line .
$default reduce using rule 1 (line_list)
state 4
3 line: expression . CR
5 expression: expression . MUL term
6 | expression . SUB term
SUB shift, and go to state 9
MUL shift, and go to state 10
CR shift, and go to state 11
下略
前文中有一个俄罗斯方块的比喻,读者通过那个比喻可能会这样理解:解析器在一个记号进入栈后,从栈的开头一个字符一个字符扫描,如果发现这个记号满足已有的某个规则,就去匹配该规则。但其实这样做会让编译器变得很慢。
现实中,yacc在生成解析器的阶段,就已经将解析器所能遇到的所有状态都列举出来,并做成了一个解析对照表(Parse Table),表中记录了“状态A下某种记号进入后会转换到状态B”这样的映射关系,y.output的后半部分就罗列了所有可能的映射关系。听说这有点像麻将中的听牌,不过因为我不玩麻将,所以也不是很清楚。
有了这些列举出的状态,当记号进入后,就可以很容易找到在何种状态下移进,或者根据何种规则归约。那么对于之前我们故意做出的冲突,在我的环境下,y.output开头会输出如下信息:
State 5 conflicts: 1 shift/reduce
State 14 conflicts: 1 shift/reduce
State 15 conflicts: 1 shift/reduce
可以看到state 5引起了冲突,我们来看一下:
state 5
4 expression: term .
8 term: term . MUL primary_expression
9 | term . DIV primary_expression
MUL shift, and go to state 12
DIV shift, and go to state 13
MUL [reduce using rule 4 (expression)]
$default reduce using rule 4 (expression)
上例中,第一行的 state 5即为状态的编号,1个空行后接下来的3行是y.output前半部分中输出的语法规则(语法规则还附加了编号)。语法规则中间有 .,代表记号在当前规则下能被转换到哪个程度。比如state 5这个状态下,记号最多被转换为 term,然后需要等待下一个记号进行归约。
再空一行,接下来记录的是当前状态下,下一个记号进入时将如何变化。具体来讲,这里当 MUL(*)记号进入后会进行移进并转换为state 12。如果进入的是 DIV(/),则同样进行移进并转移到state 13。
再经过1个空行后下一行是:
MUL [reduce using rule 4 (expression)]
意思是当 MUL 进入后,可以按照规则 4 进行归约。这也就是移进 / 归约冲突。
yacc 默认移进优先,所以 MUL 进入后会转移到状态12。在y.output 中state 12是这样的:
state 12
8 term: term MUL . primary_expression
DOUBLE_LITERAL shift, and go to state 1
primary_expression go to state 16
而如果是归约的情况,所要参照的规则4是这样的:
4 expression: term
也就是说,当记号被转换为term 后,下一个记号 进入以后,yacc 会报告有冲突发生,冲突的原因是当前term既可以继续进行移进,也可以归约为expression并结束。而这正是由于我们将 ADD修改为 MUL后, 的运算优先级被降低而引发的混乱。
对y.output阅读方法的说明就此告一段落,其实在实践中想要探明冲突原因并解决冲突,是比较有难度的。
因此即便表面上看起来都一样的编程语法,根据语法规则的书写方式不同, yacc可能报冲突也可能不报冲突(可以参考后文讲到的LALR(1)语法规定)。比如本节开头所说的C语言中 if else语法模糊的问题,在Java中就从语法规则入手回避了这个冲突。而类似这样的小问题以及相应的解决“窍门”,在自制编程语言中数不胜数,所以从现实出发,模仿已有的编程语言时,最好也要多多参考其语法规则。
2.2.6 错误处理
前面的小节中介绍了如何应对语法规则中的冲突问题,即编译器制作阶段的错误处理。而在自制编程语言时,还要考虑到使用这门语言编程的人如果犯了错误该怎么办。
在稍微旧一点的编译器书籍中,常常能读到下面这样的文字。
让用户自己不断的编译,既浪费CPU资源也浪费时间,因此编译器最好只经过一次编译就能看到大部分错误信息。
但是程序中的一个错误,其原因可能是由于其他错误引起的(可能会引起错误信息的雪崩现象)。一边不希望无用的错误信息出现,一边又想尽可能多地显示错误的原因,这其中的平衡点是很难掌握的。
然而时至今日,CPU已经谈不上什么“浪费资源”了,因为在多数情况下,编译过程往往一瞬间就能结束。那么即便一次编译显示出很多错误信息,用户一般也只会看第一条(我就是这样),这样的话,“编译器最好只经过一次编译就能看到大部分错误信息”也就没什么意义了。
所以最省事的解决方法之一就是,一旦出错,立即使用 exit()退出。之后章节中的crowbar和Diksam都是这样处理的。
但是对于计算器来说,是需要与用户互动,如果输错了一点程序就强制退出的话,对用户也太不友好了。
因此我们可以利用yacc的功能实现一个简单的错误恢复机制。
首先在mycalc.y的非终结符 line的语法规则中,追加下面的部分。
line
: expression CR
{
printf(">>%lf\n", $1);
}
| error CR
{
yyclearin;
yyerrok;
}
;
这里新出现的是 error记号。 error记号是匹配错误的特殊记号。 error可以后接 CR(换行符),这样书写可以匹配包含了错误的所有记号以及行尾。
动作中的 yyclearin会丢弃预读的记号,而 yyerrok则会通知yacc程序已经从错误状态恢复了。
既然是有交互的工具,一般都会使用换行来分割每次的会话,每一个错误信息后加上换行符应该会显得更美观吧。
