2.5 习题:扩展计算器
2.5.1 让计算器支持括号
如果要说普通计算器有什么不方便的地方,不能直接输入括号进行计算就是其中之一。因此为了让 mycalc支持括号,我做了一些修改。
因为使用的是yacc/lex,所以首先在lex中增加 (和 )两个记号。
(前略)
"+" return ADD;
"-" return SUB;
"*" return MUL;
"/" return DIV;
"(" return LP; ←新增
")" return RP; ←新增
"\n" return CR;
(后略)
LP、 RP分别是left paren、right paren的缩写。
然后将 primary_expression的语法规则替换为下面这样:
primary_expression
: DOUBLE_LITERAL
| LP expression RP
{
$$ = $2;
}
;
一看就能明白,意思是被 ( ) 包裹的 expression 还是一个 primary_expression。
不过仅这两处修改还不能让 mycalc支持括号。
使用递归下降分析法制作语法分析器的话, primary_expression的语法图需更改为图2-6那样。
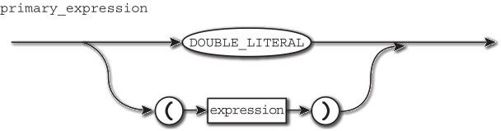
图2-6 在语法图中引入括号
这表示用括号将 expression 包裹的部分,整体将会作为 primary_expression来处理。
那么按这个思路重新编写parser.c如下所示。
1: static double
2: parse_primary_expression()
3: {
4: Token token;
5: double value;
6:
7: my_get_token(&token);
8: if (token.kind == NUMBER_TOKEN) {
9: return token.value;
10: } else if (token.kind == LEFT_PAREN_TOKEN) {
11: value = parse_expression();
12: my_get_token(&token);
13: if (token.kind != RIGHT_PAREN_TOKEN) {
14: fprintf(stderr, "missing ')' error.\n");
15: exit(1);
16: }
17: return value;
18: } else {
19: unget_token(&token);
20: return 0.0; / make compiler happy /
21: }
22: }
将语法图直接转换为代码应该不是很难,只要按图中的思路去做即可。如果进入的不是 DOUBLE_LITERAL 而是 (,则把括号中的部分作为一个 expression去解析就可以了。此外,如果 expression解析完毕后没有找到标记结束的右括号 ),则需要报错。
2.5.2 让计算器支持负数
其实目前做出来的计算器,还无法支持负数。因为在定义数值时用的正则表达式是 [1-9][0-9]或 [0-9].[0-9]*,根本没有把负数作为一种数值考虑进来。
那么,如果我们想修改计算器让其支持负数,要怎么办呢?
可能有人会想,只要在词法分析器中将 -5 这样的输入也作为 DOUBLE_LITERAL 来处理不就行了吗?按这种思路, 3-5 这样的输入会被解析成 3 和 -5两个记号(请参考2.1节中的补充知识)。
因此,如果不想将负数作为记号处理,就应该在语法分析器中想办法。
如果用yacc的话,我们可能首先会想到这样做:
primary_expression
: DOUBLE_LITERAL
| SUB DOUBLE_LITERAL ←DOUBLE_LITERAL之前带“-”的部分也解析为表达式
{
$$ = -$2;
}
(下面省略)
确实,用这种方法可以给定值的实数加上负号 -。
但是,用这种方法给 -(3 * 2)这样带括号的算式再加上负号是办不到的(有人可能觉得办不到也无所谓,请允许我吹毛求疵一下)。为了再支持这种括号的处理,还需要这样修改:
primary_expression
: DOUBLE_LITERAL
| SUB primary_expression
{
$$ = -$2;
}
(下面省略)
那么在递归下降分析法中,可以允许负号的语法图如图2-7所示(这个语法图还包含了对括号的支持)。
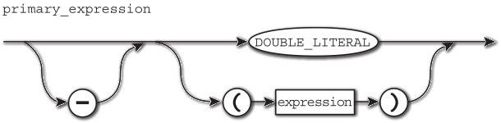
图2-7 包含负号的语法图
将其转换为代码,如下所示。
1: static double
2: parse_primary_expression()
3: {
4: Token token;
5: double value = 0.0;
6: int minus_flag = 0;
7:
8: my_get_token(&token);
9: if (token.kind == SUB_OPERATOR_TOKEN) {
10: minus_flag = 1;
11: } else {
12: unget_token(&token);
13: }
14:
15: my_get_token(&token);
16: if (token.kind == NUMBER_TOKEN) {
17: value = token.value;
18: } else if (token.kind == LEFT_PAREN_TOKEN) {
19: value = parse_expression();
20: my_get_token(&token);
21: if (token.kind != RIGHT_PAREN_TOKEN) {
22: fprintf(stderr, "missing ')' error.\n");
23: exit(1);
24: }
25: } else {
26: unget_token(&token);
27: }
28: if (minus_flag) {
29: value = -value;
30: }
31: return value;
32: }
注 释
[1]. 严格讲,包含代码中所有记号的叫作分析树或语法树,将一些无用记号剔除的才叫作抽象语法树,本书中并没有特意区分。
[3]. 最近这样的例子还有Ruby 的 VM 的 YARV,即“ Yet Another Ruby VM”的缩写,还有YAML起初也是叫作“Yet Another Markup Language”。
[4]. Windows的计算器支持使用键盘输入,但是有很多初级用户并不知道这个功能,仍然用鼠标点击。此外一些迷你键盘去掉了数字键盘区域,在上面使用计算器很不方便。 ——译者注
[6]. 因为后面还会有 [0-9]*这样的写法,所以严格讲,“匹配前面的字符”其实是“匹配前面的表达式”。
[8]. 正则表达式有很多不同的风格,lex所使用的风格支持使用双引号转义元字符,而常用的PCRE风格则只支持反斜线转义。 ——译者注
[9]. 按本书所采用的命名规范,文件内的 static变量需要附带前缀 st_。请参考3.2.1节。
[10]. 数值可以分为整数部分、小数点和小数部分。使用lex时,用一个正则表达式描述其特征,之后全部交给lex处理。而在这里我们就只能自力更生了。
[11]. 这里的例子仅限于BASIC的旧版本,在N88-BASIC 中 IFA 的写法也是不允许的。
[13]. 即被称为“C语言圣经”的The C Programming Language一书,作者名缩写为K&R[2]。中文版为《C程序设计语言(第2版·新版)》,机械工业出版社于2004年出版。
