前　言

在参与编写完优能中学高一、高二进步可视化教材（vps）后，其实我们一直都想编写一本关于高考数学复习的书．这次借着南昌新东方学校高中数学高考教研组集体的力量，结合前几年的高考教学经验，我们对高考数学的几大板块（函数与导数、三角函数与向量、数列与立体几何、解析几何与极坐标）的考点和知识进行了综合的整理，主要甄选了2011—2016年全国各省高考真题作为例题和练习，进行考点的专题讲解，编成了此套“高考数学考点全析”系列丛书，包括：《高考数学考点全析函数与导数》《高考数学考点全析数列与立体几何》《高考数学考点全析三角函数与向量》和《高考数学考点全析解析几何》．为了配合2015—2016年全国大部分省份高考数学大势所趋的考纲，本系列书的考点主要针对全国新课标考纲．

首先，来讲讲我对高考数学复习的看法吧．要想真正达到做题时的游刃有余，必须要从数学题目的编写开始认识，我用一个词来描述它就是：“编程”．这也正说明了为什么题目是永远刷不完的．其实每一个板块的考点的条件形式是有限的，这些条件可以组成一个“库”，每个题目就是从这些“条件库”中随机地编程．根据排列组合的知识，我们知道如果库中有n 个条件，

那么这n 个条件随机组合将产生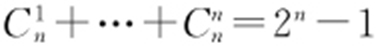 个相关的题目，这样你就会发现每个板块的题量基本都是以万为单位的，所以我们其实需要掌握的就是学会如何“翻译”这些条件．掌握了这个技巧，也就基本可以解决这类考点的相关题目了，而不是利用有限的时间盲目去刷那无穷多个题目．

比如，复习函数时，我们会发现做题时经常碰到的函数基本都是复杂函数，很少有简单函数，而教材中学习的并不是复杂函数．没有最复杂的函数，只有更复杂的函数，因此不可能通过学习复杂函数的方式来学习函数，那么我们就需要去了解复杂函数的构成．复杂函数基本可以分成两类：一类是简单函数通过平移、伸缩、翻折变成复杂函数；另一类是多个简单函数通过加减、乘除、复合变成复杂函数，所以我们可以学习几种最简单的基本初等函数，再学习它的平移、伸缩、翻折、加减、乘除、复合过程，最后达到对任何函数都有一个清楚的认识．

所以不管是哪个板块，在学习时都必须了解题目背后隐含的条件形式，学会“翻译”成数学语言（方程），这才是撒手锏．

本书的主要内容是解析几何、参数方程与极坐标．在2016年出台的高考政策改革，删掉平面几何的选做，也侧面告知了，选做题部分的解析几何相关的参数方程与极坐标基本成为了必选题（相对来说计算量小），而解析几何的两个关键点就是“翻译”和计算．本书中的例题将题目文字“翻译”成条件的过程，是要重点掌握的，再加上计算的训练（练习和真题必刷题），必能让很多受这一板块困扰的同学们得到解脱．

本书的主要结构是按“考点-例题-练习-真题”的形式，每一个考点中的例题都是按照考点 条件的形式来选择的，所以会有若干例题，选择的题源以真题为主，也有模拟题．练习与例题考点的配套性是本书的一大特点，它能帮助同学们及时反馈考点掌握情况；“真题必刷题”部分选用的是最近两年的高考真题，它的设计初衷是希望各位同学在完成对应考点的复习巩固后，可以完成近两年高考真题的考点识别，毕竟贴近高考的最好方法，就是让同学们了解最近两年该板块的整体考点情况，所以大家除了完成它以外，必要过程就是对这个板块的高频考点有一个总结．

非常感谢选择使用本书来复习高考数学的同学们，也希望通过本书可以帮到很多对解析几何板块有恐惧心理的同学们．

如果你有疑惑或感兴趣，请关注微信公众号：ncxdf高中数学，也可加入高考数学透析分享QQ群：590948624．

编　者

2016年10月