第4章 双曲线
1.定义:动点到两定点距离之差的绝对值等于定值且小于两定点距离时的 轨迹称为双曲线.即||MF 1 |-|MF 2 ||=2a ,2a <|F 1 F 2 |.
这两个定点称为双曲线的焦点 ,两焦点的距离称为双曲线的焦距 .
特别地:
①当||MF 1 |-|MF 2 ||=2a (2a =|F 1 F 2 |)时,表示点M 的轨迹为两条射线“-∞F 1 ”,“F 2 +∞” ;
②当||MF 1 |-|MF 2 ||=2a (2a >|F 1 F 2 |)时,表示点M 的轨迹不存在 .
2.双曲线的几何性质.
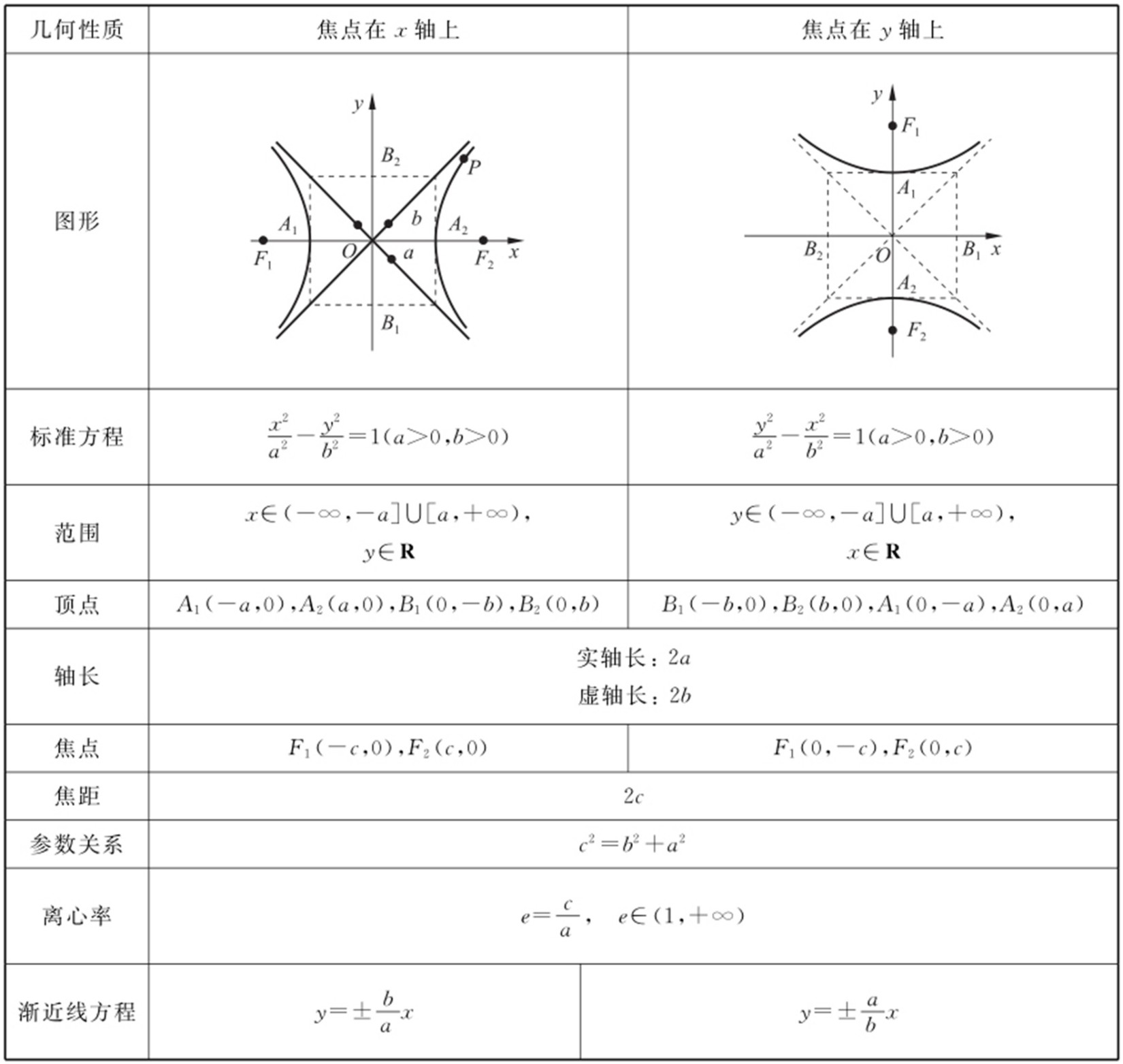
考点1 双曲线的定义
例题
【例1 】(2014·江西模考) 设圆C 与两圆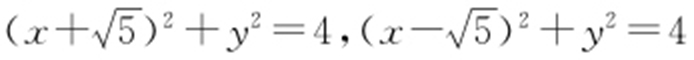 中的一个内切,另一个外切.则C 的圆心轨迹L 的方程为 .
中的一个内切,另一个外切.则C 的圆心轨迹L 的方程为 .
条件 外切⇒|O 1 O 2 |=r 1 +r 2 ,内切⇒|O 1 O 2 |=|r 1 -r 2 |.
解析 设C 的圆心为M (x ,y ),半径为r .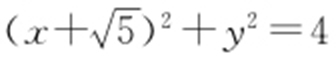 的圆心为
的圆心为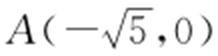 ,r 1 =2;
,r 1 =2;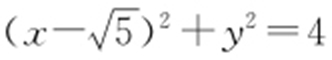 的圆心为
的圆心为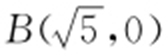 ,r 2 =2.则
,r 2 =2.则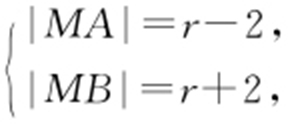 所以|MB |-|MA |=4.
所以|MB |-|MA |=4.
所以点M 的轨迹为以A ,B 为焦点的双曲线,且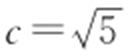 ,a =2,b 2 =1,故L 的方程为
,a =2,b 2 =1,故L 的方程为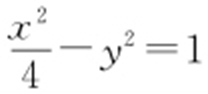 .
.
【例2 】(2014·成外测验) 平面直角坐标系xOy 中,已知双曲线 上一点M 的横坐标为3,则点M 到此双曲线的右焦点的距离为 .
上一点M 的横坐标为3,则点M 到此双曲线的右焦点的距离为 .
条件 求出点M ,利用两点距离.
解析 设M (3,y ),有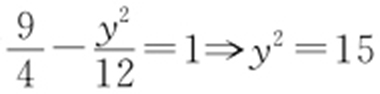 ,而右焦点为(4,0),故其
,而右焦点为(4,0),故其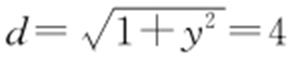 .
.
【例3 】(2009·辽宁模考) 已知F 是双曲线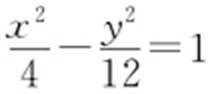 的左焦点,A (1,4),P 是双曲线右支上的动点,则|PF |+|PA |的最小值为 .
的左焦点,A (1,4),P 是双曲线右支上的动点,则|PF |+|PA |的最小值为 .
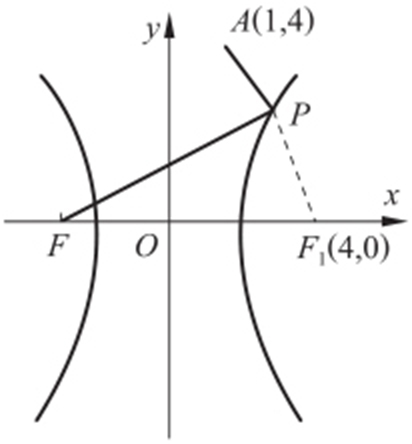
条件 利用动点P 到两焦点距离之差为2a .三点共线时两距离之和最小.
解析 因为|PF |-|PF 1 |=2a ,所以|PF |=2a +|PF 1 |=4+|PF 1 |,所以|PF |+|PA |=|PA |+|PF 1 |+4,则当|PF |+|PF 1 |取最小值时,A ,P ,F 1 三点共线,所以(|PF |+|PA |)min =|AF 1 |+4=9.
【例4 】(2012·大纲文理·8) 已知F 1 ,F 2 为双曲线C :x 2 -y 2 =2的左、右焦点,点P 在C 上,|PF 1 |=2|PF 2 |,则cos∠F 1 PF 2 =( ).
条件 |PF 1 |-|PF 2 |=2a ,且利用余弦定理.
解析 因为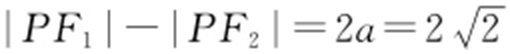 ,所以
,所以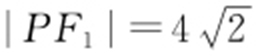 ,
, .又|F 1 F 2 |=4,则
.又|F 1 F 2 |=4,则 .故选:C.
.故选:C.
总结
(1)内切、外切为圆心距与两半径之间的关系.
(2)双曲线上一点P ,恒有||PF 1 |-|PF 2 ||=2a .
(3)熟练余弦定理.
练习
1.(2014·大纲理·9) 已知双曲线C 的离心率为2,焦点为F 1 ,F 2 ,点A 在C 上,若|F 1 A |=2|F 2 A |,则cos∠AF 2 F 1 =( ).
2.(2016·江西师大附中月考) P 为双曲线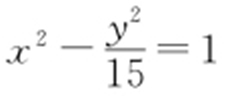 右支上一点,M ,N 分别是圆(x +4)2 +y 2 =4和(x -4)2 +y 2 =1上的点,则|PM |-|PN |的最大值为 .
右支上一点,M ,N 分别是圆(x +4)2 +y 2 =4和(x -4)2 +y 2 =1上的点,则|PM |-|PN |的最大值为 .
考点2 双曲线方程
例题
【例1 】(2011·安徽文理·2) 双曲线2x 2 -y 2 =8的实轴长是( ).
条件 双曲线标准方程.
解析 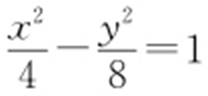 ,则实轴长为2a =4.故选:C.
,则实轴长为2a =4.故选:C.
【例2 】(2013·广东理·7) 已知中心在原点的双曲线C 的右焦点为F (3,0),离心率等于 ,则双曲线C 的方程是( ).
,则双曲线C 的方程是( ).
条件 双曲线标准方程;离心率为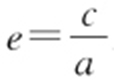 .
.
解析 由题意知,双曲线方程可设为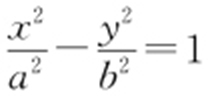 (a >0,b >0),有
(a >0,b >0),有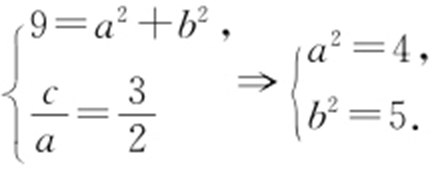 故选:B.
故选:B.
总结
双曲线的标准方程设定中a ,b ,c 的关系式为a 2 +b 2 =c 2 .
练习
1.(2011·上海理·3) 设m 为常数,若点F (0,5)是双曲线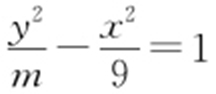 的一个焦点,则m = .
的一个焦点,则m = .
2.(2013·湖北理·5)已知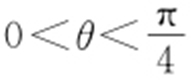 ,则双曲线C 1 :
,则双曲线C 1 :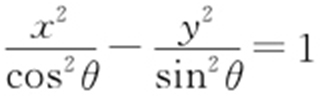 与C 2 :
与C 2 :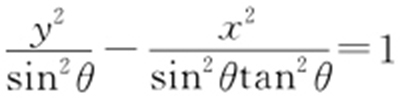 的( ).
的( ).
A.实轴长相等
B.虚轴长相等
C.焦距相等
D.离心率相等
考点3 双曲线的一般方程
例题
【例1 】(2014·新余中宜春中学联考文) 若方程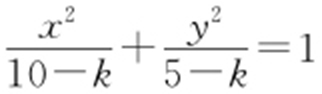 表示双曲线,则k 的取值范围是( ).
表示双曲线,则k 的取值范围是( ).
A.(5,10)
B.(-∞,5)
C.(10,+∞)
D.(-∞,5)∪(10,+∞)
条件  .
.
解析 (10-k )(5-k )<0⇒(k -5)(k -10)<0⇒5<k <10.故选:A.
【例2 】(2016·新课标1理·5) 已知方程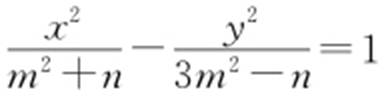 表示双曲线,且该双曲线两焦点间的距离为4,则n 的取值范围是( ).
表示双曲线,且该双曲线两焦点间的距离为4,则n 的取值范围是( ).
条件  .
.
解析 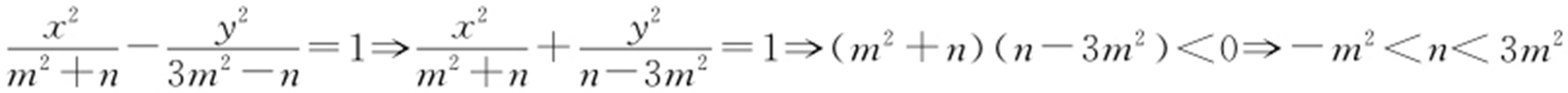 ,则此双曲线的焦点在x 轴上,有a 2 =m 2 +n ,b 2 =3m 2 -n ,所以c 2 =4m 2 =4,即m 2 =1,则-1<n <3.故选:A.
,则此双曲线的焦点在x 轴上,有a 2 =m 2 +n ,b 2 =3m 2 -n ,所以c 2 =4m 2 =4,即m 2 =1,则-1<n <3.故选:A.
总结
(1)双曲线满足mn <0.
(2)c 2 =a 2 +b 2 .
练习
(2014·吉林模考) 在方程mx 2 -my 2 =n 中,若 mn <0,则方程表示的曲线是( ).
A.焦点在x 轴上的椭圆
B.焦点在x 轴上的双曲线
C.焦点在y 轴上的椭圆
D.焦点在y 轴上的双曲线
考点4 双曲线的渐近线
例题
【例1 】(2011·湖南文理·6) 设双曲线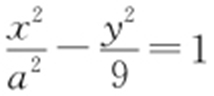 (a >0)的渐近线方程为3x ±2y =0,则a 的值为( ).
(a >0)的渐近线方程为3x ±2y =0,则a 的值为( ).
A.4
B.3
C.2
D.1
条件 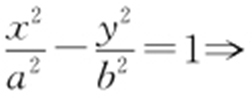 渐近线:
渐近线: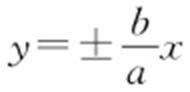 .
.
解析 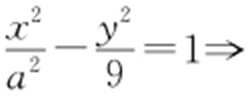 渐近线:
渐近线: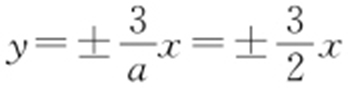 ,即a =2.故选:C.
,即a =2.故选:C.
【例2 】(2012·天津文·11) 已知双曲线C 1 :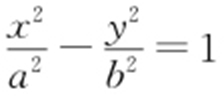 (a >0,b >0)与双曲线C 2 :
(a >0,b >0)与双曲线C 2 :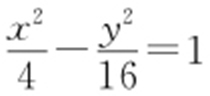 有相同的渐近线,且C 1 的右焦点为
有相同的渐近线,且C 1 的右焦点为 ,则a = ,b = .
,则a = ,b = .
条件  渐近线:
渐近线: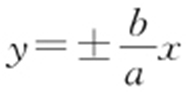 ,且c 2 =a 2 +b 2 .
,且c 2 =a 2 +b 2 .
解析 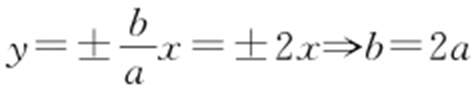 ,又a 2 +b 2 =5,所以a 2 =1,b 2 =4,则a =1,b =2.
,又a 2 +b 2 =5,所以a 2 =1,b 2 =4,则a =1,b =2.
【例3 】(2011·山东理·8) 已知双曲线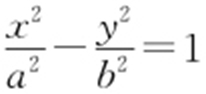 (a >0,b >0)的两条渐近线均和圆C :x 2 +y 2 -6x +5=0相切,且双曲线的右焦点为圆C 的圆心,则该双曲线的方程为( ).
(a >0,b >0)的两条渐近线均和圆C :x 2 +y 2 -6x +5=0相切,且双曲线的右焦点为圆C 的圆心,则该双曲线的方程为( ).
条件 直线与圆相切⇒圆心到直线的距离等于半径r .
解析 渐近线方程: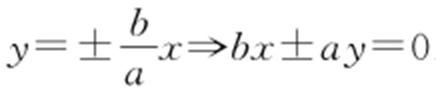 .
.
x 2 +y 2 -6x +5=0⇒(x -3)2 +y 2 =4⇒圆心为(3,0),r =2,
所以有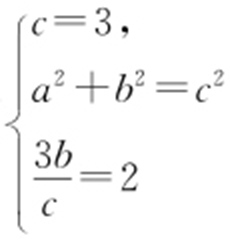 ,
,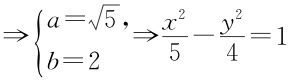 .
.
【例4 】(2013·福建文·4) 双曲线x 2 -y 2 =1的顶点到其渐近线的距离等于( ).
条件 双曲线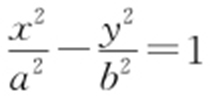 的顶点为(±a ,0),渐近线方程为
的顶点为(±a ,0),渐近线方程为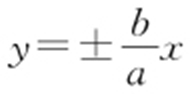 .
.
解析 顶点为(±1,0),渐近线为y =±x ,所以其距离为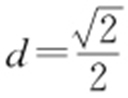 .故选:B.
.故选:B.
总结
(1)渐近线方程为
;
渐近线方程为
.
(2)直线与圆相切⇒圆心到直线的距离为半径.
练习
1.(2012·湖南文理·5) 已知双曲线C :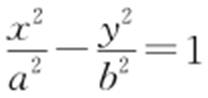 的焦距为10,点P (2,1)在C 的渐近线上,则C 的方程为( ).
的焦距为10,点P (2,1)在C 的渐近线上,则C 的方程为( ).
2.(2014·新课标1理·4) 已知F 是双曲线C :x 2 -my 2 =3m (m >0)的一个焦点,则点F 到C 的一条渐近线的距离为( ).
3.(2013·福建理·3) 双曲线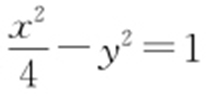 的顶点到其渐近线的距离等于( ).
的顶点到其渐近线的距离等于( ).
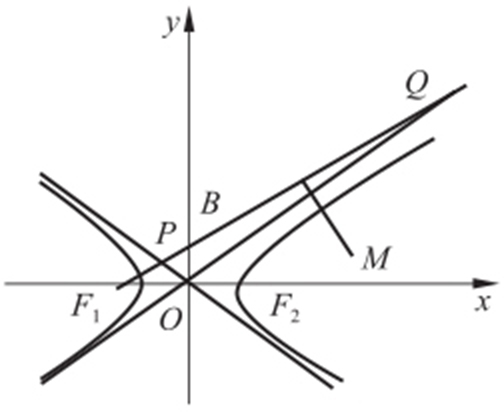
4.(2012·浙江理·8) 如图,F 1 ,F 2 分别是双曲线C :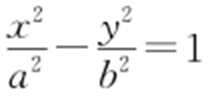 (a ,b >0)的左、右焦点,B 是虚轴的端点,直线F 1 B 与C 的两条渐近线分别交于P ,Q 两点,线段PQ 的垂直平分线与x 轴交于点M .若|MF 2 |=|F 1 F 2 |,则C 的离心率是( ).
(a ,b >0)的左、右焦点,B 是虚轴的端点,直线F 1 B 与C 的两条渐近线分别交于P ,Q 两点,线段PQ 的垂直平分线与x 轴交于点M .若|MF 2 |=|F 1 F 2 |,则C 的离心率是( ).
考点5 焦点三角形与弦心三角形
例题
【例1 】(2012·辽宁文·15) 已知双曲线x 2 -y 2 =1,点F 1 ,F 2 为其两个焦点,点P 为双曲线上一点,若PF 1 ⊥PF 2 ,则|PF 1 |+|PF 2 |的值为 .
条件 ||PF 1 |-|PF 2 ||=2a ,|PF 1 |2 +|PF 2 |2 =|F 1 F 2 |2 .
解析 设|PF 1 |>|PF 2 |,则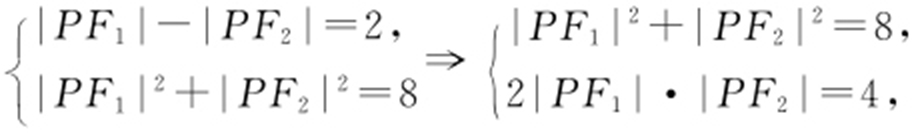 所以
所以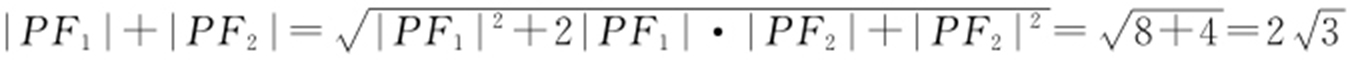 .
.
【例2 】(2013·辽宁文·15) 已知F 为双曲线C :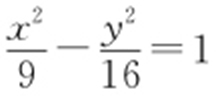 的左焦点,P ,Q 为C 上的点,若PQ 的长等于虚轴长的2倍,点A (5,0)在线段PQ 上,则△PQF 的周长为 .
的左焦点,P ,Q 为C 上的点,若PQ 的长等于虚轴长的2倍,点A (5,0)在线段PQ 上,则△PQF 的周长为 .
条件 判断出A 为右焦点,且利用|PF |-|PA |=|QF |-|QA |=2a .
解析 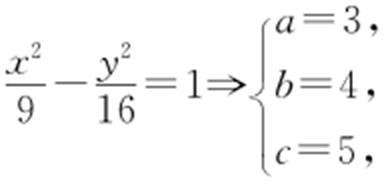 则A 为右焦点,所以|PQ |=4b =16,则|PF |-|PA |=6=|QF |-|QA |,故C △PQF =|PF |+|PA |+|AQ |+|QF |=6+2|PA |+6+2|QA |=12+2|PQ |=12+32=44.
则A 为右焦点,所以|PQ |=4b =16,则|PF |-|PA |=6=|QF |-|QA |,故C △PQF =|PF |+|PA |+|AQ |+|QF |=6+2|PA |+6+2|QA |=12+2|PQ |=12+32=44.
总结
(1)||PF 1 |-|PF 2 ||=2a .
(2)c 2 =a 2 +b 2 .
练习
1.(2013·湖南理·14) 设F 1 ,F 2 是双曲线C :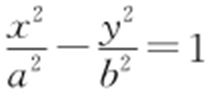 (a >0,b >0)的两个焦点,P 是C 上一点,若|PF 1 |+|PF 2 |=6a ,且△PF 1 F 2 的最小内角为30°,则C 的离心率为 .
(a >0,b >0)的两个焦点,P 是C 上一点,若|PF 1 |+|PF 2 |=6a ,且△PF 1 F 2 的最小内角为30°,则C 的离心率为 .
2.(2003·上海调研) P 是双曲线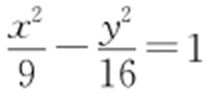 上一点,E ,F 是两焦点,若|PE |·|PF |=32,求∠EPF 的大小.
上一点,E ,F 是两焦点,若|PE |·|PF |=32,求∠EPF 的大小.
考点6 椭圆与双曲线综合
例题

【例1 】(2012·浙江文·8) 如图,中心均为原点O 的双曲线与椭圆有公共焦点,M ,N 是双曲线的两顶点.若M ,O ,N 将椭圆长轴四等份,则双曲线与椭圆的离心率的比值是( ).
条件 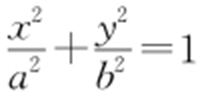 (a >b >0),离心率为
(a >b >0),离心率为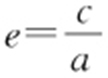 (其中c 2 +b 2 =a 2 );
(其中c 2 +b 2 =a 2 );
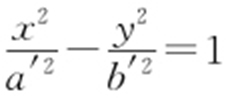 (a′ >0,b′ >0),离心率为
(a′ >0,b′ >0),离心率为 (其中c′ 2 =a′ 2 +b′ 2 ).
(其中c′ 2 =a′ 2 +b′ 2 ).
解析 设椭圆为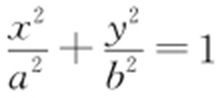 ,双曲线为
,双曲线为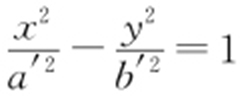 ,有
,有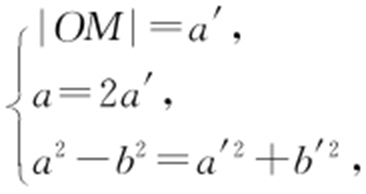 则
则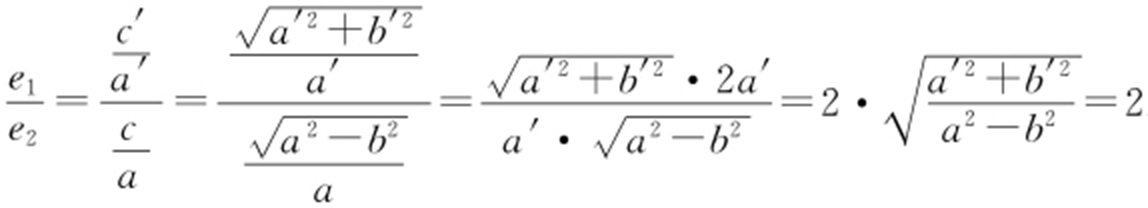 .故选:B.
.故选:B.
【例2 】(2013·浙江文理·9) 如图,F 1 ,F 2 是椭圆C 1 :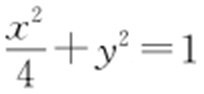 与双曲线C 2 的公共焦点,A ,B 分别是C 1 ,C 2 在第二、四象限的公共点,若四边形AF 1 BF 2 为矩形,则C 2 的离心率是( ).
与双曲线C 2 的公共焦点,A ,B 分别是C 1 ,C 2 在第二、四象限的公共点,若四边形AF 1 BF 2 为矩形,则C 2 的离心率是( ).
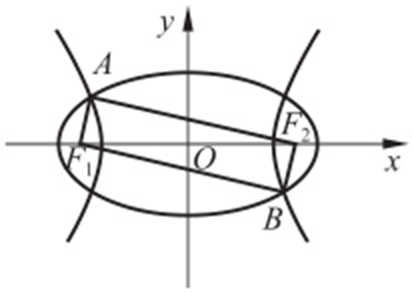
条件 设椭圆的长半轴长为a ,双曲线的实半轴长为a′ ,
解析 设|AF 1 |=x ,|AF 2 |=y ,且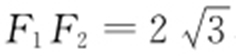 ,则有
,则有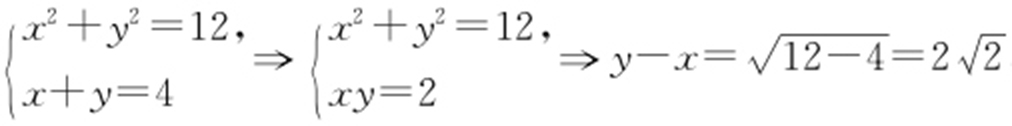 ,所以双曲线的离心率为
,所以双曲线的离心率为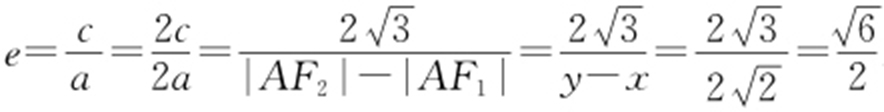 .故选:D.
.故选:D.
总结
(1)动点P 在双曲线中到两焦点距离之差为2a ,在椭圆中其距离之和为2a .
(2)椭圆与双曲线的离心率均为.
练习
1.(2014·山东理·10) 已知a >0,b >0,椭圆C 1 的方程为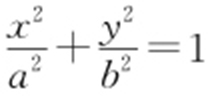 ,双曲线C 2 的方程为
,双曲线C 2 的方程为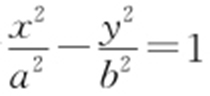 ,C 1 与C 2 的离心率之积为
,C 1 与C 2 的离心率之积为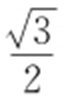 ,则C 2 的渐近线方程为( ).
,则C 2 的渐近线方程为( ).
2.(2014·湖北理·9) 已知F 1 ,F 2 是椭圆和双曲线的公共焦点,P 是它们的一个公共点,且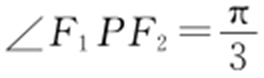 ,则椭圆和双曲线的离心率的倒数之和的最大值为( ).
,则椭圆和双曲线的离心率的倒数之和的最大值为( ).
考点7 椭圆与双曲线离心率专题
例题
【例1 】(2011·辽宁理·13) 已知点(2,3)在双曲线C :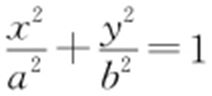 (a >0,b >0)上,C 的焦距为4,则它的离心率为 .
(a >0,b >0)上,C 的焦距为4,则它的离心率为 .
条件 离心率 .
.
解析 (2,3)代入得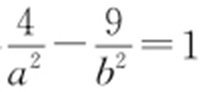 ,又a 2 +b 2 =4,解得a 2 =1,b 2 =3,所以
,又a 2 +b 2 =4,解得a 2 =1,b 2 =3,所以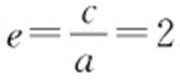 .
.
【例2 】(2011·全国卷1理·7) 设直线L 过双曲线C 的一个焦点,且与C 的一条对称轴垂直,L 与C 交于A ,B 两点,|AB |为C 的实轴长的2倍,则C 的离心率为( ).
条件 双曲线的通径长为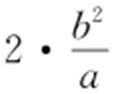 ,离心率
,离心率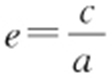 ,其中c 2 =a 2 +b 2 .
,其中c 2 =a 2 +b 2 .
解析 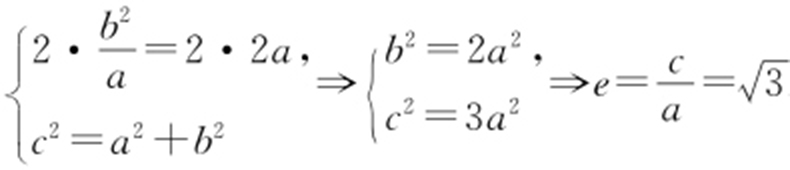 .故选:B.
.故选:B.
【例3 】(2013·湖南文·14) 设F 1 ,F 2 是双曲线C :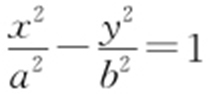 (a >0,b >0)的两个焦点.若在C 上存在一点P ,使PF 1 ⊥PF 2 ,且∠PF 1 F 2 =30°,则C 的离心率为 .
(a >0,b >0)的两个焦点.若在C 上存在一点P ,使PF 1 ⊥PF 2 ,且∠PF 1 F 2 =30°,则C 的离心率为 .
条件 (1)||PF 1 |-|PF 2 ||=2a .
(2)在直角三角形中,30°角所对的边长度是斜边的一半.
解析 设|PF 1 |>|PF 2 |,则有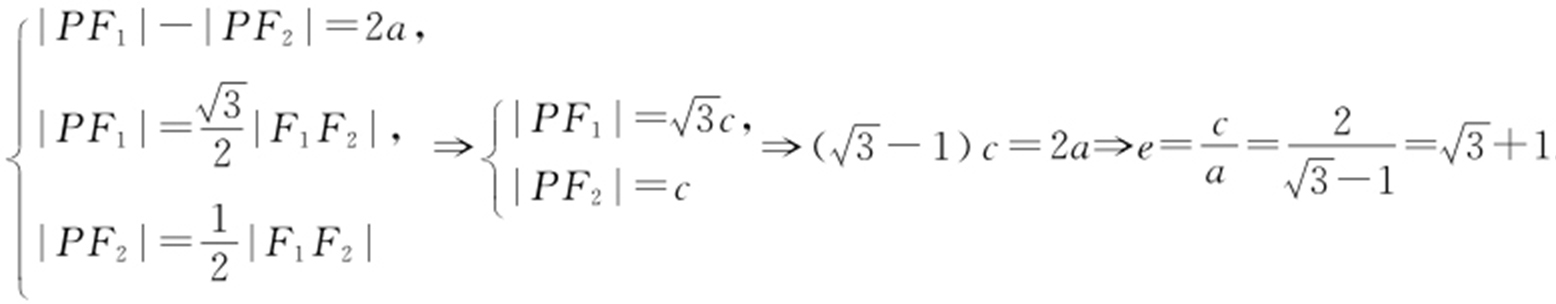 .
.
【例4 】(2011·南昌联考文) 已知F 1 ,F 2 是椭圆的两个焦点,满足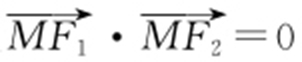 的点M 总在椭圆内部,则椭圆离心率的取值范围是 .
的点M 总在椭圆内部,则椭圆离心率的取值范围是 .
条件 (1)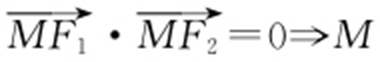 的轨迹为是以|F 1 F 2 |为直径、O 为圆心的圆.
的轨迹为是以|F 1 F 2 |为直径、O 为圆心的圆.
(2)M 在椭圆内部⇒M 轨迹在椭圆内.
解析 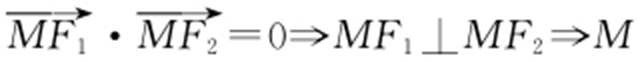 的轨迹为以O 为圆心、|F 1 F 2 |为直径的圆.
的轨迹为以O 为圆心、|F 1 F 2 |为直径的圆.
M :x 2 +y 2 =c 2 ,因为M 在椭圆内部⇒x 2 +y 2 =c 2 在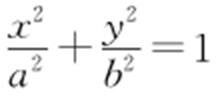 内部,所以
内部,所以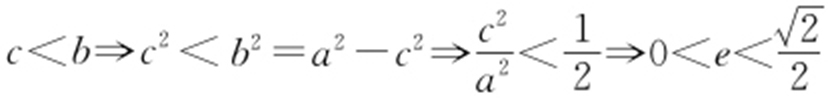 .
.
【例5 】(2011·南昌联考理) 已知F 1 ,F 2 是椭圆的两个焦点,P 是椭圆上一点,且∠F 1 PF 2 =60°,则椭圆离心率e 的取值范围为 .

条件 当P 位于短轴端点时,∠F 1 PF 2 最大.
解析 当P 位于短轴端点时,∠F 1 PF 2 最大.所以∠F 1 PF 2 ≥60°,则∠F 1 PO ≥30°,故得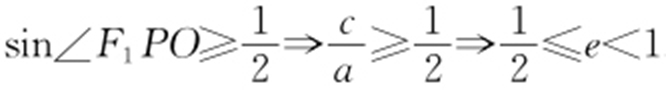 .
.
总结
(1)椭圆、双曲线的通径长为.
(2)当P 位于椭圆的短轴端点时,∠F 1 PF 2 最大.
练习
1.(2012·福建文·5) 已知双曲线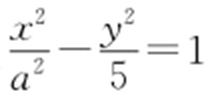 的右焦点为(3,0),则该双曲线的离心率等于( ).
的右焦点为(3,0),则该双曲线的离心率等于( ).
2.(2012·重庆文·14) 设P 为直线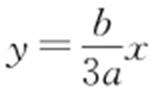 与双曲线
与双曲线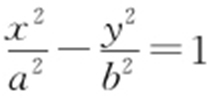 (a >0,b >0)左支的交点,F 1 是左焦点,PF 1 垂直于x 轴,则双曲线的离心率e = .
(a >0,b >0)左支的交点,F 1 是左焦点,PF 1 垂直于x 轴,则双曲线的离心率e = .
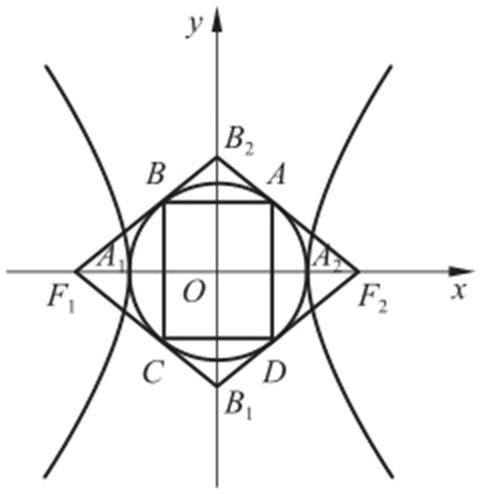
3.(2012·湖北理·14) 如图,双曲线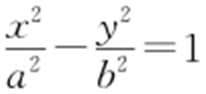 (a ,b >0)的两顶点为A 1 ,A 2 ,虚轴两端点为B 1 ,B 2 ,两焦点为F 1 ,F 2 .若以A 1 A 2 为直径的圆内切于菱形F 1 B 1 F 2 B 2 ,切点分别为A ,B ,C ,D ,则双曲线的离心率e = .
(a ,b >0)的两顶点为A 1 ,A 2 ,虚轴两端点为B 1 ,B 2 ,两焦点为F 1 ,F 2 .若以A 1 A 2 为直径的圆内切于菱形F 1 B 1 F 2 B 2 ,切点分别为A ,B ,C ,D ,则双曲线的离心率e = .
4.(2016·南昌二中模考) 设椭圆 (a >b >0)的两焦点为F 1 ,F 2 ,若椭圆上存在一点Q ,使∠F 1 QF 2 =120°,则椭圆离心率e 的取值范围为 .
(a >b >0)的两焦点为F 1 ,F 2 ,若椭圆上存在一点Q ,使∠F 1 QF 2 =120°,则椭圆离心率e 的取值范围为 .
5.(2013·重庆文·10) 设双曲线C 的中心为点O ,若有且只有一对相交于点O 所成的角为60°的直线A 1 B 1 和A 2 B 2 ,使|A 1 B 1 |=|A 2 B 2 |,其中A 1 ,B 1 和A 2 ,B 2 分别是这对直线与双曲线C 的交点,则该双曲线的离心率的取值范围是( ).
有5个高中生,她们面对学校的新闻采访说了如下的话.爱:“我还没有谈过恋爱.”静香:“爱撒谎了.”玛丽:“我曾经去过昆明.”惠美:“玛丽在撒谎.”千叶子:“玛丽和惠美都在撒谎.”那么,这5个人之中到底有几个人在撒谎呢?
——邵爷(邵菁璟老师)
圆锥曲线是一个只要你能将已知几何条件转化成代数条件,然后算到死就会莫名其妙算出来的神奇考点.
——邵爷(邵菁璟老师)
人才和天才只差一个“二”,故,人才很精,而天才总是有点二.
——村长(付文伟老师)
傻子偷乞丐的钱包,被瞎子看到了,哑巴大吼一声,把聋子吓了一跳,驼子挺身而出,瘸子飞起一脚,通缉犯要拉他去公共安全专家局,麻子说,看我的面子算了.
——村长(付文伟老师)
理想就像贴身衣物,要有,但不能逢人就去证明你有!
——村长(付文伟老师)
我向星星许了个愿,我并不是真的相信它,但是反正也是免费的,而且也没有证据证明它不灵.
——村长(付文伟老师)
中国式父母:
5岁:孩子,我给你报了少年宫.7岁:孩子,我给你报了奥数班.15岁:孩子,我给你报了重点中学.18岁:孩子,我给你报了高考突击班.23岁:孩子,我给你报了公务员.32岁:孩子,我给你报了《非诚勿扰》.
——村长(付文伟老师)
上联:学生证准考证身份证证证没带;
下联:听力题阅读题作文题题题不做.
横批:谢谢参与.
——村长(付文伟老师)
父亲问我人生有什么追求?
我回答金钱和美女,父亲凶狠地打了我的脸;我回答事业与爱情,父亲赞赏地摸了我的头.
——村长(付文伟老师)
每天叫醒我们的不应该是闹钟,而应该是梦想.可是我的梦想就是:每天睡觉睡到自然醒!
——村长(付文伟老师)
世界上最遥远的距离,不是生与死,而是马上考试了,别人在复习,自己却在预习.更悲剧的是,人家预习的都过了,你复习了却没过.
——村长(付文伟老师)
一个人知道自己为什么而活,就可以忍受任何一种生活.
——尼采
人的一切痛苦,本质上都是对自己的愤怒.
——王小波
建高楼大厦,地基才是基础,砖头只是材料.
——娴姐(刘娴老师)
学数学两大标配:纸和笔.不管平常还是考试,请手中有笔有纸.如果是光着膀子上数学课,那就是耍流氓!
——娴姐(刘娴老师)
课堂上数学老师讲练习,他问我们:“接下来要讲哪一道题啦?”我们齐声喊:“第八题(较难的).”他清了清嗓子,回道:“好,那么接下来我们来讲一下第十题(最简单的).”这样的老师你们遇到了吗?
——娴姐(刘娴老师)



















