第8章　解析几何2015年真题必刷

直线与圆

1．（2015·安徽文·8）　直线3x +4y =b 与圆x ² +y ² -2x -2y +1=0相切，则b =（　　）．

A．-2或12
B．2或-12
C．-2或-12
D．2或12

2．（2015·北京文·2）　圆心为（1，1）且过原点的圆的方程是（　　）．

A．(x -1)² +(y -1)² =1
B．(x +1)² +(y +1)² =1
C．(x +1)² +(y +1)² =2
D．(x -1)² +(y -1)² =2

3．（2015·广东理·5）　平行于直线2x +y +1=0且与圆x ² +y ² =5相切的直线的方程是（　　）．

4．（2015·广东文·20，理·21）　已知过原点的动直线l 与圆C ₁ ：x ² +y ² -6x +5=0相交于不同的两点A ，B ．

（1）求圆C ₁ 的圆心坐标；

（2）求线段AB 的中点M 的轨迹C 的方程；

（3）是否存在实数k ，使得直线L ：y =k (x -4)与曲线C 只有一个交点：若存在k ，求出其取值范围；若不存在，说明理由．

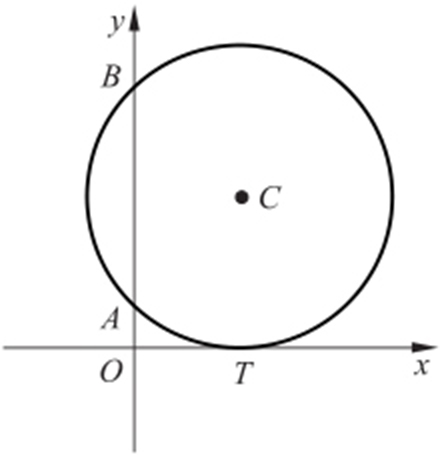
5．（2015·湖北文·16）　如图，已知圆C 与x 轴相切于点T (1，0)，与y 轴正半轴交于两点A ，B （B 在A 的上方），且|AB |=2．

（1）圆C 的标准方程为 ；

（2）圆C 在点B 处的切线在x 轴上的截距为 ．

6．（2015·湖南文·13）　若直线3x -4y +5=0与圆x ² +y ² =r ² （r ＞0）相交于两点A ，B ，且∠AOB =120°（O 为坐标原点），则r = ．

7．（2015·山东理·9）　一条光线从点（-2，-3）射出，经y 轴反射与圆(x +3)² +(y -2)² =1相切，则反射光线所在的直线的斜率为（　　）．

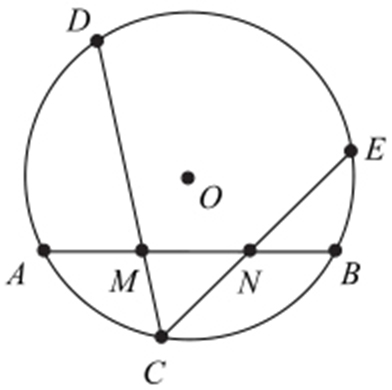
8．（2015·天津文·6，理·5）　如图，在圆O 中，M ，N 是弦AB 的三等份点，弦CD ，CE 分别经过点M ，N ．若CM =2，MD =4，CN =3，则线段NE 的长为（　　）．

9．（2015·新课标1理·14）　一个圆经过椭圆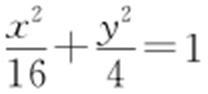 的三个顶点，且圆心在x 轴的正半轴上，则该圆的标准方程为 ．

10．（2015·新课标1文·20）　已知过点A (0，1)且斜率为k 的直线l 与圆C ：(x -2)² +(y -3)² =1交于M ，N 两点．

（1）求k 的取值范围；

（2）若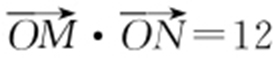 ，其中O 为坐标原点，求|MN |．

11．（2015·新课标2理·7）　过三点A (1，3)，B (4，2)，C (1，-7)的圆交y 轴于M ，N 两点，则|MN |=（　　）．

12．（2015·新课标2文·7）　已知三点A (1，0)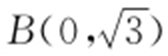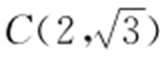， ， ，则△ABC 外接圆的圆心到原点的距离为（　　）．

13．（2015·重庆理·8）　已知直线l ：x +ay -1=0（a ∈R ）是圆C ：x ² +y ² -4x -2y +1=0的对称轴，过点A (-4，a )作圆C 的一条切线，切点为B ，则|AB |=（　　）．

A．2
B．
C．6
D．

圆锥曲线

14．（2015·广东文·8）　已知椭圆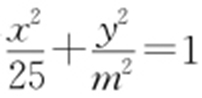 （m ＞0）的左焦点为F ₁ (-4，0)，则m =（　　）．

A．9
B．4
C．3
D．2

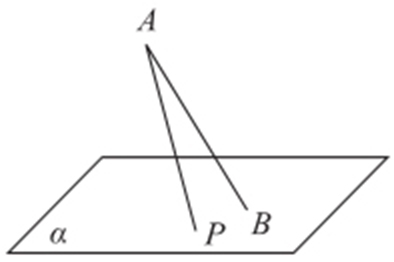
15．（2015·浙江文·7）　如图，斜线段AB 与平面α 所成的角为60°，B 为斜足，平面α 上的动点P 满足∠PAB =30°，则点P 的轨迹是（　　）．

A．直线
B．抛物线
C．椭圆
D．双曲线的一支

16．（2015·浙江文·15）　椭圆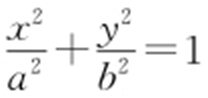 （a ＞b ＞0）的右焦点F (c ，0)关于直线 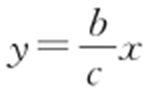的对称点Q 在椭圆上，则椭圆的离心率是 ．

17．（2015·重庆理·21）　如图，椭圆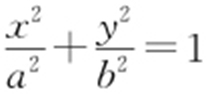 （a ＞b ＞0）的左、右焦点分别为F ₁ ，F ₂ ，过F ₂ 的直线交椭圆于P ，Q 两点，且PQ ⊥PF ₁ ．

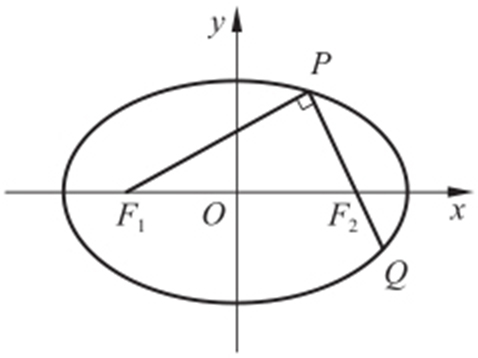
（1）若 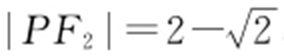， ，求椭圆的标准方程；

（2）若|PF ₁ |=|PQ |，求椭圆的离心率e ．

18．（2015·福建理·3）　若双曲线E 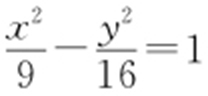： 的左、右焦点分别为F ₁ ，F ₂ ，点P 在双曲线E 上，且|PF ₁ |=3，则|PF ₂ |=（　　）．

A．11
B．9
C．5
D．3

19．（2015·安徽理·4）　下列双曲线中，焦点在y 轴上且渐近线方程为y =±2x 的是（　　）．

20．（2015·安徽文·6）　下列双曲线中，渐近线方程为y =±2x 的是（　　）．

21．（2015·北京理·10）　已知双曲线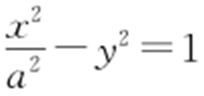 （a ＞0）的一条渐近线为 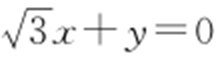，则a = ．

22．（2015·北京文·12）　已知（2，0）是双曲线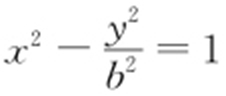 （b ＞0）的一个焦点，则b = ．

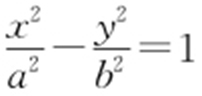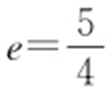23．（2015·广东理·7）　已知双曲线C ： 的离心率 ，且其右焦点F ₂ (5，0)，则双曲线C 的方程为（　　）．

24．（2015·浙江理·9）　双曲线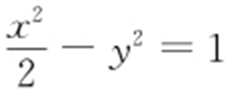 的焦距是 ，渐近线方程是 ．

25．（2015·四川文·7，理·5）　过双曲线 的右焦点且与x 轴垂直的直线，交该双曲线的两条渐近线于A ，B 两点，则|AB |=（　　）．

26．（2015·新课标2文·15）　已知双曲线过点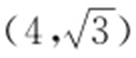 ，且渐近线方程为 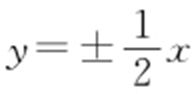，则该双曲线的标准方程为 ．

27．（2015·天津理·6）　已知双曲线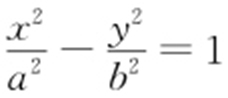 （a ＞0，b ＞0）的一条渐近线过点 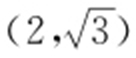，且双曲线的一个焦点在抛物线 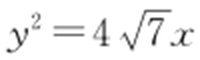的准线上，则双曲线的方程为（　　）．

28．（2015·天津文·5）　已知双曲线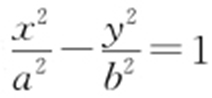 （a ＞0，b ＞0）的一个焦点为F (2，0)，且双曲线的渐近线与圆(x -2)² +y ² =3相切，则双曲线的方程为（　　）．

29．（2015·新课标1文·16）　已知F 是双曲线C 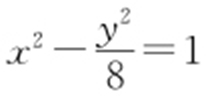： 的右焦点，P 是C 的左支上一点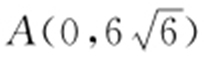， ．当△APF 周长最小时，该三角形的面积为 ．

30．（2015·重庆理·10）　设双曲线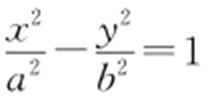 （a ＞0，b ＞0）的右焦点为F ，右定点为A ，过F 作AF 的垂线与双曲线交于B ，C 两点，过B ，C 分别作AC ，AB 的垂线，两垂线交于点D ，若D 到直线BC 的距离小于 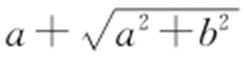，则该双曲线的渐近线斜率的取值范围是（　　）．

31．（2015·陕西理·14）　若抛物线y ² =2px （p ＞0）的准线经过双曲线x ² -y ² =1的一个焦点，则p = ．

32．（2015·陕西文·3）　已知抛物线y ² =2px （p ＞0）的准线经过点（-1，1），则抛物线焦点坐标为（　　）．

A．（-1，0）
B．（1，0）
C．（0，-1）
D．（0，1）

33．（2015·四川文·10，理·10）　设直线l 与抛物线y ² =4x 相交于A ，B 两点，与圆(x -5)² +y ² =r ² （r ＞0）相切于点M ，且M 为线段AB 的中点．若这样的直线l 恰有4条，则r 的取值范围是（　　）．

A．（1，3）
B．（1，4）
C．（2，3）
D．（2，4）

34．（2015·新课标1文·5）　已知椭圆E 的中心在坐标原点，离心率为 ，E 的右焦点与抛物线C ：y ² =8x 的焦点重合，A ，B 是C 的准线与E 的两个交点，则|AB |=（　　）．

A．3
B．6
C．9
D．12

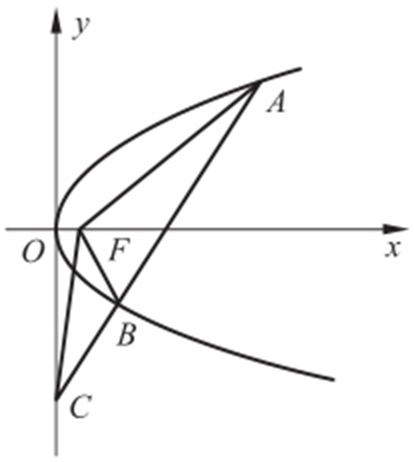
35．（2015·浙江理·5）　如图，设抛物线y ² =4x 的焦点为F ，不经过焦点的直线上有三个不同的点A ，B ，C ，其中点A ，B 在抛物线上，点C 在y 轴上，则△BCF 与△ACF 的面积之比是（　　）．

36．（2015·福建文·11）　已知椭圆E 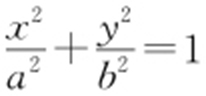： （a ＞b ＞0）的右焦点为F ．短轴的一个端点为M ，直线l ：3x -4y =0交椭圆E 于A ，B 两点．若|AF |+|BF |=4，点M 到直线l 的距离不小于 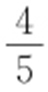，则椭圆E 的离心率的取值范围是（　　）．

37．（2015·湖北文·9，理·8）　将离心率为e ₁ 的双曲线C ₁ 的实半轴长a 和虚半轴长b （a ≠b ）同时增加m （m ＞0）个单位长度，得到离心率为e ₂ 的双曲线C ₂ ，则（　　）．

A．对任意的a ，b ，e ₁ ＞e ₂
B．当a ＞b 时，e ₁ ＞e ₂ ；当a ＜b 时，e ₁ ＜e ₂
C．对任意的a ，b ，e ₁ ＜e ₂
D．当a ＞b 时，e ₁ ＜e ₂ ；当a ＜b 时，e ₁ ＞e ₂

38．（2015·湖南理·13）　设F 是双曲线C 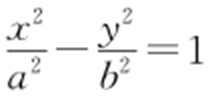： 的一个焦点，若C 上存在点P ，使线段PF 的中点恰为其虚轴的一个端点，则C 的离心率为 ．

39．（2015·湖南文·6）　若双曲线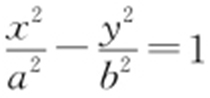 的一条渐近线经过点（3，-4），则此双曲线的离心率为（　　）．

40．（2015·山东理·15）　平面直角坐标系xOy 中，双曲线C ₁ 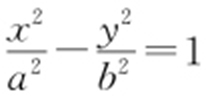： （a ＞0，b ＞0）的渐近线与抛物线C ₂ ：x ² =2py （p ＞0）交于点O ，A ，B ，若△OAB 的垂心为C ₂ 的焦点，则C ₁ 的离心率为 ．

41．（2015·山东文·15）　过双曲线C 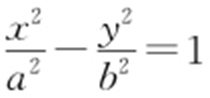： （a ＞0，b ＞0）的右焦点作一条与其渐近线平行的直线，交C 于点P ．若点P 的横坐标为2a ，则C 的离心率为 ．

42．（2015·新课标1理·5）　已知M (x ₀ ，y ₀ )是双曲线C 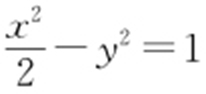： 上的一点，F ₁ ，F ₂ 是双曲线C 的两个焦点，若 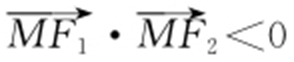，则y ₀ 的取值范围是（　　）．

43．（2015·新课标2理·11）　已知A ，B 为双曲线E 的左、右顶点，点M 在E 上，△ABM 为等腰三角形，且顶角为120°，则E 的离心率为（　　）．

44．（2015·新课标2理·20）　已知椭圆C ：9x ² +y ² =m ² （m ＞0），直线l 不过原点O 且不平行于坐标轴，l 与C 有两个交点A ，B ，线段AB 的中点为M ．

（1）证明：直线OM 的斜率与l 的斜率的乘积为定值；

（2）若l 过点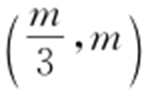 ，延长线段OM 与C 交于点P ，四边形OAPB 能否为平行四边形？若能，求此时l 的斜率；若不能，说明理由．

45．（2015·浙江文·19）　如图，已知抛物线C ₁ 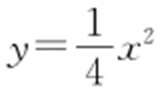： ，圆C ₂ ：x ² +(y -1)² =1，过点P (t ，0)（t ＞0）作不过原点O 的直线PA ，PB 分别与抛物线C ₁ 和圆C ₂ 相切，A ，B 为切点．

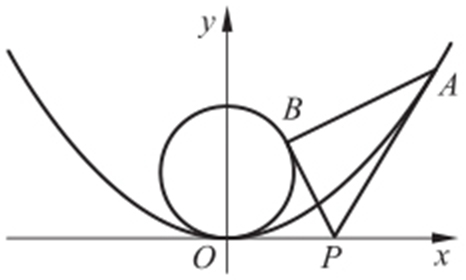
（1）求点A ，B 的坐标；

（2）求△PAB 的面积．

注：直线与抛物线有且只有一个公共点，且与抛物线的对称轴不平行，则该直线与抛物线相切，称该公共点为切点．

46．（2015·浙江理·19）　已知椭圆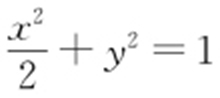 上两个不同的点A ，B 关于直线 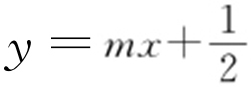对称．

（1）求实数m 的取值范围；

（2）求△AOB 面积的最大值（O 为坐标原点）．

47．（2015·北京理·19）　已知椭圆C 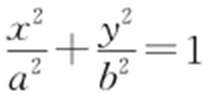： （a ＞b ＞0）的离心率为 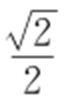，点P (0，1)和点A (m ，n )（m ≠0）都在椭圆C 上，直线PA 交x 轴于点M ．

（1）求椭圆C 的方程，并求点M 的坐标（用m ，n 表示）；

（2）设O 为原点，点B 与点A 关于x 轴对称，直线PB 交x 轴于点N ．问：y 轴上是否存在点Q ，使得∠OQM =∠ONQ ？若存在，求点Q 的坐标；若不存在，说明理由．

48．（2015·北京文·20）　已知椭圆C ：x ² +3y ² =3，过点D (1，0)且不过点E (2，1)的直线与椭圆C 交于A ，B 两点，直线AE 与直线x =3交于点M ．

（1）求椭圆C 的离心率；

（2）若AB 垂直于x 轴，求直线BM 的斜率；

（3）试判断直线BM 与直线DE 的位置关系，并说明理由．

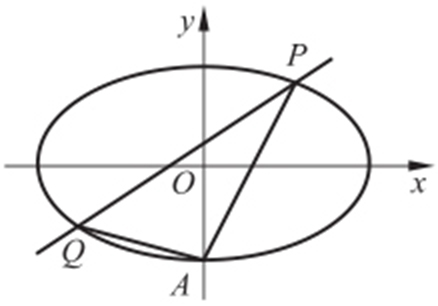
49．（2015·陕西文·20）　如图，椭圆E 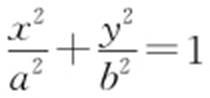： （a ＞b ＞0）经过点A (0，-1)，且离心率为 ．

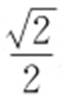（1）求椭圆E 的方程；

（2）经过点（1，1），且斜率为k 的直线与椭圆E 交于不同两点P ，Q （均异于点A ），证明：直线AP 与AQ 的斜率之和为2．

50．（2015·天津文·19）　已知椭圆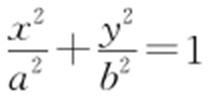 （a ＞b ＞0）的上顶点为B ，左焦点为F ，离心率为 ．

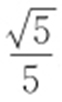（1）求直线BF 的斜率；

（2）设直线BF 与椭圆交于点P （P 异于点B ），过点B 且垂直于BF 的直线与椭圆交于点Q （Q 异于点B ），直线PQ 与x 轴交于点M ，|PM |=l |MQ |．

①求l 的值；

②若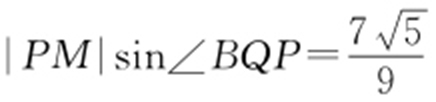 ，求椭圆的方程．

51．（2015·新课标1理·20）　在平面直角坐标系xOy 中，曲线C ： 与直线l ：y =kx +a （a ＞0）交于M ，N 两点．

（1）当k =0时，分别求C 在M 点和N 点处的切线方程；

（2）y 轴上是否存在点P ，使得当k 变动时，总有∠OPM =∠OPN ？说明理由．

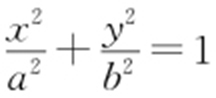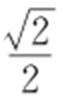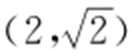52．（2015·新课标2文·20）　已知椭圆C ： （a ＞b ＞0）的离心率为 ，点 在C 上．

（1）求C 的方程；

（2）直线l 不经过原点O ，且不平行于坐标轴，l 与C 有两个交点A ，B ，线段AB 中点为M ，证明：直线OM 的斜率与直线l 的斜率乘积为定值．

53．（2015·福建理·18）　已知椭圆E 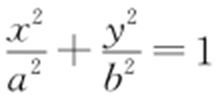： （a ＞b ＞0）过点 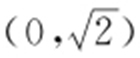，且离心率为 ．

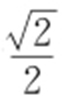（1）求椭圆E 的方程；

（2）设直线x =my -1（m ∈R ）交椭圆E 于A ，B 两点，判断点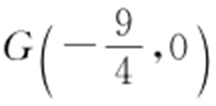 与以线段AB 为直径的圆的位置关系，并说明理由．

54．（2015·湖南理·20）　已知抛物线C ₁ ：x ² =4y 的焦点F 也是椭圆C ₂ 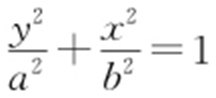： （a ＞b ＞0）的一个焦点，C ₁ 与C ₂ 的公共弦长为 ．

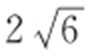（1）求C ₂ 的方程；

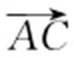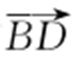（2）过点F 的直线l 与C ₁ 相交于A ，B 两点，与C ₂ 相交于C ，D 两点，且 与 同向．

①若|AC |=|BD |，求直线l 的斜率；

②设C ₁ 在点A 处的切线与x 轴的交点为M ，证明：直线l 绕点F 旋转时，△MFD 总是钝角三角形．

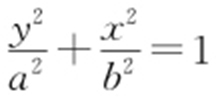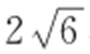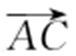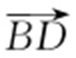55．（2015·湖南文·20）　已知抛物线C ₁ ：x ² =4y 的焦点F 也是椭圆C ₂ ： （a ＞b ＞0）的一个焦点，C ₁ 与C ₂ 的公共弦长为 ，过点F 的直线l 与C ₁ 相交于A ，B 两点，与C ₂ 相交于C ，D 两点，且 与 同向．

（1）求C ₂ 的方程；

（2）若|AC |=|BD |，求直线l 的斜率．

极坐标与参数方程

56．（2015·安徽理·12）　在极坐标系中，圆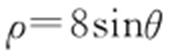 上的点到直线 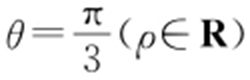距离的最大值是 ．

57．（2015·北京理·11）　在极坐标系中，点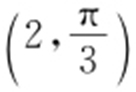 到直线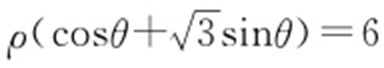 的距离为 ．

58．（2015·湖南文·12）　在直角坐标系xOy 中，以坐标原点为极点、x 轴正半轴为极轴建立极坐标系．若曲线C 的极坐标方程为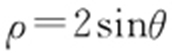 ，则曲线C 的直角坐标方程为 ．

59．（2015·福建理·21）　在平面直角坐标系xOy 中，圆C 的参数方程为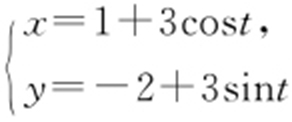 （t 为参数）．在极坐标系（与平面直角坐标系xOy 取相同的长度单位，且以原点O 为极点、以x 轴非负半轴为极轴）中，直线l 的方程为 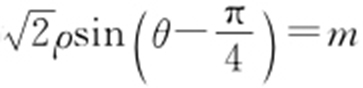，m ∈R ．

（1）求圆C 的普通方程及直线l 的直角坐标方程；

（2）设圆心C 到直线l 的距离等于2，求m 的值．

60．（2015·广东理·14）　已知直线l 的极坐标方程为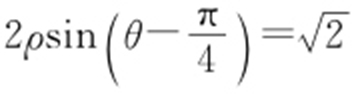 ，点A 的极坐标为 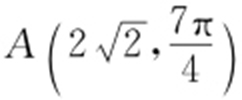，则点A 到直线l 的距离为 ．

61．（2015·湖南理·16）　已知直线l 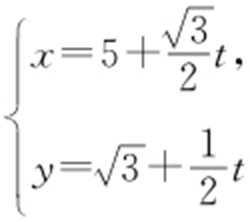： （t 为参数），以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为 ．

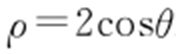（1）将曲线C 的极坐标方程化为直角坐标方程；

（2）设点M 的直角坐标为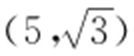 ，直线l 与曲线C 的交点为A ，B ，求|MA |·|MB |的值．

62．（2015·重庆理·15）　已知直线l 的参数方程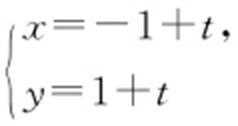 （t 为参数），以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为 ，则直线l 与曲线C 的交点的极坐标为 ．

63．（2015·陕西文理·23）　在直角坐标系xOy 中，直线l 的参数方程为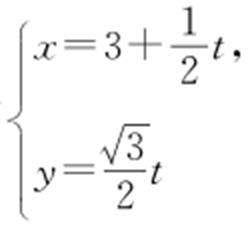 （t 为参数）．以原点为极点，x 轴正半轴为极轴建立极坐标系，⊙C 的极坐标方程为 ．

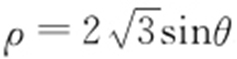（1）写出⊙C 的直角坐标方程；

（2）P 为直线l 上一动点，当P 到圆心C 的距离最小时，求P 的直角坐标．

64．（2015·新课标1文理·23）　在直角坐标系xOy 中，直线C ₁ ：x =-2，圆C ₂ ：(x -1)² +(y -2)² =1，以坐标原点为极点、x 轴的正半轴为极轴建立极坐标系．

（1）求C ₁ ，C ₂ 的极坐标方程；

（2）若直线C ₃ 的极坐标方程为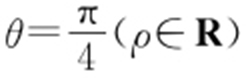 ，设C ₂ 与C ₃ 的交点为M ，N ，求△C ₂ MN 的面积．

65．（2015·新课标2文理·23）　在直角坐标系xOy 中，曲线C ₁ 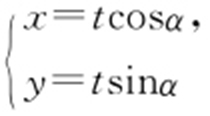： （t 为参数，t ≠0），其中0≤α ＜π，在以O 为极点、x 轴正半轴为极轴的极坐标系中，曲线C ₂ 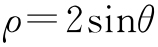： ，C ₃ ： ．

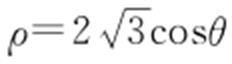（1）求C ₂ 与C ₃ 交点的直角坐标；

（2）若C ₁ 与C ₂ 相交于点A ，C ₁ 与C ₃ 相交于点B ，求|AB |的最大值．

66．（2015·广东文·14）　在平面直角坐标系xOy 中，以原点O 为极点、x 轴的正半轴为极轴建立极坐标系．曲线C ₁ 的极坐标方程为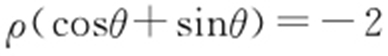 ，曲线C ₂ 的参数方程为 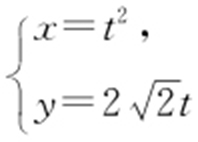（t 为参数），则C ₁ 与C ₂ 交点的直角坐标为 ．

67．（2015·湖北理·16）　在直角坐标系xOy 中，以O 为极点、x 轴的正半轴为极轴建立极坐标系．已知直线l 的极坐标方程为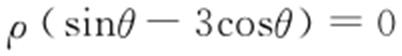 ，曲线C 的参数方程为 （t 为参数），l 与C 相交于A ，B 两点，则|AB |= ．