第2章 圆
1.圆的标准方程:以点C (a ,b )为圆心,r 为半径的圆的标准方程是(x -a )2 +(y -b )2 =r 2 .
2.圆的一般方程:(1) x 2 +y 2 +Dx +Ey +F =0 ( D 2 +E 2 -4F >0 ),其中圆心为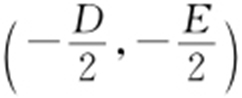 ,半径
,半径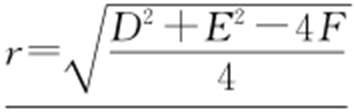 .
.
(2) Ax 2 +By 2 +Cxy +Dx +Ey +F =0 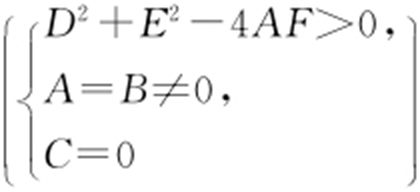 其中圆心为
其中圆心为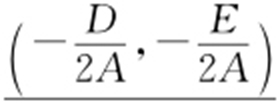 ,半径
,半径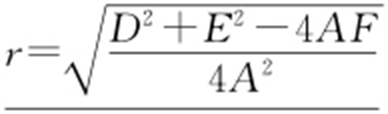 .
.
3.圆的变形方程.
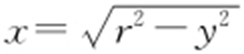 ,表示圆的右半部分;
,表示圆的右半部分;
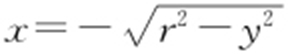 ,表示圆的左半部分;
,表示圆的左半部分;
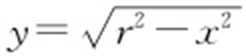 ,表示圆的上半部分;
,表示圆的上半部分;
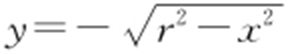 ,表示圆的下半部分.
,表示圆的下半部分.
4.若两圆O 1 :x 2 +y 2 +D 1 x +E 1 y +F 1 =0,O 2 :x 2 +y 2 +D 2 x +E 2 y +F 2 =0相交,则公共弦方程为(D 1 -D 2 )x +(E 1 -E 2 )y +F 1 -F 2 =0 .
5.直线Ax +By +C =0与圆(x -a )2 +(y -b )2 =R 2 相交的弦长公式为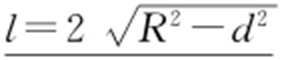 ,其中d 表示圆心到直线的距离,
,其中d 表示圆心到直线的距离, 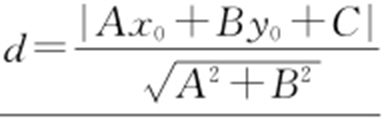 .
.
6.过圆x 2 +y 2 +Dx +Ey +F =0外一点P (x 0 ,y 0 )的切线长公式: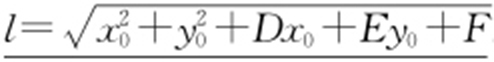 .
.
7.过圆x 2 +y 2 +Dx +Ey +F =0上一点P (x 0 ,y 0 )的切线方程: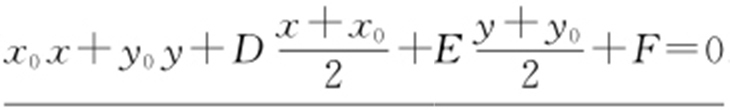 .
.
8.圆系方程.
过圆O 1 :x 2 +y 2 +D 1 x +E 1 y +F 1 =0,O 2 :x 2 +y 2 +D 2 x +E 2 y +F 2 =0的交点的圆系方程为 x 2 +y 2 +D 1 x +E 1 y +F 1 +λ (x 2 +y 2 +D 2 x +E 2 y +F 2 )=0 ,其中λ ≠-1 ,但此圆系不含圆 O 2 .
9.位置关系(位置关系与数学方程的转换).
(1)点P (x 0 ,y 0 )与圆(x -a )2 +(y -b )2 =R 2 的位置关系:
当(x 0 -a )2 +(y 0 -b )2 <R 2 时,点在圆内 ;
当(x 0 -a )2 +(y 0 -b )2 =R 2 时,点在圆上 ;
当(x 0 -a )2 +(y 0 -b )2 >R 2 时,点在圆外 .
(2)直线Ax +By +C =0与圆(x -a )2 +(y -b )2 =R 2 的位置关系:
①相离.
d >R ,其中d 是圆心到直线的距离 .
②相切.
d =R ,其中d 是圆心到直线的距离 .
③相交.
d <R ,其中d 是圆心到直线的距离 .
(3)圆与圆的位置关系(O 1 :x 2 +y 2 +D 1 x +E 1 y +F 1 =0,O 2 :x 2 +y 2 +D 2 x +E 2 y +F 2 =0):
①外离:|O 1 O 2 |>R 1 +R 2 .
②外切:|O 1 O 2 |=R 1 +R 2 .
③相交:|R 1 -R 2 |<|O 1 O 2 |<R 1 +R 2 .
④内切:|O 1 O 2 |=|R 1 -R 2 | .
⑤内含:0≤|O 1 O 2 |<|R 1 -R 2 | .
考点1 圆的方程
例题
【例1 】(2016·浙江文·10) 已知a ∈R ,方程a 2 x 2 +(a +2)y 2 +4x +8y +5a =0表示圆,则圆心坐标是 ,半径是 .
条件 “方程Ax 2 +By 2 +Cxy +Dx +Ey +F =0代表圆”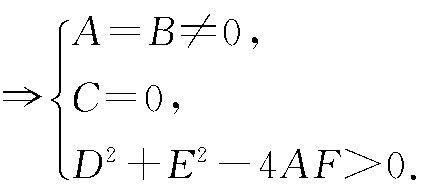
圆心点的坐标
解析 因为该方程代表圆,所以a 2 =a +2,解得a =2或a =-1.
当a =2时,方程为 ,不满足D 2 +E 2 -4F >0,舍去.
,不满足D 2 +E 2 -4F >0,舍去.
当a =-1时,方程为x 2 +y 2 +4x +8y -5=0,此时D 2 +E 2 -4F =100>0,满足条件.
所以圆方程为x 2 +y 2 +4x +8y -5=0,化成标准方程知,(x +2)2 +(y +4)2 =25.
所以圆心为(-2,-4),R =5.
【例2 】(2015·北京文·2) 圆心为(1,1)且过原点的圆的方程是( ).
A.(x -1)2 +(y -1)2 =1
B.(x +1)2 +(y +1)2 =1
C.(x +1)2 +(y +1)2 =2
D.(x -1)2 +(y -1)2 =2
条件 以(a ,b )为圆心、半径为r 的圆⇒(x -a )2 +(y -b )2 =r 2 .
解析 因为圆心为(1,1)且过原点,所以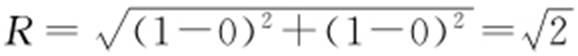 ,因此方程为(x -1)2 +(y -1)2 =2.故选:D.
,因此方程为(x -1)2 +(y -1)2 =2.故选:D.
【例3 】(2015·新课标2文·7) 已知三点A (1,0), ,
, ,则△ABC 外接圆的圆心到原点的距离为( ).
,则△ABC 外接圆的圆心到原点的距离为( ).
条件 等边三角形的四心合一.
重心坐标公式:△ABC 的三点坐标分别是A (xA ,yA ),B (xB ,yB ),C (xC ,yC ),则△ABC 的重心坐标为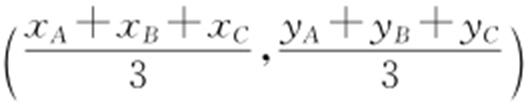 .
.
解析 因为A (1,0),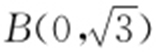 ,
,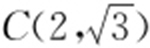 ,所以AB =2,AC =2,BC =2,因此△ABC 为等边三角形,所以△ABC 外接圆的圆心为
,所以AB =2,AC =2,BC =2,因此△ABC 为等边三角形,所以△ABC 外接圆的圆心为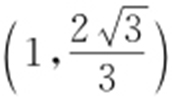 ,因此
,因此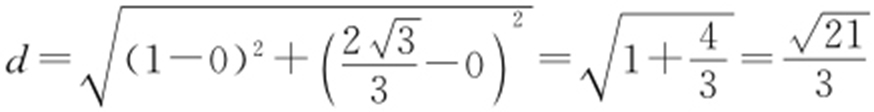 ,故选:B.
,故选:B.
总结
(1)二元二次方程代表圆,其中系数满足条件.
(2)圆心为(x 0 ,y 0 )、半径为R 的圆方程为(x -x 0 )2 +(y -y 0 )2 =R 2 .
(3)涉及四心问题时,切记关注三角形的形状.
练习
1.(2012·辽宁文·7) 将圆x 2 +y 2 -2x -4y +1=0平分的直线是( ).
A.x +y -1=0
B.x +y +3=0
C.x -y +1=0
D.x -y +3=0
2.(2014·陕西理·11) 若圆C 的半径为1,其圆心与点(1,0)关于直线y =x 对称,则圆C 的标准方程为 .
3.(2016·天津文·12) 已知圆C 的圆心在x 轴的正半轴上,点 在圆C 上,且圆心到直线2x -y =0的距离为
在圆C 上,且圆心到直线2x -y =0的距离为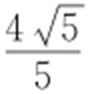 ,则圆C 的方程为 .
,则圆C 的方程为 .
考点2 直线与圆的位置关系
例题
【例1 】(2013·陕西文·8) 已知点M (a ,b )在圆O :x 2 +y 2 =1外,则直线ax +by =1与圆O 的位置关系是( )
A.相切
B.相交
C.相离
D.不确定
条件 (1)某点(x 0 ,y 0 )在圆(x -x 1 )2 +(y -y 1 )2 =R 2 外⇒(x 0 -x 1 )2 +(y 0 -y 1 )2 >R 2 .
(2)确定直线与圆的关系(找圆心到直线距离与半径):
①d >R ⇒相离;
②d =R ⇒相切;
③d <R ⇒相交.
解析 因为点M (a ,b )在圆O :x 2 +y 2 =1外,所以a 2 +b 2 >1,又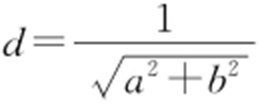 ,R =1,同时有a 2 +b 2 >1,所以
,R =1,同时有a 2 +b 2 >1,所以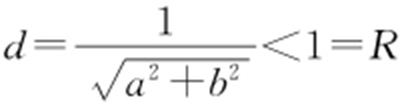 ,因此圆O 与直线的位置关系为相交.故选:B.
,因此圆O 与直线的位置关系为相交.故选:B.
【例2 】(2015·广东理·21,文·20) 已知过原点的动直线l 与圆C 1 :x 2 +y 2 -6x +5=0相交于不同的两点A ,B .
(1)求圆C 1 的圆心坐标;
(2)求线段AB 的中点M 的轨迹C 的方程;
(3)是否存在实数k ,使得直线L :y =k (x -4)与曲线c 只有一个交点.若存在k ,求出其取值范围;若不存在,说明理由.
条件 (1)中点坐标公式:设A (xA ,yA ),B (xB ,yB ),则AB 中点为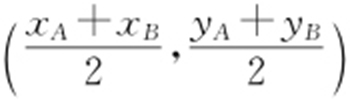 .
.
(2)直线与曲线c 只有一个交点⇒切线.
解析 (1)将圆C 1 化成标准式,得(x -3)2 +y 2 =4,所以圆心为(3,0).
(2)设直线lAB :y =kx ,设A (x 1 ,y 1 ),B (x 2 ,y 2 ),M (x ,y ),联立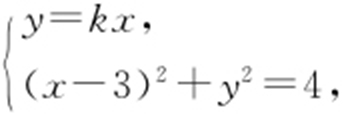 得:(1+k 2 )x 2 -6x +5=0.
得:(1+k 2 )x 2 -6x +5=0.
所以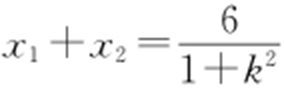 ,
,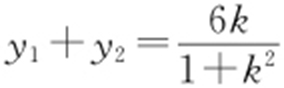 ,因此知
,因此知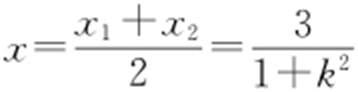 ,
,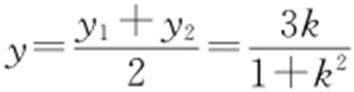 .
.
消去k ,知x 2 +y 2 -3x =0,又因为是相交于两点,所以Δ >0,即36-4×(1+k 2 )·5>0,且讨论直线AB 与圆C 1 相切时,可得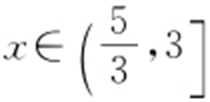 ,所以曲线c :x 2 +y 2 -3x =0,
,所以曲线c :x 2 +y 2 -3x =0,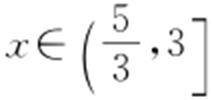 .
.
(3)存在.联立曲线c 与直线l 的方程,知 ⇒(1+k 2 )x 2 -(8k 2 +3)x +16k 2 =0.
⇒(1+k 2 )x 2 -(8k 2 +3)x +16k 2 =0.
①当l 与c 相切时,则有Δ =[-(8k 2 +3)]2 -4(1+k 2 )·16k 2 =0,即9-16k 2 =0,所以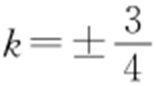 .代入联立后的方程,解得
.代入联立后的方程,解得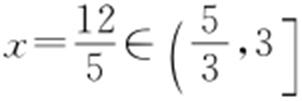 .
.

故 时,曲线c 与直线l 只有一个交点.
时,曲线c 与直线l 只有一个交点.
②当l 与c 相交时,如图所示,直线l 应被夹在直线PN 与直线QN 之间,则kl ∈(kPN ,kQN ),且PQ 关于x 轴对称,所以只需求出kQN .又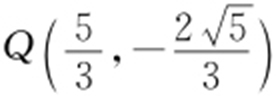 ,
,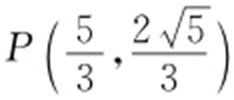 ,
,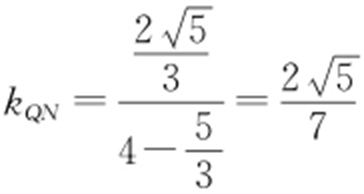 ,所以
,所以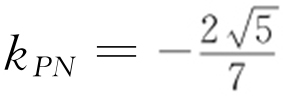 ,因此
,因此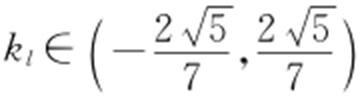 .综上,
.综上,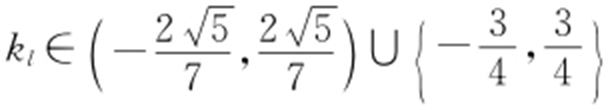 .
.
【例3 】(2014·安徽文·6) 过点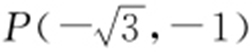 的直线l 与圆x 2 +y 2 =1有公共点,则直线l 的倾斜角的取值范围是( ).
的直线l 与圆x 2 +y 2 =1有公共点,则直线l 的倾斜角的取值范围是( ).
条件 (1)直线l 与圆有公共点⇒d ≤R .
(2)k =tanθ 的转化.
解析 (1)设过点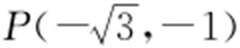 的直线为l :
的直线为l : .因为
.因为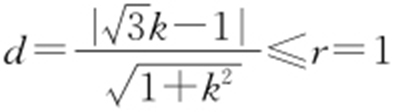 ,所以
,所以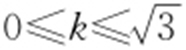 .
.
(2)当k 不存在时,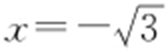 与x 2 +y 2 =1无交点,因此不符合.
与x 2 +y 2 =1无交点,因此不符合.
设直线l 的倾斜角为θ ,则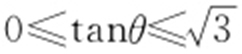 ,因此
,因此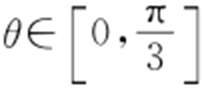 .故选:D.
.故选:D.
【例4 】(2013·重庆文·4) 设P 是圆(x -3)2 +(y +1)2 =4上的动点,Q 是直线x =-3上的动点,则|PQ |的最小值为( ).
A.6
B.4
C.3
D.2
条件 
解析 因为圆心到直线的距离d =6,R =2,所以|PQ |min =6-2=4.故选:B.
【例5 】(2015·吉安期中) 若圆(x -1)2 +(y +1)2 =R 2 上有且仅有两个点到直线4x +3y -11=0的距离等于1,则半径R 的取值范围是( ).
A.R >1
B.R <3
C.1<R <3
D.R ≠2
条件 等距点个数为2个⇒分界点法.
解析 因为圆心到直线的距离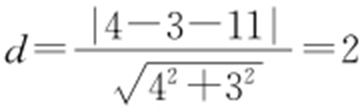 ,有且仅有两个点到直线4x +3y -11=0的距离等于1,所以|R -d |<1,即1<R <3.故选:C.
,有且仅有两个点到直线4x +3y -11=0的距离等于1,所以|R -d |<1,即1<R <3.故选:C.
总结
(1)直线与圆的位置关系判断的方法:①代数法;②几何法.
(2)
练习
1.(2012·安徽文·9) 若直线x -y +1=0与圆(x -a )2 +y 2 =2有公共点,则实数a 取值范围是( ).
A.[-3,-1]
B.[-1,3]
C.[-3,1]
D.(-∞,-3]∪[1,+∞)
2.(2015·新课标1文·20) 已知过点A (0,1)且斜率为k 的直线l 与圆C (x -2)2 +(y -3)2 =1交于M ,N 两点.
(1)求k 的取值范围;
(2)若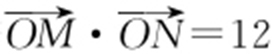 ,其中O 为坐标原点,求|MN |.
,其中O 为坐标原点,求|MN |.
3.(2014·华中师大附中月考) 求圆x 2 +y 2 -2x -2y +1=0上的动点Q 到直线3x +4y +8=0距离的最小值.
4.(2013·吉安一中月考) 若圆x 2 +y 2 -6x -2y +6=0上有且仅有三个点到直线ax -y +1=0(a 是实数)的距离为1,则a 等于( ).
考点3 弦长问题
例题
【例1 】(2012·北京文·9) 直线y =x 被圆x 2 +(y -2)2 =4截得弦长为 .
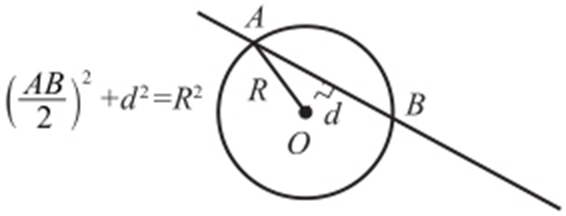
条件 弦心三角形.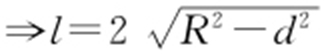 .
.
解析 因为圆心到直线的距离 ,R =2,所以
,R =2,所以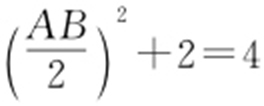 ,所以(AB )2 =8,即
,所以(AB )2 =8,即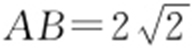 .
.
【例2 】(2014·重庆文理·14) 已知直线x -y +a =0与圆心为C 的圆x 2 +y 2 +2x -4y -4=0相交于A ,B 两点,且AC ⊥BC ,则实数a 的值为 .
条件 (1)BC 2 +AC 2 =AB 2 .
(2)利用等腰三角形⇒圆心到直线AB 的距离.
解析 易知圆心C (-1,2),R =3,所以知圆心C 到直线AB 的距离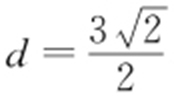 ,即
,即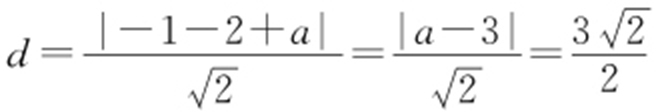 ,即|a -3|=3.所以a =0或a =6.
,即|a -3|=3.所以a =0或a =6.
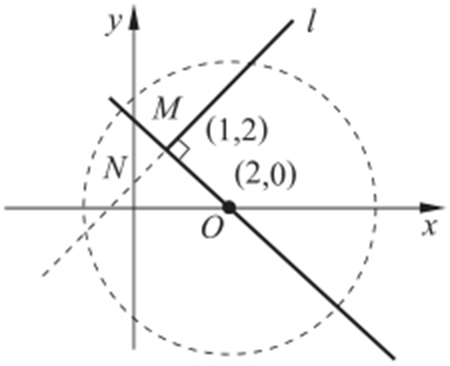
【例3 】(2015·定州期末) 过点M (1,2)的直线l 将圆(x -2)2 +y 2 =9分成两段弧,其中的劣弧最短时直线l 的方程为 .
条件 (1)劣弧最短⇒所对应的弦最短.
(2)过圆内一点的最长弦为直径,最短弦为过该点与直径垂直的弦.
解析 如图所示,易知kOM =-2,所以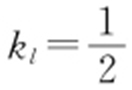 ,所以直线l 的方程为
,所以直线l 的方程为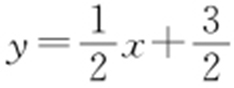 .
.
【例4 】(2014·福建理·6) 直线l :y =kx +1与圆O :x 2 +y 2 =1相交于A ,B 两点,则“k =1”是“△AOB 的面积为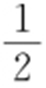 ”的( ).
”的( ).
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分又不必要条件
条件 (1)直线与圆相交,则d <R (d 是圆心到直线的距离).
(2) .
.
解析 圆心到直线的距离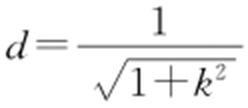 ,
,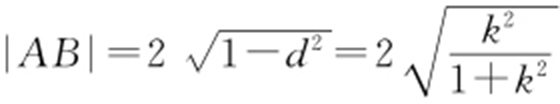 .
.
当k =1时,则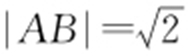 ,
,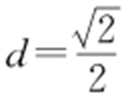 ,所以
,所以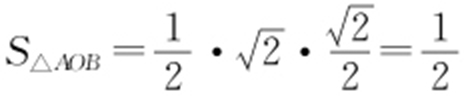 ,则充分性成立.若
,则充分性成立.若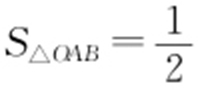 ,则
,则
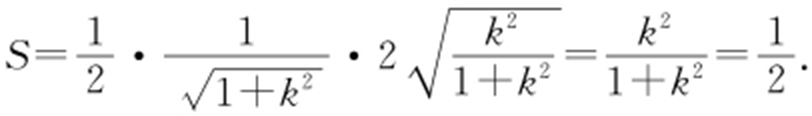
解得k =±1,则k =1不成立,即必要性不成立.
故k =1是△AOB 的面积为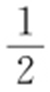 的充分不必要条件.故选:A.
的充分不必要条件.故选:A.
总结
(1)弦心三角形:.
(2)过圆内一点所作的弦最长是直径,最短弦是垂直于直径的弦.
练习
1.(2013·安徽文·6) 直线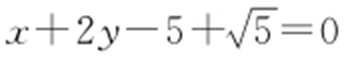 被圆x 2 +y 2 -2x -4y =0截得的弦长为( ).
被圆x 2 +y 2 -2x -4y =0截得的弦长为( ).
A.1
B.2
C.4
D.
2.(2015·湖南文·13) 若直线3x -4y +5=0与圆x 2 +y 2 =r 2 (r >0)相交于两点A ,B ,且∠AOB =120°(O 为坐标原点),则r = .
3.(2015·南通三模) P (2,-1)为圆(x -1)2 +y 2 =25的弦AB 的中点,则直线AB 的方程是( ).
A.x -y -3=0
B.2x +y -3=0
C.x +y -1=0
D.2x -y -5=0
4.(2016·新课标1文·15) 设直线y =x +2a 与圆C :x 2 +y 2 -2ay -2=0相交于A ,B 两点,若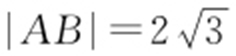 ,则圆C 的面积为 .
,则圆C 的面积为 .
考点4 切线问题
例题
【例1 】(2015·广东理·5) 平行于直线2x +y +1=0且与圆x 2 +y 2 =5相切的直线的方程是( ).
条件 (1)与直线ax +by +c =0平行的直线可设为ax +by +m =0.
(2)相切:圆心到直线距离等于半径.
解析 因为平行于直线2x +y +1=0,所以可设直线为2x +y +m =0.
又由与圆x 2 +y 2 =5相切可知,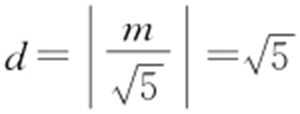 ,则m =±5,即直线为2x +y +5=0或2x +y -5=0.故选:D.
,则m =±5,即直线为2x +y +5=0或2x +y -5=0.故选:D.
【例2 】(2013·天津文·5) 已知过点P (2,2)的直线与圆(x -1)2 +y 2 =5相切,且与直线ax -y +1=0垂直,则a =( ).
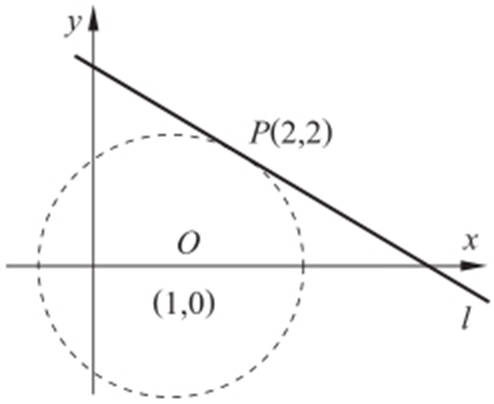
条件 (1)两直线垂直⇒k 1 k 2 =-1.
(2)点P 在圆上,且直线与圆相切.
解析 如图所示,易知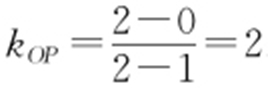 .
.
因为OP ⊥l ,所以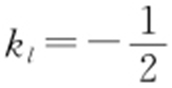 .又l 与直线ax -y +1=0垂直,因此,直线ax -y +1=0的斜率为2,所以a =2,故选:C.
.又l 与直线ax -y +1=0垂直,因此,直线ax -y +1=0的斜率为2,所以a =2,故选:C.
【例3 】(2015·重庆理·8) 已知直线l :x +ay -1=0(a ∈R )是圆O :x 2 +y 2 -4x -2y +1=0的对称轴,过点A (-4,a )作圆C 的一条切线,切点为B ,则|AB |=( ).
条件 (1)圆的对称轴为直径.
(2)切点三角形.
解析 因为直线x +ay -1=0是圆x 2 +y 2 -4x -2y +1=0的对称轴,所以直线x +ay -1=0经过圆心(2,1).则2+a -1=0,即a =-1.
所以A (-4,-1).如图所示,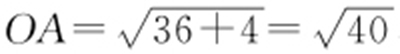 ,R =2,所以AB =6.故选:C.
,R =2,所以AB =6.故选:C.
总结
(1)平行线的设法;若l :ax +by +c =0,当l 1 //l 时,可设l 1 的方程为ax +by +m =0.
(2)两直线垂直,则k 1 k 2 =-1.
(3)圆的对称轴为直径.
(4)掌握弦切三角形的关系.
练习
1.(2015·安徽文·8) 直线3x +4y =b 与圆x 2 +y 2 -2x -2y +1=0相切,则b =( ).
A.-2或12
B.2或-12
C.-2或-12
D.2或12
2.(2015·山东理·9) 一条光线从点(-2,-3)射出,经y 轴反射与圆(x +3)2 +(y -2)2 =1相切,则反射光线所在的直线的斜率为( ).
3.(2015·山东文·13) 过点P 作x 2 +y 2 =1的切线,切点分别为A ,B ,则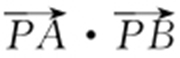 = .
= .
考点5 圆与圆的位置关系
例题
(2014·湖北文·6) 若圆C 1 :x 2 +y 2 =1与圆C 2 :x 2 +y 2 -6x -8y +m =0外切,则m =( ).
A.21
B.19
C.9
D.-11
条件 两圆外切⇒d =R 1 +R 2 .
解析 因为C 1 的圆心为(0,0),R 1 =1,C 2 的圆心为(3,4),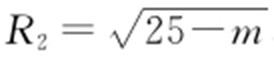 ,且有
,且有 ,则由
,则由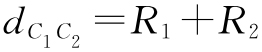 知,
知,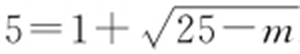 .故25-m =16,即m =9.故选:C.
.故25-m =16,即m =9.故选:C.
总结
两圆的位置关系可全部转化成点与点的距离问题.
练习
(2016·山东文·7) 已知圆M :x 2 +y 2 -2ay =0(a >0)截直线x +y =0所得线段的长度是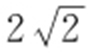 ,则圆M 与圆N :(x -1)2 +(y -1)2 =1的位置关系是( ).
,则圆M 与圆N :(x -1)2 +(y -1)2 =1的位置关系是( ).
A.内切
B.相交
C.外切
D.相离
优秀是一种习惯,不优秀也是一种习惯,那为什么不一直优秀下去!
——萌萌(王勇老师)
创新的源泉在于你相信:但凡有生命的事情,一定有比当下更有效的办法.
——萌萌(王勇老师)
停下来想想你是不是正在努力把你的青春献给了money而不是dream.
——萌萌(王勇老师)
想学好数学,你最好拿出你八卦时的那份激情!
——萌萌(王勇老师)
我希望我的学生不要被我深深的内涵所吸引,而要被我帅气的外表所折服!毕竟学好数学的第一步就是喜欢上你的数学老师.
——萌萌(王勇老师)
寻求题目的解法道路是寂寞的,但是每一个分叉路口都有惊喜,请举起手机拍一下沿途的风景.
——萌萌(王勇老师)
很多时候,乐观的态度和好听的话帮不了你.
——冷冷的隆兄(袁龙老师)
又一天过去了,今天过得怎么样,梦想是不是更远了?
——冷冷的隆兄(袁龙老师)
回首青春,我发现自己失去了很多宝贵的东西.但我并不难过,因为我知道,以后会失去的更多.
——冷冷的隆兄(袁龙老师)
秋天是收获的季节.别人的收获是成功与快乐,你的收获是认识到并不是每个人都会成功与快乐.
——冷冷的隆兄(袁龙老师)
你只需看着别人退步,因为你在进步;还是你看着别人进步,因为你在退步!
——冷冷的隆兄(袁龙老师)
你努力后的成功,难道不能弥补你成功前的痛苦?
哦!那也许是你还没体会过成功!
——冷冷的隆兄(袁龙老师)
假如今天数学伤害了你,不要悲伤,不要哭泣,因为明天数学还会继续伤害你.
——冷冷的隆兄(袁龙老师)
你努力后的成功,难道不能弥补你成功前的痛苦?
哦!那也许是你还没体会过成功!
——冷冷的隆兄(袁龙老师)









