第7章　参数方程与极坐标

1．过定点（x ₀ ，y ₀ ），倾角为α 的直线的参数方程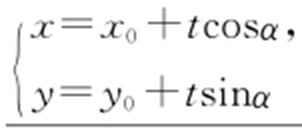： （t 为参数） ，其中参数t 是以定点P (x ₀ ，y ₀ )为起点，对应于t 点M (x ，y )为终点的有向线段PM 的数量，又称为点P 与点M 间的有向距离．

根据t 的几何意义，有以下结论．

（1）设A ，B 是直线上任意两点，它们对应的参数分别为t_A 和t_B ，则|AB |=|t_A -t_B | ．

（2）线段AB 的中点所对应的参数值等于 ．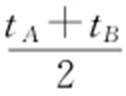

2．中心在（x ₀ ，y ₀ ），半径等于r 的圆参数方程为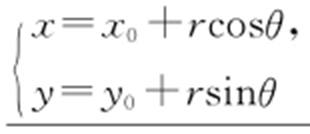 （θ 为参数） ．

3．中心在原点，焦点在x 轴（或y 轴）上的椭圆参数方程为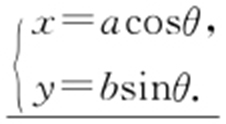

4．极坐标与直角坐标互化的前提条件：

（1）极点与原点重合；

（2）极轴与x 轴正方向重合；

（3）取相同的单位长度．

设点P 的直角坐标为（x ，y ），它的极坐标为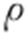（ ，θ ），则

（1）

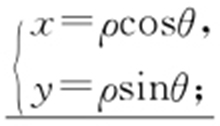
（2） ．

若把直角坐标化为极坐标，求极角时，应注意判断点P 所在的象限（即角的终边的位置），以便正确地求出角．

一、参数方程

考点1　直线

例题

【例1 】（2014·湖南文·11）　在平面直角坐标系中，曲线C 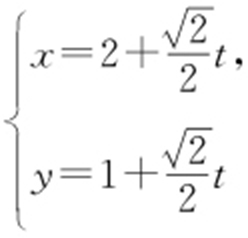： （t 为参数）的普通方程为 ．

条件 　利用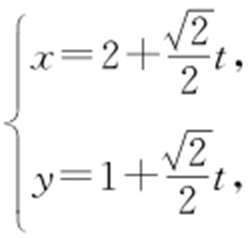 转化为直线的参数方程 （θ 为直线倾斜角，t 为参数）．

解析 　消去参数t 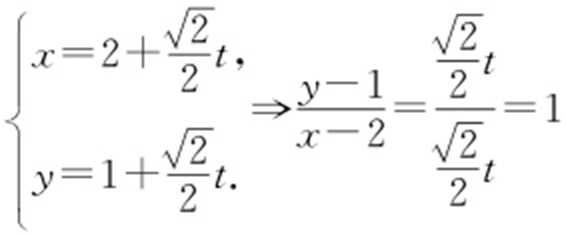． ．所以y -1=x -2⇒x -y -1=0．

【例2 】（2008·安徽模考）　已知椭圆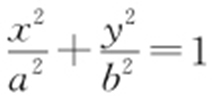 ，c =2，b =2，已知过点（-2，0）的直线倾斜角为θ ，交椭圆于A ，B 两点，求证 ．

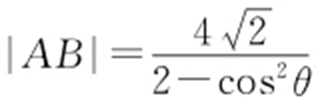条件 　（1）c =2，b =2．求出椭圆方程．

（2）过（-2，0）的直线倾斜角为θ 转化为参数方程：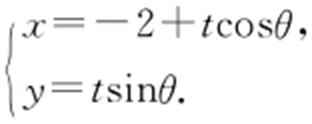

（3）理解直线的参数方程中t 的含义．

解析 　求出椭圆方程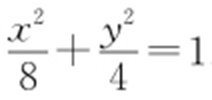： ．设过（-2，0）的参数方程为 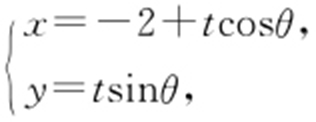代入椭圆方程，得 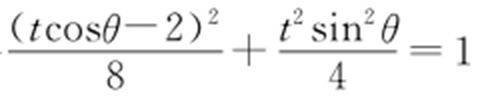，即t ² cos² θ +4-4cosθt +2sin² θt ² -8=0，(1+sin² θ )t ² -4cosθt -4=0，则 ．

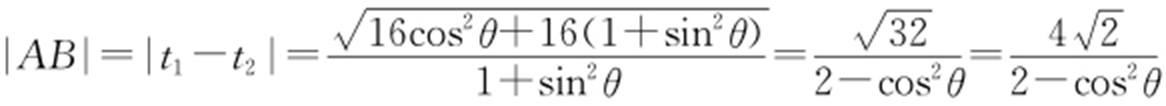总结

学会判断，化简，建立直线的参数方程．

练习

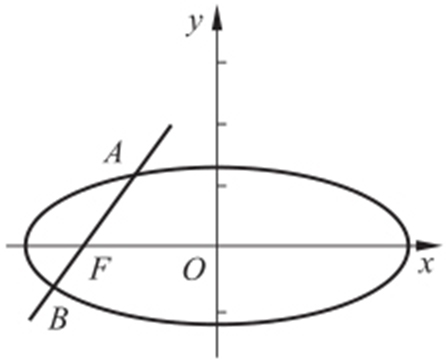
（2010·辽宁模考）　设椭圆C ： （a ＞b ＞0）的左焦点为F ，过点F 的直线l 与椭圆C 相交于A ，B 两点，直线l 的倾斜角为60°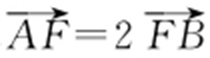， ．（1）求椭圆C 的离心率；（2）如果 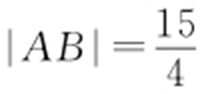，求椭圆C 的方程．

考点2　圆

例题

【例 】（2012·湖南理·9）　在直角坐标系xOy 中，已知曲线C ₁ 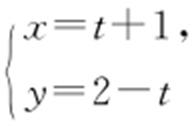： 与曲线C ₂ 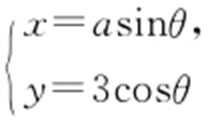： （θ 为参数，a ＞0）有一个公共点在x 轴上，则a 等于 ．

条件 　 ， ．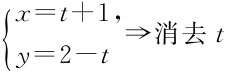

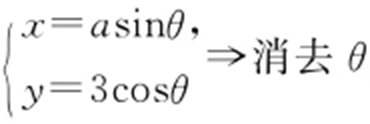解析 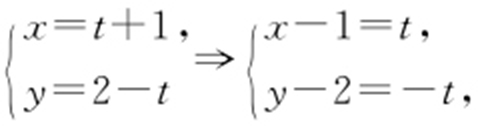　 则 ，所以y -2=1-x ，x +y -3=0与x 轴交点（3，0）． ．

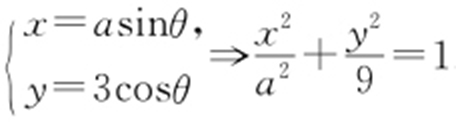将（3，0）代入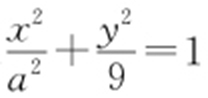 ，得a ² =9，所以由a ＞0可得a =3．

总结

区分直线与圆的参数方程．会消去圆的参数方程的参数θ ．

练习

（2012·重庆理·8）　直线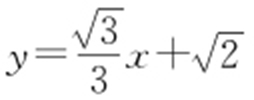 与圆心为D 的圆 （θ ∈[0，2π)）交于A ，B 两点，则直线AD 与BD 的倾斜角之和为（　　）．

考点3　其他曲线

例题

【例1 】（2013·陕西文·15）　圆锥曲线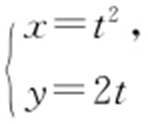 （t 为参数）的焦点坐标是 ．

条件 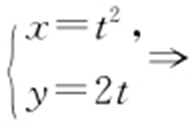　 消去参数t ．

解析 　 ，所以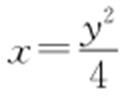 ，即y ² =4x ，为抛物线，焦点为（1，0）．

【例2 】（2014·新课标1文理·23）　已知曲线C 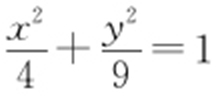： ，直线l 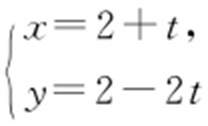： （t 为参数）．

（1）写出曲线C 的参数方程，直线l 的普通方程；

（2）过曲线C 上任一点P 作与l 夹角为30°的直线，交l 于点A ，求|PA |的最大值与最小值．

条件 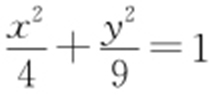　 转化为参数方程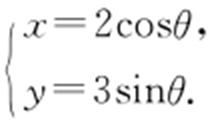： 利用参数方程．求椭圆上任一点到直线距离．

解析 　 ．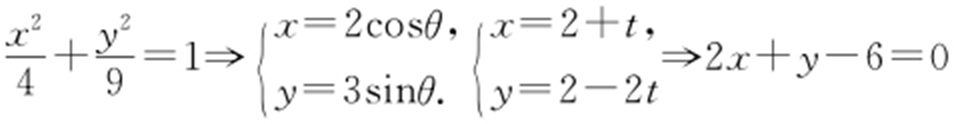

P (2cosθ ，3sinθ )为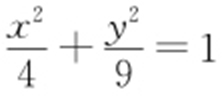 上任意一点，则P 到l 的距离 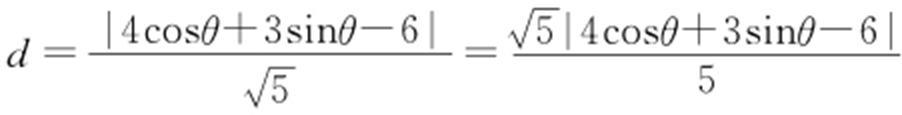， ，即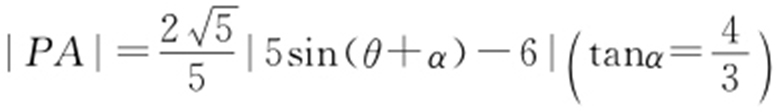 ．取sin(θ +α )=-1，则|PA |取最大值 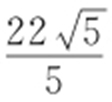，取sin(θ +α )=1，则|PA |取最小值 ．

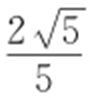总结

熟练利用参数方程处理最值问题，结合三角函数内容并巩固复习．

练习

（2014·辽宁文理·23）　将圆x ² +y ² =1上每一点的横坐标保持不变，纵坐标变为原来的2倍，得曲线C ．

（1）写出C 的参数方程；

（2）设直线l ：2x +y -2=0与C 的交点为P ₁ ，P ₂ ，以坐标原点为极点，x 轴正半轴为极坐标建立极坐标系，求过线段P ₁ P ₂ 的中点且与l 垂直的直线的极坐标方程．

考点4　参数方程的应用最值问题

例题

【例1 】（2014·南昌月考）　设P 是椭圆2x ² +3y ² =12上的一个动点，则x +2y 的最大值是 ，最小值是 ．

条件 　2x ² +3y ² =12⇒参数方程，代入x +2y ．

解析 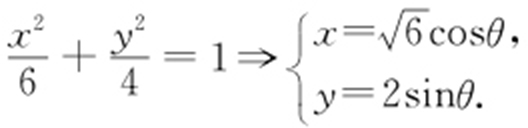　 将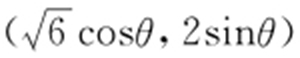 代入x +2y ，得 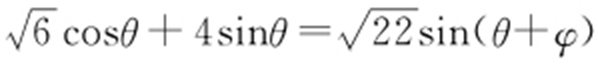，故最大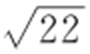值为 ，最小值为 ．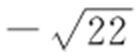

【例2 】（2015·南昌调研考）　已知曲线C 的参数方程为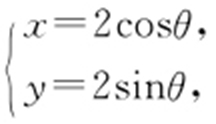 以极点为原点、极轴为x 轴的正半轴建立平面直角坐标系，直线l 的参数方程为 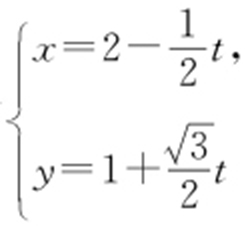（t 为参数）．

（1）写出直线l 与曲线C 的直角坐标系下的方程；

（2）设曲线C 经过伸缩变换 得到曲线C′ ，设曲线C′ 上任一点为M (x ₀ ，y ₀ )，求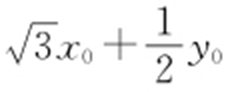 的取值范围．

条件 　 消去参数θ 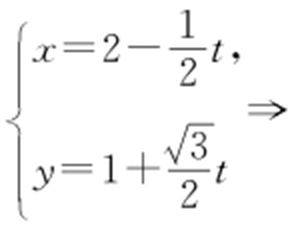． 消去参数t 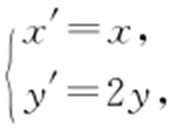． 复习坐标变换．

解析 　（1） ．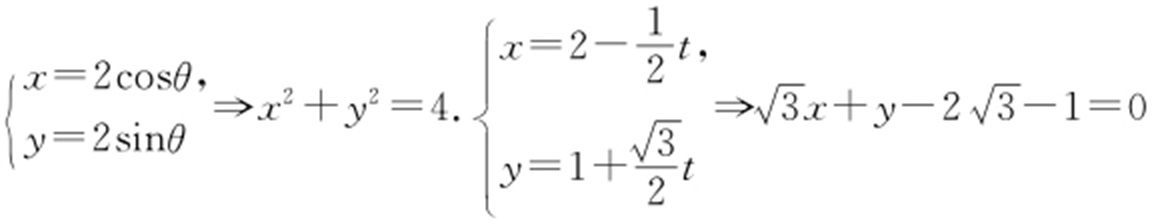

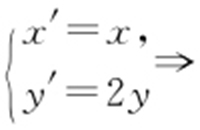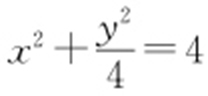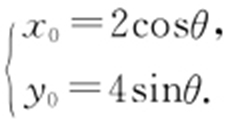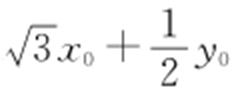（2） 坐标变换： ．M 的参数方程为 代入 ，得 ．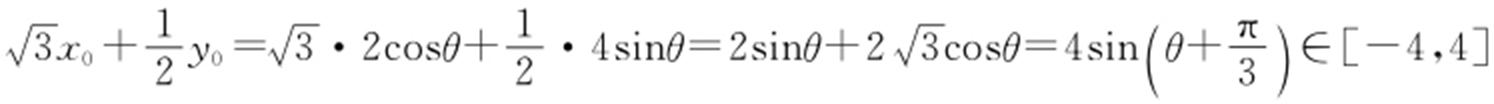

总结

利用参数方程去解决曲线上各点的最值问题，回顾三角函数化简．

练习

（2014·全国卷1文理·23改编）　已知曲线C 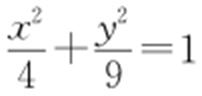： ，直线l 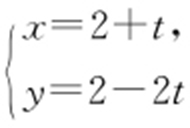： （t 为参数）．过曲线C 上任意一点P 作直线，交l 于点A ，求|PA |的最大值与最小值．

二、极坐标

考点1　直线

例题

【例 】（2015·北京理·11）　在极坐标系中，点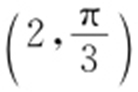 到直线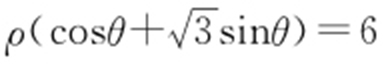 的距离为 ．

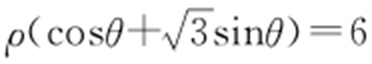条件 　 转化为直角坐标， 转化为直角坐标下的方程．

解析 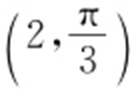　 转化为 ， ，则 ．故 ．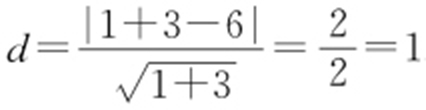

总结

熟记用 进行转化．

练习

（2015·广东理·14）　已知直线l 的极坐标方程为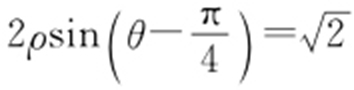 ，点A 的极坐标为 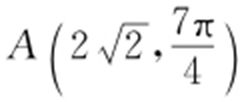，则点A 到直线l 的距离为 ．

考点2　圆

例题

【例1 】（2011·江西理·15）　若曲线的极坐标方程为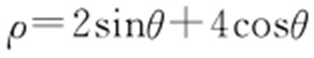 ，以极点为原点、极轴为x 轴正半轴建立直角坐标系，则该曲线的直角坐标方程为 ．

条件 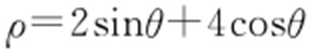　 转化为直角坐标．

解析 　 ，所以方程为x ² +y ² =2y +4x ．

【例2 】（2011·北京理·3）　在极坐标系中，圆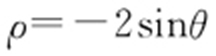 的圆心的极坐标是（　　）．

条件 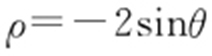　 ，等号两边同时乘以 ．

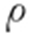解析 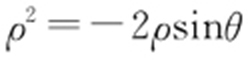　 ．x ² +y ² =-2y ，则x ² +y ² +2y =0，即x ² +(y +1)² =1，故圆心坐标为（0，-1），极坐标为 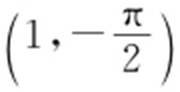．故选：B．

总结

熟记用 进行坐标转换．

练习

1．（2012·湖南文·10）　在极坐标系中，曲线C ₁ 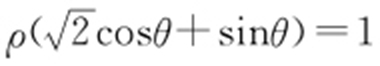： 与曲线C ₂ 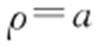： （a ＞0）的一个交点在极轴上，则a = ．

2．（2013·安徽理·7）　在极坐标系中，圆 的垂直于极轴的两条切线方程分别为（　　）．

三、综合

例题

【例1 】（2015·安徽理·12）　在极坐标中，圆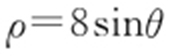 上的点到直线 距离的最大值是 ．

条件 　方程两边同时乘以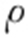 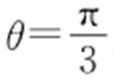， 化为标准方程．

解析 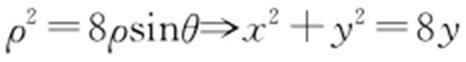　 ，即x ² +(y -4)² =16，圆心为（0，4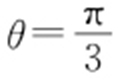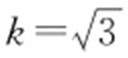）． ， ，过原点，得 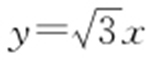．（0，4）到 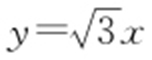距离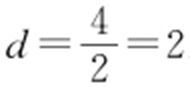 ．d _max =2+4=6．

【例2 】（2015·新课标1理文·23）　在直角坐标系xOy 中，直线C ₁ ：x =-2，圆C ₂ ：(x -1)² +(y -2)² =1，以坐标原点为极点、x 轴的正半轴为极轴建立极坐标系．

（1）求C ₁ ，C ₂ 的极坐标方程；

（2）若直线C ₃ 的极坐标方程为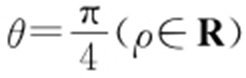 ，设C ₂ 与C ₃ 的交点为M ，N ，求△C ₂ MN 的面积．

条件 　利用 进行转换．

解析 　（1）C ₁ ：x =-2，即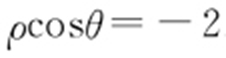 ．C ₂ ：(x -1)² +(y -2)² =1，即 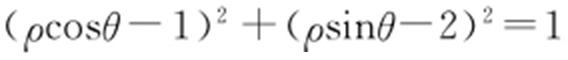，化简得 ．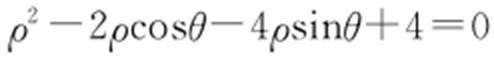

（2）C ₃ 的极坐标方程为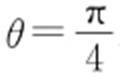 ．代入C ₂ 的方程得 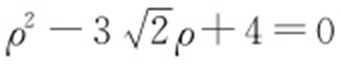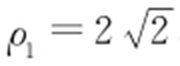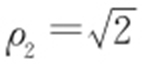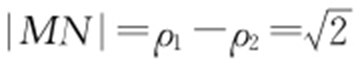， ， ， ．C ₂ 圆的半径为1，C ₂ M ⊥C ₁ N ，所以 ．

【例3 】（2016·新课标1文理·23）　在直角坐标系xOy 中，曲线C ₁ 的参数方程为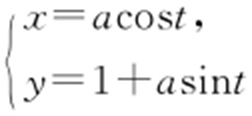 （t 为参数，a ＞0）．在以坐标原点为极点、x 轴正半轴为极轴的极坐标系中，曲线C ₂ ： ．

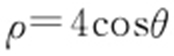（1）说明C ₁ 是哪种曲线，并将C ₁ 的方程化为极坐标方程；

（2）直线C ₃ 的极坐标方程为θ =α ₀ ，其中α ₀ 满足tanα ₀ =2，若曲线C ₁ 与C ₂ 的公共点都在C ₃ 上，求α ．

条件 　（1）参数方程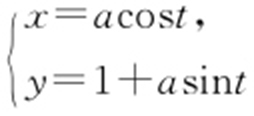 化为标准方程，再化为极坐标方程．

（2）利用直角坐标系解决公共弦问题．

解析 　（1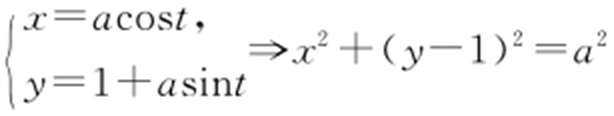） 为圆．

化为一般式：x ² +y ² -2y +1-a ² =0．化为极坐标方程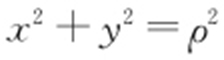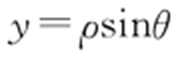： ， ．即 ．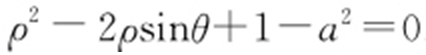

（2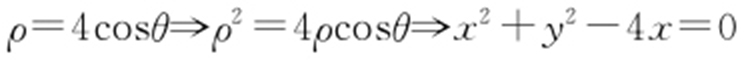） ，即(x -2)² +y ² =4．C ₃ ：θ =α ₀ ，tanα ₀ =2，则y =2x ．x ² +y ² -2y +1-a ² =0减去x ² +y ² -4x =0，即4x -2y +1-a ² =0，与y =2x 一致，所以a ² =1，则a =1（a ＞0）．

【例4 】（2015·湖南理·16）　已知直线l 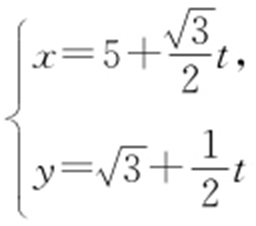： （t 为参数），以坐标原点为极点、x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为 ．

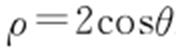（1）将曲线C 的极坐标方程化为直角坐标方程；

（2）设点M 的直角坐标为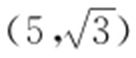 ，直线l 与曲线C 的交点为A ，B ，求|MA |·|MB |的值．

条件 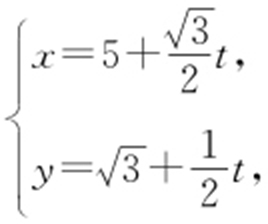　 消去t ．对 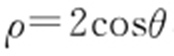，两边同时乘以 ．

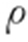解析 　（1）将极坐标方程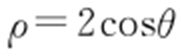 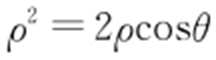， ，化为直角坐标方程，得x ² +y ² =2x ，即(x -1)² +y ² =1．

（2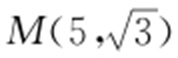） 恰在直线上，将l 的参数方程 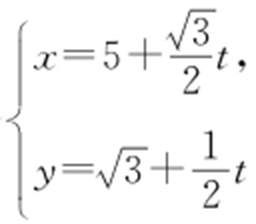代入x ² +y ² =2x ，得 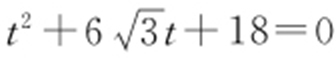，则|MA |·|MB |=|t ₁ |·|t ₂ |=|18|=18．

总结

极坐标、参数方程以及标准方程间相互转化时，注意化简技巧，并且理解参数方程中t 的含义．

练习

1．（2015·新课标2文理·23）　在直角坐标系xOy 中，曲线C ₁ 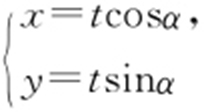： （t 为参数，t ≠0），其中0≤α ＜π，在以O 为极点、x 轴正半轴为极轴的极坐标系中，曲线C ₂ 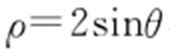： ，C ₃ ： ．

（1）求C ₂ 与C ₃ 交点的直角坐标；

（2）若C ₁ 与C ₂ 相交于点A ，C ₁ 与C ₃ 相交于点B ，求|AB |的最大值．

2．（2016·新课标3文理·23）　在直角坐标系xOy 中，曲线C ₁ 的参数方程为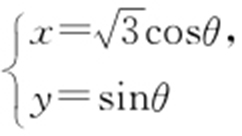 （θ 为参数），以坐标原点为极点、以x 轴的正半轴为极轴，建立极坐标系，曲线C ₂ 的极坐标方程为 ．

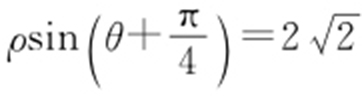（1）写出C ₁ 的普通方程和C ₂ 的直角坐标方程；

（2）设点P 在C ₁ 上，点Q 在C ₂ 上，求|PQ |的最小值及此时P 的直角坐标．

3．（2016·江苏理·21）　在平面直角坐标系xOy 中，已知直线l 的参数方程为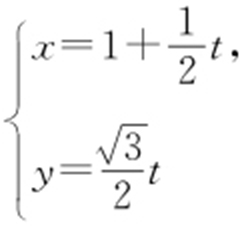 （t 为参数），椭圆C 的参数方程为 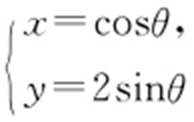（θ 为参数）．设直线l 与椭圆C 相交于A ，B 两点，求线段AB 的长．

当你疲惫的时候，停下脚步，看看大冬天里在路边的摊贩，想想你未来的生活，这个时候也许你会想清楚人生的意义．

——江润涛老师

考完你会兴奋一秒，考后你会怀念一世．

——江润涛老师

一场考试，四张试卷，拼了三年，一个夏天．

——江润涛老师

你们所厌恶的今天，是我们永远回不去的昨天．

——江润涛老师

下个夏天，教室里还会坐满了人，可惜，不再是我们．

——江润涛老师

高考最迷人的地方不是如愿以偿，而是阴差阳错．

——江润涛老师

如果你不想做一个碌碌无为的自己，从现在开始奋斗，直到结束的那一刻，你可以骄傲地告诉自己，青春无悔．

——江润涛老师

我们不能主宰生命的长度，但是我们可以主宰生命的价值．

——江润涛老师

百日冲刺，你需要做到的只是心无旁骛，全力以赴．

——江润涛老师

同学们，现在这个看脸的时代，才华也是不能少的，因为将来的时代既要才华又要看脸．

——B超（吕超老师）

梦想在天边，努力在手边．

——B超（吕超老师）

一模二模三模，和高考是两回事，差100分的人也是有的，就是我．

——B超（吕超老师）

走向高考的这条路，从来不是一帆风顺，遇到点挫折，抬起头，努力到考上的最后一刻钟．

——B超（吕超老师）