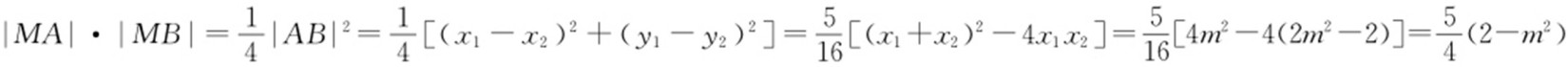【考点 】 直线与椭圆等基础知识.
51.(1)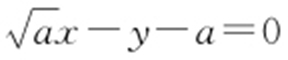 或
或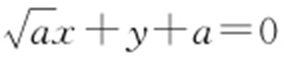 ;(2)存在.
;(2)存在.
【解析 】 (1)由题设可得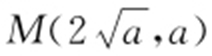 ,
,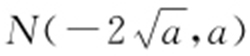 ,或
,或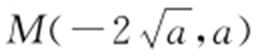 ,
, .
.
因为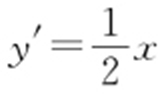 ,故
,故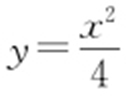 在
在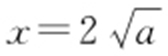 处的倒数值为
处的倒数值为 ,C 在
,C 在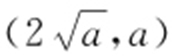 处的切线方程为
处的切线方程为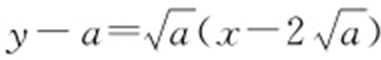 ,即
,即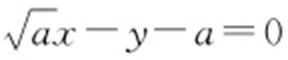 ,故
,故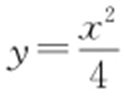 在
在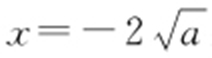 处的倒数值为
处的倒数值为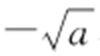 ,C 在
,C 在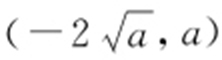 处的切线方程为
处的切线方程为 ,即
,即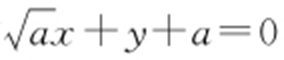 ,故所求切线方程为
,故所求切线方程为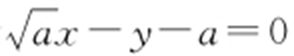 或
或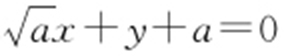 .
.
(2)存在符合题意的点,证明如下:
设P (0,b )为符合题意的点,M (x 1 ,y 1 ),N (x 2 ,y 2 ),直线PM ,PN 的斜率分别为k 1 ,k 2 .将y =kx +a 代入C 的方程,整理得x 2 -4kx -4a =0.所以x 1 +x 2 =4k ,x 1 x 2 =-4a ,所以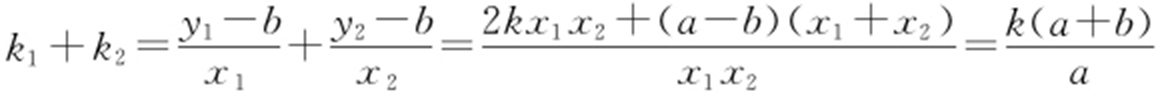 .
.
当b =-a 时,有k 1 +k 2 =0,则直线PM 的倾斜角与直线PN 的倾斜角互补,故∠OPM =∠OPN ,所以P (0,-a )符合题意.
【考点 】 抛物线的切线;直线与抛物线的位置关系.
52.(1)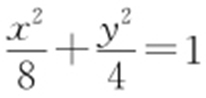 ;(2)为定值
;(2)为定值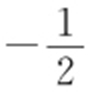 .
.
【解析 】 (1)由题设得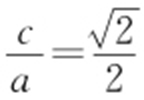 ,又知点的坐标满足椭圆的方程,所以
,又知点的坐标满足椭圆的方程,所以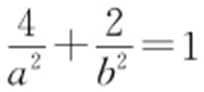 ,联立解得a 2 =8,b 2 =4,所以切线C 的方程为
,联立解得a 2 =8,b 2 =4,所以切线C 的方程为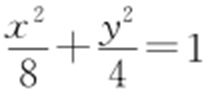 .
.
(2)设A ,B 两点的坐标为(x 1 ,y 1 ),(x 2 ,y 2 ),点M 的坐标为(m ,n ),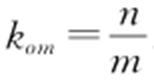 .则
.则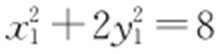 ,
,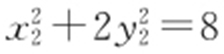 ,上面两个式子相减,得
,上面两个式子相减,得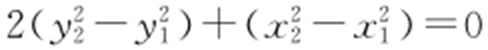 ,变形得
,变形得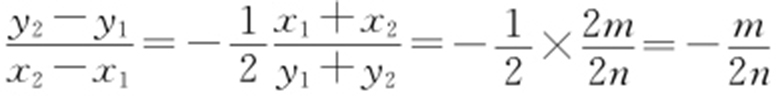 ,所以
,所以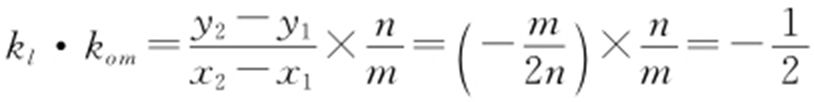 (定值).
(定值).
【考点 】 直线与椭圆的相交问题;中点弦问题.
53.(1)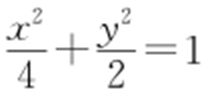 ;(2)
;(2)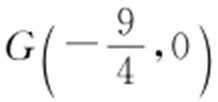 在以AB 为直径的圆外.
在以AB 为直径的圆外.
【解析 】 解法1:(1)由已知得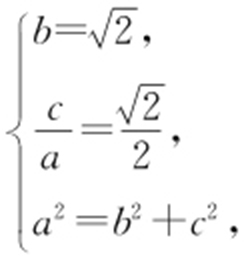 解得
解得 所以椭圆E 的方程为
所以椭圆E 的方程为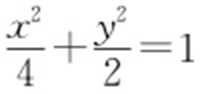 .
.
(2)设点A (x 1 ,y 1 ),B (x 2 ,y 2 ),AB 中点为H (x 0 ,y 0 ).
由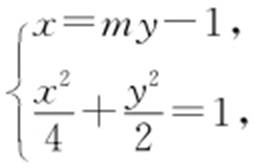 得(m 2 +2)y 2 -2my -3=0,所以
得(m 2 +2)y 2 -2my -3=0,所以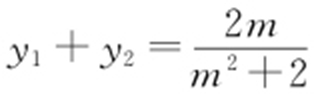 ,
,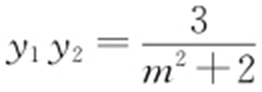 ,从而
,从而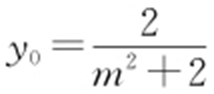 ,所以
,所以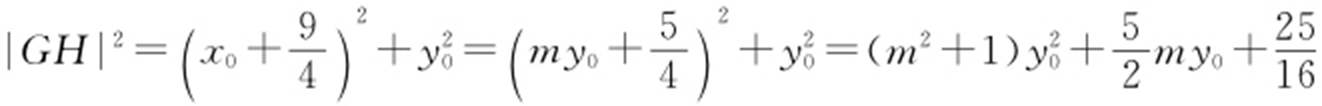 .
.
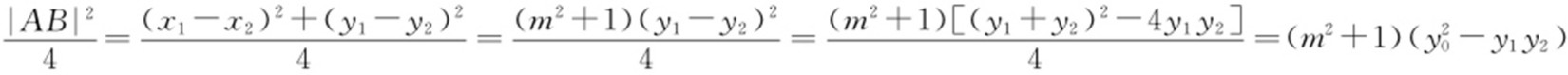 ,
,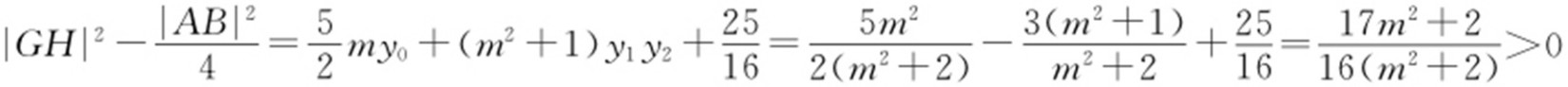 ,所以
,所以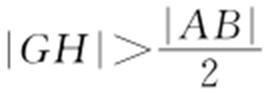 ,故
,故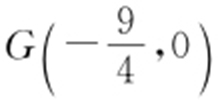 在以AB 为直径的圆外.
在以AB 为直径的圆外.
解法2:(1)同解法1.
(2)设点A (x 1 ,y 1 ),B (x 2 ,y 2 ),则 ,
,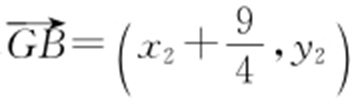 .
.
由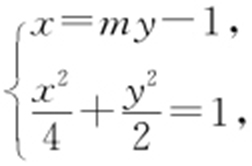 得(m 2 +2)y 2 -2my -3=0,所以
得(m 2 +2)y 2 -2my -3=0,所以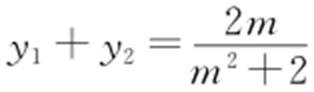 ,
,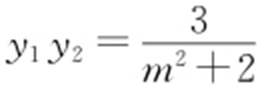 ,从而
,从而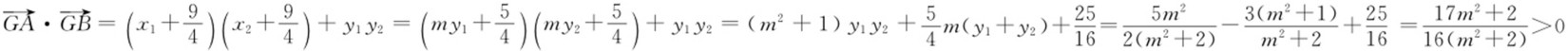 ,所以
,所以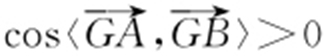 .又
.又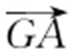 ,
,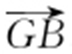 不共线,所以∠AGB 为锐角.故点
不共线,所以∠AGB 为锐角.故点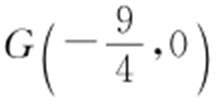 在以AB 为直径的圆外.
在以AB 为直径的圆外.
【考点 】 椭圆的标准方程;直线和椭圆的位置关系;点和圆的位置关系.
54.(1)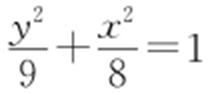 ;(2)
;(2)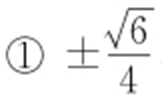 ,②详见解析.
,②详见解析.
【解析 】 (1)由C 1 :x 2 =4y 知其焦点F 的坐标为(0,1),因为F 也是椭圆C 2 的一焦点,所以a 2 -b 2 =1①,又C 1 与C 2 的公共弦的长为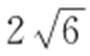 ,C 1 与C 2 都关于y 轴对称,且C 1 的方程为x 2 =4y ,由此易知C 1 与C 2 的公共点的坐标为
,C 1 与C 2 都关于y 轴对称,且C 1 的方程为x 2 =4y ,由此易知C 1 与C 2 的公共点的坐标为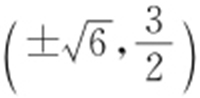 ,所以
,所以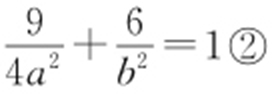 ,联立①,②,得a 2 =9,b 2 =8,故C 2 的方程为
,联立①,②,得a 2 =9,b 2 =8,故C 2 的方程为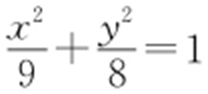 .
.
(2)A (x 1 ,y 1 ),B (x 2 ,y 2 ),C (x 3 ,y 3 ),D (x 4 ,y 4 ).
因为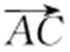 与
与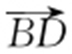 同向,且|AC |=|BD |,所以
同向,且|AC |=|BD |,所以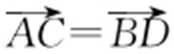 ,从而x 3 -x 1 =x 4 -x 2 ,即x 1 -x 2 =x 3 -x 4 ,于是(x 1 +x 2 )2 -4x 1 x 2 =(x 3 +x 4 )2 -4x 3 x 4 ③,设直线l 的斜率为k ,则l 的方程为y =kx +1,由
,从而x 3 -x 1 =x 4 -x 2 ,即x 1 -x 2 =x 3 -x 4 ,于是(x 1 +x 2 )2 -4x 1 x 2 =(x 3 +x 4 )2 -4x 3 x 4 ③,设直线l 的斜率为k ,则l 的方程为y =kx +1,由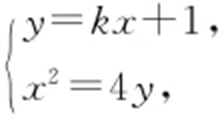 得x 2 +16kx -64=0,而x 1 ,x 2 是这个方程的两根,所以x 1 +x 2 =4k ,x 1 x 2 =-4④,由
得x 2 +16kx -64=0,而x 1 ,x 2 是这个方程的两根,所以x 1 +x 2 =4k ,x 1 x 2 =-4④,由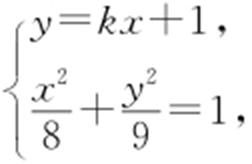 得(9+8k 2 )x 2 +16kx -64=0,而x 3 ,x 4 是这个方程的两根,所以
得(9+8k 2 )x 2 +16kx -64=0,而x 3 ,x 4 是这个方程的两根,所以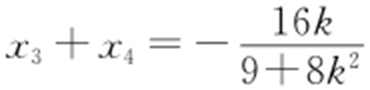 ,
,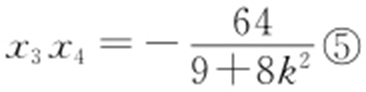 ,将④,⑤代入③,得
,将④,⑤代入③,得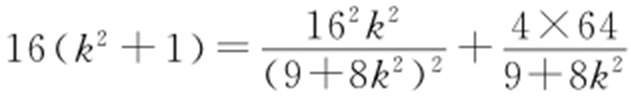 ,即
,即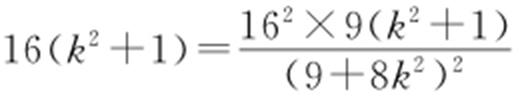 ,所以(9+8k 2 )2 =16×9,解得
,所以(9+8k 2 )2 =16×9,解得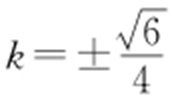 ,即直线l 的斜率为
,即直线l 的斜率为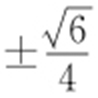 .
.
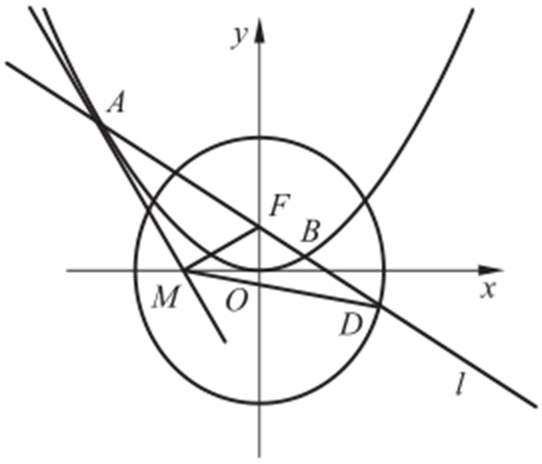
②由x 2 =4y ,得 ,所以C 1 在点A 处的切线方程为
,所以C 1 在点A 处的切线方程为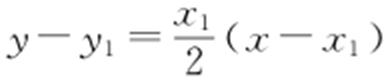 ,即
,即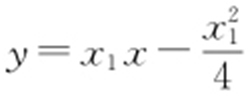 ,令y =0,得
,令y =0,得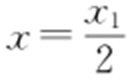 ,即
,即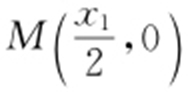 ,所以
,所以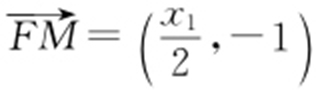 ,而
,而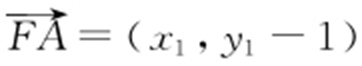 ,于是
,于是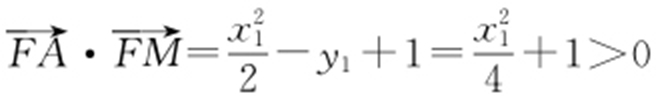 ,因此∠AFM 是锐角,从而∠MFD =180°-∠AFM 是钝角,故直线l 绕点F 旋转时,△MFD 总是钝角三角形.
,因此∠AFM 是锐角,从而∠MFD =180°-∠AFM 是钝角,故直线l 绕点F 旋转时,△MFD 总是钝角三角形.
【考点 】 椭圆的标准方程及其几何性质;直线与椭圆的位置关系.
55.(1)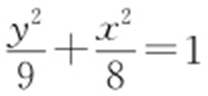 ;(2)
;(2)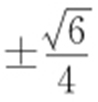 .
.
【解析 】 (1)由C 1 :x 2 =4y ,知其焦点F 的坐标为(0,1),因为F 也是椭圆C 2 的一个焦点,所以a 2 -b 2 =1①.又C 1 与C 2 的公共弦长为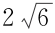 ,C 1 与C 2 都关于y 轴对称,且C 1 的方程为C 1 :x 2 =4y ,由此易知C 1 与C 2 的公共点的坐标为
,C 1 与C 2 都关于y 轴对称,且C 1 的方程为C 1 :x 2 =4y ,由此易知C 1 与C 2 的公共点的坐标为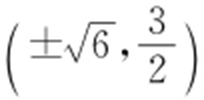 ,所以
,所以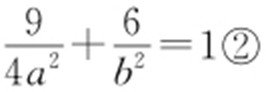 .联立①,②,得a 2 =9,b 2 =8,故C 2 的方程为
.联立①,②,得a 2 =9,b 2 =8,故C 2 的方程为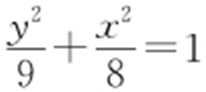 .
.
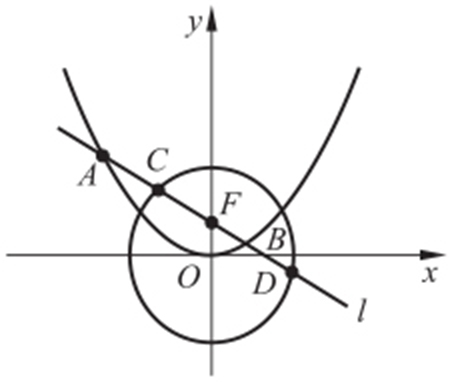
(2)如图,设A (x 1 ,y 1 ),B (x 2 ,y 2 ),C (x 3 ,y 3 ),D (x 4 ,y 4 ),因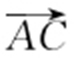 与
与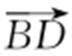 同向,且|AC |=|BD |,所以
同向,且|AC |=|BD |,所以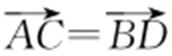 ,从而x 3 -x 1 =x 4 -x 2 ,即x 3 -x 4 =x 1 -x 2 ,于是(x 3 +x 4 )2 -4x 3 x 4 =(x 1 +x 2 )2 -4x 1 x 2 ③.
,从而x 3 -x 1 =x 4 -x 2 ,即x 3 -x 4 =x 1 -x 2 ,于是(x 3 +x 4 )2 -4x 3 x 4 =(x 1 +x 2 )2 -4x 1 x 2 ③.
设直线l 的斜率为k ,则l 的方程为y =kx +1.由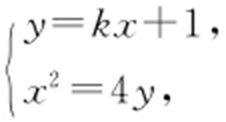 得x 2 -4kx -4=0,由x 1 ,x 2 是这个方程的两根,得x 1 +x 2 =4k ,x 1 x 2 =-4④.由
得x 2 -4kx -4=0,由x 1 ,x 2 是这个方程的两根,得x 1 +x 2 =4k ,x 1 x 2 =-4④.由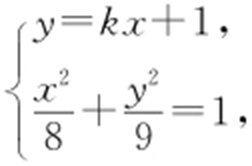 得(9+8k 2 )x 2 +16kx -64=0,而x 3 ,x 4 是这个方 程的两根,故
得(9+8k 2 )x 2 +16kx -64=0,而x 3 ,x 4 是这个方 程的两根,故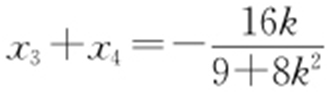 ,
,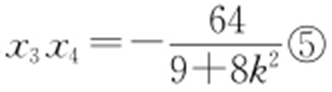 ,将④,⑤代入③,得
,将④,⑤代入③,得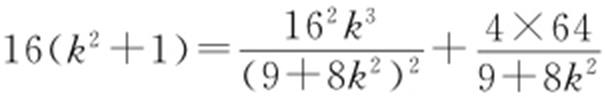 ,即
,即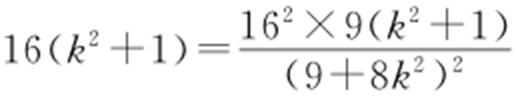 ,所以(9+8k 2 )2 =16×9,解得
,所以(9+8k 2 )2 =16×9,解得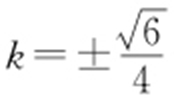 ,即直线l 的斜率为
,即直线l 的斜率为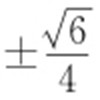 .
.
【考点 】 直线与圆锥曲线的位置关系;椭圆的几何性质.
极坐标与参数方程
56.6.
【考点 】 极坐标与直角坐标的互化;点到直线的距离.
57.1.
【解析 】 先把点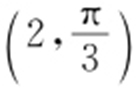 的极坐标化为直角坐标
的极坐标化为直角坐标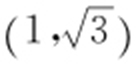 ,再把直线的极坐标方程
,再把直线的极坐标方程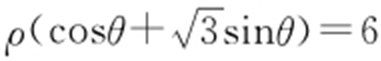 化为直角坐标方程
化为直角坐标方程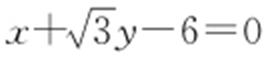 ,利用点到直线距离公式,得
,利用点到直线距离公式,得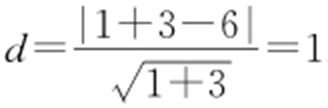 .
.
【考点 】 极坐标与直角坐标的互化;点到直线的距离.
58.x 2 +(y -1)2 =1.
【解析 】 将极坐标化为直角坐标,求解即可.
曲线C 的极坐标方程为 ,所以
,所以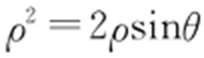 ,它的直角坐标方程为x 2 +y 2 =2y ,所以x 2 +(y -1)2 =1,故答案为x 2 +(y -1)2 =1.
,它的直角坐标方程为x 2 +y 2 =2y ,所以x 2 +(y -1)2 =1,故答案为x 2 +(y -1)2 =1.
【考点 】 圆的极坐标方程.
59.(1)(x -1)2 +(y +2)2 =9,x -y -m =0;(2)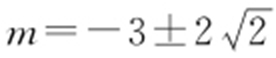 .
.
【解析 】 (1)消去参数t ,得到圆的普通方程为(x -1)2 +(y +2)2 =9,由 ,得
,得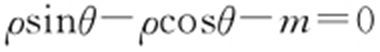 ,所以直线l 的直角坐标方程为y -x -m =0.
,所以直线l 的直角坐标方程为y -x -m =0.
(2)依题意,圆心C 到直线l 的距离等于2,即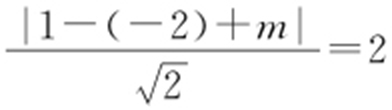 ,解得
,解得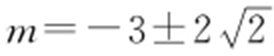 .
.
【考点 】 参数方程和普通方程的互化;极坐标和直角坐标方程的互化;点到直线的距离.
60.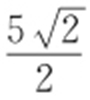 .
.
【解析 】 直线l 的极坐标方程为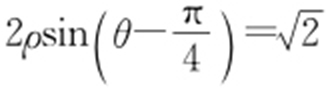 ,对应的直角坐标方程为y -x =1,点A 的极坐标为
,对应的直角坐标方程为y -x =1,点A 的极坐标为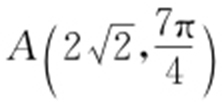 ,它的直角坐标为(2,-2).点A 到直线l 的距离为
,它的直角坐标为(2,-2).点A 到直线l 的距离为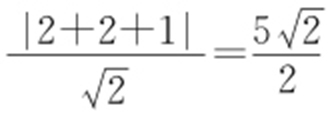 .
.
【考点 】 简单曲线的极坐标方程.
61.(1)x 2 +y 2 -2x =0;(2)18.
【解析 】 (1)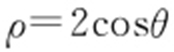 等价于
等价于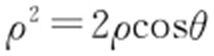 ,将
,将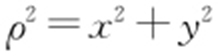 ,
, 代入上式即得曲线C 的直角坐标方程是x 2 +y 2 -2x =0.
代入上式即得曲线C 的直角坐标方程是x 2 +y 2 -2x =0.
(2)将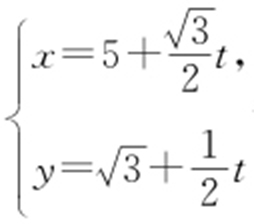 代入x 2 +y 2 -2x =0,得
代入x 2 +y 2 -2x =0,得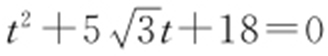 .设这个方程的两个实根分 别为t 1 ,t 2 ,则由参数t 的几何意义,知|MA |·|MB |=|t 1 t 2 |=18.
.设这个方程的两个实根分 别为t 1 ,t 2 ,则由参数t 的几何意义,知|MA |·|MB |=|t 1 t 2 |=18.
【考点 】 直线参数方程中t 的几何意义.
62.(2,π).
【解析 】 由直线l 的参数方程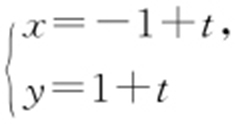 (t 为参数),得直线方程为x -y +2=0①;由
(t 为参数),得直线方程为x -y +2=0①;由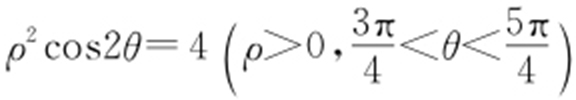 ,得
,得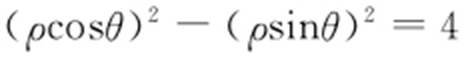 ,故x 2 -y 2 =4②.联立①,②:
,故x 2 -y 2 =4②.联立①,②: 易得交点坐标(-2,0),较易得交点的极坐标为(2,π).
易得交点坐标(-2,0),较易得交点的极坐标为(2,π).
【考点 】 参数方程的化简;直角坐标系与极坐标的转化.
63.(1)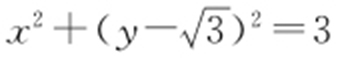 ;(2)(3,0).
;(2)(3,0).
【解析 】 (1)由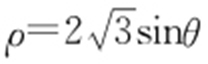 ,得
,得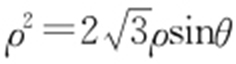 ,从而有
,从而有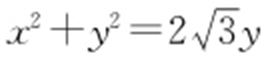 ,所以
,所以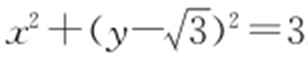 .
.
(2)设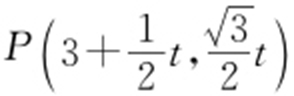 ,又
,又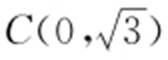 ,则
,则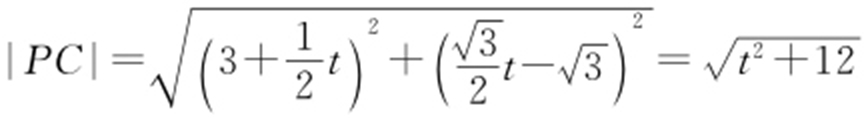 ,故当t =0时,|PC |取得最小值,此时P 点的坐标为(3,0).
,故当t =0时,|PC |取得最小值,此时P 点的坐标为(3,0).
【考点 】 坐标系与参数方程的转化;点与圆的位置关系.
64.(1)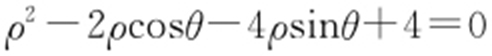 ;(2)
;(2)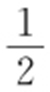 .
.
【解析 】 (1)因为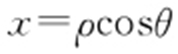 ,
, ,所以C 1 的极坐标方程为
,所以C 1 的极坐标方程为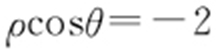 ,C 2 的极坐标方程为
,C 2 的极坐标方程为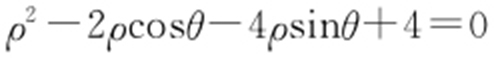 .
.
(2)将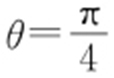 代入
代入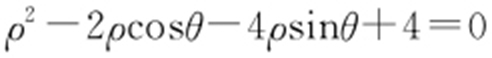 ,得
,得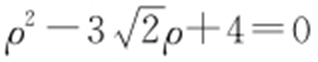 ,解得
,解得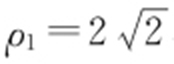 ,
,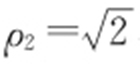 ,故
,故 ,即
,即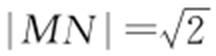 .由于C 2 的半径为1,所以△C 2 MN 的面积为
.由于C 2 的半径为1,所以△C 2 MN 的面积为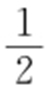 .
.
【考点 】 直线与圆的极坐标方程.
65.(1)(0,0),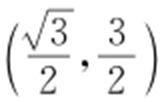 ;(2)4.
;(2)4.
【解析 】 (1)曲线C 2 的直角坐标方程为x 2 +y 2 -2y =0,曲线C 3 的直角坐标方程为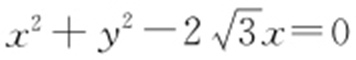 ,联立解得
,联立解得 或
或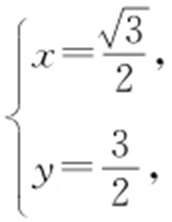 所以C 2 与C 3 交点的直角坐标为(0,0),
所以C 2 与C 3 交点的直角坐标为(0,0),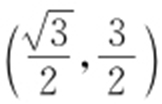 .
.
(2)曲线C 1 极坐标方程为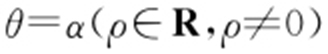 ,其中0≤α ≤π,因此点A 的极坐标为(2sinα ,α ),点B 的极坐标为
,其中0≤α ≤π,因此点A 的极坐标为(2sinα ,α ),点B 的极坐标为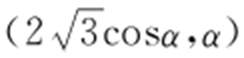 ,所以
,所以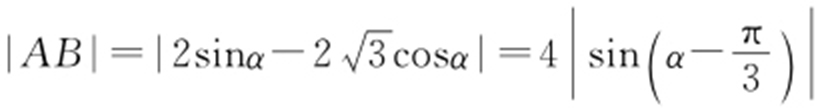 .当
.当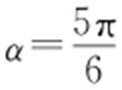 时,|AB |取得最大值,最大值为4.
时,|AB |取得最大值,最大值为4.
【考点 】 参数方程、直角坐标及极坐标方程的互化.
66.(2,-4).
【解析 】 曲线C 1 的直角坐标系方程为x +y =-2,曲线C 2 的直角坐标方程为y 2 =8x .联立方程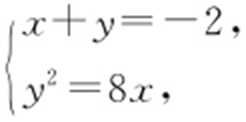 解得
解得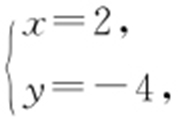 ,所以 C 1 与C 2 交点的直角坐标为(2,-4).
,所以 C 1 与C 2 交点的直角坐标为(2,-4).
【考点 】 简单曲线的极坐标方程.
67.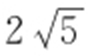 .
.
【解析 】 因为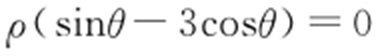 ,所以
,所以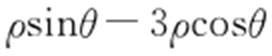 ,所以y -3x =0,即y =3x .由
,所以y -3x =0,即y =3x .由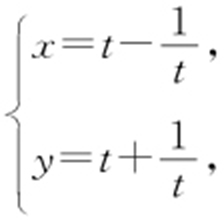 消去t 得y 2 -x 2 =4,联立方程组
消去t 得y 2 -x 2 =4,联立方程组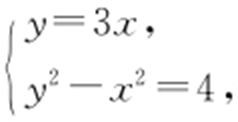 解得
解得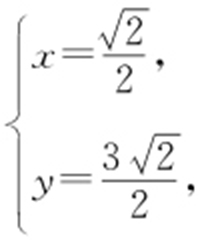 或
或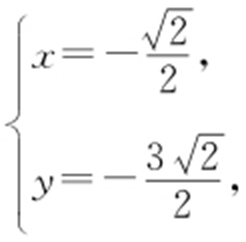 即
即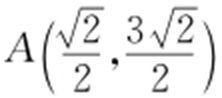 ,
,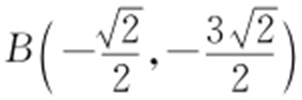 .
.
由两点间的距离公式,得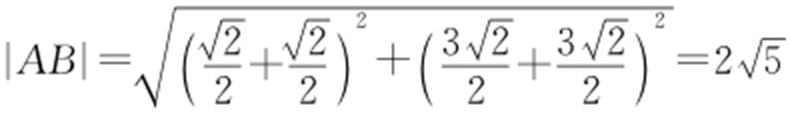 .
.
【考点 】 极坐标方程、参数方程与普通方程的转化;两点间的距离.
第9章 解析几何2016年真题必刷
直线与圆
1.C.
【解析 】 圆心坐标为(-1,0),由点到直线的距离公式可知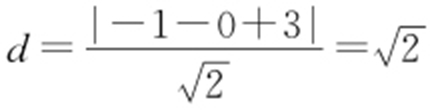 .故选:C.
.故选:C.
【考点 】 点到直线的距离.
2.4.
【解析 】 因为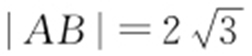 ,且圆的半径为
,且圆的半径为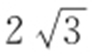 ,所以圆心(0,0)到直线
,所以圆心(0,0)到直线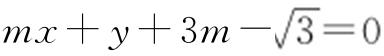 的距离为
的距离为 ,则由
,则由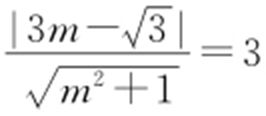 ,解得
,解得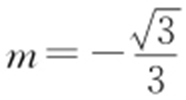 ,代入直线l 的方程,得
,代入直线l 的方程,得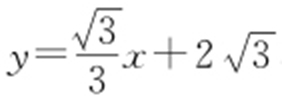 ,所以直线l 的倾斜角为30°,由平面几何知识知在梯形ABDC 中,
,所以直线l 的倾斜角为30°,由平面几何知识知在梯形ABDC 中,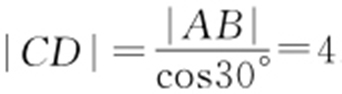 .
.
【考点 】 圆的弦长公式.
3.4.
【考点 】 直线与相交的弦长.
4.4π.
【解析 】 圆C :x 2 +y 2 -2ay -2=0,即C :x 2 +(y -a )2 =a 2 +2,圆心为C (0,a ),由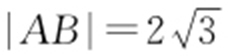 ,C 到直线y =x +2a 的距离为
,C 到直线y =x +2a 的距离为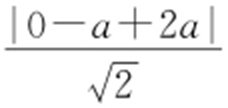 ,所以由
,所以由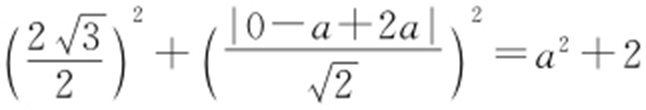 ,得a 2 =2,所以圆的面积为π(a 2 +2)=4π.
,得a 2 =2,所以圆的面积为π(a 2 +2)=4π.
【考点 】 圆的弦长公式.
5.A.
【解析 】 圆的方程可化为(x -1)2 +(y -4)2 =4,所以圆心坐标为(1,4),由点到直线的距离公式得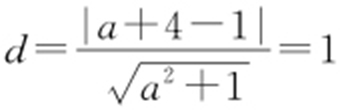 ,解得
,解得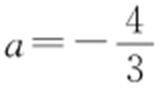 .故选:A.
.故选:A.
【考点 】 点到直线的距离.
6.B.
【解析 】 由x 2 +y 2 -2ay =0(a >0),得x 2 +(y -a )2 =a 2 (a >0),所以圆M 的圆心为(0,a ),半径为r 1 =a ,因为圆M 截直线x +y =0所得线段的长度是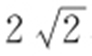 ,所以
,所以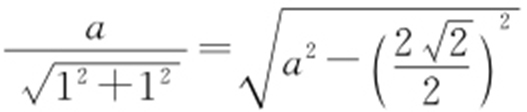 ,解得a =2.圆N 的圆心为(1,1),半径为r 2 =1,所以
,解得a =2.圆N 的圆心为(1,1),半径为r 2 =1,所以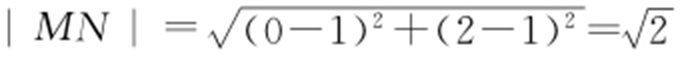 ,r 1 +r 2 =3,r 1 -r 2 =1,因为r 1 -r 2 <|MN |<r 1 +r 2 ,所以圆M 与圆N 相交.故选:B.
,r 1 +r 2 =3,r 1 -r 2 =1,因为r 1 -r 2 <|MN |<r 1 +r 2 ,所以圆M 与圆N 相交.故选:B.
【考点 】 圆的弦长公式;圆与圆的关系.
7.(x -2)2 +y 2 =9.
【解析 】 设C (a ,0)(a >0),则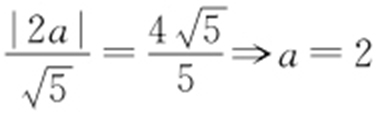 ,
,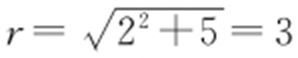 ,故圆C 的方程为(x -2)2 +y 2 =9.
,故圆C 的方程为(x -2)2 +y 2 =9.
【考点 】 点到直线的距离.
8.(-2,-4),r =5.
【考点 】 圆的一般方程.
9.(1)(x -6)2 +(y -1)2 =1;(2)2x -y +5=0或2x -y -15=0;
(3)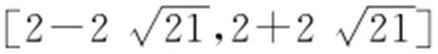 .
.
【解析 】 圆M 的标准方程为(x -6)2 +(y -7)2 =25,所以圆心M (6,7),半径为5.
(1)由圆心在直线x =6上,可设N (6,y 0 ).因为圆N 与x 轴相切,与圆M 外切,所以0<y 0 <7,于是设圆N 的半径为y 0 ,从而7-y 0 =5+y 0 ,解得y 0 =1.
因此,圆N 的标准方程为(x -6)2 +(y -1)2 =1.
(2)因为直线l ∥OA ,所以直线l 的斜率为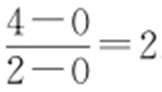 .
.
设直线l 的方程为y =2x +m ,即2x -y +m =0,则圆心M 到直线l 的距离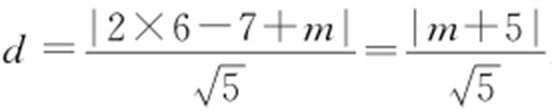 .因为
.因为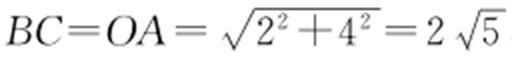 ,而
,而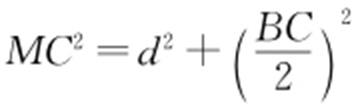 ,所以
,所以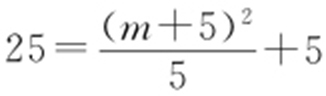 ,解得m =5或m =-15,故直线l 的方程为2x -y +5=0或2x -y -15=0.
,解得m =5或m =-15,故直线l 的方程为2x -y +5=0或2x -y -15=0.
(3)设P (x 1 ,y 1 ),Q (x 2 ,y 2 ).
因为A (2,4),T (t ,0),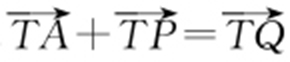 ,所以
,所以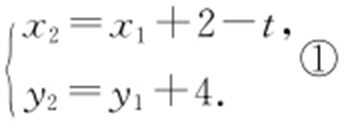
因为点Q 在圆M 上,所以(x 2 -6)2 +(y 2 -7)2 =25②.
将①代入②,得(x 1 -t -4)2 +(y 1 -3)2 =25.于是点P (x 1 ,y 1 )既在圆M 上,又在圆[x -(t +4)]2 +(y -3)2 =25上,从而圆(x -6)2 +(y -7)2 =25与圆[x -(t +4)]2 +(y -3)2 =25有公共点,所以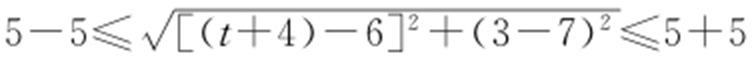 ,解得
,解得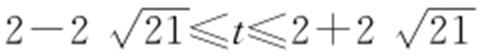 .
.
因此,实数t 的取值范围是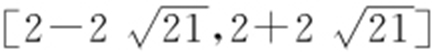 .
.
【考点 】 直线与圆的位置关系;点到直线的距离;圆与圆的位置关系.
10.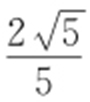 .
.
【考点 】 平行直线的距离公式.
11.C.
【考点 】 线性规划类型①.
12.C.
【考点 】 线性规划类型②.
13.216000.
【解析 】 设生产产品A 、产品B 分别为x ,y 件,利润之和为z 元,那么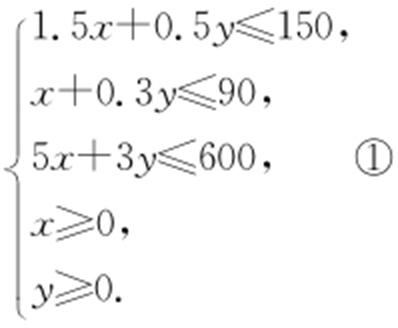
目标函数z =2100x +900y .
二元一次不等式组①等价于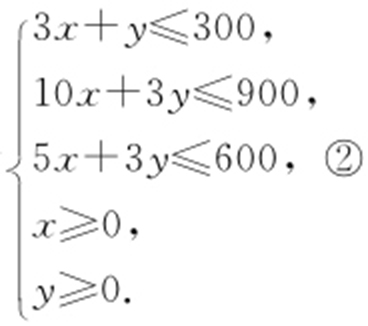
作出二元一次不等式组②表示的平面区域(如图),即可行域.
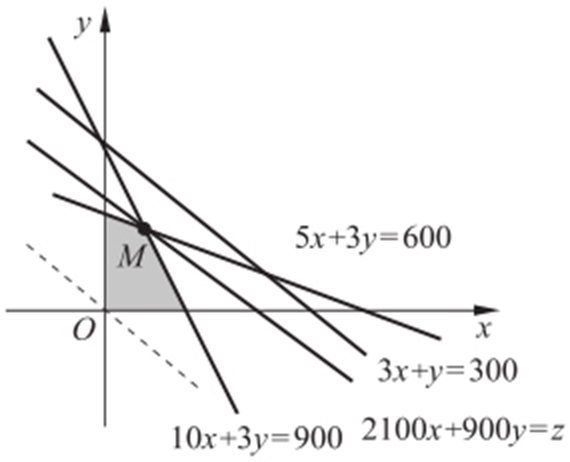
将z =2100x +900y 变形,得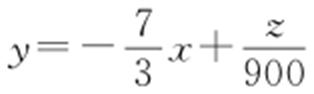 ,平行直线
,平行直线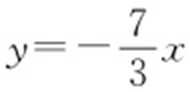 ,当直线
,当直线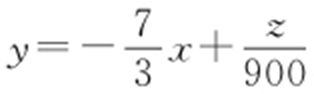 经过点M 时,z 取得最大值.解方程组
经过点M 时,z 取得最大值.解方程组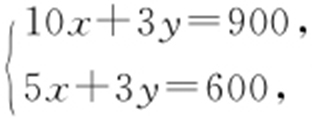 得M 的坐标为(60,100).所以当x =60,y =100时,z max =2100×60+900×100=216000.
得M 的坐标为(60,100).所以当x =60,y =100时,z max =2100×60+900×100=216000.
【考点 】 线性规划的实际应用.
14.-5.
【解析 】 由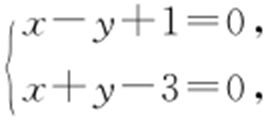 得
得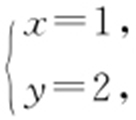 点A (1,2).由
点A (1,2).由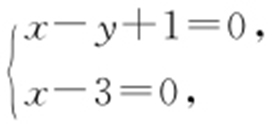 得
得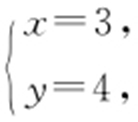 点B (3,4).由
点B (3,4).由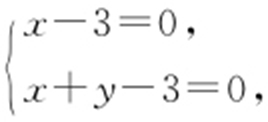 得
得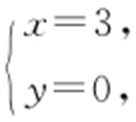 点C (3,0).分别将A ,B ,C 代入z =x -2y ,得zA =-3,zB =-5,zC =3,所以z =x -2y 的最小值为-5.
点C (3,0).分别将A ,B ,C 代入z =x -2y ,得zA =-3,zB =-5,zC =3,所以z =x -2y 的最小值为-5.
【考点 】 线性规划的形式①.
15.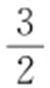 .
.
【考点 】 线性规划的形式①.
16.-10.
【解析 】 可行域为一个△ABC 及其内部,其中A (1,0),B (-1,-1),C (1,3),直线z =2x +3y -5过点B 时取最小值-10.
【考点 】 线性规划的形式①.
17.C.
【考点 】 线性规划的形式③.
18.-2.
【考点 】 线性规划的形式①.
19.B.
【考点 】 线性规划的形式①.
20.B.
【考点 】 平行线间的距离.

21. .
.
【解析 】 在平面直角坐标系中画出可行域如图,x 2 +y 2 为可行域内的点到原点距离的平方.
可以看出图中A 点距离原点最近,此时距离为原点A 到直线2x +y -2=0的距离,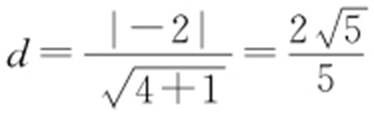 ,则
,则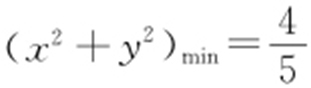 ,图中B 点距离原点最远,B 点为x -2y +4=0与3x -y -3=0交点,则B (2,3),则(x 2 +y 2 )max =13.
,图中B 点距离原点最远,B 点为x -2y +4=0与3x -y -3=0交点,则B (2,3),则(x 2 +y 2 )max =13.
【考点 】 线性规划类型③.
圆锥曲线
22.2.
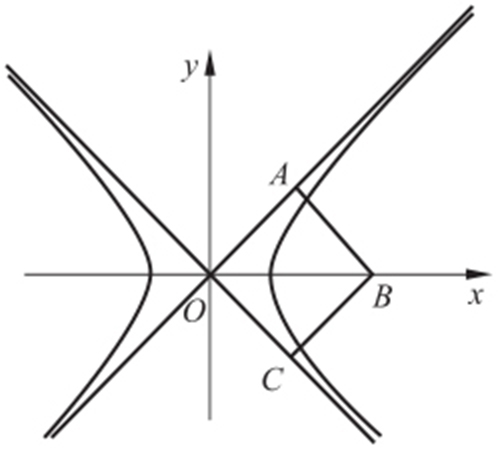
【解析 】 双曲线的渐近线为正方形OABC 的边OA ,OC 所在的直线,所以渐近线互相垂直,则双曲线为等轴双曲线,即渐近线方程为y =±x ,即a =b .
因为正方形OABC 的边长为2,所以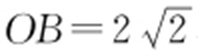 ,即
,即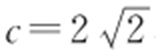 ,则a 2 +b 2 =c 2 =8,即2a 2 =8,则a 2 =4,a =2.
,则a 2 +b 2 =c 2 =8,即2a 2 =8,则a 2 =4,a =2.
【考点 】 双曲线的几何性质.
23.a =1,b =2.
【解析 】 依题意有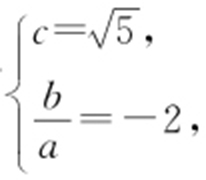 结合c 2 =a 2 +b 2 ,解得a =1,b =2.
结合c 2 =a 2 +b 2 ,解得a =1,b =2.
【考点 】 双曲线的渐近线方程.
24.A.
【解析 】 由题意知,双曲线的焦点在x 轴上,所以m 2 +n +3m 2 -n =4,解得m 2 =1.因为方程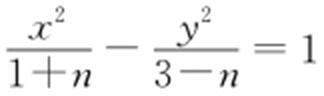 表示双曲线,所以
表示双曲线,所以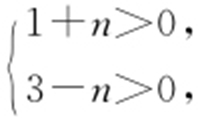 解得
解得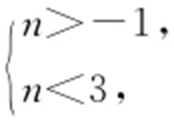 ,所以n 的取值范围是 (-1,3).故选:A.
,所以n 的取值范围是 (-1,3).故选:A.
【考点 】 双曲线的一般方程.
25.B.
【解析 】 设抛物线方程为y 2 =2px ,AB ,DE 交x 轴于C ,F 点,则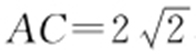 ,即A 点纵坐标为
,即A 点纵坐标为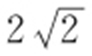 ,则A 点横坐标为
,则A 点横坐标为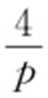 ,即
,即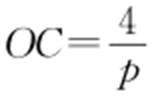 ,由勾股定理知DF 2 +OF 2 =DO 2 =r 2 ,AC 2 +OC 2 =AO 2 =r 2 ,即
,由勾股定理知DF 2 +OF 2 =DO 2 =r 2 ,AC 2 +OC 2 =AO 2 =r 2 ,即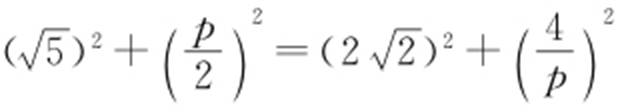 ,解得p =4,即C 的焦点到准线的距离为4.故选:B.
,解得p =4,即C 的焦点到准线的距离为4.故选:B.
【考点 】 抛物线的准线.
26.B.
【解析 】 由题意知在椭圆中,OF =c ,OB =b ,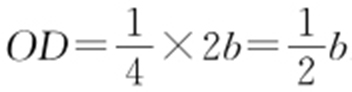 .
.
在Rt△OFB 中,|OF |×|OB |=|BF |×|OD |,且a 2 =b 2 +c 2 ,代入解得a 2 =4c 2 ,所以得离心率为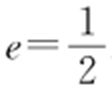 .故选:B.
.故选:B.
【考点 】 椭圆的离心率.
27.A.
【解析 】 因为MF 1 垂直于x 轴,所以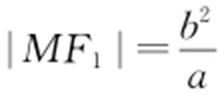 ,
,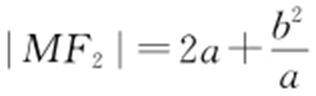 ,因为
,因为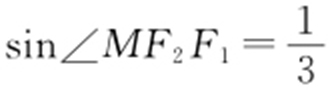 ,即
,即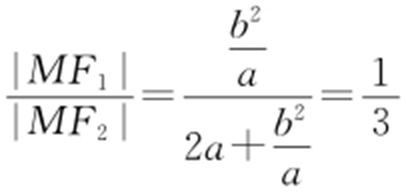 ,化简得b =a ,故双曲线离心率
,化简得b =a ,故双曲线离心率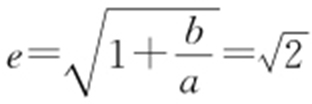 .故选:A.
.故选:A.
【考点 】 双曲线的通径长;双曲线的离心率.
28.D.
【考点 】 抛物线的概念和对称性.
29.A.
【解析 】 由题意设直线l 的方程为y =k (x +a ),分别令x =-c 与x =0,得|FM |=k (a -c ),|OE |=ka ,由△OBE ∽△CBM ,得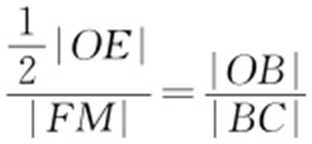 ,即
,即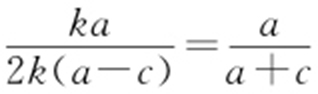 ,整理得
,整理得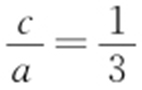 ,所以椭圆离心率为
,所以椭圆离心率为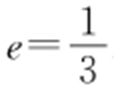 .故选:A.
.故选:A.
【考点 】 椭圆的离心率.
30.2.
【解析 】 易得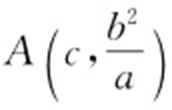 ,
,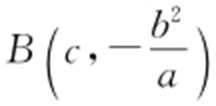 ,所以
,所以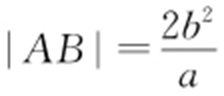 ,|BC |=2c .由2|AB |=3|BC |,c 2 =a 2 +b 2 ,得离心率e =2或
,|BC |=2c .由2|AB |=3|BC |,c 2 =a 2 +b 2 ,得离心率e =2或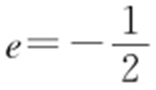 (舍去),所以离心率为2.
(舍去),所以离心率为2.
【考点 】 双曲线的离心率.
31.D.
【解析 】 由题意,y 2 =4x 的焦点坐标为(1,0).故选:D.
【考点 】 抛物线的方程.
32.D.
【解析 】 根据对称性,不妨设A 在第一象限,A (x ,y ),所以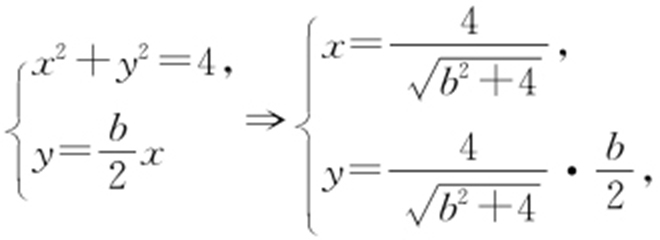 所以
所以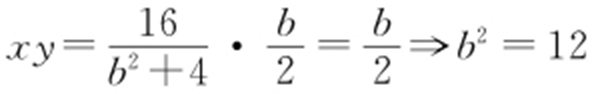 ,故双曲线的方程为
,故双曲线的方程为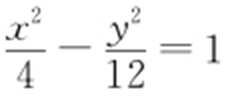 .故选:D.
.故选:D.
【考点 】 双曲线的方程.
33.A.
【解析 】 由题意得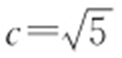 ,
,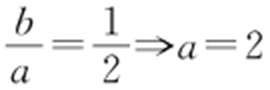 ,
,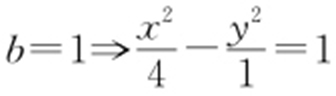 .故选:A.
.故选:A.
【考点 】 双曲线的方程.
34.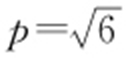 .
.
【解析 】 抛物线的普通方程为y 2 =2px ,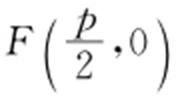 ,
,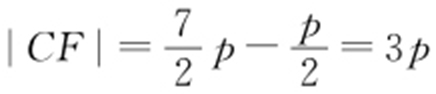 ,又|CF |=2|AF |,则
,又|CF |=2|AF |,则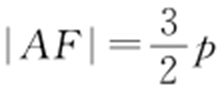 ,由抛物线的定义得
,由抛物线的定义得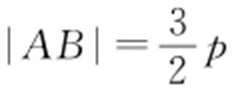 ,所以xA =p ,则
,所以xA =p ,则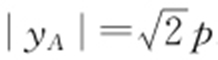 .由CF ∥AB 得
.由CF ∥AB 得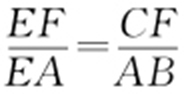 ,即
,即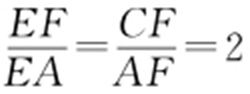 ,所以
,所以 ,
,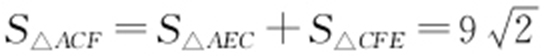 ,所以
,所以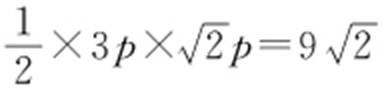 ,
,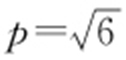 .
.
【考点 】 抛物线的方程.
35.A.
【解析 】 由题意知m 2 -1=n 2 +1,即m 2 =n 2 +2,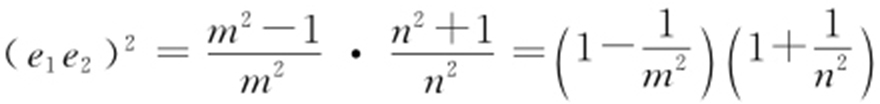 ,代入m 2 =n 2 +2,得m >n ,(e 1 e 2 )2 >1.故选:A.
,代入m 2 =n 2 +2,得m >n ,(e 1 e 2 )2 >1.故选:A.
【考点 】 椭圆与双曲线的离心率.
36.9.
【解析 】 xM +1=10⇒xM =9.
【考点 】 抛物线的焦半径.
37.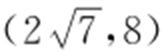 .
.
【解析 】 由已知a =1,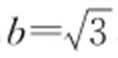 ,c =2,则
,c =2,则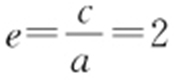 ,设P (x ,y )是双曲线上任一点,由对称性不妨设P 在右支上,则1<x <2,|PF 1 |=2x +1,|PF 2 |=2x -1,∠F 1 PF 2 为锐角,则|PF 1 |2 +|PF 2 |2 >|F 1 F 2 |2 ,即(2x +1)2 +(2x -1)2 >42 ,解得
,设P (x ,y )是双曲线上任一点,由对称性不妨设P 在右支上,则1<x <2,|PF 1 |=2x +1,|PF 2 |=2x -1,∠F 1 PF 2 为锐角,则|PF 1 |2 +|PF 2 |2 >|F 1 F 2 |2 ,即(2x +1)2 +(2x -1)2 >42 ,解得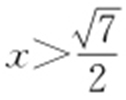 ,所以
,所以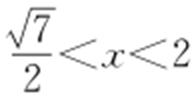 ,
, .
.
【考点 】 双曲线的定义.
38.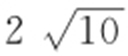 .
.
【解析 】 因为a 2 =7,b 2 =3,所以c 2 =a 2 +b 2 =7+3=10,则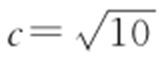 ,即
,即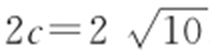 .
.
【考点 】 双曲线的方程.
39.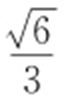 .
.
【解析 】 由题意得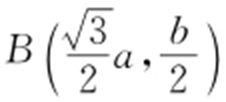 ,
,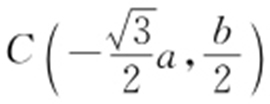 ,因此
,因此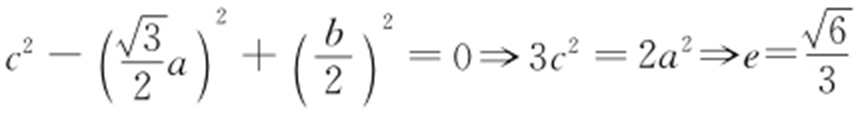 .
.
【考点 】 椭圆的离心率.
40.(1)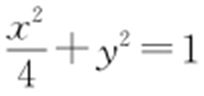 ;(2)定值为4.
;(2)定值为4.
【解析 】 (1)由题意可得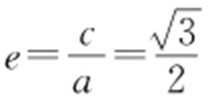 ,又△OAB 的面积为1,可得
,又△OAB 的面积为1,可得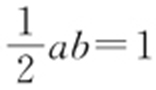 ,且a 2 -b 2 =c 2 ,解得a =2,b =1,
,且a 2 -b 2 =c 2 ,解得a =2,b =1,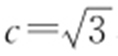 ,可得椭圆C 的方程为
,可得椭圆C 的方程为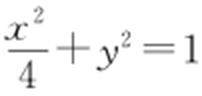 .
.
(2)证法1:设椭圆上点P (x 0 ,y 0 ),可得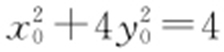 .
.
直线PA :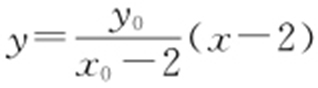 ,令x =0,可得
,令x =0,可得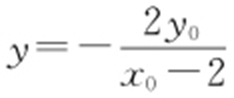 ,则
,则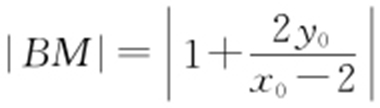 ;
;
直线PB : ,令y =0,可得
,令y =0,可得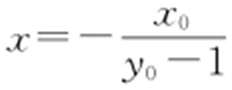 ,则
,则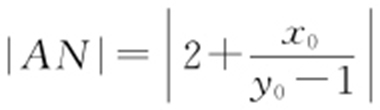 .
.
证法2:设P (2cosθ ,sinθ ),(0≤θ <2π).
直线PA :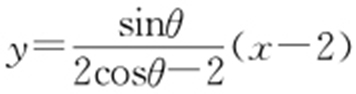 ,令x =0,可得
,令x =0,可得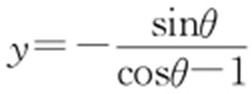 ,则
,则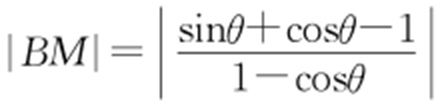 ;
;
直线PB :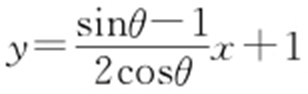 ,令y =0,可得
,令y =0,可得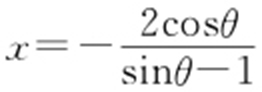 ,则
,则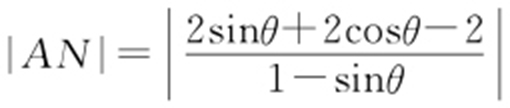 .
.
【考点 】 直线与椭圆的位置关系.
41.(1)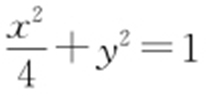 ,
, ;(2)定值为2.
;(2)定值为2.
【解析 】 (1)由题意得,a =2,b =1.所以椭圆C 的方程为 .又
.又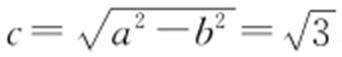 ,所以离心率
,所以离心率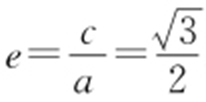 .
.
(2)设P (x 0 ,y 0 )(x 0 <0,y 0 <0),则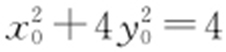 .又A (2,0),B (0,1),所以直线PA 的方程为
.又A (2,0),B (0,1),所以直线PA 的方程为 .
.
令x =0,得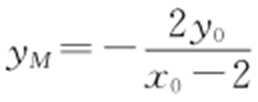 ,从而
,从而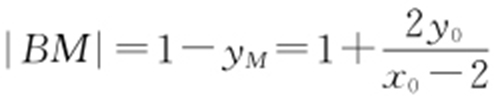 .
.
直线PB 的方程为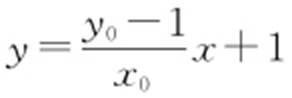 ,令y =0,得
,令y =0,得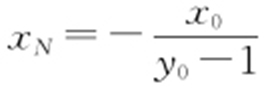 ,从而
,从而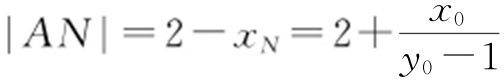 .所以四边形ABNM 的面积
.所以四边形ABNM 的面积
从而四边形ABNM 的面积为定值.
【考点 】 椭圆的离心率;对角线垂直的四边形的面积.
42.(1)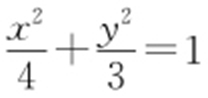 (y ≠0);(2)
(y ≠0);(2) .
.
【解析 】 (1)因为|AD |=|AC |,EB //AC ,故∠EBD =∠ACD =∠ADC ,所以|EB |=|ED |,故|EA |+|EB |=|EA |+|ED |=|AD |.
又圆A 的标准方程为(x +1)2 +y 2 =16,从而|AD |=4,所以|EA |+|EB |=4.
由题设得A (-1,0),B (1,0),|AB |=2,由椭圆定义可得点E 的轨迹方程为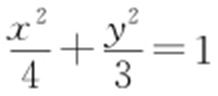 (y ≠0).
(y ≠0).
(2)当l 与x 轴不垂直时,设l 的方程为y =k (x -1)(k ≠0),M (x 1 ,y 1 ),N (x 2 ,y 2 ).
由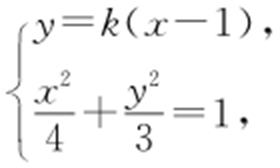 得(4k 2 +3)x 2 -8k 2 x +4k 2 -12=0,则
得(4k 2 +3)x 2 -8k 2 x +4k 2 -12=0,则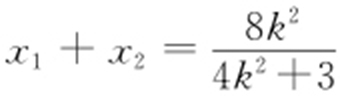 ,
,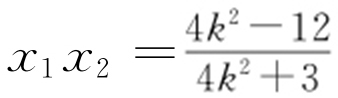 ,所以
,所以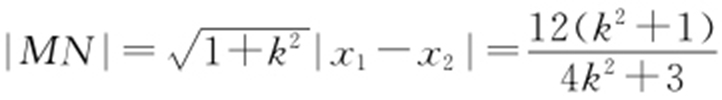 .
.
过点B (1,0)且与l 垂直的直线m :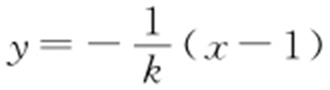 ,A 到m 的距离为
,A 到m 的距离为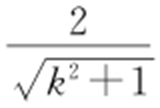 ,所以
,所以 .故四边形MPNQ 的面积
.故四边形MPNQ 的面积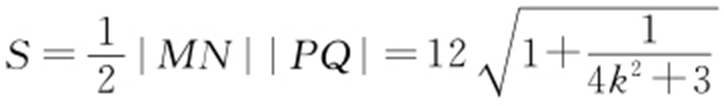 .
.
可得当l 与x 轴不垂直时,四边形MPNQ 面积的取值范围为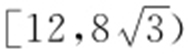 .
.
当l 与x 轴垂直时,其方程为x =1,|MN |=3,|PQ |=8,四边形MPNQ 的面积为12.
综上,四边形MPNQ 面积的取值范围为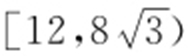 .
.
【考点 】 椭圆的离心率;对角线垂直的四边形的面积.
43.(1)2;(2)没有.
【解析 】 (1)由已知得M (0,t ),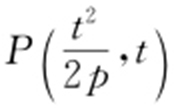 .
.
又N 为M 关于点P 的对称点,故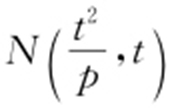 ,ON 的方程为
,ON 的方程为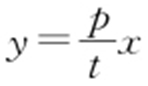 ,代入y 2 =2px ,整理得px 2 -2t 2 x =0,解得x 1 =0,
,代入y 2 =2px ,整理得px 2 -2t 2 x =0,解得x 1 =0, ,因此
,因此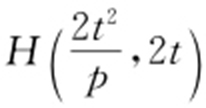 .所以N 为OH 的中点,即
.所以N 为OH 的中点,即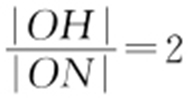 .
.
(2)直线MH 与C 除H 以外没有其他公共点.理由如下:
直线MH 的方程为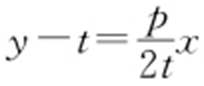 ,即
,即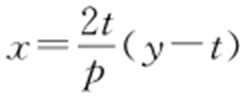 .代入y 2 =2px ,得y 2 -4ty +4t 2 =0,解得y 1 =y 2 =2t ,即直线MH 与C 只有一个公共点,所以除H 以外直线MH 与C 没有其他公共点.
.代入y 2 =2px ,得y 2 -4ty +4t 2 =0,解得y 1 =y 2 =2t ,即直线MH 与C 只有一个公共点,所以除H 以外直线MH 与C 没有其他公共点.
【考点 】 抛物线的概念;直线与抛物线的交点问题.
44.(1)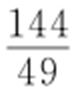 ;(2)
;(2)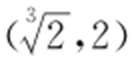 .
.
【解析 】 (1)设M (x 1 ,y 1 ),则由题意知y 1 >0,当t =4时,E 的方程为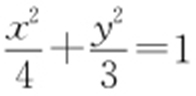 ,A (-2,0).
,A (-2,0).
由已知及椭圆的对称性知,直线AM 的倾斜角为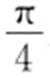 .因此直线AM 的方程为y =x +2.
.因此直线AM 的方程为y =x +2.
将x =y -2代入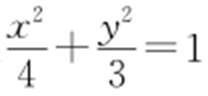 ,得7y 2 -12y =0,解得y =0或
,得7y 2 -12y =0,解得y =0或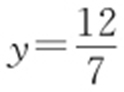 ,所以
,所以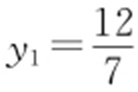 .
.
因此 .
.
(2)由题意t >3,k >0,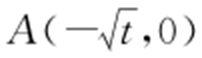 .
.
将直线AM 的方程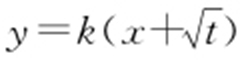 代入
代入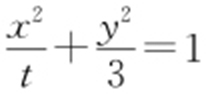 ,得
,得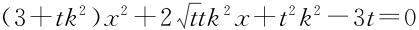 .
.
由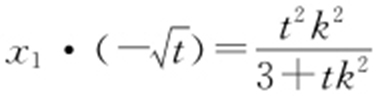 ,得
,得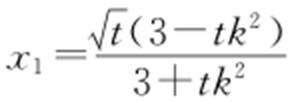 ,故
,故 .
.
由题设,直线AN 的方程为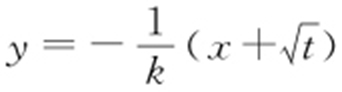 ,故同理可得
,故同理可得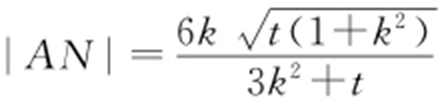 ,由2|AM |=|AN |,得
,由2|AM |=|AN |,得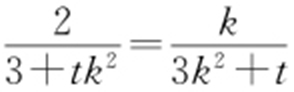 ,即(k 3 -2)t =3k (2k -1).
,即(k 3 -2)t =3k (2k -1).
当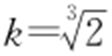 时上式不成立,因此
时上式不成立,因此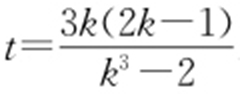 .t >3等价于
.t >3等价于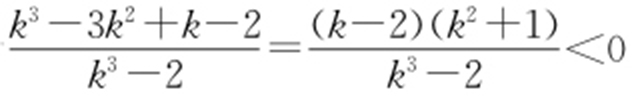 ,即
,即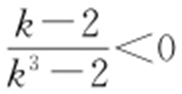 .由此得
.由此得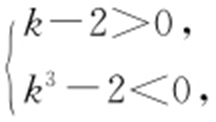 或
或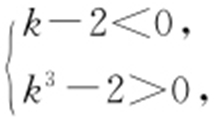 解得
解得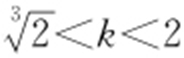 .因此k 的取值范围是
.因此k 的取值范围是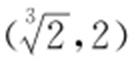 .
.
【考点 】 坐标化值坐标比问题.
45.(1)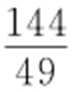 ;(2)详见解析.
;(2)详见解析.
【解析 】 (1)设M (x 1 ,y 1 ),则由题意知y 1 >0.
由已知及椭圆的对称性知,直线AM 的倾斜角为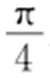 .又A (-2,0),因此直线AM 的方程为y =x +2.将x =y -2代入
.又A (-2,0),因此直线AM 的方程为y =x +2.将x =y -2代入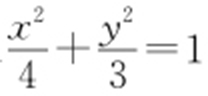 ,得7y 2 -12y =0,解得y =0(舍去)或
,得7y 2 -12y =0,解得y =0(舍去)或 .
.
因此△AMN 的面积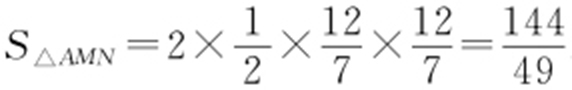 .
.
(2)将直线AM 的方程y =k (x +2)(k >0)代入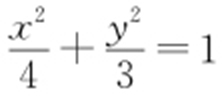 ,得(3+4k 2 )x 2 +16k 2 x +16k 2 -12=0.
,得(3+4k 2 )x 2 +16k 2 x +16k 2 -12=0.
由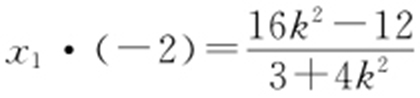 ,得
,得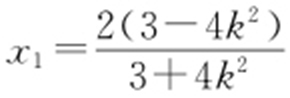 ,故
,故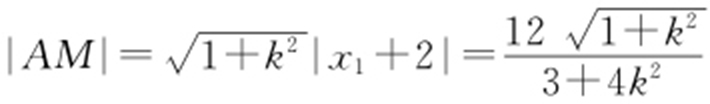 .
.
由题设,直线AN 的方程为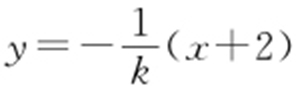 ,故同理可得
,故同理可得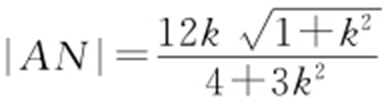 .
.
由2|AM |=|AN |得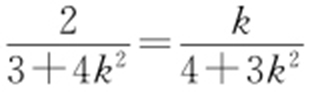 ,即4k 3 -6k 2 +3k -8=0.
,即4k 3 -6k 2 +3k -8=0.
设f (t )=4t 3 -6t 2 +3t -8,则k 是f (t )的零点,f′ (t )=12t 2 -12t +3=3(2t -1)2 ≥0,所以f (t )在(0,+∞)单调递增,又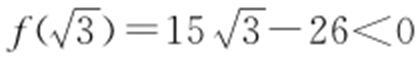 ,f (2)=6>0,因此f (t )在(0,+∞)有唯一的零点,且零点k 在
,f (2)=6>0,因此f (t )在(0,+∞)有唯一的零点,且零点k 在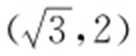 内,所以
内,所以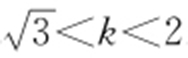 .
.
【考点 】 椭圆的性质;直线与椭圆的位置关系.
46.(1)略;(2)y 2 =x -1.
【解析 】 由题设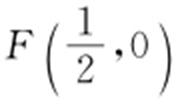 .设l 1 :y =a ,l 2 :y =b ,则ab ≠0,且
.设l 1 :y =a ,l 2 :y =b ,则ab ≠0,且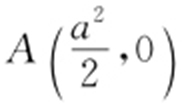 ,
,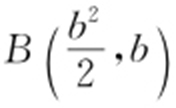 ,
,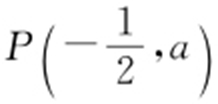 ,
, ,
,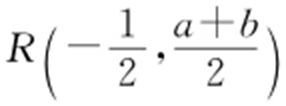 .
.
记过A ,B 两点的直线为l ,则l 的方程为2x -(a +b )y +ab =0.
(1)由于F 在线段AB 上,故1+ab =0.
记AR 的斜率为k 1 ,FQ 的斜率为k 2 ,则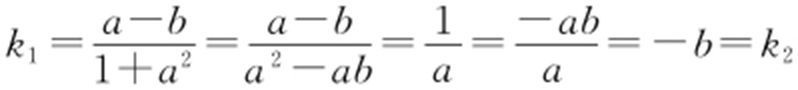 ,所以AR ∥FQ .
,所以AR ∥FQ .
(2)设l 与x 轴的交点为D (x 1 ,0),则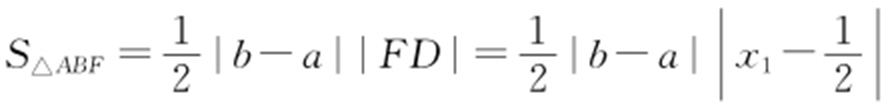 ,
,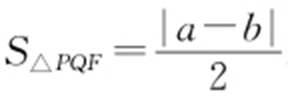 .
.
由题设可得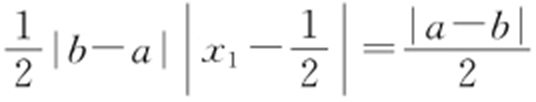 ,所以x 1 =0(舍去),x 2 =1.
,所以x 1 =0(舍去),x 2 =1.
设满足条件的AB 的中点为E (x ,y ).
当AB 与x 轴不垂直时,由kAB =kDE 可得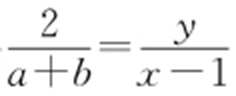 (x ≠1),而
(x ≠1),而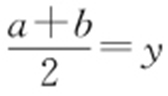 ,所以y 2 =x -1(x ≠1).
,所以y 2 =x -1(x ≠1).
当AB 与x 轴垂直时,E 与D 重合.所以,所求轨迹方程为y 2 =x -1.
【考点 】 相关关系法求轨迹方程.
47.(1)x 2 +4y 2 =1;(2)①略,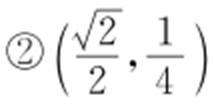 .
.
【解析 】 (1)由题意知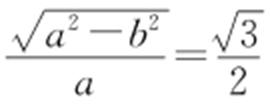 ,解得a =2b .因为抛物线E 的焦点为
,解得a =2b .因为抛物线E 的焦点为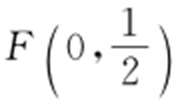 ,所以a =1,
,所以a =1,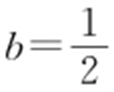 ,所以椭圆的方程为x 2 +4y 2 =1.
,所以椭圆的方程为x 2 +4y 2 =1.
(2)①设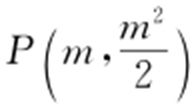 (m >0),由x 2 =2y 可得y′ =x ,所以直线l 的斜率为m ,其直线方程为
(m >0),由x 2 =2y 可得y′ =x ,所以直线l 的斜率为m ,其直线方程为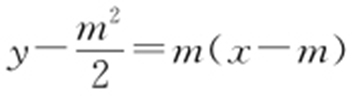 ,即
,即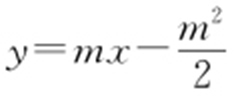 .
.
设A (x 1 ,y 1 ),B (x 2 ,y 2 ),D (x 0 ,y 0 ),联立方程组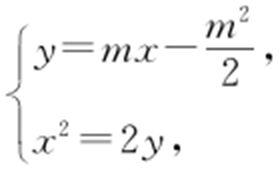 消去y 并整理可得(4m 2 +1)x 2 -4m 3 x +m 4 -1=0,故由其判别式Δ >0,可得
消去y 并整理可得(4m 2 +1)x 2 -4m 3 x +m 4 -1=0,故由其判别式Δ >0,可得 且
且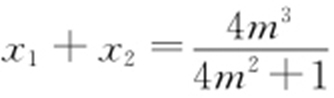 ,故
,故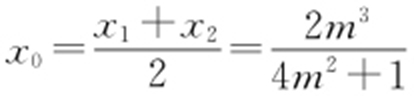 ,代入
,代入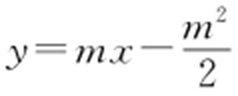 可得
可得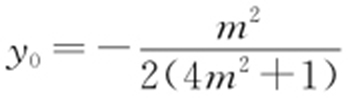 ,因为
,因为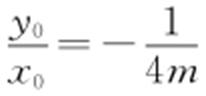 ,所以直线OD 的方程为
,所以直线OD 的方程为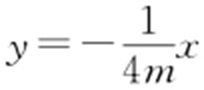 .
.
联立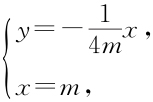 可得点M 的纵坐标为
可得点M 的纵坐标为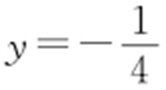 ,即点M 在定直线
,即点M 在定直线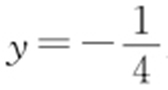 上.
上.
②由①知直线l 的方程为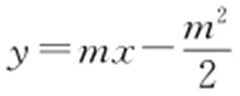 ,令x =0,得
,令x =0,得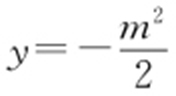 ,所以
,所以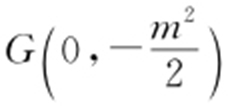 .
.
又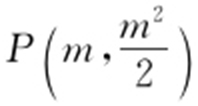 ,
,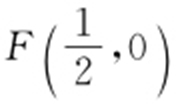 ,
,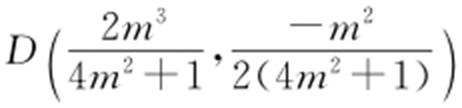 ,所以
,所以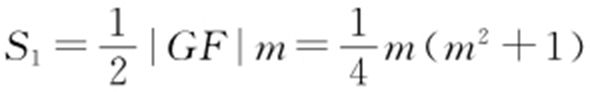 ,
,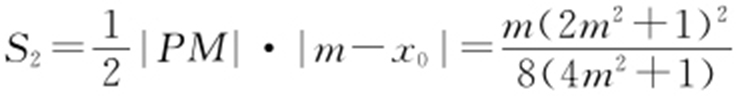 ,所以
,所以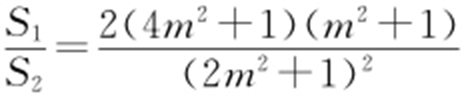 ,令t =2m 2 +1,则
,令t =2m 2 +1,则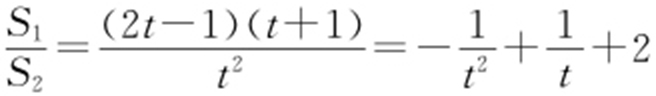 ,因此当
,因此当 (即t =2)时,
(即t =2)时,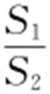 最大,其最大值为
最大,其最大值为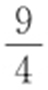 ,此时
,此时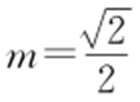 满足Δ >0,所以点P 的坐标为
满足Δ >0,所以点P 的坐标为 ,因此
,因此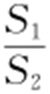 的最大值为
的最大值为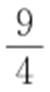 ,此时点P 的坐标为
,此时点P 的坐标为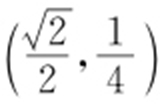 .
.
【考点 】 直线与椭圆相交.
48.(1)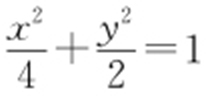 ;(2)①定值为-3,②
;(2)①定值为-3,② .
.
【解析 】 (1)设椭圆的半焦距为c ,由题意知2a =4,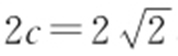 ,所以a =2,
,所以a =2,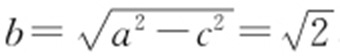 ,所以椭圆C 的方程为
,所以椭圆C 的方程为 .
.
(2)①设P (x 0 ,y 0 )(x 0 >0,y 0 >0),由M (0,m ),可得P (x 0 ,2m ),Q (x 0 ,-2m ).所以直线PM 的斜率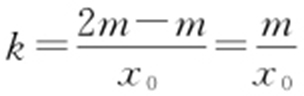 ,直线QM 的斜率
,直线QM 的斜率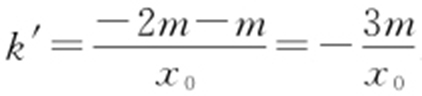 .此时
.此时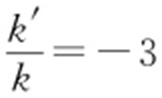 ,所以
,所以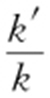 为定值-3.
为定值-3.
②设A (x 1 ,y 1 ),B (x 2 ,y x 2 ),直线PA 的方程为y =kx +m ,直线QB 的方程为y =-3kx +m .联立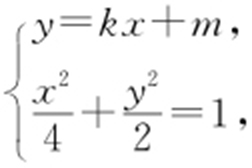 整理得(2k 2 +1)x 2 +4mkx +2m 2 -4=0.
整理得(2k 2 +1)x 2 +4mkx +2m 2 -4=0.
由 ,可得
,可得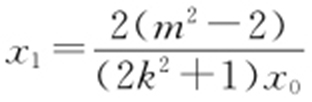 ,所以
,所以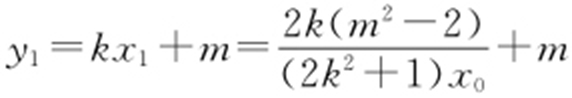 .
.
同理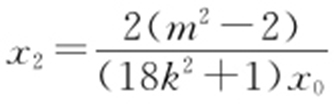 ,
, ,
,
所以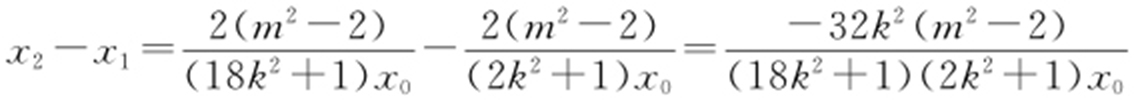 ,
,
,
所以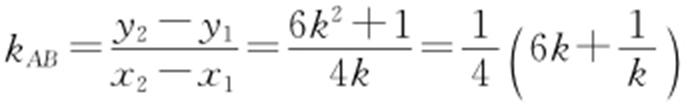 .
.
由m >0,x 0 >0,可知k >0,所以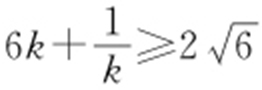 ,等号当且仅当
,等号当且仅当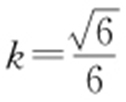 时取得.
时取得.
此时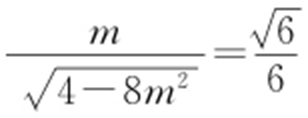 ,即
,即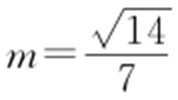 时,符合题意.
时,符合题意.
所以直线AB 的斜率的最小值为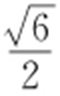 .
.
【考点 】 直线与椭圆相交.
49.(1)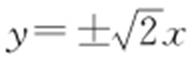 ;(2)l 的斜率为
;(2)l 的斜率为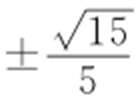 .
.
【解析 】 (1)设A (x A ,y A ).
由题意,F 2 (c ,0),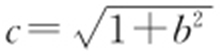 ,
,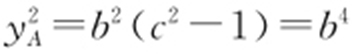 ,因为△F 1 AB 是等边三角形,所以
,因为△F 1 AB 是等边三角形,所以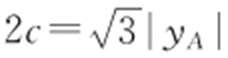 ,即4(1+b 2 )=3b 4 ,解得b 2 =2.故双曲线的渐近线方程为
,即4(1+b 2 )=3b 4 ,解得b 2 =2.故双曲线的渐近线方程为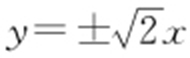 .
.
(2)由已知,F 2 (2,0).
设A (x 1 ,y 1 ),B (x 2 ,y 2 ),直线l :y =k (x -2).
由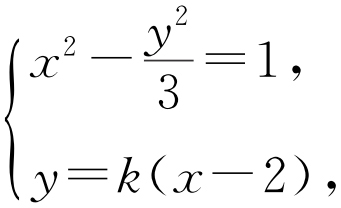 得(k 2 -3)x 2 -4k 2 x +4k 2 +3=0.
得(k 2 -3)x 2 -4k 2 x +4k 2 +3=0.
因为l 与双曲线交于两点,所以k 2 -3≠0,且Δ =36(1+k 2 )>0.
由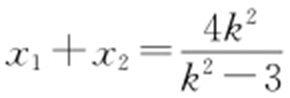 ,
,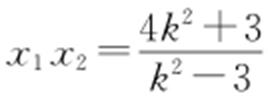 ,得
,得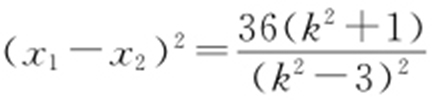 ,
,
故 ,解得
,解得 ,故l 的斜率为
,故l 的斜率为 .
.
【考点 】 向量在双曲线中的应用.
50.(1) ,(2,1);(2)
,(2,1);(2) .
.
【解析 】 (1)由已知,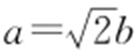 ,则椭圆E 的方程为
,则椭圆E 的方程为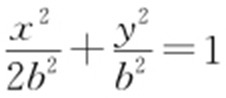 .由方程组
.由方程组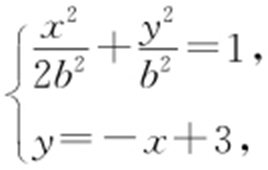 得3x 2 -12x +(18-2b 2 )=0①.
得3x 2 -12x +(18-2b 2 )=0①.
方程①的判别式为Δ =24(b 2 -3),由Δ =0,得b 2 =3,此方程①的解为x =2,所以椭圆E 的方程为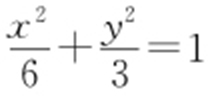 .点T 坐标为(2,1).
.点T 坐标为(2,1).
(2)由已知可设直线l′ 的方程为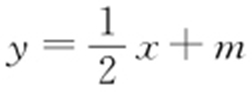 (m ≠0),由方程组
(m ≠0),由方程组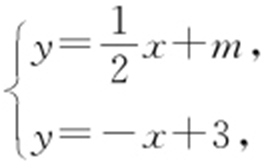 可得
可得  所以P 点坐标为
所以P 点坐标为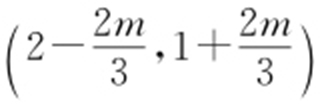 ,
,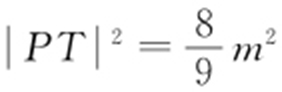 .设点A ,B 的坐标分别为A (x 1 ,y 1 ),B (x 2 ,y 2 ).由方程组
.设点A ,B 的坐标分别为A (x 1 ,y 1 ),B (x 2 ,y 2 ).由方程组 可得3x 2 +4mx +(4m 2 -12)=0②.
可得3x 2 +4mx +(4m 2 -12)=0②.
方程②的判别式为Δ =16(9-2m 2 ),由Δ >0,解得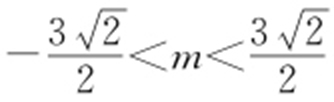 .
.
由②得 ,
,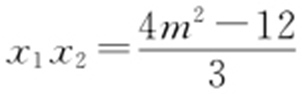 .
.
所以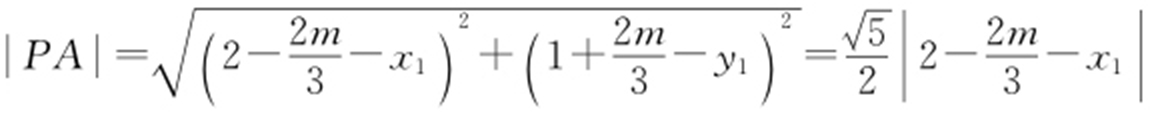 .
.
同理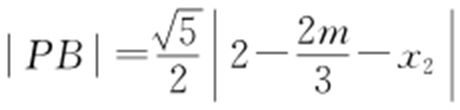 ,所以
,所以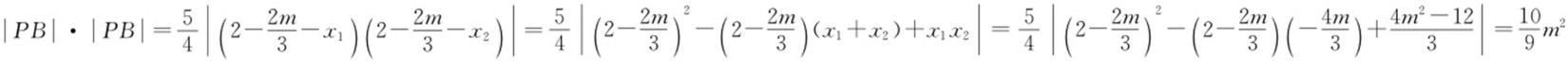 .故存在常数
.故存在常数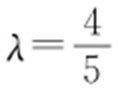 ,使得|PT |2 =λ |PA |·|PB |.
,使得|PT |2 =λ |PA |·|PB |.
【考点 】 直线与椭圆的相交问题.
51.(1) ;(2)略.
;(2)略.
【解析 】 (1)由已知,a =2b .又椭圆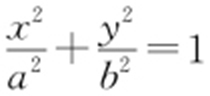 (a >b >0)过点
(a >b >0)过点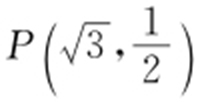 ,故
,故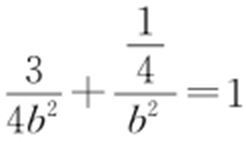 ,解得b 2 =1.所以椭圆E 的方程是
,解得b 2 =1.所以椭圆E 的方程是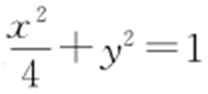 .
.
(2)设直线l 的方程为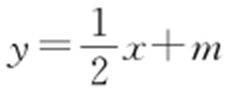 (m ≠0),A (x 1 ,y 1 ),B (x 2 ,y 2 ),由方程组
(m ≠0),A (x 1 ,y 1 ),B (x 2 ,y 2 ),由方程组 得x 2 +2mx +2m 2 -2=0①,方程①的判别式为Δ =4(2-m 2 ),由Δ >0,即2-m 2 >0,解得
得x 2 +2mx +2m 2 -2=0①,方程①的判别式为Δ =4(2-m 2 ),由Δ >0,即2-m 2 >0,解得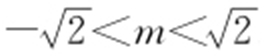 .
.
由①得x 1 +x 2 =-2m ,x 1 x 2 =2m 2 -2.所以M 点坐标为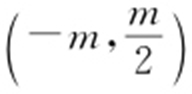 ,直线OM 方程为
,直线OM 方程为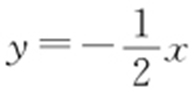 ,由方程组
,由方程组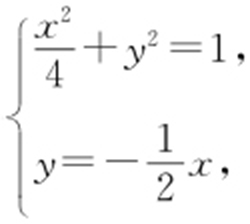 得
得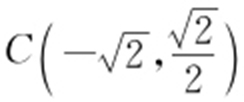 ,
,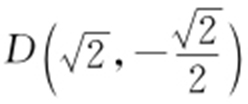 .所以
.所以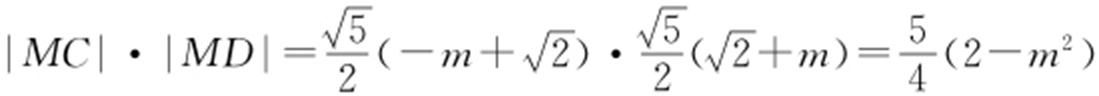 .
.
【考点 】 直线与椭圆的相交问题.
52.(1)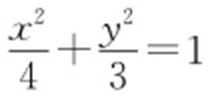 ;(2)
;(2)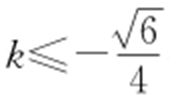 或
或 .
.
【解析 】 (1)设F (c ,0),由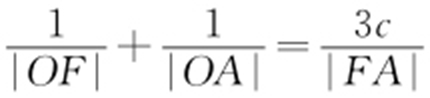 ,即
,即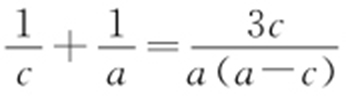 ,可得a 2 -c 2 =3c 2 ,又a 2 -c 2 =b 2 =3,所以c 2 =1,因此a 2 =4,所以椭圆的方程为
,可得a 2 -c 2 =3c 2 ,又a 2 -c 2 =b 2 =3,所以c 2 =1,因此a 2 =4,所以椭圆的方程为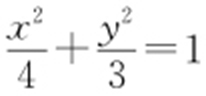 .
.
(2)设直线l 的斜率为k (k ≠0),则直线l 的方程为y =k (x -2).设B (xB ,yB ),由方程组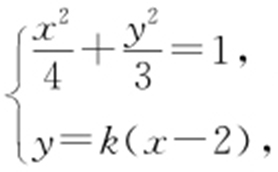 消去y ,整理得(4k 2 +3)x 2 -16k 2 x +16k 2 -12=0.
消去y ,整理得(4k 2 +3)x 2 -16k 2 x +16k 2 -12=0.
解得x =2或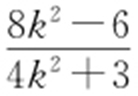 ,由题意得
,由题意得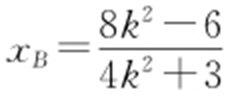 ,从而
,从而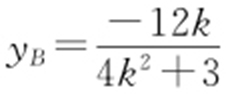 .
.
由(1)知F (1,0),设H (0,yH ),有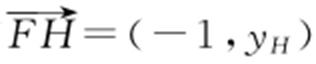 ,
,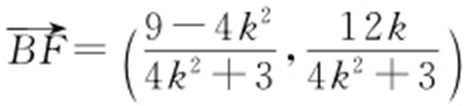 .由BF ⊥HF ,得
.由BF ⊥HF ,得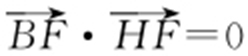 ,所以
,所以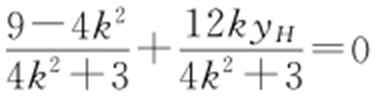 ,解得
,解得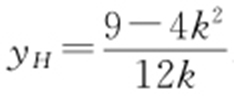 .因此直线MH 的方程为
.因此直线MH 的方程为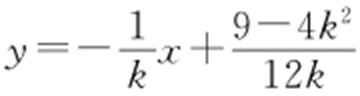 .
.
设M (xM ,yM ),由方程组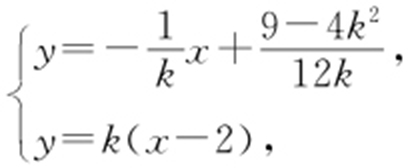 消去y ,解得
消去y ,解得 .在△MAO 中,∠MOA ≤∠MAO ⇔|MA |≤|MO |,即
.在△MAO 中,∠MOA ≤∠MAO ⇔|MA |≤|MO |,即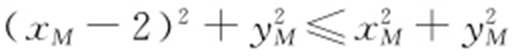 ,化简得xM ≥1,即
,化简得xM ≥1,即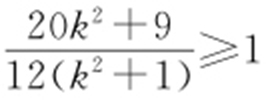 ,解得
,解得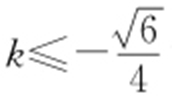 或
或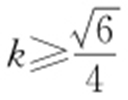 .
.
【考点 】 直线与椭圆的相交问题.
53.(1)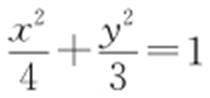 ;(2)
;(2)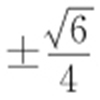 .
.
【解析 】 (1)设F (c ,0),由 ,即
,即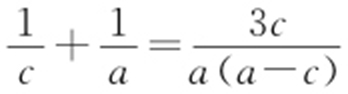 ,可得a 2 -c 2 =3c 2 ,又a 2 -c 2 =b 2 =3,所以c 2 =1,因此a 2 =4,所以椭圆的方程为
,可得a 2 -c 2 =3c 2 ,又a 2 -c 2 =b 2 =3,所以c 2 =1,因此a 2 =4,所以椭圆的方程为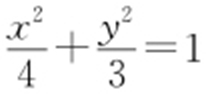 .
.
(2)设直线的斜率为k (k ≠0),则直线l 的方程为y =k (x -2),设B (xB ,yB ),由方程组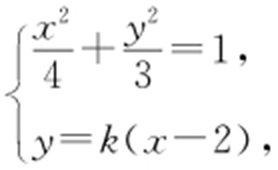 消去y ,整理得(4k 2 +3)x 2 -16k 2 x +16k 2 -12=0,解得x =2或
消去y ,整理得(4k 2 +3)x 2 -16k 2 x +16k 2 -12=0,解得x =2或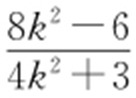 ,由题意得
,由题意得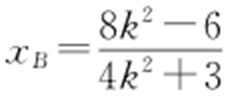 ,从而
,从而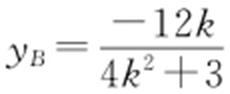 ,由(1)知F (1,0),设H (0,yH ),有
,由(1)知F (1,0),设H (0,yH ),有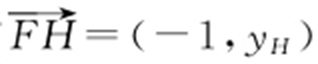 ,
,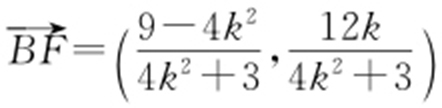 ,由BF ⊥HF ,得
,由BF ⊥HF ,得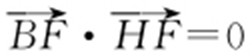 ,所以
,所以 ,解得
,解得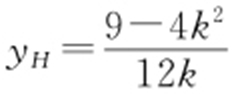 ,因此直线MH 的方程为
,因此直线MH 的方程为 .设M (xM ,yM ),由方程组
.设M (xM ,yM ),由方程组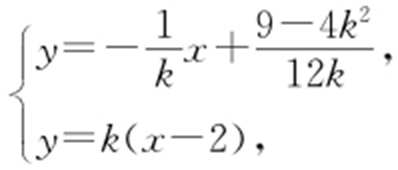 消去 y ,得
消去 y ,得 ,在△MAO 中,∠MOA =∠MAO ⇔|MA |=|MO |,即
,在△MAO 中,∠MOA =∠MAO ⇔|MA |=|MO |,即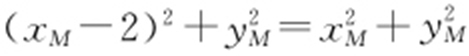 ,化简得xM =1,即
,化简得xM =1,即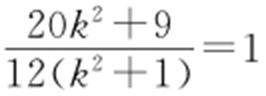 ,解得
,解得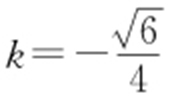 或
或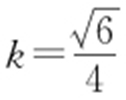 ,所以直线l 的斜率为
,所以直线l 的斜率为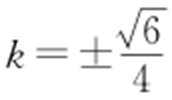 .
.
【考点 】 椭圆的标准方程和几何性质;直线方程.
54.(1)p =2;(2)(-∞,0)∪(2,+∞).
【解析 】 (1)由题意可得抛物线上点A 到焦点F 的距离等于点A 到直线x =-1的距离.由抛物线得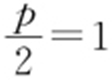 ,即p =2.
,即p =2.
(2)由(1)得抛物线的方程为y 2 =4x ,F (1,0),可设A (t 2 ,2t ),t ≠0,t ≠±1.
因为AF 不垂直于y 轴,可设直线AF :x =sy +1(s ≠0),由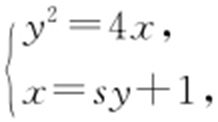 消去x 得y 2 -4sy -4=0,故y 1 y 2 =-4,所以
消去x 得y 2 -4sy -4=0,故y 1 y 2 =-4,所以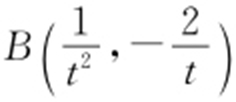 .又直线AB 的斜率为
.又直线AB 的斜率为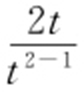 ,故直线FN 的斜率为
,故直线FN 的斜率为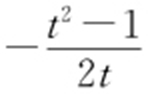 ,从而得直线FN :
,从而得直线FN :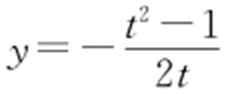 (x -1),直线BN :
(x -1),直线BN : ,所以
,所以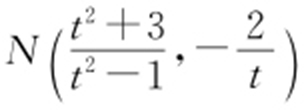 ,设M (m ,0),由A ,M ,N 三点共线得
,设M (m ,0),由A ,M ,N 三点共线得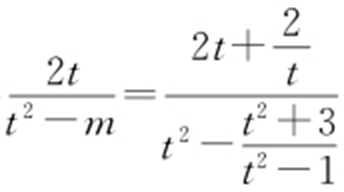 ,于是
,于是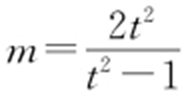 ,经检验,m <0或m >2满足题意.综上,点M 的横坐标的取值范围是(-∞,0)∪(2,+∞).
,经检验,m <0或m >2满足题意.综上,点M 的横坐标的取值范围是(-∞,0)∪(2,+∞).
【考点 】 直线与抛物线的相交问题.
55.(1)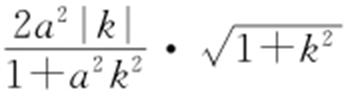 ,(2)
,(2)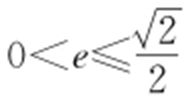 .
.
【解析 】 (1)设直线y =kx +1被椭圆截得的线段为AP ,由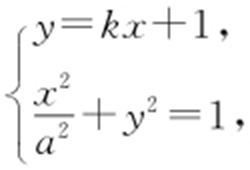 得(1+a 2 k 2 )x 2 +2a 2 kx =0,故x 1 =0,
得(1+a 2 k 2 )x 2 +2a 2 kx =0,故x 1 =0,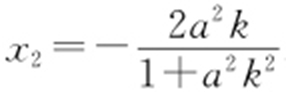 .因此
.因此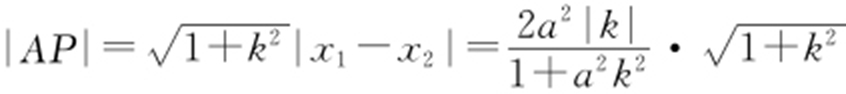 .
.
(2)假设圆与椭圆的公共点有4个,由对称性可设y 轴左侧的椭圆上有两个不同的点P ,Q ,满足|AP |=|A Q |.
记直线AP ,AQ 的斜率分别为k 1 ,k 2 ,且k 1 ,k 2 >0,k 1 ≠k 2 .
由(1)知,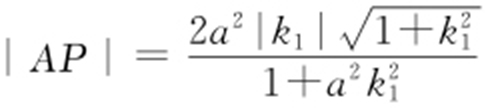 ,
,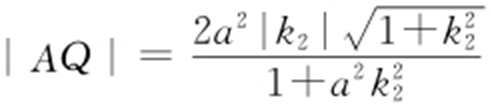 ,故
,故 ,所以
,所以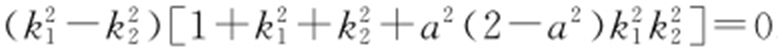 .由于k 1 ≠k 2 ,k 1 ,k 2 >0,得
.由于k 1 ≠k 2 ,k 1 ,k 2 >0,得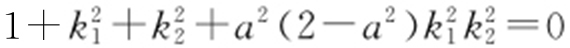 ,因此
,因此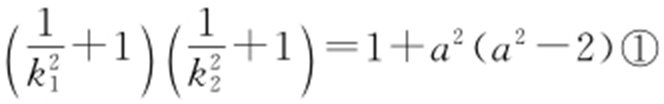 .
.
因为①式关于k 1 ,k 2 的方程有解的充要条件是1+a 2 (a 2 -2)>1,所以 .
.
因此,任意以点A (0,1)为圆心的圆与椭圆至多有3个公共点的充要条件为1<a ≤2,由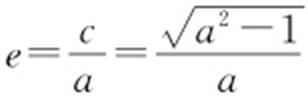 得所求离心率的取值范围为
得所求离心率的取值范围为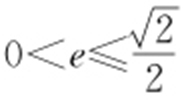 .
.
【考点 】 圆的弦长公式;椭圆的离心率.
56.(1)y 2 =8x ;(2)①(2-p ,-p ),② .
.
【解析 】 (1)抛物线C :y 2 =2px (p >0)的焦点为 .由点
.由点 在直线l :x -y -2=0上,得
在直线l :x -y -2=0上,得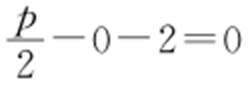 ,即p =4.所以抛物线C 的方程为y 2 =8x .
,即p =4.所以抛物线C 的方程为y 2 =8x .
(2)设P (x 1 ,y 1 ),Q (x 2 ,y 2 ),线段PQ 的中点M (x 0 ,y 0 ).因为点P 和Q 关于直线l 对称,所以直线l 垂直平分线段PQ ,于是直线PQ 的斜率为-1,则可设其方程为y =-x +b .
①由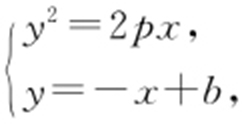 消去x ,得y 2 +2py -2pb =0*.
消去x ,得y 2 +2py -2pb =0*.
因为P 和Q 是抛物线C 上的相异两点,所以y 1 ≠y 2 ,从而Δ =(2p )2 -4(-2pb )>0,化简得p +2b >0.
方程*的两根为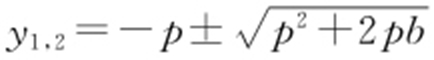 ,从而
,从而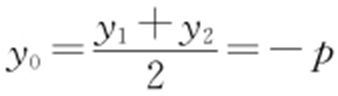 .因为M (x 0 ,y 0 )在直线l 上,所以x 0 =2-p .因此,线段PQ 的中点坐标为(2-p ,-p ).
.因为M (x 0 ,y 0 )在直线l 上,所以x 0 =2-p .因此,线段PQ 的中点坐标为(2-p ,-p ).
②因为M (2-p ,-p )在直线y =-x +b 上,所以-p =-(2-p )+b ,即b =2-2p .
由①知p +2b >0,于是p +2(2-2p )>0,所以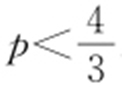 .因此p 的取值范围为
.因此p 的取值范围为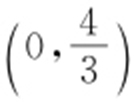 .
.
【考点 】 抛物线的性质.
极坐标与参数方程
57.2.
【考点 】 直角坐标与极坐标的转换.
58.(1)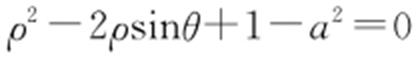 ;(2)a =1.
;(2)a =1.
【解析 】 (1) (t 均为参数)所以x 2 +(y -1)2 =a 2 ①,所以C 1 为以(0,1)为圆心、a 为半径的圆,方程为x 2 +y 2 -2y +1-a 2 =0.因为
(t 均为参数)所以x 2 +(y -1)2 =a 2 ①,所以C 1 为以(0,1)为圆心、a 为半径的圆,方程为x 2 +y 2 -2y +1-a 2 =0.因为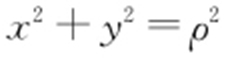 ,
,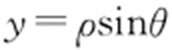 ,所以
,所以 ,此即为C 1 的极坐标方程.
,此即为C 1 的极坐标方程.
(2)C 2 :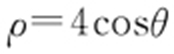 ,两边同乘以
,两边同乘以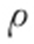 得
得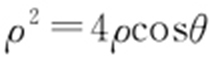 .因为
.因为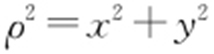 ,
,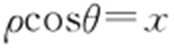 ,所以x 2 +y 2 =4x ,即(x -2)2 +y 2 =4②.
,所以x 2 +y 2 =4x ,即(x -2)2 +y 2 =4②.
C 3 化为普通方程为y =2x ,由题意,C 1 和C 2 的公共方程所在直线即为C 3 ,①-②得,4x -2y +1-a 2 =0,即为C 3 .所以1-a 2 =0,即a =1.
【考点 】 参数方程与直角坐标的转换;极坐标与直角坐标的转换.
59.(1)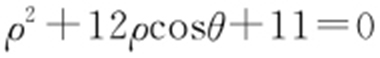 ;(2)
;(2)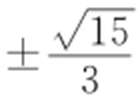 .
.
【解析 】 (1)整理圆的方程,得x 2 +y 2 +12+11=0.
由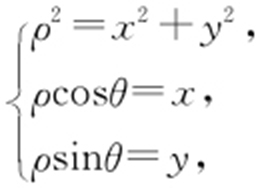 可知圆C 的极坐标方程为
可知圆C 的极坐标方程为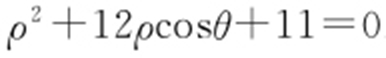 .
.
(2)记直线的斜率为k ,则直线的方程为kx -y =0,由垂径定理及点到直线距离公式,知 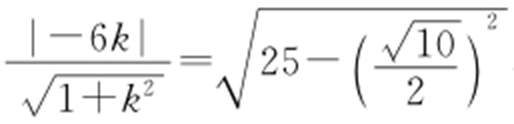 ,即
,即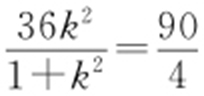 ,整理得
,整理得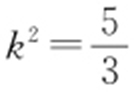 ,则
,则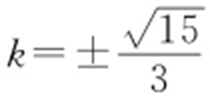 .
.
【考点 】 参数方程与直角坐标的转换;极坐标与直角坐标的转换.
60.(1)C 1 :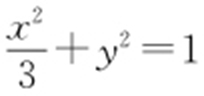 ,C 2 :x +y -4=0;(2)
,C 2 :x +y -4=0;(2)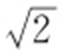 ,
, .
.
【解析 】 (1)C 1 的普通方程为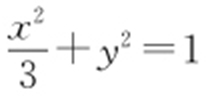 ,C 2 的直角坐标方程为x +y -4=0.
,C 2 的直角坐标方程为x +y -4=0.
(2)由题意,可设点P 的直角坐标为(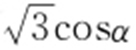 ,sinα ),因为C 2 是直线,所以|PQ |的最小值,即为P 到C 2 的距离d (α )的最小值,
,sinα ),因为C 2 是直线,所以|PQ |的最小值,即为P 到C 2 的距离d (α )的最小值,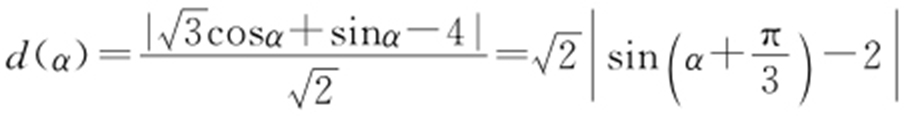 .
.
当且仅当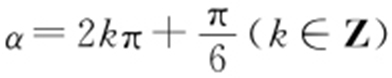 时,d (α )取得最小值,最小值为
时,d (α )取得最小值,最小值为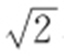 ,此时P 的直角坐标为
,此时P 的直角坐标为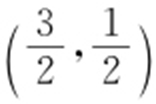 .
.
【考点 】 参数方程与直角坐标的转换;极坐标与直角坐标的转换.
61.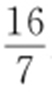 .
.
【解析 】 椭圆C 的普通方程为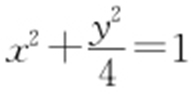 ,将直线l 的参数方程
,将直线l 的参数方程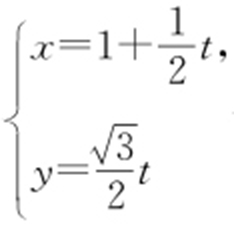 代入
代入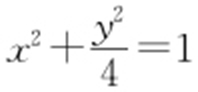 ,得
,得 ,即7t 2 +16t =0,解得t 1 =0,
,即7t 2 +16t =0,解得t 1 =0,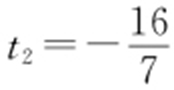 .所以
.所以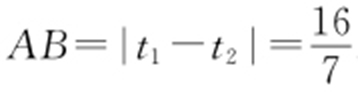 .
.