第一章 直线
1.直线的倾斜角:一条直线向上的方向与 x 轴的正方向 所成的夹角 叫做这条直线的倾斜角,其中直线与x 轴平行或重合时,其倾斜角0° ,故直线倾斜角的范围是[0,π) .
注:当α =90°时,直线l 垂直于x 轴,它的斜率不存在 .
2.直线方程的常用形式:点斜式、截距式、斜截式、一般式.
(1)点斜式:过点(x 0 ,y 0 ),斜率为k 的直线可设为:y -y 0 =k (x -x 0 ) .
适用范围:直线斜率存在(倾斜角不为90°) .
(2)斜截式:斜率为k ,且在y 轴截距为b (或过点(0,b ))的直线可设为y =kx +b .
适用范围:直线斜率存在(倾斜角不为90°) .
(3)截距式:在x 轴上截距为a ,在y 轴截距为b (或者过(a ,0),(0,b )两点)的直线可设为 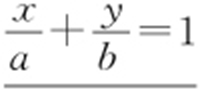 .
.
适用范围:不过原点,且直线倾斜角不等于0°和90° .
(4)一般式:任意直线均可设为Ax +By +C =0 .
适用范围:所有直线 .
3.直线系:对于直线的斜截式方程y =kx +b ,当k ,b 均为确定的数值时,它表示一条确定的直线,如果k ,b 变化时,对应的直线也会变化.
(1)当b 为定值,k 变化时,它们表示过定点(0,b ) 的直线束.
(2)当k 为定值,b 变化时,它们表示一组平行线 .
(3)过两直线l 1 :A 1 x +B 1 y +C 1 =0,l 2 :A 2 x +B 2 y +C 2 =0的交点的直线系方程为 A 1 x +B 1 y +C 1 +λ (A 2 x +B 2 y +C 2 )=0 (λ 为参数,l 2 不包括在内).
4.当斜率一定存在时(l 1 :y =k 1 x +b 1 ,l 2 :y =k 2 x +b 2 ).
(1)l 1 和l 2 是平行不重合的直线: k 1 =k 2 ,b 1 ≠b 2 .
(2)l 1 和l 2 是重合直线: k 1 =k 2 ,b 1 =b 2 .
(3)l 1 和l 2 是垂直的直线: k 1 k 2 =-1 .
5.当斜率不一定存在时(l 1 :A 1 x +B 1 y +C 1 =0,l 2 :A 2 x +B 2 y +C 2 =0).
(1)l 1 和l 2 是平行不重合的直线: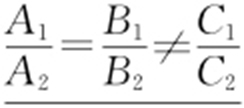 .
.
(2)l 1 和l 2 是重合直线: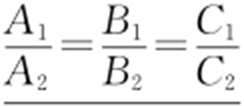 .
.
(3)l 1 和l 2 是垂直的直线: A 1 A 2 +B 1 B 2 =0 .
6.距离问题.
(1)点P (x 1 ,y 1 ),Q (x 2 ,y 2 )的距离为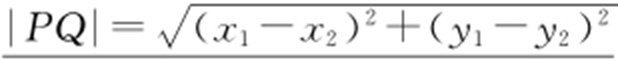 .
.
(2)设点P (x 0 ,y 0 ),直线l :Ax +By +C =0,P 到l 的距离为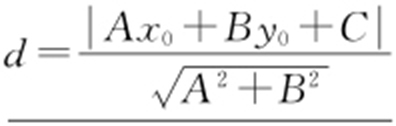 .
.
(3)设两条平行直线l 1 :Ax +By +C 1 =0,l 2 :Ax +By +C 2 =0(C 1 ≠C 2 ),它们之间的距离为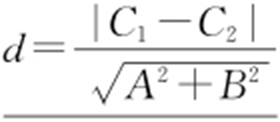 .
.
7.对称问题.
(1)点点对称型
A (x 0 ,y 0 )关于点P (a ,b )对称的点为(2a -x 0 ,2b -y 0 ) .
(2)点线对称型点
A (x 0 ,y 0 )关于直线Ax +By +C =0对称的点为(a ,b ) ,其中: 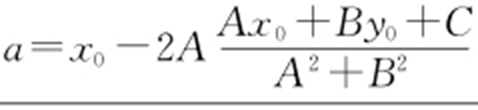 ,
, 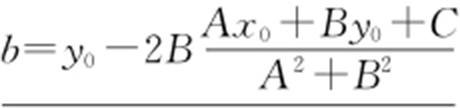 .
.
(3)线点对称型
直线Ax +By +C =0关于点P (x 0 ,y 0 )对称的线为 Ax +By +D =0 ,其中:Ax 0 +By 0 +C +Ax 0 +By 0 +D =0 .
(4)线线对称型
直线ax +by +c =0关于直线Ax +By +C =0对称的直线为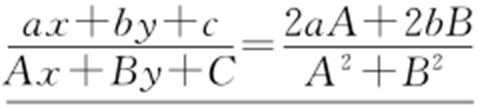 .
.
8.线性规划问题.
(1)可行域的快速判定
二元一次不等式ax +by +c >0,当b 为正时即为线上侧,当b 为负时即为线下侧;二元一次不等式ax +by +c <0,当b 为负时即为线上侧,当b 为正时即为线下侧 .
(2)目标函数的基本类型
①截距型: z =ax +by +c .
②斜率型: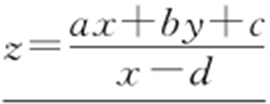 .
.
③距离型: z =ax 2 +by 2 +cx +dy +f .
考点1 直线的倾斜角与斜率
例题
【例1 】(2014·武清期中) 已知直线的斜率范围是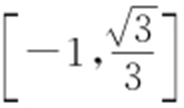 ,求倾斜角的范围;已知直线的斜率范围是(
,求倾斜角的范围;已知直线的斜率范围是(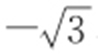 ,+∞),求倾斜角的范围.
,+∞),求倾斜角的范围.
条件 斜率⇒倾斜角.
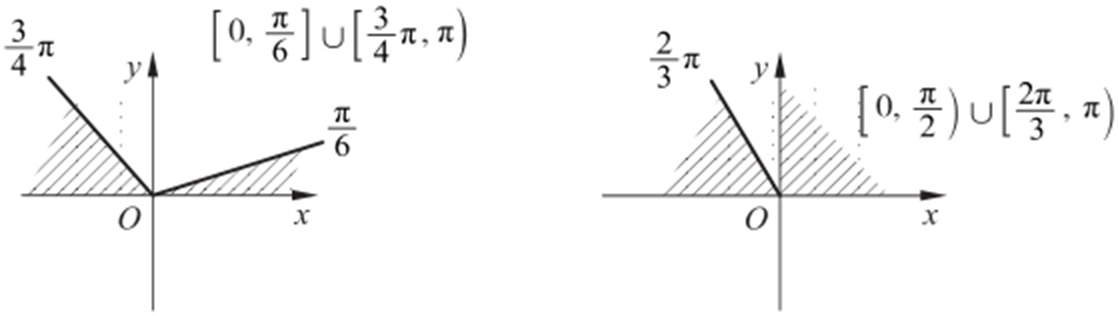
总结
熟练斜率与倾斜角对应值的相互转化,掌握k =tanθ 函数图像.此题也可利用k =tanθ 的图像来求k 与θ .
【例2 】(2011·吉安期末) 已知直线l 的方程:y =(m 2 -1)x +3(m ∈R ),则l 的倾斜角的范围是( ).
条件 k =m 2 -1⇒k ≥-1.
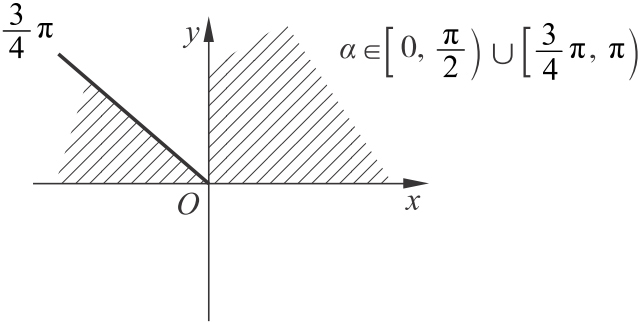
解析 y =(m 2 -1)x +3⇒k =m 2 -1,由于m 2 ≥0,所以m 2 -1≥-1,即k ≥-1⇔tanα ≥-1.
故选:C.
总结
熟悉斜率与倾斜角.
【例3 】(2013·贵阳月考) 已知点A (3,2),B (-4,1),C (0,-1),过点C 的直线l 与线段AB 有公共点,l 的斜率k 的取值范围是 .
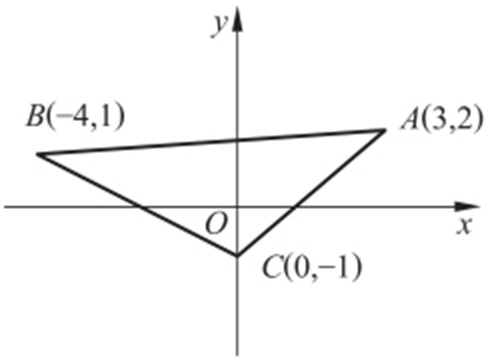
条件 过C 的直线l 与线段AB 相交⇒直线l 介于CA 与CB 之间.
解析 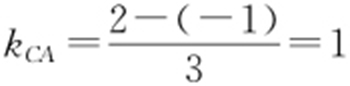 ,
,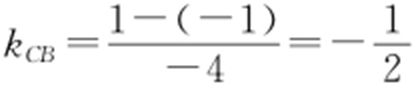 ,斜率由kCA →直角→kCB .
,斜率由kCA →直角→kCB .
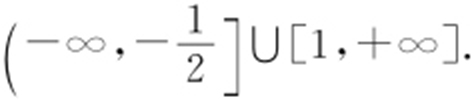
总结
掌握斜率公式,并熟悉斜率在倾斜角为[0,π)间的变化过程.
练习
1.(2014·东台期中) 若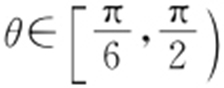 ,则直线2x cosθ +3y +1=0的倾斜角的取值范围为( ).
,则直线2x cosθ +3y +1=0的倾斜角的取值范围为( ).
2.(2013·广州模考) 设点A (2,-3),B (-3,-2),直线l 过点P (1,1)且与线段AB 相交,则l 的斜率k 的取值范围为( ).
考点2 直线的五种表达式及位置关系
例题
【例1 】(2015·唐山期中) 已知直线(a -2)y =(3a -1)x -1.
(1)求证:无论a 为何值,直线总经过第一象限;
(2)直线l 是否有可能不经过第二象限?若有可能,求出a 的范围;若不可能,说明理由.
(1)条件 过第一象限⇒过第一象限的定点.
解析 (a -2)y =(3a -1)x -1, .
.
总结
直线过定点问题需将参数进行分离,再通过方程组进行求解.
(2)条件 不经过第二象限⇒y =kx +b 中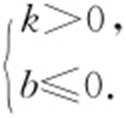
解析 当a ≠2时,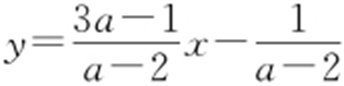 ,
,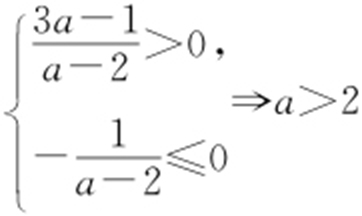 .
.
当a =2时,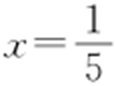 ,不经过第二象限.综上,a ≥2.
,不经过第二象限.综上,a ≥2.
总结
直线过象限问题一般转化为斜截式考虑.
【例2 】(2016·上海文理·3) 已知平行直线l 1 :2x +y -1=0,l 2 :2x +y +1=0,则l 1 与l 2 的距离是 .
条件 l 1 与l 2 距离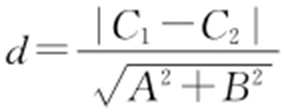 .
.
总结
平行线距离公式使用过程中切记两条直线中的A ,B 要相同.
【例3 】(2014·四川理·9) 设m ∈R ,过定点A 的动直线x +my =0和过定点B 的动直线mx -y -m +3=0交于点P (x ,y ),则|PA |·|PB |的最大值是 .
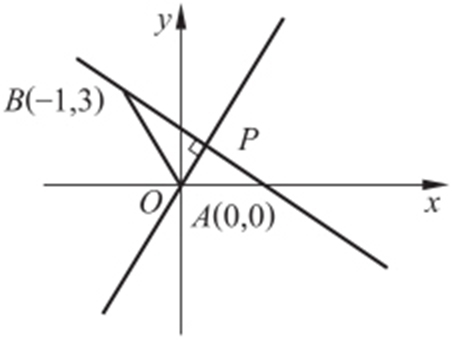
解析 A (0,0),B (-1,3),又因为x +my =0与mx -y -m +3=0垂直,可得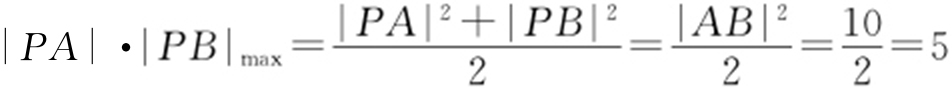 .
.
总结
l 1 与l 2 垂直(一般式)⇔A 1 A 2 +B 1 B 2 =0.
【例4 】(2013·新课标2理·12) 已知A (-1,0),B (1,0),C (0,1),直线y =ax +b (a >0)将△ABC 分割为面积相等的两部分,则b 的取值范围是( ).
条件 y =ax +b 分△ABC 为面积相等两部分⇒三角形面积公式与点到直线距离公式.
解析 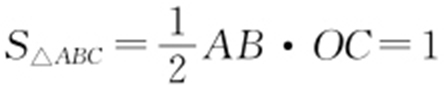 ,直线y =ax +b (a >0)与x 轴的交点为
,直线y =ax +b (a >0)与x 轴的交点为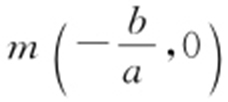 .由
.由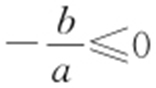 ,可知点M 在射线OA 上,设直线和BC 交点为N ,
,可知点M 在射线OA 上,设直线和BC 交点为N ,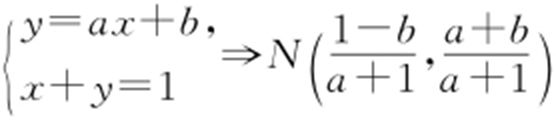 .
.
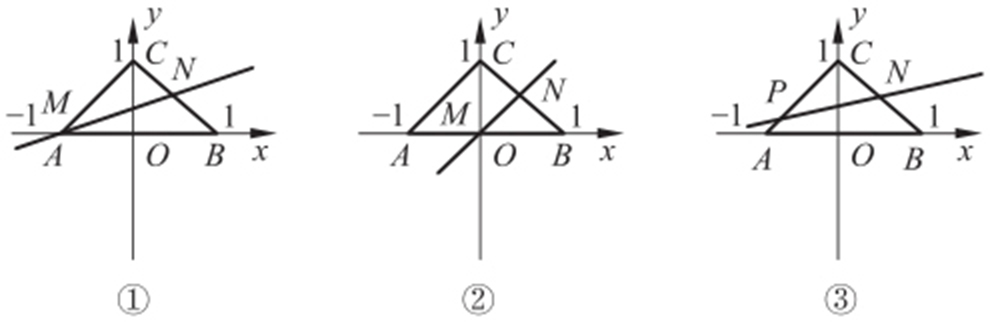
①点M 与A 重合,则N 为BC 中点,则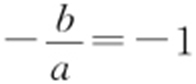 ,
,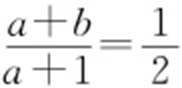 .
.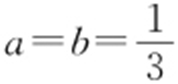 .
.
②点M 在OA 间,则N 在BC 间,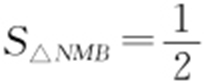 ,即
,即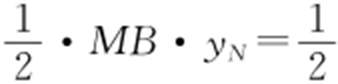 .
.
.
③点M 在A 左侧,则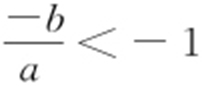 ,所以b >a .设y =ax +b 与AC 交点为P ,则
,所以b >a .设y =ax +b 与AC 交点为P ,则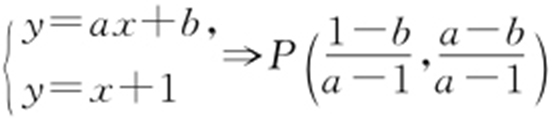 .
.
又因为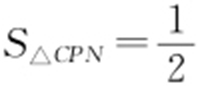 ,即
,即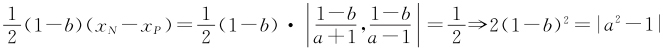 ,b >a >0,0<a <1,所以2(1-b )2 =|a 2 -1|=1-a 2 ,所以
,b >a >0,0<a <1,所以2(1-b )2 =|a 2 -1|=1-a 2 ,所以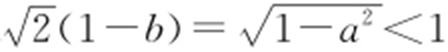 ,所以
,所以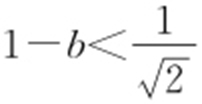 ,即
,即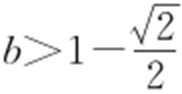 .
.
综上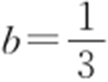 ,
,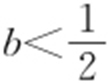 ,
,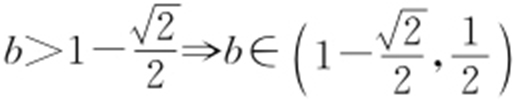 .故选:B.
.故选:B.
总结
分类讨论思想.
【例5 】(2011·安徽理·15) 平面直角坐标系中,如果x 与y 都是整数,那么就称点(x ,y )为整点,下列命题中正确的是 (写出所有正确命题的编号).
①存在这样的直线,既不与坐标轴平行又不经过任何整点;
②如果k 与b 都是无理数,则直线y =kx +b 不经过任何整点;
③直线l 经过无穷多个整点,当且仅当l 经过两个不同的整点;
④直线y =kx +b 经过无穷多个整点的充分必要条件是:k 与b 都是有理数;
⑤存在恰经过一个整点的直线.
条件 出现“存在”或“如果”⇒举反例来判断.
解析 ①若x ,y 为整数,则x +y 也为整数,故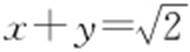 既不平行于坐标轴,也不经过任何整点,即①正确.
既不平行于坐标轴,也不经过任何整点,即①正确.
②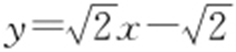 过(1,0),故②错.
过(1,0),故②错.
③若l 经过M (m 1 ,n 1 ),N (m 2 ,n 2 ),其中m 1 ,m 2 ,n 1 ,n 2 均为整数.当m 1 =m 2 或n 1 =n 2 时,直线l 方程为x =m 1 或y =n 1 ,显然过无穷多个整点.当m 1 ≠m >2 且n 1 ≠n 2 时,直线l 的方程为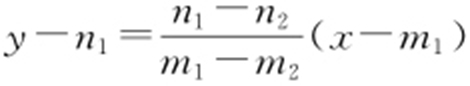 ,则直线l 过点((k +1)m 1 -km 2 ,(k +1)n 1 -kn 2 ),k ∈Z .这些整数均为整点且有无穷多个,即直线l 经过无穷多整点,③正确.
,则直线l 过点((k +1)m 1 -km 2 ,(k +1)n 1 -kn 2 ),k ∈Z .这些整数均为整点且有无穷多个,即直线l 经过无穷多整点,③正确.
④x ,y 为整数时,y -x 还是整数,故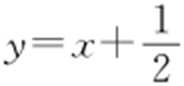 不经过任何整点.当k ,b 为有理数,并不能保证l :y =kx +b 过无穷多个整点,④错.
不经过任何整点.当k ,b 为有理数,并不能保证l :y =kx +b 过无穷多个整点,④错.
⑤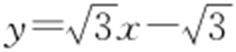 过(1,0),⑤正确.
过(1,0),⑤正确.
故选:①③⑤.
总结
对于新定义的题目,大家做题时可考虑举一些例子和数据来判断正误.
练习
1.(2010·广东模考) 已知直线l :kx -y +1+2k =0(k ∈R ).
(1)证明:直线l 过定点;
(2)若直线不经过第四象限,求k 的取值范围;
(3)若直线l 交x 轴负半轴于A ,交y 轴正半轴于B ,△AOB 的面积为S ,求S 的最小值并求此时直线l 的方程.
2.(2014·四川理·8改编) 设m ∈R ,过定点A 的动直线x +my =0和过定点B 的动直线mx -y -m +3=0交于点P (x ,y ),则|PA |+|PB |的取值范围是( ).
3.(2011·北京文·8) 已知点A (0,2),B (2,0).若点C 在函数y =x 2 的图像上,则使得△ABC 的面积为2的点C 的个数为( ).
A.4
B.3
C.2
D.1
4.(2013·辽宁文理·9) 已知点O (0,0),A (0,b ),B (a ,a 3 ).若△ABC 为直角三角形,则必有( ).
5.(2011·北京理·8) 设A (0,0),B (4,0),C (t +4,4),D (t ,4)(t ∈R ).记N (t )为平行四边形ABCD 内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则函数N (t )的值域为( ).
A.{9,10,11}
B.{9,10,12}
C.{9,11,12}
D.{10,11,12}
考点3 距离和对称
例题
【例1 】(2015·枣阳月考) 已知两点A (3,-3),B (5,1)和直线l :y =x ,在直线l 上求一点P 使|PA |+|PB |最小.
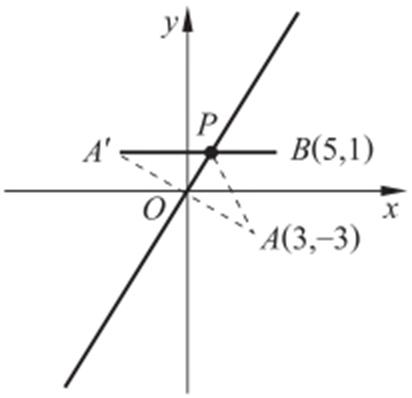
条件 (|PA |+|PB |)min ≥|AB |⇒(|PA |+|PB |)min =|AB |.
解析 作A 关于l 对称点A′ ,A′ (-3,3),|PA |=|PA′ |.连A′B 交l 于P ,P 即为所求,lA′B :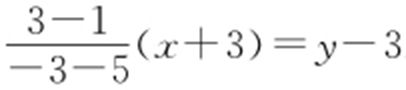 .此时|PA′ |+|PB |=|A′B |最小,联立
.此时|PA′ |+|PB |=|A′B |最小,联立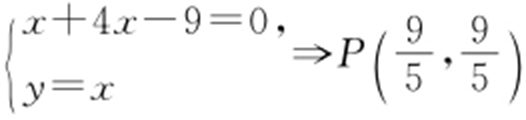 .
.
总结
【例2 】(2011·秦兴期中) 已知光线通过点A (2,3),经直线x +y +1=0反射,其反射光线通过点B (1,1),求入射光线和反射光线所在的方程.
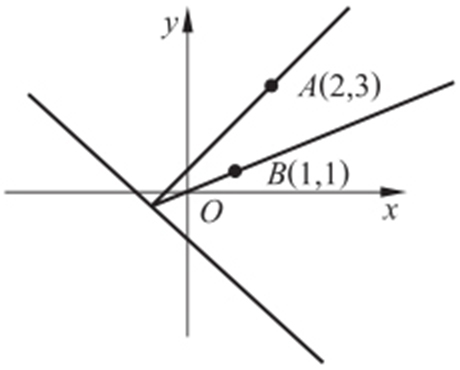
条件 求入射光线所在直线方程⇒求入射光线上两点⇒求反射光线上点的对称点.
解析 设B (1,1)关于l 的对称点为B′ (a ,b ),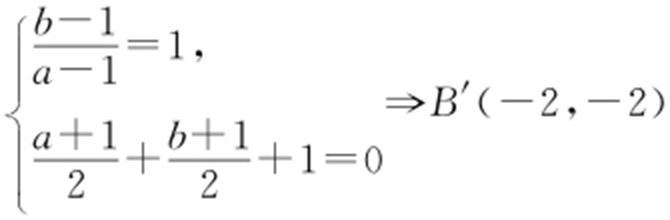 .
.
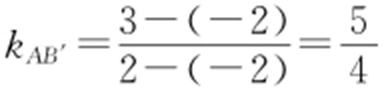 ,所以lAB′ :
,所以lAB′ :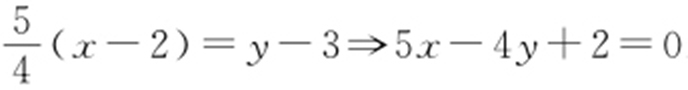 .同理,反射光线为4x -5y +1=0.
.同理,反射光线为4x -5y +1=0.
总结
光线反射问题往往被转化为对称问题求解.
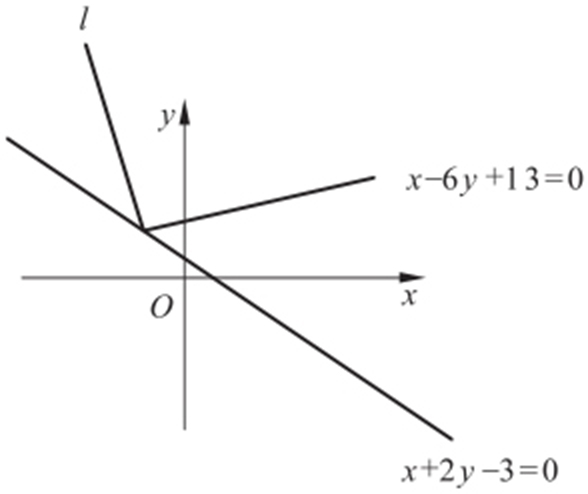
【例3 】(2011·丰南期中) 已知光线的入射线所在直线的方程为x -6y +13=0,入射线在定直线x +2y -3=0上反射,求反射光线所在直线方程.
条件 反射光线所在直线方程⇔线线对称.
解析 在x -6y +13=0上找一点C (-13,0),求C (-13,0)关于x +2y -3=0的对称点.
根据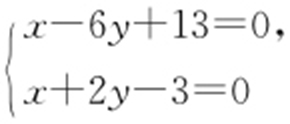 的交点在l 上,得l 27x +14y -1=0.
的交点在l 上,得l 27x +14y -1=0.
练习
1.(2010·广东模考) 已知两点A (-3,3),B (5,1)和直线l :y =x ,在直线l 上求一点P ,使||PA |-|PB ||最大.
2.(2015·舒城月考) 光线从A (-2,3)出发,经直线x -y +10=0反射,反射光线经过点C (1,2),求入射光线所在直线方程.
3.(2011·深圳期中) 已知光线的入射线所在直线的方程为2x +y -3=0,入射线在定直线x +y +4=0上反射,求反射光线所在直线方程.
考点4 线性规划
例题
1.目标函数z =ax +by 型(截距型)
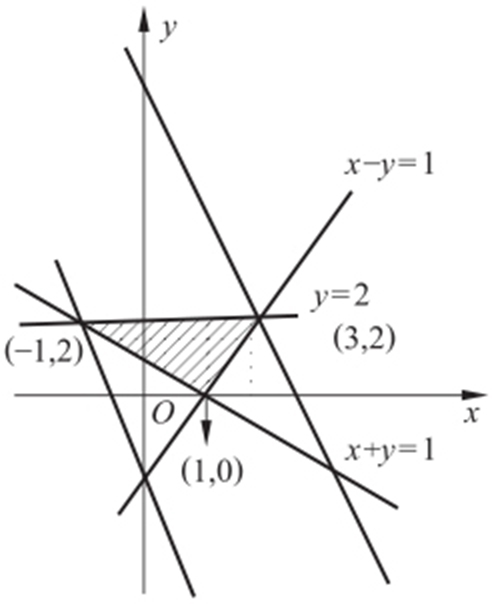
【例1 】(2012·广东理·5) 已知变量x ,y 满足约束条件则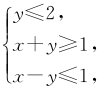 z =3x +y 的最大值为( ).
z =3x +y 的最大值为( ).
A.12
B.11
C.3
D.-1
条件 z =3x +y 最值⇒y =-3x +z 截距最值.
解析 过点(-1,2),z min =-1.过点(3,2),z max =11.故选:B.
总结
常规z =ax +by 型最值问题转化为的截距最值问题.
【例2 】(2012·新课标理·14) 设x ,y 满足约束条件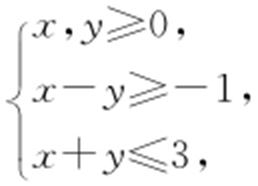 则z =x -2y 的取值范围为 .
则z =x -2y 的取值范围为 .
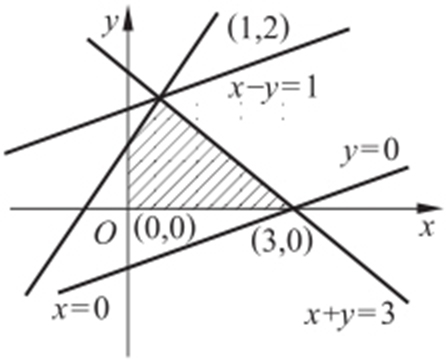
条件 z =x -2y 最值⇒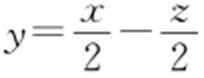 的截距最值.
的截距最值.
解析 过点(1,2),z min =-3.过点(3,0),z max =3.z ∈[-3,3].
总结
常规z =ax +by 型最值问题转化为的截距最值问题.
2.目标函数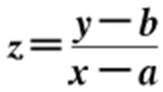 型(斜率型)
型(斜率型)
【例3 】(2012·福建模考) 若变量x ,y 满足约束条件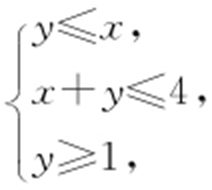 则
则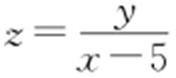 的范围为 .
的范围为 .
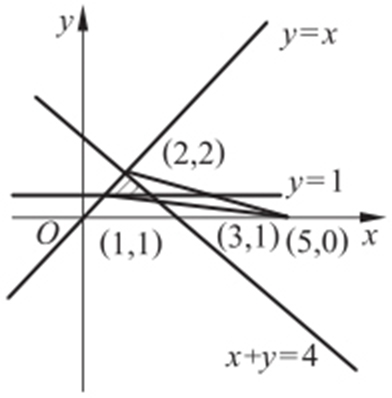
条件  范围⇒(x ,y )与(5,0)组成斜率范围.
范围⇒(x ,y )与(5,0)组成斜率范围.
解析 (5,0)与(1,1)两点相连,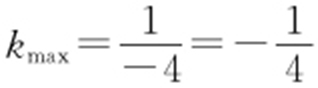 .(5,0)与(2,2)两点相连,
.(5,0)与(2,2)两点相连,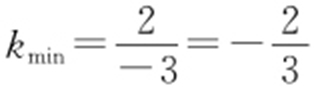 .
.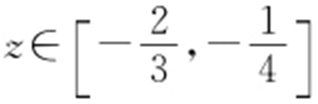 .
.
总结
与(a ,b )组成斜率.
3.目标函数z =(x -a )2 +(y -b )2 型(距离型)
【例4 】(2016·江苏理·12) 已知实数x ,y 满足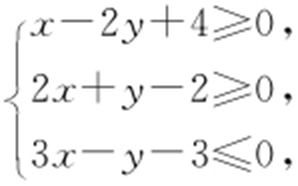 则x 2 +y 2 的取值范围是 .
则x 2 +y 2 的取值范围是 .
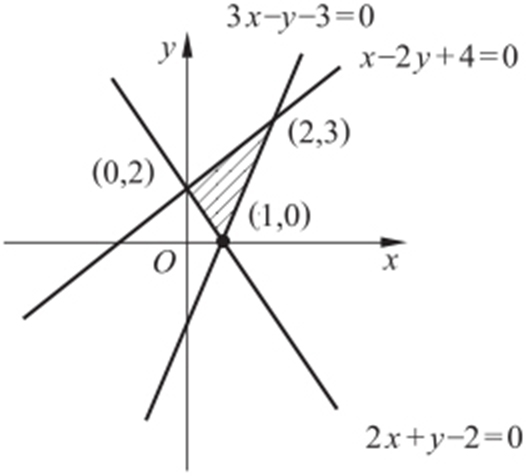
条件 z =x 2 +y 2 最值⇒(x ,y )与(0,0)距离最大值.
解析 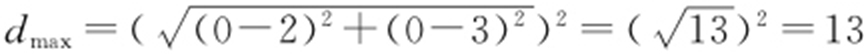 ,d min 为(0,0)到2x +y -2=0距离.
,d min 为(0,0)到2x +y -2=0距离.
总结
z =(x -a )2 +(y -b )2 求最值等价于(x ,y )到(a ,b )距离的平方的最值.
4.含参型
【例5 】(2013·新课标2理·9) 已知a >0,x ,y 满足约束条件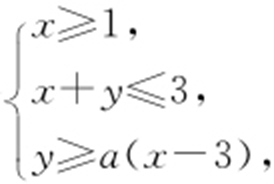 若z =2x +y 的最小值是1,则a =( ).
若z =2x +y 的最小值是1,则a =( ).
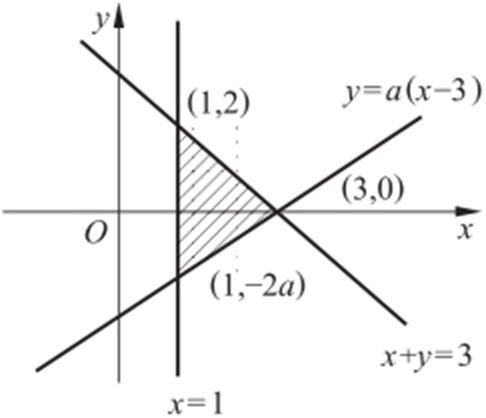
条件 z =2x +y 最小值为1⇒y =-2x +z ,求z 最小值,即截距最小值为1.
解析 y =-2x +z 在过(1,-2a )截距最小,所以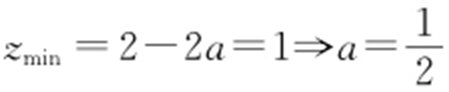 .故选:B.
.故选:B.
总结
,求截距最值.
【例6 】(2013·浙江理·13,文·15) 设z =kx +y ,其中实数x ,y 满足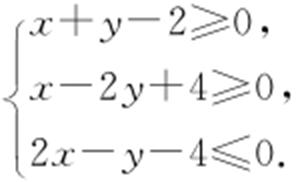 若z 的最大值为12,则实数k = .
若z 的最大值为12,则实数k = .
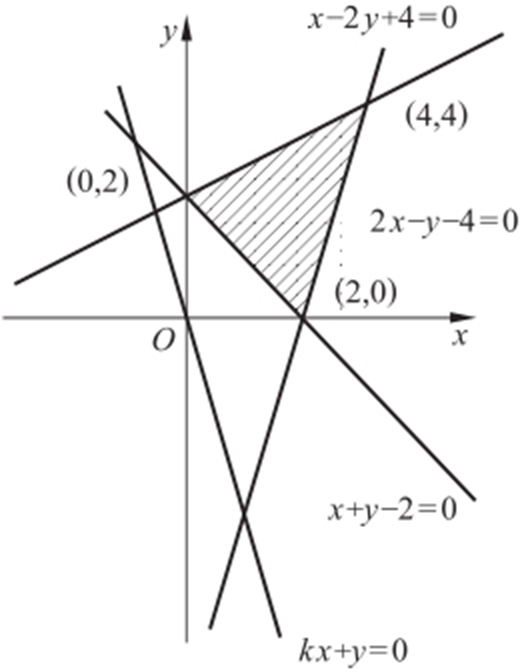
条件 z =kx +y 最大值为12⇒y =-kx +z 截距最大为12.
解析 (1)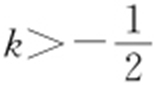 时,y =-kx +z 在(4,4)取最大,z max =4k +4=12,k =2.
时,y =-kx +z 在(4,4)取最大,z max =4k +4=12,k =2.
(2)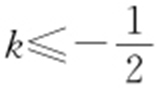 时,y =-kx +z 在(0,2)取最大,z max =0×k +2=12,k ∈∅.
时,y =-kx +z 在(0,2)取最大,z max =0×k +2=12,k ∈∅.
综上,k =2.
总结
求截距最值.但要注意k 分类讨论.
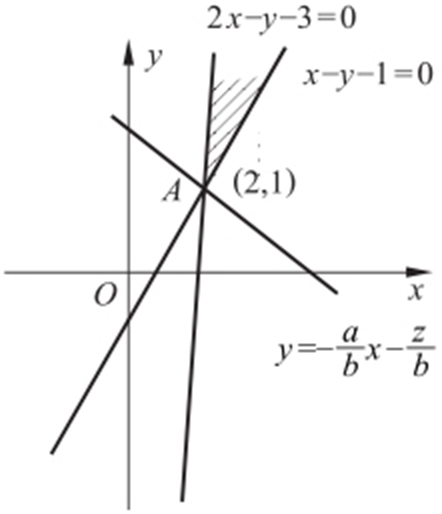
【例7 】(2014·山东文·10,理·9) 已知x ,y 满足的约束条件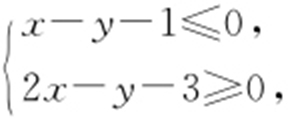 当目标函数z =ax +by (a >0,b >0)在该约束条件下取得最小值
当目标函数z =ax +by (a >0,b >0)在该约束条件下取得最小值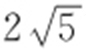 时,a 2 +b 2 的最小值为( ).
时,a 2 +b 2 的最小值为( ).
A.5
B.4
C.
D.2
条件 z =ax +by 取最小值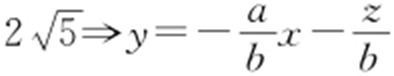 最小值
最小值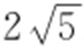 .
.
解析 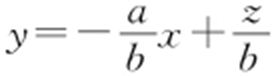 过点(2,1),则
过点(2,1),则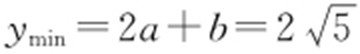 ,所以
,所以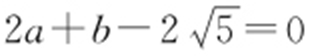 ,所以
,所以 .故选:B.
.故选:B.
总结
求截距最值.
练习
1.(2016·新课标3理·13) 若x ,y 满足约束条件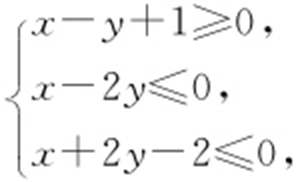 则z =x +y 的最大值为 .
则z =x +y 的最大值为 .
2.(2013·新课标2文·3) 设x ,y 满足约束条件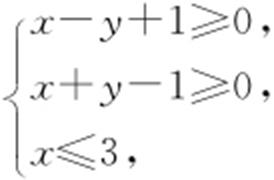 则z =2x -3y 的最小值是( ).
则z =2x -3y 的最小值是( ).
A.-7
B.-6
C.-5
D.-3
3.(2013·四川文·8) 若变量x ,y 满足约束条件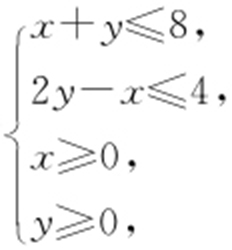 且z =5y -x 的最大值为a ,最小值为b ,则a -b 的值是( ).
且z =5y -x 的最大值为a ,最小值为b ,则a -b 的值是( ).
A.48
B.30
C.24
D.16
4.(2016·新课标1理·16) 某高科技企业生产产品A 和产品B 需要甲、乙两种新型材料.生产一件产品A 需要甲材料1.5kg、乙材料1kg,用5个工时;生产一件产品B 需要甲材料0.5kg、乙材料0.3kg,用3个工时,生产一件产品A 的利润为2100元,生产一件产品B 的利润为900元.该企业现有甲材料150kg、乙材料90kg,则在不超过600个工时的条件下,生产产品A 、产品B 的利润之和的最大值为 元.
5.(2013·山东理·6,文·14) 在平面直角坐标系xOy 中,M 为不等式组: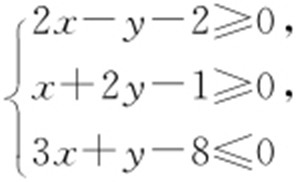 所表示的区域上一动点,则直线OM 斜率的最小值为( ).
所表示的区域上一动点,则直线OM 斜率的最小值为( ).
6.(2016·山东文理·4) 若变量x ,y 满足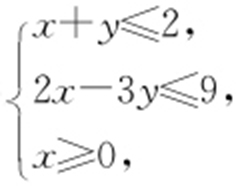 则x 2 +y 2 的最大值是( ).
则x 2 +y 2 的最大值是( ).
A.4
B.9
C.10
D.12
7.(2013·大纲文·15) 记不等式组 所表示的平面区域为D .若直线y =a (x +1)与D 有公共点,则a 的取值范围是 .
所表示的平面区域为D .若直线y =a (x +1)与D 有公共点,则a 的取值范围是 .
8.(2014·安徽理·5) x ,y 满足约束条件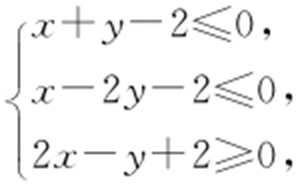 若z =y -ax 取得最大值的最优解不唯一,则实数a 的值为 .
若z =y -ax 取得最大值的最优解不唯一,则实数a 的值为 .
9.(2013·大纲理·15) 设关于x ,y 的不等式组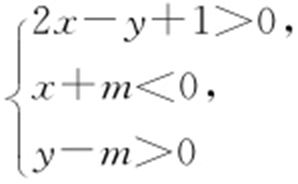 表示的平面区域内存在点P (x 0 ,y 0 )满足x 0 -2y 0 =2,求得m 的取值范围是( ).
表示的平面区域内存在点P (x 0 ,y 0 )满足x 0 -2y 0 =2,求得m 的取值范围是( ).
微信公众号:ncxdf高中数学;高考数学透析分享QQ群:590948624.
高考分数段一分800人,大学好的专业才录取300人,差一分错过好专业,差5分错过好学校.
——彭伟明老师
黑哥细数高考惨案1:选择题把B涂成D.
——彭伟明老师
黑哥细数高考惨案2:填空题书写不规范.
——彭伟明老师
黑哥细数高考惨案3:概率统计算错小概率.
——彭伟明老师
黑哥细数高考惨案4:立体几何建完系却写错点坐标.
——彭伟明老师
黑哥细数高考惨案5:导数题第一问就求错导数.
——彭伟明老师
黑哥细数高考惨案6:圆锥曲线算错小过程.
——彭伟明老师
班规:上课可以说话,但是不能发出声音;上课可以睡觉,但是不能闭上眼睛.
——邓亚东老师
逃课、上网、早睡、晚起统统都无所谓,反正高考又不是只能考一次.
——邓亚东老师
学习数学没有必要背任何的公式,因为高考的时候,监考老师会把它们统统抄在黑板上.
——邓亚东老师
家里有500万,不愁吃不愁穿,难道还需要学习?20年后,500万只能买一个手机壳.
——邓亚东老师
隔壁班的女神清新、优雅、端庄,人家读高一,你在新东方,人家读高二,你在新东方,人家大学毕业,你还在新东方,800个座位不锈钢.
——邓亚东老师
爽,既不会凭空产生,也不会凭空消失,只会从一种形态转化为另外一种形态.
——邓亚东老师
很多同学很努力,但是高中数学每次月考、期中或期末考成绩都很差,大概50分,和那些不读书的人一样,但是我还是要告诉大家,充满智慧的50分,和乱猜乱碰的50分是不一样的.
——邓亚东老师
一个人一生中的运气是守恒的,如果你高一在做数学选择题的时候总是猜,那么等到了高考的时候就一个选项都猜不对了.
——邓亚东老师
















