第3章 椭圆
1.定义:动点到两定点距离之和等于定值且大于两定点距离时 的轨迹称为椭圆.即|MF 1 |+|MF 2 |=2a (2a >|F 1 F 2 |).
这两个定点称为椭圆的焦点 ,两焦点的距离称为椭圆的焦距 .
特别地:
①当|MF 1 |+|MF 2 |=2a (2a =|F 1 F 2 |)时,表示点M 的轨迹为线段F 1 F 2 ;
②当|MF 1 |+|MF 2 |=2a (2a <|F 1 F 2 |)时,表示点M 的轨迹不存在 .
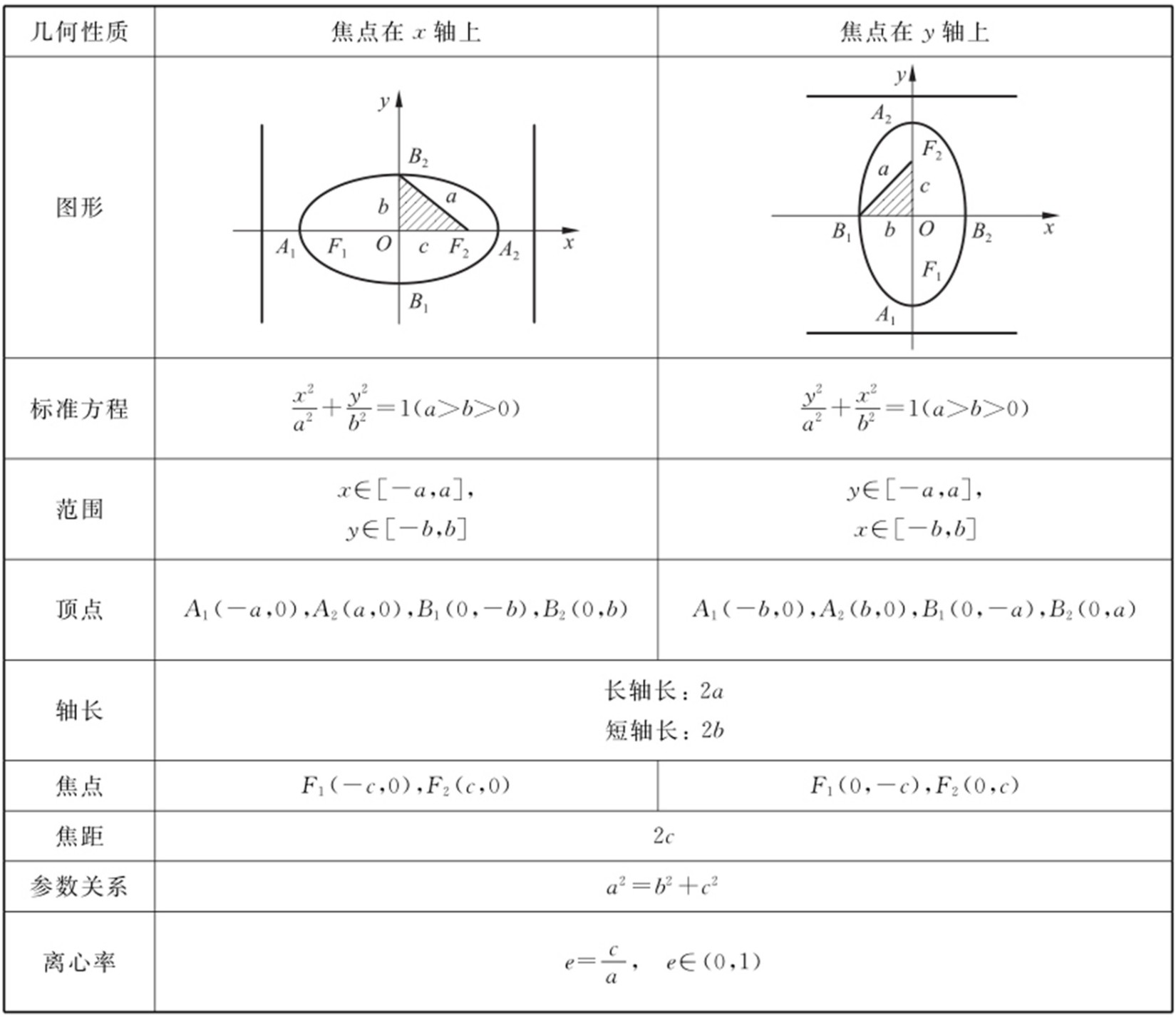
2.椭圆的几何性质.
考点1 椭圆的定义
例题
【例1 】(2015·衡水期末) 方程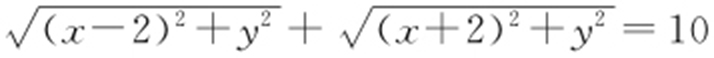 的化简结果是( ).
的化简结果是( ).
条件 将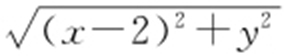 转化为点(x ,y )到点(2,0)的距离,将
转化为点(x ,y )到点(2,0)的距离,将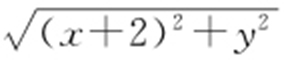 转化为(x ,y )到点(-2,0)的距离.
转化为(x ,y )到点(-2,0)的距离.
解析 根据椭圆的定义.|PF 1 |+|PF 2 |=2a =10>4,所以a =5,c =2,即a 2 =25,c 2 =4,b 2 =21,可得椭圆的方程为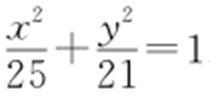 .故选:B.
.故选:B.
【例2 】(2016·永州三模) 设定点M 1 (0,-3),M 2 (0,3),动点P 满足条件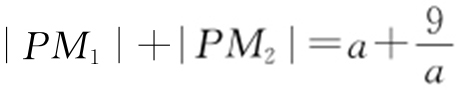 (其中a 是正常数),则点P 的轨迹是( ).
(其中a 是正常数),则点P 的轨迹是( ).
A.椭圆
B.线段
C.椭圆或线段
D.不存在
条件  (a >0)(基本不等式).
(a >0)(基本不等式).
解析 当|PM 1 |+|PM 2 |=6时,点P 的轨迹是线段M 1 M 2 ,当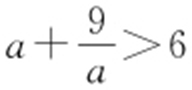 时,点P 是椭圆.故选:C.
时,点P 是椭圆.故选:C.
总结
熟悉椭圆定义:|PF 1 |+|PF 2 |=2a >|F 1 F 2 |.若|PF 1 |+|PF 2 |=2a =|F 1 F 2 |,则P 轨迹为线段F 1 F 2 .
练习
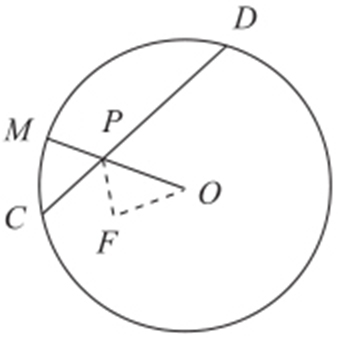
1.(2016·长春二模) 如图,一圆形纸片的圆心为O ,F 是圆内一定点,M 是圆周上一动点,把纸片折叠使M 与F 重合,然后抹平纸片,折痕为CD ,设CD 与OM 交于点P ,则点P 的轨迹是( ).
A.椭圆
B.双曲线
C.抛物线
D.圆
2.(2016·淮南一模) 已知两点F 1 (-1,0),F 2 (1,0),且|F 1 F 2 |是|PF 1 |与|PF 2 |的等差中项,则动点P 的轨迹方程是( ).
考点2 椭圆的方程
例题
【例1 】(2011·江西理·14) 若椭圆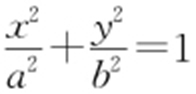 的焦点在x 轴上,过点
的焦点在x 轴上,过点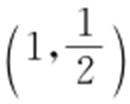 作圆x 2 +y 2 =1的切线,切点分别为A ,B ,直线AB 恰好经过椭圆的右焦点和上顶点,则椭圆方程是 .
作圆x 2 +y 2 =1的切线,切点分别为A ,B ,直线AB 恰好经过椭圆的右焦点和上顶点,则椭圆方程是 .
条件 利用过点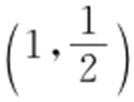 作圆x 2 +y 2 =1的切线,切点为A ,B ,求出A ,B 的坐标,即可求出a ,b ,c .
作圆x 2 +y 2 =1的切线,切点为A ,B ,求出A ,B 的坐标,即可求出a ,b ,c .
解析 因为x =1是圆x 2 +y 2 =1的一条切线,切点为A 点(1,0),则c =1.
设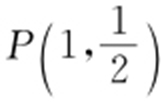 ,则
,则 .因为OP ⊥AB ,所以kAB =-2,则直线AB 的方程为y =-2(x -1).它与y 轴的交点为(0,2),所以b =2,a 2 =b 2 +c 2 =5,故椭圆方程为
.因为OP ⊥AB ,所以kAB =-2,则直线AB 的方程为y =-2(x -1).它与y 轴的交点为(0,2),所以b =2,a 2 =b 2 +c 2 =5,故椭圆方程为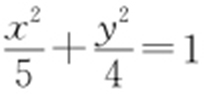 .
.
【例2 】(2013·新课标1理·10) 已知椭圆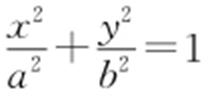 (a >b >0)的右焦点为F (3,0),过点F 的直线交椭圆于A ,B 两点.若AB 的中点坐标为(1,-1),则椭圆的方程为( ).
(a >b >0)的右焦点为F (3,0),过点F 的直线交椭圆于A ,B 两点.若AB 的中点坐标为(1,-1),则椭圆的方程为( ).
条件 利用点差法解决椭圆中点弦问题.
解析 设A (x 1 ,y 1 ),B (x 2 ,y 2 ),则x 1 +x 2 =2,y 1 +y 2 =-2.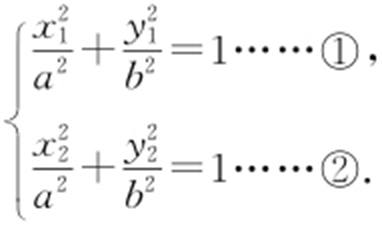 ①-②得,
①-②得,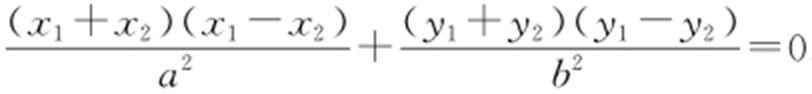 .
.
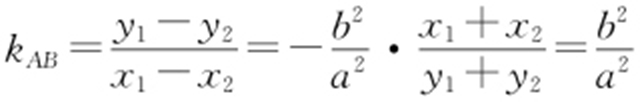 ,
,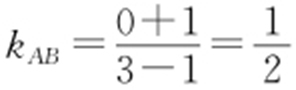 ,所以
,所以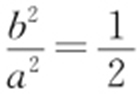 .又9=c 2 =a 2 -b 2 ,解得b 2 =9,a 2 =18,所以椭圆方程
.又9=c 2 =a 2 -b 2 ,解得b 2 =9,a 2 =18,所以椭圆方程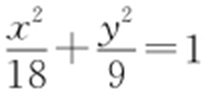 .故选:D.
.故选:D.
【例3 】(2014·安徽理·14) 设F 1 ,F 2 分别是椭圆E :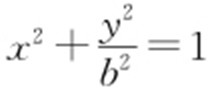 (0<b <1)的左、右焦点,过点F 1 的直线交椭圆E 于A ,B 两点,若|AF 1 |=3|BF 1 |,AF 2 ⊥x 轴,则椭圆E 的方程为 .
(0<b <1)的左、右焦点,过点F 1 的直线交椭圆E 于A ,B 两点,若|AF 1 |=3|BF 1 |,AF 2 ⊥x 轴,则椭圆E 的方程为 .
条件 求出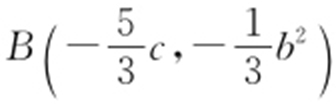 ,代入椭圆方程,结合1=b 2 +c 2 ,即可求出椭圆的方程.
,代入椭圆方程,结合1=b 2 +c 2 ,即可求出椭圆的方程.
解析 由题意,AF 2 ⊥x 轴,所以|AF 2 |=b 2 ,|AF 1 |=3|F 1 B |,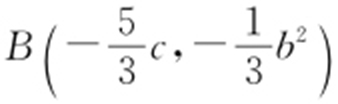 ,代入椭圆方程,得
,代入椭圆方程,得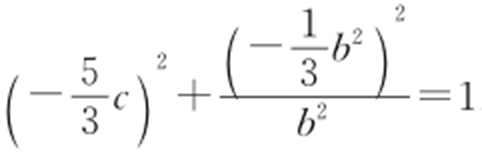 .
.
因为1=b 2 +c 2 ,所以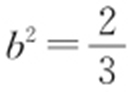 ,
,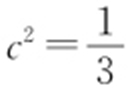 ,
,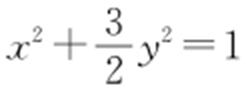 .故答案为
.故答案为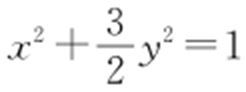 .
.
总结
求椭圆的方程,需要掌握椭圆的方程与性质,以及计算能力.求出a ,b 之后,还要注意焦点位置所在.
练习
1.(2011·新课标理·14) 在平面直角坐标系xOy 中,椭圆C 的中心为原点,焦点F 1 ,F 2 在x 轴上,离心率为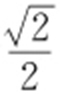 .过点F 1 的直线l 交C 于A ,B 两点,且△ABF 2 的周长为16,那么C 的方程为 .
.过点F 1 的直线l 交C 于A ,B 两点,且△ABF 2 的周长为16,那么C 的方程为 .
2.(2012·大纲理·3改编) 椭圆的中心在原点,焦距为4,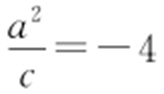 ,则该椭圆的方程为( ).
,则该椭圆的方程为( ).
3.(2013·大纲文·8) 已知F 1 (-1,0),F 2 (1,0)是椭圆C 的两个焦点,过F 2 且垂直于x 轴的直线交于A ,B 两点,且|AB |=3,则C 的方程为( ).
考点3 Ax 2 +By 2 =C (A ,B ,C 均不为零)是表示椭圆的条件
例题
【例1 】(2015·内蒙古模考) 若方程x 2 +ky 2 =2表示焦点在y 轴上的椭圆,那么实数k 的取值范围是( ).
A.(0,+∞)
B.(0,2)
C.(1,+∞)
D.(0,1)
条件 Ax 2 +By 2 =C 表示椭圆的条件:
解析 因为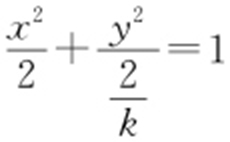 表示焦点在y 轴的椭圆,所以
表示焦点在y 轴的椭圆,所以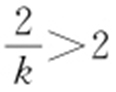 ,故0<k <1.故选:D.
,故0<k <1.故选:D.
【例2 】(2014·合肥模考) 已知方程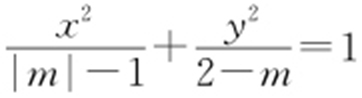 表示焦点在y 轴上的椭圆,则m 的取值范围为 .
表示焦点在y 轴上的椭圆,则m 的取值范围为 .
条件 Ax 2 +By 2 =C 表示焦点在y 轴上的椭圆: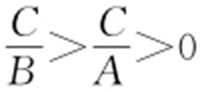 .
.
解析 因为方程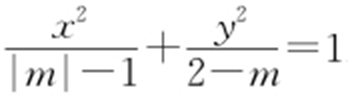 .表示焦点在y 轴上的椭圆,所以2-m >|m |-1>0,解之得
.表示焦点在y 轴上的椭圆,所以2-m >|m |-1>0,解之得 或m <-1,故答案为
或m <-1,故答案为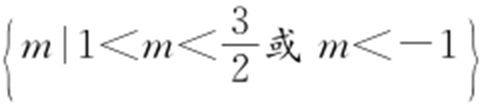 .
.
总结
.
若焦点在x 轴上;
若焦点在y 轴上.
练习
1.(2015·长葛期末) 如果方程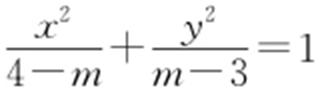 表示焦点在y 轴上的椭圆,则m 的取值范围是( ).
表示焦点在y 轴上的椭圆,则m 的取值范围是( ).
2.(2015·九江期末) 如果方程x 2 -ky 2 =2表示焦点在y 轴上的椭圆,那么实数k 的取值范围是( ).
A.(0,+∞)
B.(0,2)
C.(-1,+∞)
D.(-1,0)
考点4 椭圆中三角形的面积和周长
例题
【例1 】(2016·水富期中) 设M 为椭圆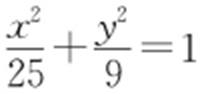 上的一个点,F 1 ,F 2 为焦点,∠F 1 MF 2 =60°,则△MF 1 F 2 的周长和面积分别为( ).
上的一个点,F 1 ,F 2 为焦点,∠F 1 MF 2 =60°,则△MF 1 F 2 的周长和面积分别为( ).
条件 椭圆中焦点三角形面积公式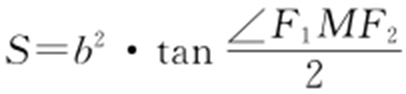 .
.
解析 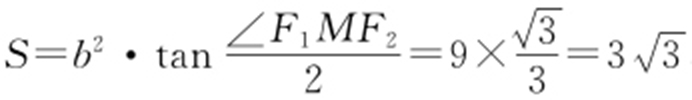 ,周长为18.故选:D.
,周长为18.故选:D.
【例2 】(2016·钦州期末) F 1 ,F 2 分别为椭圆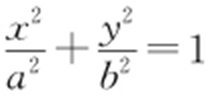 的左、右焦点,点P 在椭圆上,△POF 2 是面积为
的左、右焦点,点P 在椭圆上,△POF 2 是面积为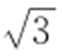 的正三角形,则b 2 的值是 .
的正三角形,则b 2 的值是 .
条件 正三角形 .
.
解析 因为△POF 2 是面积为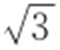 的正三角形,所以
的正三角形,所以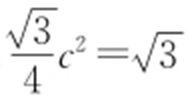 ,解得c =2,则
,解得c =2,则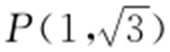 .代入椭圆方程,可得
.代入椭圆方程,可得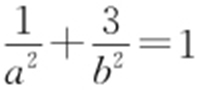 ,与a 2 =b 2 +4联立,得
,与a 2 =b 2 +4联立,得 .
.
【例3 】(2012·四川理·15) 椭圆 的左焦点为F ,直线x =m 与椭圆相交于点A ,B ,当△FAB 的周长最大时,△FAB 的面积是 .
的左焦点为F ,直线x =m 与椭圆相交于点A ,B ,当△FAB 的周长最大时,△FAB 的面积是 .
条件 当△FAB 周长最大时,x =m 与椭圆交于A ,B 两点,|AB |即为通径.
解析 因为当△FAB 周长最大时,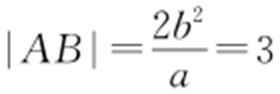 ,
,

【例4 】(2012·四川文·15) 椭圆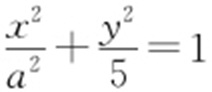 (a 为定值,且
(a 为定值,且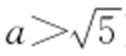 )的左焦点为F ,直线x =m 与椭圆相交于点A ,B ,△FAB 的周长的最大值是12,则该椭圆的离心率是 .
)的左焦点为F ,直线x =m 与椭圆相交于点A ,B ,△FAB 的周长的最大值是12,则该椭圆的离心率是 .
条件 当△FAB 周长最大时,x =m 与椭圆交于A ,B 两点,|AB |即为通径.
解析 因为当△FAB 周长最大时,即为4a =12,a =3,则a 2 =9,c 2 =4,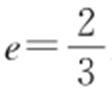 .
.
【例5 】(2016·新课标2理·20) 已知椭圆E : 的焦点在x 轴上,A 是E 的左顶点,斜率为k (k >0)的直线交E 于A ,M 两点,点N 在E 上,MA ⊥NA .当t =4,|AM |=|AN |时,求△AMN 的面积.
的焦点在x 轴上,A 是E 的左顶点,斜率为k (k >0)的直线交E 于A ,M 两点,点N 在E 上,MA ⊥NA .当t =4,|AM |=|AN |时,求△AMN 的面积.
条件 △AMN 面积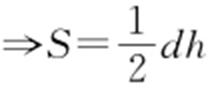 (选合适的顶点或底).
(选合适的顶点或底).
解析 椭圆方程为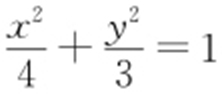 .因为|AM |=|AN |,MA ⊥NA ,又根据椭圆的对称性∠MAF =∠NAF =45°,所以AM 的方程为y =x +2.
.因为|AM |=|AN |,MA ⊥NA ,又根据椭圆的对称性∠MAF =∠NAF =45°,所以AM 的方程为y =x +2.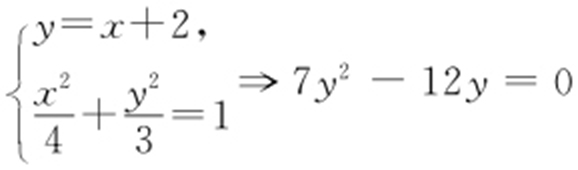 ,
,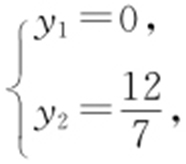 所以M 点的纵坐标为
所以M 点的纵坐标为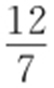 ,则
,则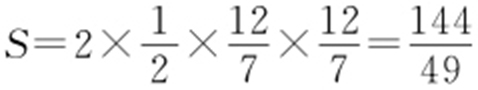 .
.
总结
椭圆中焦点三角形的周长为2a +2c ,面积为.
练习
1.(2016·安徽月考) 设M 是椭圆 上一点,F 1 ,F 2 为焦点,
上一点,F 1 ,F 2 为焦点,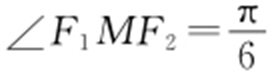 ,则
,则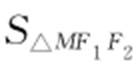 = .
= .
2.(2016·上饶期中) 若点P 在椭圆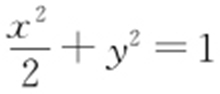 上,F 1 ,F 2 分别是椭圆的两焦点,且∠F 1 PF 2 =60°,则△F 1 PF 2 的面积是( ).
上,F 1 ,F 2 分别是椭圆的两焦点,且∠F 1 PF 2 =60°,则△F 1 PF 2 的面积是( ).
3.(2012·新课标文理·4) 设F 1 ,F 2 是椭圆E :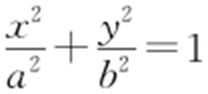 (a >b >0)的左、右焦点,P 为直线
(a >b >0)的左、右焦点,P 为直线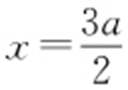 上一点,△F 2 PF 1 是底角为30°的等腰三角形,则E 的离心率为( ).
上一点,△F 2 PF 1 是底角为30°的等腰三角形,则E 的离心率为( ).
4.(2014·大纲文·9) 已知椭圆C :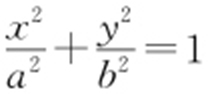 (a >b >0)的左、右焦点为F 1 ,F 2 ,离心率为
(a >b >0)的左、右焦点为F 1 ,F 2 ,离心率为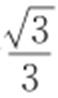 ,过F 2 的直线l 交C 于A ,B 两点,若△AF 1 B 的周长为
,过F 2 的直线l 交C 于A ,B 两点,若△AF 1 B 的周长为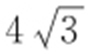 ,则C 的方程为( ).
,则C 的方程为( ).
5.(2014·安徽文·21) 设F 1 ,F 2 分别是椭圆E :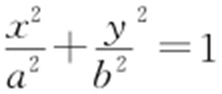 (a >b >0)的左、右焦点,过点F 1 的直线交椭圆E 于A ,B 两点,|AF 1 |=3|BF 1 |.
(a >b >0)的左、右焦点,过点F 1 的直线交椭圆E 于A ,B 两点,|AF 1 |=3|BF 1 |.
若|AB |=4,△ABF 2 的周长为16,求|AF 2 |.
考点5 椭圆上的点到直线的距离最值
例题
【例题 】(2016·钦州期末)设P 是椭圆C :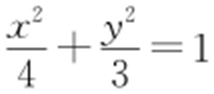 上的动点,则P 到直线
上的动点,则P 到直线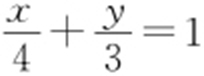 的距离的最小值是( ).
的距离的最小值是( ).
条件 找出与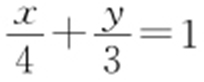 平行且与椭圆相切的直线.
平行且与椭圆相切的直线.
解析 设与3x +4y -12=0平行的直线为3x +4y +c =0.
由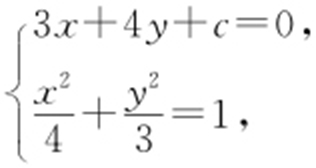 可得32 ×4+42 ×3=c 2 ,
可得32 ×4+42 ×3=c 2 ,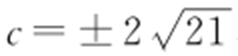 ,可得两条切线方程
,可得两条切线方程 或
或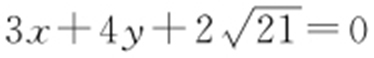 ,即椭圆上的点到直线3x +4y -12=0距离最小值为3x +4y -12=0与
,即椭圆上的点到直线3x +4y -12=0距离最小值为3x +4y -12=0与 的距离,即
的距离,即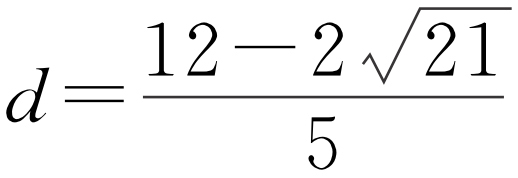 .故选:D.
.故选:D.
总结
直线Ax +By +C =0与椭圆相切的条件:a 2 A 2 +b 2 B 2 =C 2 .
练习
(2013·城厢期中) 设P 为椭圆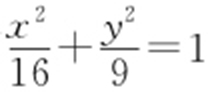 上的动点,则P 到直线x +y -6=0的最小距离为( ).
上的动点,则P 到直线x +y -6=0的最小距离为( ).
考点6 直线斜率
例题
【例1 】(2016·淮南一模) 椭圆C :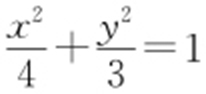 的左、右顶点分别为A 1 ,A 2 ,点P 在C 上,且直线PA 2 斜率的取值范围是[-2,-1],那么直线PA 1 斜率的取值范围是( ).
的左、右顶点分别为A 1 ,A 2 ,点P 在C 上,且直线PA 2 斜率的取值范围是[-2,-1],那么直线PA 1 斜率的取值范围是( ).
条件 找出P 点的坐标,求得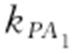 和
和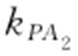 ,以及
,以及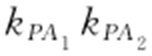 .
.
解析 由椭圆C :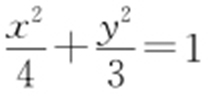 ,可知其左顶点A 1 (-2,0),右顶点A 2 (2,0).设P (x 0 ,y 0 )(x 0 ≠±2),则得
,可知其左顶点A 1 (-2,0),右顶点A 2 (2,0).设P (x 0 ,y 0 )(x 0 ≠±2),则得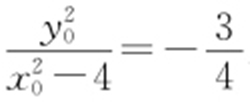 .
.
因为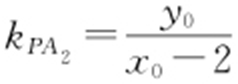 ,
,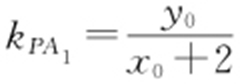 ,所以
,所以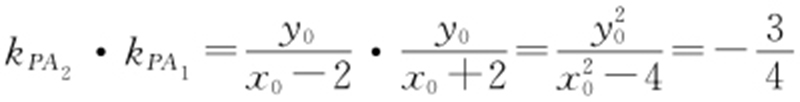 .
.
因为PA 2 的斜率的范围为[-2,-1],所以PA 1 的斜率的范围为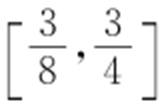 .故选:A.
.故选:A.
【例2 】(2016·衡水一模) 设点A 1 ,A 2 分别为椭圆C :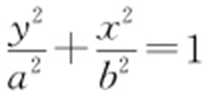 (a >b >0)的下顶点和上顶点,若在椭圆上存在点P 使得
(a >b >0)的下顶点和上顶点,若在椭圆上存在点P 使得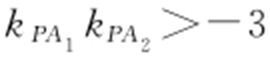 ,则椭圆C 的离心率的取值范围是( ).
,则椭圆C 的离心率的取值范围是( ).
条件 设出P 点坐标,求得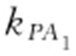 和
和 ,以及
,以及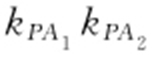 .
.
解析 设P (b sinα ,a cosα ),A 1 (0,-a ),A 2 (0,a ),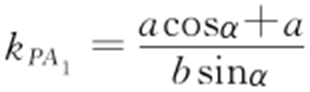 ,
, ,
,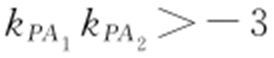 ,得
,得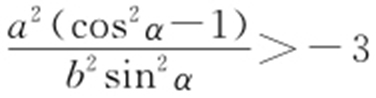 ,即
,即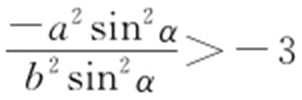 ,
,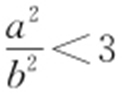 ,
,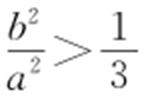 ,
, ,故
,故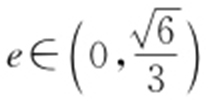 .故选:B.
.故选:B.
总结
掌握椭圆的标准方程及其性质和斜率的计算公式,不等式的性质是解题的关键.
练习
1.(2016·白山一模) P 为椭圆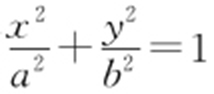 (a >b >0)上异于左右顶点A 1 ,A 2 的任意一点,则直线PA 1 与PA 2 的斜率之积为定值
(a >b >0)上异于左右顶点A 1 ,A 2 的任意一点,则直线PA 1 与PA 2 的斜率之积为定值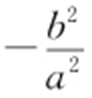 ,将这个结论类比到双曲线,得出的结论为:P 为双曲线
,将这个结论类比到双曲线,得出的结论为:P 为双曲线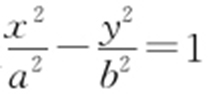 (a >0,b >0)上异于左右顶点A 1 ,A 2 的任意一点,则( ).
(a >0,b >0)上异于左右顶点A 1 ,A 2 的任意一点,则( ).
2.(2016·河南模拟) 设点A 1 ,A 2 分别为椭圆C :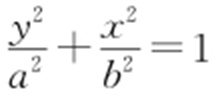 (a >b >0)的下顶点和上顶点,若在椭圆上存在点P 使得
(a >b >0)的下顶点和上顶点,若在椭圆上存在点P 使得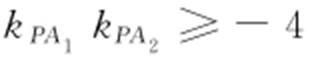 ,则椭圆C 的离心率的取值范围是 .
,则椭圆C 的离心率的取值范围是 .
考试分数高的因素有很多,不是简单地上课认真就能拥有好的成绩.
——冷冷的隆兄(袁龙老师)
一个段子说“我”去买烟,买了一包20元的烟,给老板50元钱,老板找“我”40元,我假装没注意,装兜里就走了.
——博哥说故事 坦诚(1)
没走多远,老板喊:“小伙子,你的烟没拿!”我于是流下了感动的泪水,良心发现,拿出10元钱给老板,说:“你多找了我10元钱.”
——博哥说故事 坦诚(2)
老板也流下了感动的泪水:“小伙子把烟拿回来,我给你换一包真的吧.”
——博哥说故事 坦诚(3)
抽着老板新换给我的烟,那纯正的味道不禁再次感动了我,我说:“老板,把刚才那张50元拿来,我也给你换张真的吧.”
——博哥说故事 坦诚(4)
让你耀眼的,不是别人.只能是你自己.
——博哥(梁立博老师)
如果一个理发师他的顾客集合是那些不会帮自己理发的人,那么请问他是不是这个集合中的元素?
——邵爷(邵菁璟老师)
传说中的笛卡儿心形线,用极坐标来表达,水平方向或
(a >0),垂直方向
或
(a >0),这是大学学霸的表白神器.
——邵爷(邵菁璟老师)
不会空间分析,以后陪老婆逛商场你都找不到出口,立体几何太差的男生要加油.
——邵爷(邵菁璟老师)
在你还没有接受教育时就已经会计算买促销零食的最优解了,然而现在把这些转化成数学你却懵了!
——邵爷(邵菁璟老师)
每当我用很牛的方法计算向我父亲证明他打牌输赢的概率是个会趋于持平的时候,他一次次地打我脸,这个悲伤的故事告诉我,理想环境下的概率计算,用在现实生活中,认真你就被打脸!
——邵爷(邵菁璟老师)
不要让现在的自己成为零向量,目标大学、方向任意,知识储备的大小却为零.
——邵爷(邵菁璟老师)
当你在大海中遇险时,你可以静静地拿出纸笔,计算靠你最近的船只按它的航行速度多久才能救到你,但前提是你得先联系上它.
——邵爷(邵菁璟老师)















