第6章 解析几何大题
直线与圆锥曲线相交时的弦长问题是一个难点,化解这个难点的方法是:设而不求,根据根与系数的关系,进行整体代入.即当直线(斜率为k )与圆锥曲线交于点A (x 1 ,y 1 ),B (x 2 ,y 2 )时,则
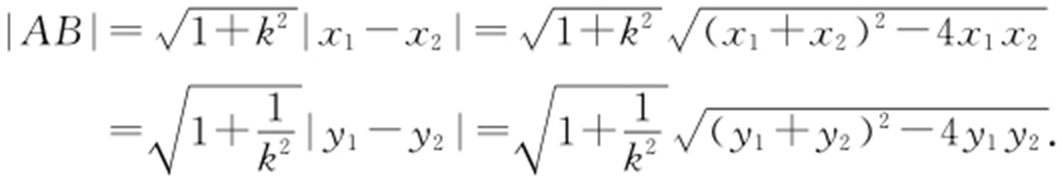
解析几何大题条件转化综合:
(1)以弦AB 为直径的圆过点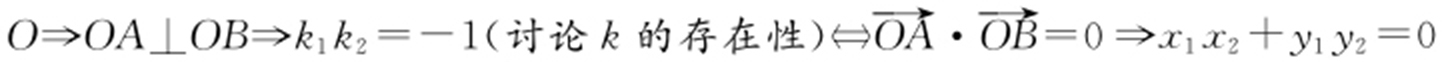 .
.
(2)点在圆上、圆外、圆内问题⇒直角、锐角、钝角问题⇒向量数量积大于、等于、小于0问题.
(3)等角、角平分、角互补问题⇔k 1 +k 2 =0或k 1 =k 2 .
(4)向量比例、共线问题⇔坐标表示法.
(5)点、线对称⇔坐标与斜率关系.
(6)弦长与面积⇒点与线距离、弦长公式.
(7)定点(线)问题⇒从特殊到一般的证明思路.
考点1 轨迹方程的求法
方法1 定义法
例题
【例1 】(2013·新课标1理·20) 已知圆M :(x +1)2 +y 2 =1,圆N :(x -1)2 +y 2 =9,动圆P 与M 外切并且与圆N 内切,圆心P 的轨迹为曲线C ,求C 的方程.
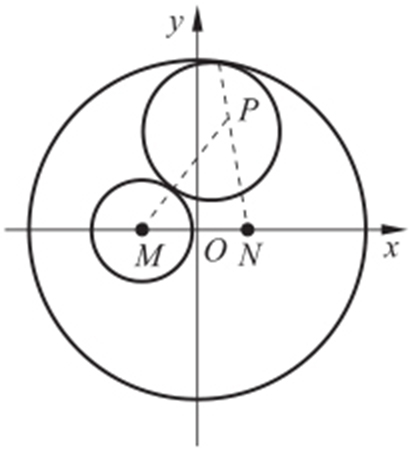
条件 内切⇒|O 1 O 2 |=|r 1 -r 2 |,外切⇒|O 1 O 2 |=|r 1 +r 2 |.
解析 如图.设圆P 的半径为r (变量),|PM |=r +1,|PN |=3-r ,所以消变量r ⇒|PM |+|PN |=4>2(MN ).所以P 的轨迹为椭圆,故方程为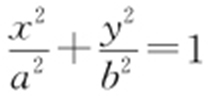 .
.
2a =4⇒a =2,2c =2⇒c =1,所以b 2 =3,即轨迹方程为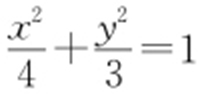 .
.
【例2 】(2014·湖北文·22) 在平面直角坐标系xOy 中,点M 到点F (1,0)的距离比它到y 轴的距离多1.记点M 的轨迹为C .求轨迹C 的方程.
条件 点点距与点线距的关系⇒抛物线的定义.
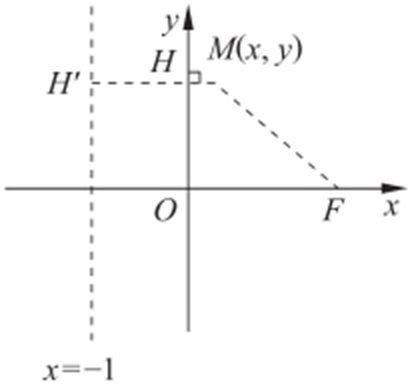
解析 设M (x ,y ).
(1)当x ≥0时,MF =MH +1,延伸至x =-1,可知MF =MH′ ,故M 的轨迹为抛物线,所以方程为y 2 =2px .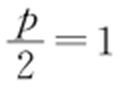 ,p =2,故为y 2 =4x (x ≥0).
,p =2,故为y 2 =4x (x ≥0).
(2)当x <0时,y =0上的点可以满足条件,故轨迹方程为y 2 =4x (x ≥0)或y =0(x <0).
总结
定义法必须熟悉四种曲线(圆、椭圆、双曲线、抛物线)的概念.
定义法步骤:判断定义⇒设轨迹方程⇒待定系数.
练习
1.(2011·广东理·19)设圆C 与两圆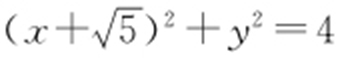 ,
,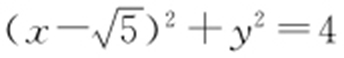 中的一个内切,另一个外切.求C 的圆心轨迹L 的方程.
中的一个内切,另一个外切.求C 的圆心轨迹L 的方程.
2.(2010·江门模考) 设动点P (x ,y )(x ≥0)到定点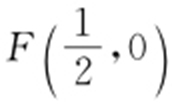 的距离比它到y 轴的距离大
的距离比它到y 轴的距离大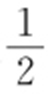 ,记点P 的轨迹为曲线C ,求点P 的轨迹方程.
,记点P 的轨迹为曲线C ,求点P 的轨迹方程.
方法2 相关关系法
例题
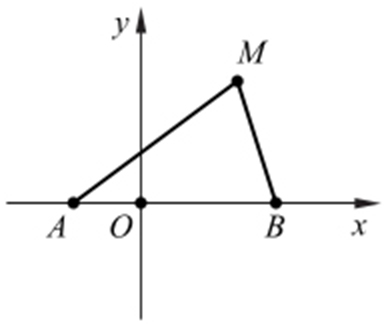
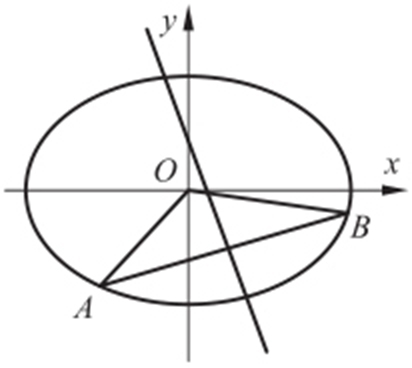
【例 】(2012·四川文理·21) 如图,动点M 到两定点A (-1,0),B (2,0)构成△MAB ,且∠MBA =2∠MAB ,设动点M 的轨迹为C .求轨迹C 的方程.
条件 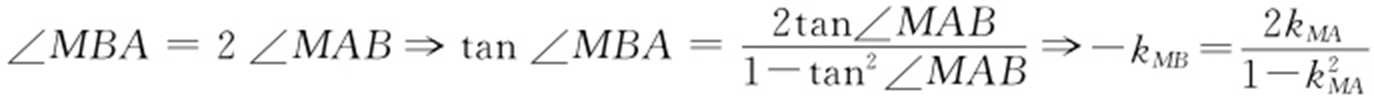 .
.
(角度⇒斜率).
解析 设M (x ,y ),由题意可知x >0.
①当∠MBA =90°时,M (2,±3).
②当∠MBA ≠90°时,
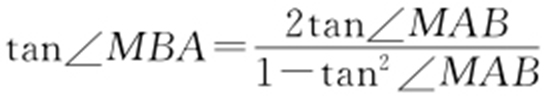 ,则
,则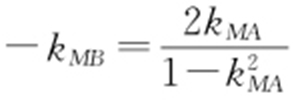 ,
,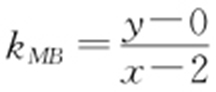 ,
,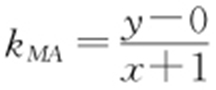 ,所以
,所以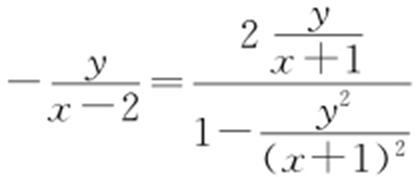 ,所以3x 2 -y 2 -3=0(x >1).
,所以3x 2 -y 2 -3=0(x >1).
经验证,M (2,±3)也在此轨迹上,故M 的轨迹方程为3x 2 -y 2 -3=0(x >1).
总结
(1)解析几何中的角度关系需转化成直线斜率,注意考虑斜率的存在问题.
(2)相关关系法即将题中条件转化成与之有关的关系方程.
练习
1.(2013·陕西文·20) 已知动点M (x ,y )到直线l :x =4的距离是它到点N (1,0)的距离的2倍.求动点M 的轨迹C 的方程.
2.(2013·陕西理·20) 已知动圆过定点A (4,0),且在y 轴上截得的弦MN 的长为8.求动圆圆心的轨迹C 的方程.
方法3 相关点法
例题
【例 】(2011·陕西理·17) 如图,设P 是圆x 2 +y 2 =25上的动点,点D 是P 在x 轴上的投影,M 为PD 上一点,且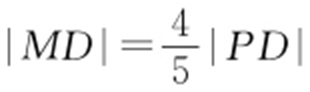 ,当P 在圆上运动时,求点M 的轨迹C 的方程.
,当P 在圆上运动时,求点M 的轨迹C 的方程.
条件 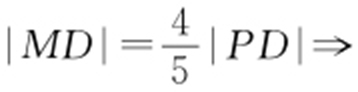 将M 的坐标转化成P 的坐标.
将M 的坐标转化成P 的坐标.

解析 设M 的坐标为M (x ,y ),P 的坐标为P (x 0 ,y 0 ),由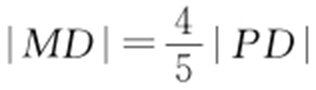 ,可知x =x 0 ,且
,可知x =x 0 ,且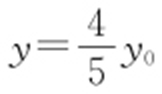 .而P 点在圆上,故
.而P 点在圆上,故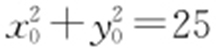 ,所以利用x 0 =x ,
,所以利用x 0 =x ,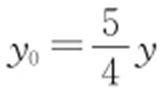 代入可知:
代入可知: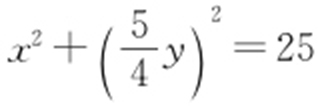 ,即
,即 .
.
总结
(1)相关点法与相关关系法的区别在于相关点题中必有一个动点是有轨迹方程的.
(2)点坐标转化时可尽量利用向量关系.
练习
(2013·上海模考) 已知抛物线C :y 2 =4x 的焦点为F ,点A ,P 满足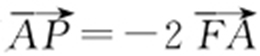 .当点A 在抛物线C 上运动时,求动点P 的轨迹方程.
.当点A 在抛物线C 上运动时,求动点P 的轨迹方程.
方法4 消参法
例题
【例 】(2017·东山月考) 在直角坐标系xOy 上取两个定点A 1 (-2,0),A 2 (2,0),再取两个动点N 1 (0,m ),N 2 (0,n ),且mn =3,求直线A 1 N 1 和A 2 N 2 交点的轨迹M 的方程.
条件 m ·n =3⇒M (x ,y )坐标转化成参数m ,n .
解析 两直线方程可设为AN 1 :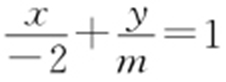 ,AN 2 :
,AN 2 :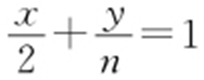 .
.
方法1:联立可得交点M (x ,y )的坐标: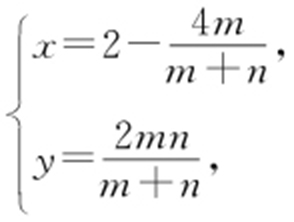 消参可得:
消参可得: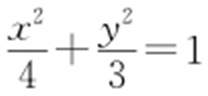 .
.
方法2:点M (x ,y )在AN 1 ,AN 2 上,即满足AN 1 :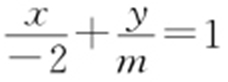 ,AN 2 :
,AN 2 :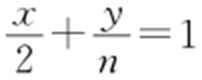 ,又m ·n =3,则
,又m ·n =3,则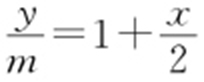 ,
,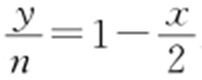 .
.
相乘可得 (x ≠±2).
(x ≠±2).
总结
消参法一般有两种方法:代入消参法(求出参数)(方法1),直接消参法(加减乘除)(方法2).
练习
(2007·武昌期中) 过点M (-2,0),作直线l 交双曲线x 2 -y 2 =1于A ,B 不同两点,已知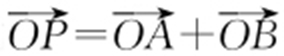 .求点P 的轨迹方程,并说明轨迹是什么曲线.
.求点P 的轨迹方程,并说明轨迹是什么曲线.
考点2 点差法(中点弦公式)
例题
【例1 】(2013·新课标1理·10) 已知椭圆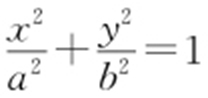 (a >b >0)的右焦点为F (3,0),过点F 的直线交椭圆于A ,B 两点.若AB 的中点坐标为(1,-1),则椭圆的方程为( ).
(a >b >0)的右焦点为F (3,0),过点F 的直线交椭圆于A ,B 两点.若AB 的中点坐标为(1,-1),则椭圆的方程为( ).
条件 (1)点在曲线上⇒点坐标满足曲线方程.
(2)曲线方程+中点+斜率⇒点差法(公式).
解析 设中点坐标C (1,-1),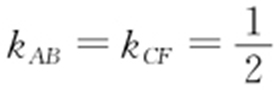 ,设A (x 1 ,y 1 ),B (x 2 ,y 2 ),代入椭圆中,
,设A (x 1 ,y 1 ),B (x 2 ,y 2 ),代入椭圆中,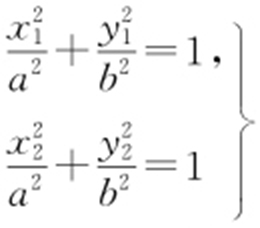 作差得
作差得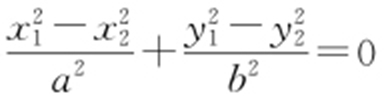 ,整理得
,整理得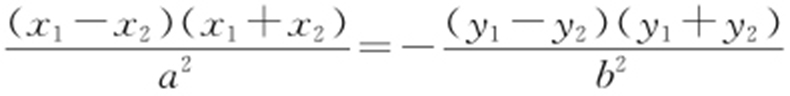 ,
,
则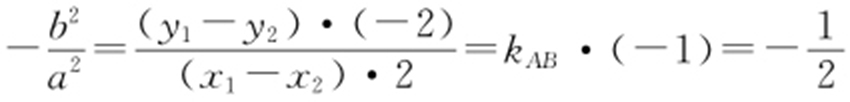 ,
,
即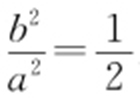 .又c =3⇒a 2 =18,b 2 =9,所以
.又c =3⇒a 2 =18,b 2 =9,所以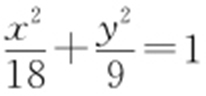 .故选:D.
.故选:D.
【例2 】(2014·江西理·15) 过点M (1,1)作斜率为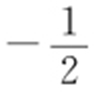 的直线与椭圆C :
的直线与椭圆C :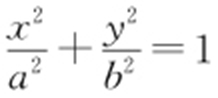 (a >b >0)相交于A ,B ,若M 是线段AB 的中点,则椭圆C 的离心率为 .
(a >b >0)相交于A ,B ,若M 是线段AB 的中点,则椭圆C 的离心率为 .
条件 (1)点在曲线上⇒点坐标满足曲线方程.
(2)曲线方程+中点+斜率⇒点差法(公式).
解析 由题意可得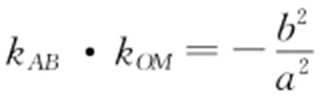 ,所以
,所以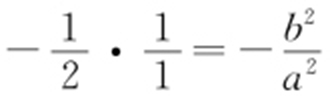 ,则
,则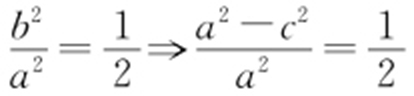 ,即
,即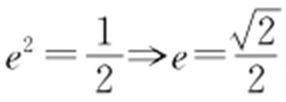 .
.
总结
(1)点差法的标配:曲线方程(离心率、渐近线方程)+中点+弦斜率.
(2)步骤:代点+作差+整理斜率.
(3)公式:已知:曲线、弦AB 、原点O (0,0)、弦中点M (x 0 ,y 0 ),则
.
练习
(2013·新课标2理·20) 平面直角坐标系xOy 中,过椭圆M :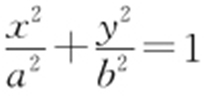 (a >b >0)右焦点的直线
(a >b >0)右焦点的直线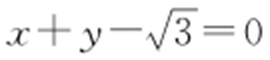 交M 于A ,B 两点,P 为AB 的中点,且OP 的斜率为
交M 于A ,B 两点,P 为AB 的中点,且OP 的斜率为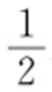 .求M 的方程.
.求M 的方程.
考点3 弦长公式
例题
【例1 】(2014·新课标1·20) 已知点A (0,-2),椭圆E :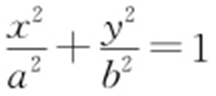 (a >b >0)的离心率为
(a >b >0)的离心率为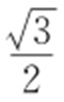 ,F 是椭圆E 的右焦点,直线AF 的斜率为
,F 是椭圆E 的右焦点,直线AF 的斜率为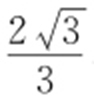 ,O 为坐标原点.
,O 为坐标原点.
(1)求E 的方程;
(2)设过点A 的动直线l 与E 相交于P ,Q 两点,当△OPQ 的面积最大时,求l 的方程.
条件 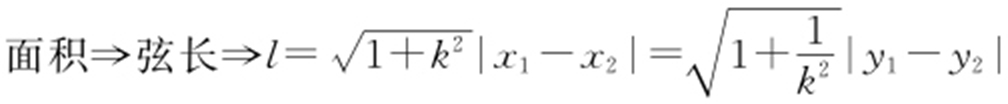 .
.
解析 (1)F (c ,0),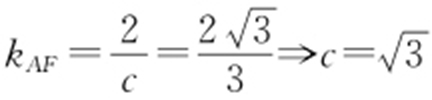 .
.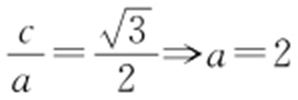 ,b 2 =1,
,b 2 =1,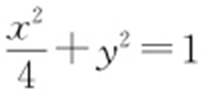 .
.
(2)①当k 不存在时:l :x =0,S △OPQ =0.
②当k 存在时,l :y =kx -2⇒kx -y -2=0.
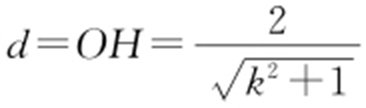 ,
, ,
,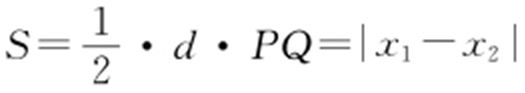 ,
,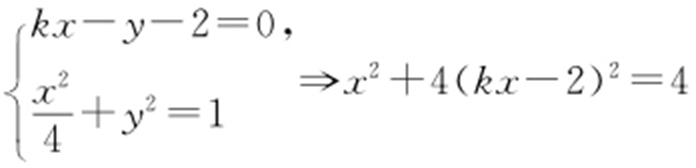 ,
,
即(1+4k 2 )x 2 -16kx +12=0,则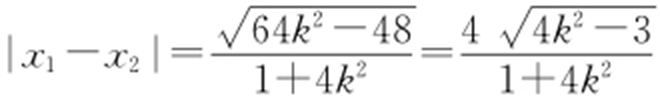 .令
.令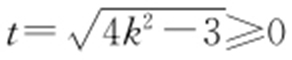 ,则
,则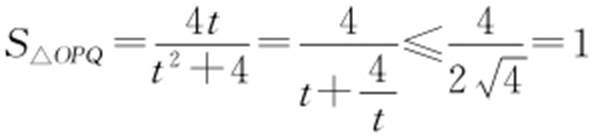 ,此时t =2,即
,此时t =2,即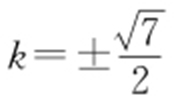 ,此时l :
,此时l :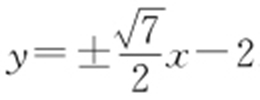 .
.
【例2 】(2013·新课标2理) 平面直角坐标系xOy 中,过椭圆M :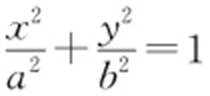 (a >b >0)的右焦点F 作直线
(a >b >0)的右焦点F 作直线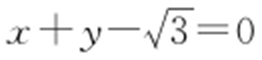 交M 于A ,B 两点,P 为AB 的中点,且OP 的斜率为
交M 于A ,B 两点,P 为AB 的中点,且OP 的斜率为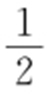 .
.
(1)求M 的方程;
(2)C ,D 为M 上的两点,若四边形ABCD 的对角线CD ⊥AB ,求四边形ABCD 面积的最大值.
条件 (1)方程+中点+斜率⇒点差法(中点弦公式).
(2)四边形对角线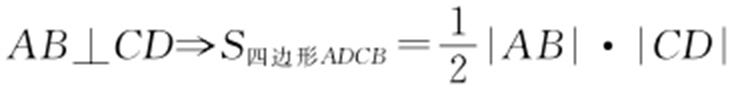 .
.
解析 (点差法)(1)F (c ,0)代入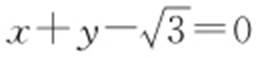 中,
中,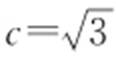 .
.
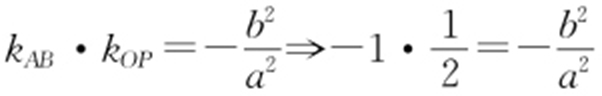 ,所以
,所以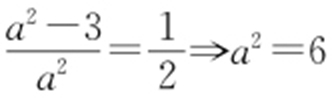 ,b 2 =3,则M 的方程为
,b 2 =3,则M 的方程为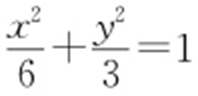 .
.
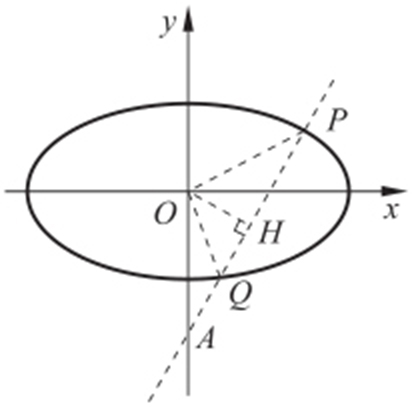
(2)如图:因为CD ⊥AB ,所以CD :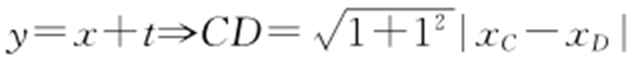 .
.
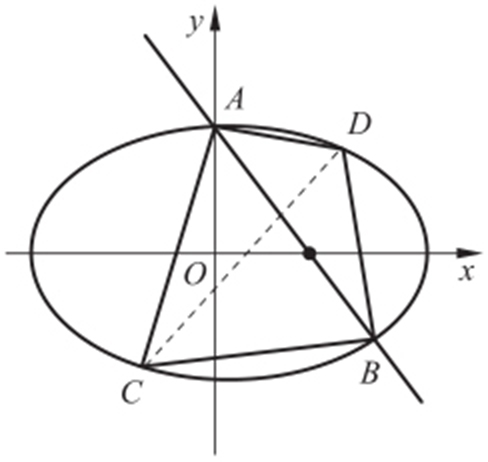
联立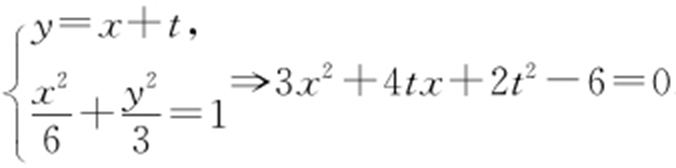 .
.
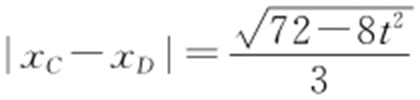 ,72-8t 2 >0⇒-3<t <3,则
,72-8t 2 >0⇒-3<t <3,则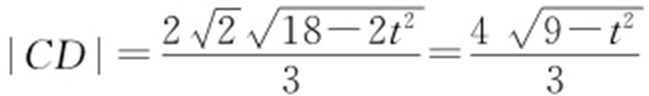 .
.
同理,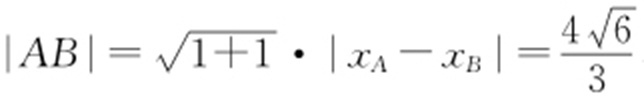 ,则
,则 .又-3<t <3,故
.又-3<t <3,故 ,此时t =0,即
,此时t =0,即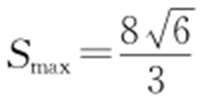 .
.
总结
(1)直线与曲线相交所得弦长.
(2)常用的环境为弦长或面积问题.
练习
(2015·浙江理·19) 已知椭圆 上两个不同的点A ,B 关于直线
上两个不同的点A ,B 关于直线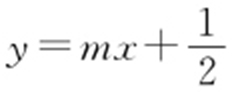 对称.
对称.
(1)求实数m 的取值范围;
(2)求△AOB 面积的最大值(O 为坐标原点).
考点4 向量相关问题
例题
【例1 】(2015·新课标2理·20) 已知椭圆C :9x 2 +y 2 =m 2 (m >0),直线l 不过原点O 且不平行于坐标轴,l 与C 有两个交点A ,B ,线段AB 的中点为M .
(1)证明:直线OM 的斜率与l 的斜率的乘积为定值;
(2)若l 过点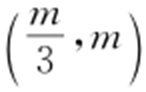 ,延长线段OM 与C 交于点P ,四边形OAPB 能否为平行四边形?若能,求此时l 的斜率;若不能,说明理由.
,延长线段OM 与C 交于点P ,四边形OAPB 能否为平行四边形?若能,求此时l 的斜率;若不能,说明理由.
条件 (1)方程+中点+斜率⇒点差法.
(2)平行四边形⇒向量的加法则:平行四边形法则.
解析 (1)略.k OM ·k l =-9.
(2)假设OAPB 为平行四边形,可得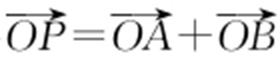 .
.
可设A (x 1 ,y 1 ),B (x 2 ,y 2 ),P (x 0 ,y 0 ),则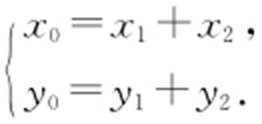 设l :
设l :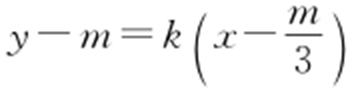 ,即
,即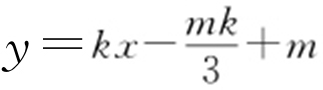 ,联立
,联立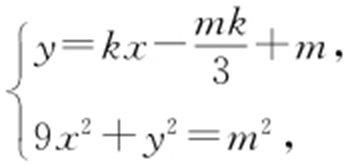 可得
可得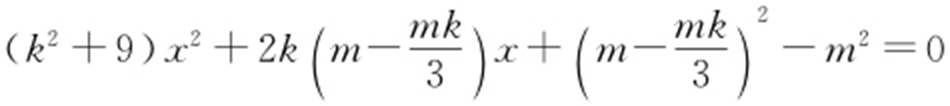 ,
,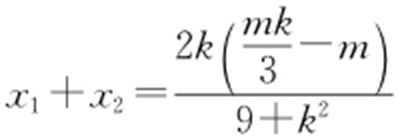 ,
,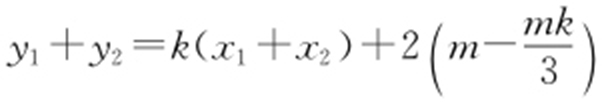 ,故
,故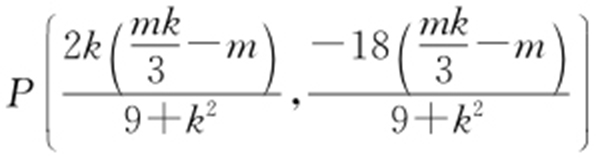 ,代入9x 2 +y 2 =m 2 ,可得
,代入9x 2 +y 2 =m 2 ,可得 时,OAPB 为平行四边形.
时,OAPB 为平行四边形.
【例2 】(2004·黑龙江模考) 给定抛物线C :y 2 =4x ,F 是C 的焦点,过点F 的直线l 与C 相交于A ,B 两点.
(1)设l 的斜率为1,求 与
与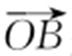 夹角的余弦值;
夹角的余弦值;
(2)设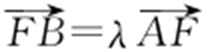 ,若λ ∈[4,9],求l 在y 轴上截距的变化范围.
,若λ ∈[4,9],求l 在y 轴上截距的变化范围.
条件 (1)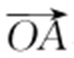 与
与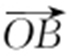 的夹角
的夹角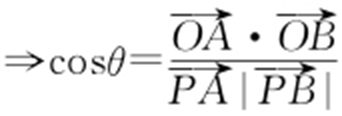 .
.
(2)向量比例⇒坐标比例.
解析 (1)F (1,0),l :y =x -1,设A (x 1 ,y 1 ),B (x 2 ,y 2 ),
联立
.
(2)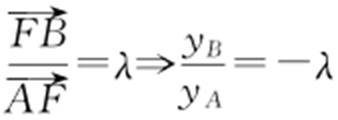 .
.
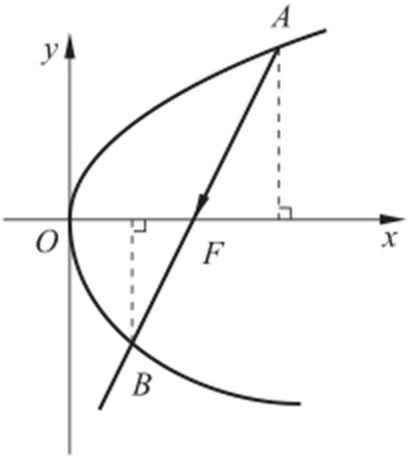
设l :y =k (x -1),即求-k 的取值范围.
因为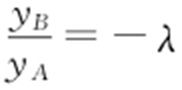 ,则
,则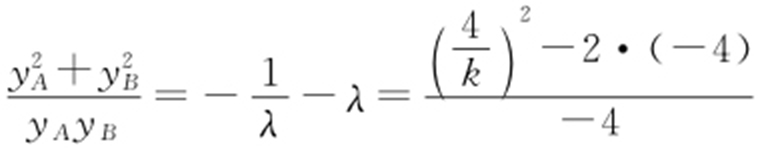 ,所以
,所以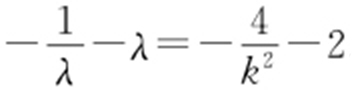 .
.
又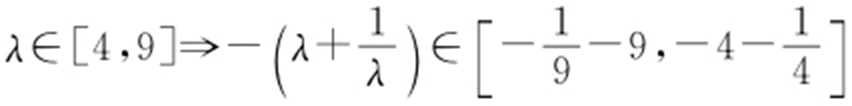 ,所以
,所以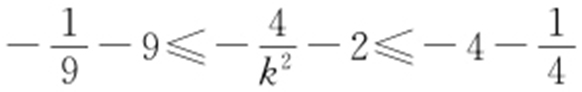 ,即
,即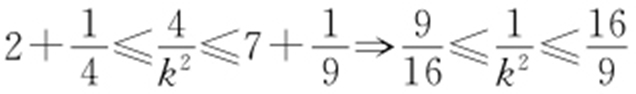 ,从而
,从而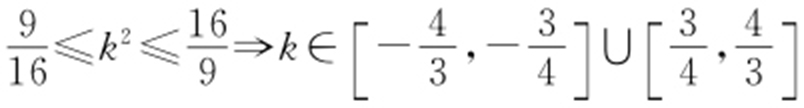 ,故y 轴截距
,故y 轴截距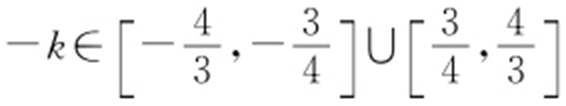 .
.
总结
向量问题尽可能转化为坐标关系:
(1)平行四边形转化成向量加法.
(2)线段之比转化为坐标之比,利用韦达定理.
练习
1.(2013·银川模考) 已知点M (-1,0),N (1,0),动点P (x ,y ),满足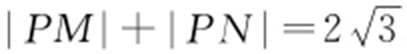 .
.
(1)求点P 的轨迹方程.
(2)是否存在过点N (1,0)的直线l 与曲线C 相交于A ,B 两点,并且曲线C 存在点Q ,使得四边形OAQB 为平行四边形?若存在,求出直线l 的方程,若不存在,说明理由.
2.(2011·秦州月考) 已知椭圆C :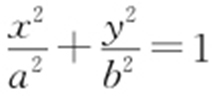 (a >b >0)经过点
(a >b >0)经过点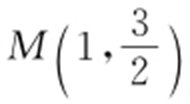 ,其离心率为
,其离心率为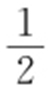 .
.
(1)求椭圆C 的方程.
(2)设直线l :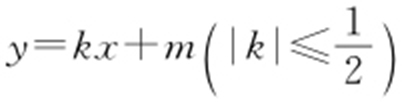 与椭圆C 相交于A ,B 两点,以线段OA ,OB 为邻边作平行四边形OAPB ,其中顶点P 在椭圆C 上,O 为坐标原点.求|OP |的取值范围.
与椭圆C 相交于A ,B 两点,以线段OA ,OB 为邻边作平行四边形OAPB ,其中顶点P 在椭圆C 上,O 为坐标原点.求|OP |的取值范围.
考点5 斜率问题
例题
【例 】(2015·新课标1理·20) 在平面直角坐标系xOy 中,曲线C :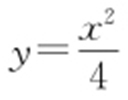 与直线l :y =kx +a (a >0)交于M ,N 两点.
与直线l :y =kx +a (a >0)交于M ,N 两点.
(1)当k =0时,分别求C 在M 点和N 点处的切线方程;
(2)y 轴上是否存在点P ,使得当k 变动时,总有∠OPM =∠OPN ?说明理由.
条件 (1)抛物线x 2 =2py 在其上某点(x 0 ,y 0 )的切线为x 0 x =p (y 0 +y ).
(2)∠OPM =∠OPN ⇒斜率为相反数.
解析 (1)k =0时,l :y =a ,C :x 2 =4y ,此时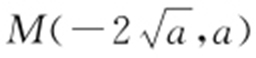 ,
,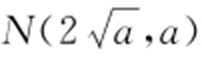 .所以切线方程分别为:
.所以切线方程分别为: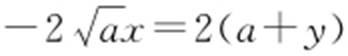 ,
,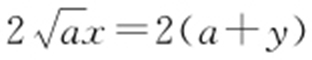 ,即
,即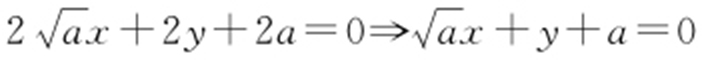 ,
, .
.
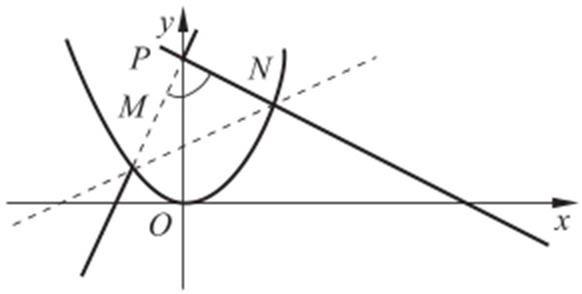
(2)如图,连接PM ,PN 延长交x 轴,可知kPM =tan(90°-∠OPM ),kPN =tan(90°+∠OPN ),所以kPM =-kPN .
设P (0,b ),M (x 1 ,y 1 ),N (x 2 ,y 2 ),即证当kPM =-kPN 时,b 是否为定值?与k 无关?
因为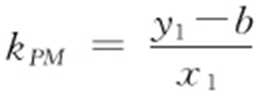 ,
,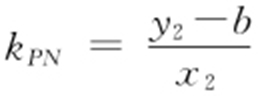 ,则
,则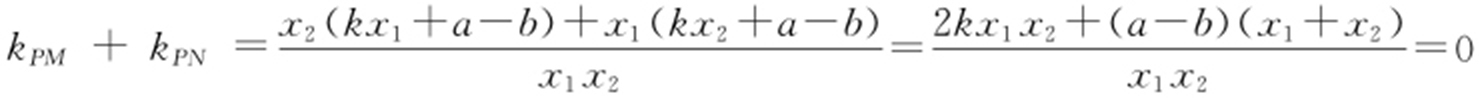 ,
,
联立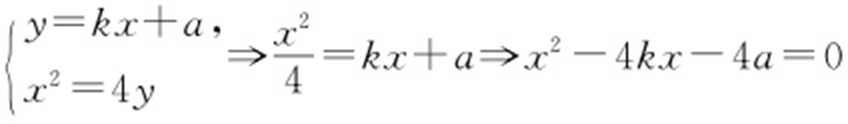 ,x 1 x 2 =-4a ,x 1 +x 2 =4k ,代入①,得-8ka +(a -b )·4k =0⇒k =0或b =-a .
,x 1 x 2 =-4a ,x 1 +x 2 =4k ,代入①,得-8ka +(a -b )·4k =0⇒k =0或b =-a .
所以,当k =0时,任意y 轴上的点均可;当k ≠0时,存在P (0,-a )满足条件.
总结
将条件角度关系转化为斜率再转化为坐标关系,最后使用韦达定理.
练习
(2015·北京理·19) 已知椭圆C :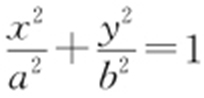 (a >b >0)的离心率为
(a >b >0)的离心率为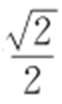 ,点P (0,1)和点A (m ,n )(m ≠0)都在椭圆C 上,直线PA 交x 轴于点M .
,点P (0,1)和点A (m ,n )(m ≠0)都在椭圆C 上,直线PA 交x 轴于点M .
(1)求椭圆C 的方程,并求点M 的坐标(用m ,n 表示);
(2)设O 为原点,点B 与点A 关于x 轴对称,直线PB 交x 轴于点N .问:y 轴上是否存在点Q ,使得∠OQM =∠ONQ ?若存在,求点Q 的坐标;若不存在,说明理由.
考点6 切线问题
例题
【例 】(2014·广东理·20) 已知椭圆C :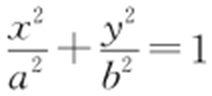 (a >b >0)的一个焦点为
(a >b >0)的一个焦点为 ,离心率为
,离心率为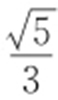 .
.
(1)求椭圆C 的标准方程;
(2)若动点P (x 0 ,y 0 )为椭圆C 外一点,且点P 到椭圆C 的两条切线相互垂直,求点P 的轨迹方程.
条件 直线与曲线相切⇒联立后的二次方程Δ =0.
解析 (1)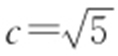 ,
,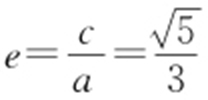 ,a =3,所以b 2 =9-5=4.
,a =3,所以b 2 =9-5=4.
则标准方程为: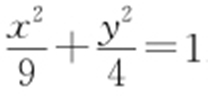 .
.
(2)设切线为l 1 ,l 2 .
①当l 1 ⊥x 轴或l 2 ⊥x 轴时,P (±3,±2).
②当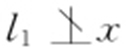 轴或
轴或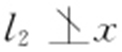 轴时,可设切线为y -y 0 =k (x -x 0 ).
轴时,可设切线为y -y 0 =k (x -x 0 ).
联立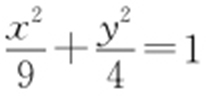 ,有(9k 2 +4)x 2 +18(y 0 -kx 0 )kx +9(y 0 -kx 0 )2 -36=0.
,有(9k 2 +4)x 2 +18(y 0 -kx 0 )kx +9(y 0 -kx 0 )2 -36=0.
令Δ =0,得 .
.
因为方程两根k 1 ·k 2 =-1,所以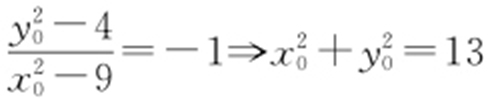 且x 0 ≠±3.
且x 0 ≠±3.
经验证,P (±3,±2)也满足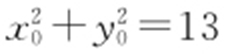 ,故P 的轨迹为x 2 +y 2 =13.
,故P 的轨迹为x 2 +y 2 =13.
总结
(1)直线Ax +By +C =0与曲线相切⇒可转化为A 2 m +B 2 n =C 2 (圆、椭圆、双曲线适用).
(2)过曲线上一点M (x 0 ,y 0 )的切线方程为
,过曲线(y 2 =2px )上一点M (x 0 ,y 0 )的切线方程为y 0 y =p (x 0 +x ).
(3)过曲线外一点M (x 0 ,y 0 )作切线,切点构成切点弦的方程为
.
过曲线y 2 =2px 外一点M (x 0 ,y 0 )作切线,切点构成切点弦的方程为y 0 y =p (x 0 +x ).
练习
(2013·广东理·20) 已知抛物线C 的顶点为原点,其焦点F (0,c )(c >0)到直线l :x -y -2=0的距离为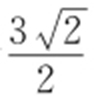 .设P 为直线l 上的点,过点P 作抛物线C 的两条切线PA ,PB ,其中A ,B 为切点.
.设P 为直线l 上的点,过点P 作抛物线C 的两条切线PA ,PB ,其中A ,B 为切点.
(1)求抛物线C 的方程;
(2)当点P (x 0 ,y 0 )为直线l 上的定点时,求直线AB 的方程;
(3)当点P 在直线l 上移动时,求|AF |·|BF |的最小值.
考点7 定点问题
例题
【例1 】(2011·萧山模考) 已知椭圆C 的中心在坐标原点,焦点在x 轴上,椭圆C 上的点到焦点距离的最大值为3,最小值为1.
(1)求椭圆C 的标准方程;
(2)若直线l :y =kx +m 与椭圆C 相交于A ,B 两点(A ,B 不是左右顶点),且以AB 为直径的圆过椭圆C 的右顶点,求证:直线l 过定点,并求出该定点的坐标.
条件 以AB 为直径的圆过右顶点⇒向量数量积为0.
解析 (1)由题意可得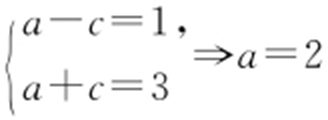 ,c =1,所以椭圆C :
,c =1,所以椭圆C :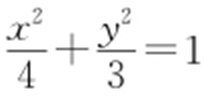 .
.
(2)如图,右顶点C (2,0),A (x 1 ,y 1 ),B (x 2 ,y 2 ),由题意可得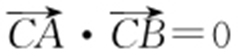 ,即(x 1 -2,y 1 )·(x 2 -2,y 2 )=0,所以
,即(x 1 -2,y 1 )·(x 2 -2,y 2 )=0,所以
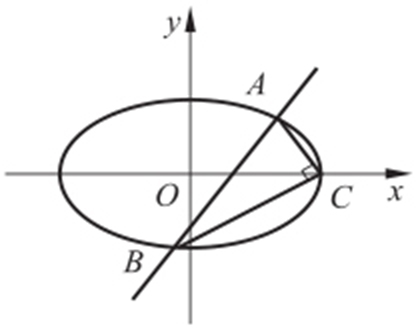
x 1 x 2 -2(x 1 +x 2 )+4+y 1 y 2 =0.
联立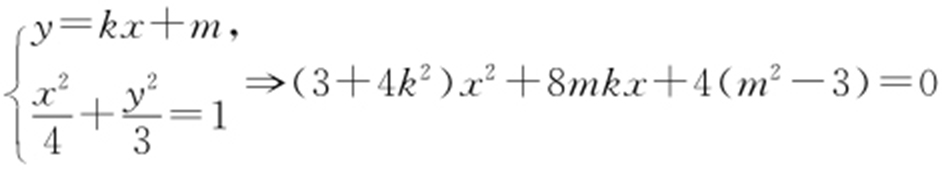 .
.
Δ =64m 2 k 2 -16(3+4k 2 )(m 2 -3)>0,
则3+4k 2 -m 2 >0,所以
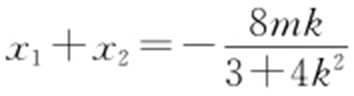 ,
,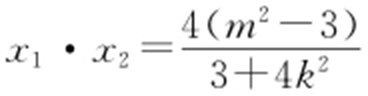 ,
,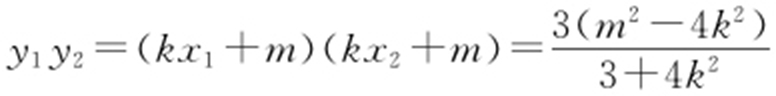 .
.
代入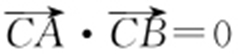 中,有
中,有
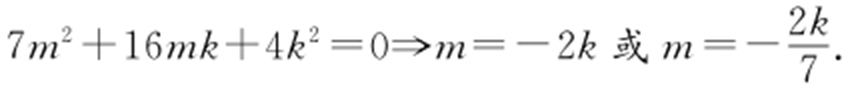
又Δ >0,故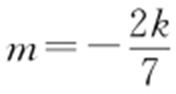 .则l :
.则l :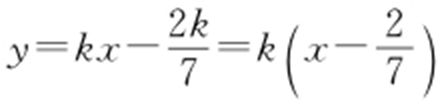 ,故l 过定点
,故l 过定点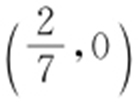 .
.
【例2 】(2013·渝中模考) 已知直线l 1 ,l 2 分别与双曲线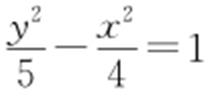 的两条渐近线平行,又与x 轴分别交于M ,N 两点,且满足|OM |2 +|ON |2 =8.
的两条渐近线平行,又与x 轴分别交于M ,N 两点,且满足|OM |2 +|ON |2 =8.
(1)求直线l 1 ,l 2 的交点H 的轨迹E 的方程;
(2)过点S (0,3)作斜率为k 的直线l ,并且l 与轨迹E 交于不同的两点P ,Q ,点R 与点P 关于y 轴对称,证明直线RQ 经过一定点.
条件 |OM |2 +|ON |2 =8⇒消参法求轨迹或相关关系法求轨迹.
解析 (1)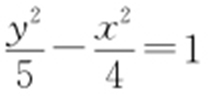 的渐近线为
的渐近线为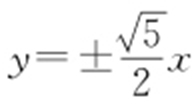 .
.
设M (m ,0),N (n ,0),m 2 +n 2 =8,故l 1 :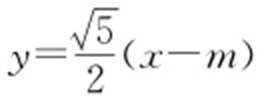 ,l 2 :
,l 2 :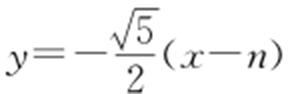 .利用m 2 +n 2 =8,消参可得
.利用m 2 +n 2 =8,消参可得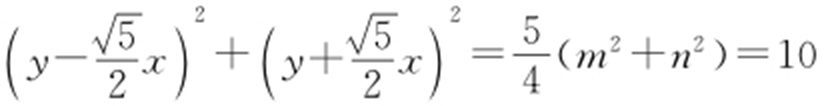 ,所以
,所以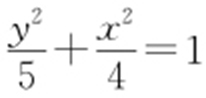 .
.
(2)设QR 与y 轴交于D (0,y 0 ),可知PD 与QR 关于y 轴对称,所以kPD +kQR =0.
设PQ :y =kx +3,设P (x 1 ,y 1 ),Q (x 2 ,y 2 ),R (-x 1 ,y 1 ),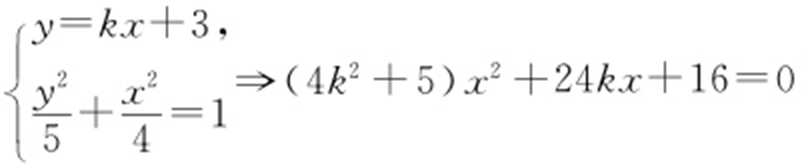 ,则
,则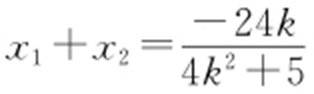 ,
,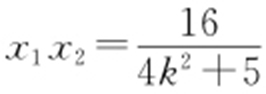 .
.
又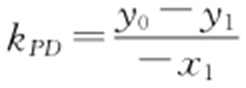 ,
, ,所以
,所以 为
为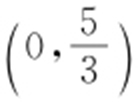 .
.
总结
(1)定点问题必求出定点坐标.
(2)一般有消参的方式和由特殊到一般的两种求法.
练习
(2013·陕西理·20) 已知动圆过定点A (4,0),且在y 轴上截得的弦MN 的长为8.
(1)求动圆圆心的轨迹C 的方程;
(2)已知点B (-1,0),设不垂直于x 轴的直线l 与轨迹C 交于不同的两点P ,Q ,若x 轴是∠PBQ 的角平分线,证明直线l 过定点.
能成为自己想成为的人是莫大的幸福.
——荡荡(曹灏老师)
生活不止当下的沉浸,还有远方的寻觅与心中的诗歌.
——荡荡(曹灏老师)
有的事你真的一点儿都不想去做,但要看这件事是否在推着你的人生往前走,如果是,那就好好去做吧.
——黄文清老师
对于习惯过去的人而言,新的开始其实是很难的,但大家一起起步,改变就会容易很多.
——黄文清老师
梦,是一个一定要谈话的孩子.
——黄文清老师
只要你不在孤单中退缩,不在伤害中沉沦,挫折就会一点点把你武装成你梦想的样子.
——黄文清老师
总是觉得自己被埋没,被委屈,天公不美时运不济,其实是你一直没明白:人,是做出来的,而不是说出来的.做得不好,也只说明了两点:要么实力不够,要么态度敷衍.
——黄文清老师
命运的事情我管不了,它可以随意干它的事,我也可以执着地干自己的事.
——黄文清老师
这个世界上,有的人有路,心却不走,有门,手却不推;而有的人,腿已不便,垂垂老矣,但心依然在奔跑,坚信着梦想与年龄无关.
——黄文清老师
符号我一般都念得还是很标准啊,α阿花,β憋它,γ甲马,δ呆它,ε爱破戏楼.
——江吴清老师
“老师,怎么会有你这样长得那么矮还那么漂亮的人.”
答:“都是一米几的人,说的好像你有两米一样.”
——江吴清老师
一个人的气质里藏着看过的书、走过的路和爱过的人.
——江吴清老师
我中考数学65分,高考数学可以考137分,那么你呢?
——龚敏华老师
在你的全世界路过,只是为了在另一个更加恰当的时机、更美好的环境遇见你.
——龚敏华老师
当你感到绝望时,正是你即将看到黎明的通道时.
——江润涛老师
选择让你驾驭生命,而不是让生命驾驭你.
——江润涛老师
高中三年,看一看字体就知道是谁的卷子,闻一闻气味就知道是谁的衣服.
——江润涛老师
永远不要说你已经尽力了,因为你永远没有办法知道自己的极限.
——江润涛老师
龟兔赛跑的故事告诉你,一旦不努力,你随时可能被超越.
——江润涛老师



