参考答案
第1章 直 线
考点1 直线的倾斜角与斜率
1.B. 2.A.
考点2 直线的五种表达式及位置关系
1.【解析 】 (1)证明:直线l 的方程是:k (x +2)+(1-y )=0,令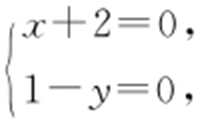 解之得
解之得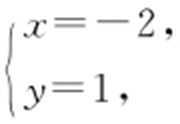 所以无论k 取何值,直线总经过定点(-2,1).
所以无论k 取何值,直线总经过定点(-2,1).
(2)由方程知,当k ≠0时直线在x 轴上的截距为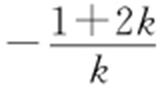 ,在y 轴上的截距为1+2k ,要使直线不经过第四象限,则必须有
,在y 轴上的截距为1+2k ,要使直线不经过第四象限,则必须有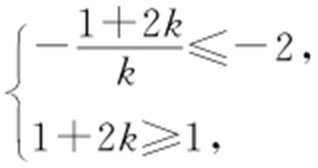 解之得k >0;当k =0时,直线为y =1,符合题意,故k ≥0.
解之得k >0;当k =0时,直线为y =1,符合题意,故k ≥0.
(3)由l 的方程,得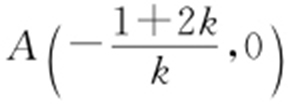 ,B (0,1+2k ).依题意得
,B (0,1+2k ).依题意得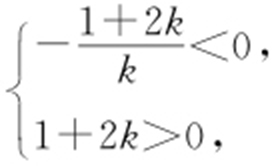 解得k >0.因为
解得k >0.因为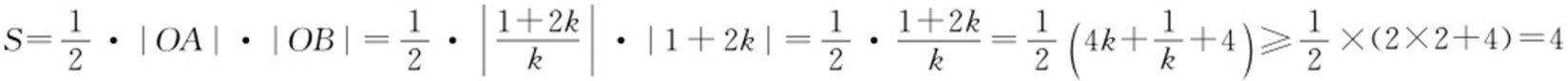 ,“=”成立的条件是k >0且
,“=”成立的条件是k >0且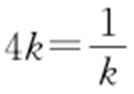 ,即
,即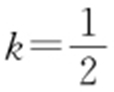 ,所以S min =4,此时l :x -2y +4=0.
,所以S min =4,此时l :x -2y +4=0.
2.B. 3.A. 4.C. 5.C.
考点3 距离和对称
1.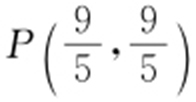 .
.
【解析 】 作点A 关于l 的对称点A′ ,则A′ (3,-3),连接A′B 延长交l 于P ,则||PA |-|PB ||=||PA′ |-|PB ||=|A′B |,所以||PA |-|PB ||最大值为|A′B |,联立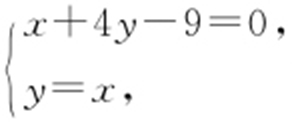 得
得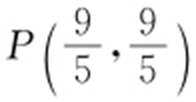 .
.
2.4x +3y +23=0.
【解析 】 设C 关于直线x -y +10=0的对称点为D (a ,b ),则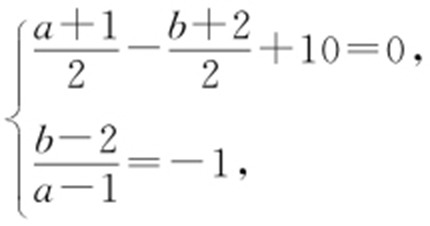 解得
解得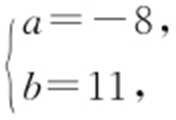 由D (-8,11),可知入射光线所在直线方程为AD 所在直线方程,由直线方程的两点式得
由D (-8,11),可知入射光线所在直线方程为AD 所在直线方程,由直线方程的两点式得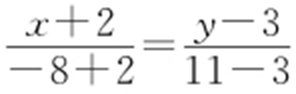 ,即4x +3y +23=0,由两点式求得入射光线所在的直线AC 的方程为 4x +3y +23=0.
,即4x +3y +23=0,由两点式求得入射光线所在的直线AC 的方程为 4x +3y +23=0.
3.x +2y +15=0.
【解析 】 在直线2x +y -3=0上取点A (1,1),A 关于直线x +y +4=0的对称点为A′ ,设A′ (m ,n ),则 解之得A′ (-5,-5).又直线l 1 :2x +y -3=0与直线l 2 :x +y +4=0的交点为B (7,-11),所以直线A′B 的斜率是
解之得A′ (-5,-5).又直线l 1 :2x +y -3=0与直线l 2 :x +y +4=0的交点为B (7,-11),所以直线A′B 的斜率是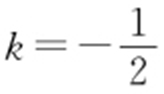 ,所以直线A′B 的方程为x +2y +15=0,即为反射光线所在直线的方程.
,所以直线A′B 的方程为x +2y +15=0,即为反射光线所在直线的方程.
考点4 线性规划
1.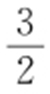 . 2.B. 3.C. 4.216000. 5.C. 6.C. 7.
. 2.B. 3.C. 4.216000. 5.C. 6.C. 7.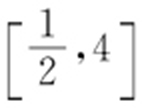 . 8.2或-1. 9.C.
. 8.2或-1. 9.C.
第2章 圆
考点1 圆的方程
1.C. 2.x 2 +(y -1)2 =1. 3.(x -2)2 +y 2 =9.
考点2 直线与圆的位置关系
1.C.
2.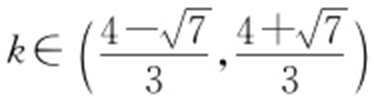 ,|MN |=2.
,|MN |=2.
【解析 】 (1)由题设,可知直线l 的方程为y =kx +1.因为l 与C 交于两点,所以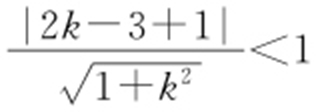 .解得
.解得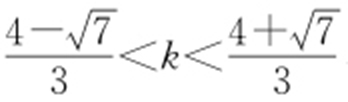 ,所以k 的取值范围为
,所以k 的取值范围为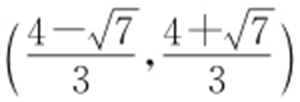 .
.
(2)设M (x 1 ,y 1 ),N (x 2 ,y 2 ).将y =kx +1代入方程(x -2)2 +(y -3)2 =1,整理得 (1+k 2 )x 2 -4(1+k )x +7=0.所以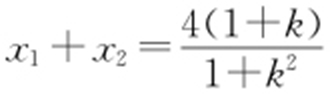 ,
,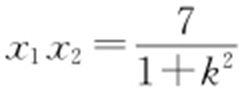 ,
,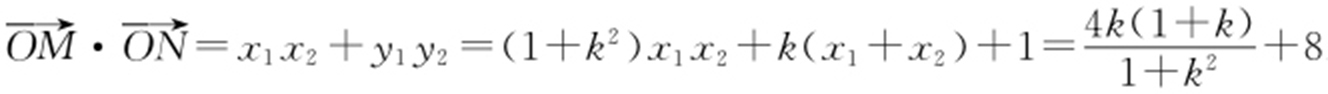 .由题设可得
.由题设可得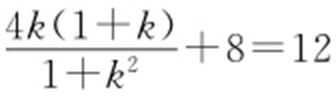 ,解得k =1,所以l 的方程为y =x +1.故圆心C 在l 上,所以|MN |=2.
,解得k =1,所以l 的方程为y =x +1.故圆心C 在l 上,所以|MN |=2.
3.2. 4.B.
考点3 弦长问题
1.C. 2.2. 3.A. 4.4π.
考点4 切线问题
1.D. 2.D. 3.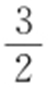 .
.
考点5 圆与圆的位置关系
B.
第3章 椭 圆
考点1 椭圆的定义
1.A.
【解析 】 由题意知,CD 是线段MF 的垂直平分线,所以|MP |=|PF |,所以|PF |+|PO |=|PM |+|PO |=|MO |(定值).又显然|MO |>|FO |,所以根据椭圆的定义可推断出点P 轨迹是以F ,O 两点为焦点的椭圆.
2.C.
【解析 】 因为F 1 (-1,0),F 2 (1,0),所以|F 1 F 2 |=2.因为|F 1 F 2 |是|PF 1 |与|PF 2 |的等差中项,所以2|F 1 F 2 |=|PF 1 |+|PF 2 |,即|PF 1 |+|PF 2 |=4,所以点P 在以F 1 ,F 2 为焦点的椭圆上.又2a =4,a =2,c =1,所以b 2 =3,故椭圆的方程是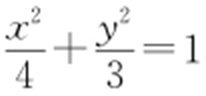 .故选:C.
.故选:C.
考点2 椭圆的方程
1. . 2.C. 3.C.
. 2.C. 3.C.
考点3 Ax 2 +By 2 =C (A ,B ,C 均不为零)是表示椭圆的条件
1.D.
【解析 】 因为方程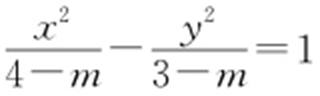 表示焦点在y 轴上的椭圆,所以m -3>4-m >0,则
表示焦点在y 轴上的椭圆,所以m -3>4-m >0,则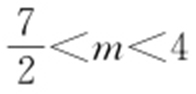 .故选:D.
.故选:D.
2.D.
【解析 】 根据题意,x 2 -ky 2 =2化为标准形式为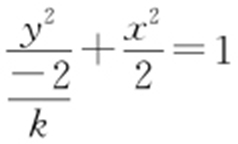 ,根据题意,其表示焦点在y 轴上的椭圆,则有
,根据题意,其表示焦点在y 轴上的椭圆,则有 ,解得-1<k <0.故选:D.
,解得-1<k <0.故选:D.
考点4 椭圆中三角形的面积和周长
1.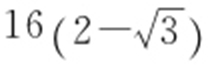 .
.
2.C.
【解析 】 椭圆方程为 ,所以
,所以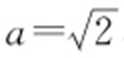 ,b =1,c =1.又P 为椭圆上一点,∠F 1 PF 2 =60°,F 1 ,F 2 为左、右焦点,所以
,b =1,c =1.又P 为椭圆上一点,∠F 1 PF 2 =60°,F 1 ,F 2 为左、右焦点,所以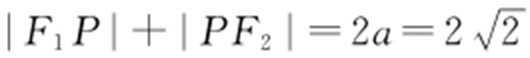 ,|F 1 F 2 |=2c =2,所以|F 1 F 2 |2 =(|PF 1 |+|PF 2 |)2 -2|F 1 P |·|PF 2 |-2|F 1 P |·|PF 2 |cos60°=8-3|F 1 P |·|PF 2 |,所以 8-3|F 1 P |·|PF 2 |=4,即
,|F 1 F 2 |=2c =2,所以|F 1 F 2 |2 =(|PF 1 |+|PF 2 |)2 -2|F 1 P |·|PF 2 |-2|F 1 P |·|PF 2 |cos60°=8-3|F 1 P |·|PF 2 |,所以 8-3|F 1 P |·|PF 2 |=4,即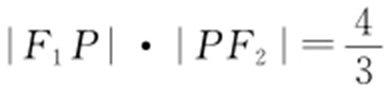 ,则
,则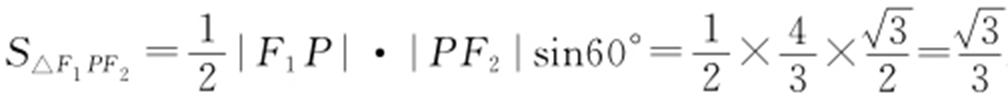 .故选:C.
.故选:C.
3.C.
【解析 】 因为△F 2 PF 1 是底角为30°的等腰三角形,所以|PF 2 |=|F 2 F 1 |.因为P 为直线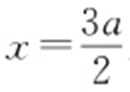 上一点,所以
上一点,所以 ,则
,则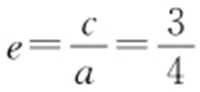 .故选:C.
.故选:C.
4.A.
【解析 】 由椭圆的定义可得,AF 1 +AF 2 =2a ,BF 1 +BF 2 =2a ,又因为 ,所以
,所以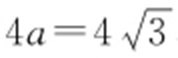 ,解得
,解得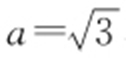 ,又因为
,又因为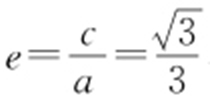 ,所以c =1,b 2 =a 2 -c 2 =2,所以椭圆方程为
,所以c =1,b 2 =a 2 -c 2 =2,所以椭圆方程为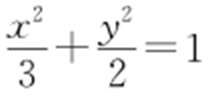 ,故选:A.
,故选:A.
5.|AF 2 |=5.
【解析 】 由|AF 1 |=3|F 1 B |,|AB |=4,得|AF 1 |=3,|F 1 B |=1.因为△ABF 2 的周长为16,所以由椭圆定义可得4a =16,|AF 1 |+|AF 2 |=2a =8,故|AF 2 |=2a -|AF 1 |=8-3=5.
考点5 椭圆上的点到直线的距离最值
C.
【解析 】 设直线x +y -c =0与椭圆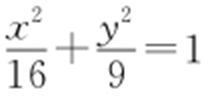 相切,联解消去x ,得25y 2 -18cy +9c 2 -144=0,所以Δ =(-18c )2 -4×25×(9c 2 -144)=0,解之得c =5或c =-5,所以与直线x +y -6=0平行且与椭圆相切的直线方程为x +y ±5=0,其中与直线x +y -6=0距离较近的是x +y -5=0,且距离为
相切,联解消去x ,得25y 2 -18cy +9c 2 -144=0,所以Δ =(-18c )2 -4×25×(9c 2 -144)=0,解之得c =5或c =-5,所以与直线x +y -6=0平行且与椭圆相切的直线方程为x +y ±5=0,其中与直线x +y -6=0距离较近的是x +y -5=0,且距离为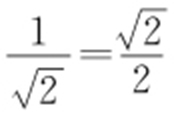 ,故P 到直线x +y -6=0的最小距离为
,故P 到直线x +y -6=0的最小距离为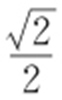 ,故选:C.
,故选:C.
考点6 直线斜率
1.D.
【解析 】 设P (x 0 ,y 0 )为双曲线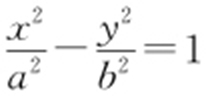 (a >0,b >0)上异于左右顶点A 1 ,A 2 的任意一点,则A 1 (-a ,0),A 2 (a ,0),所以
(a >0,b >0)上异于左右顶点A 1 ,A 2 的任意一点,则A 1 (-a ,0),A 2 (a ,0),所以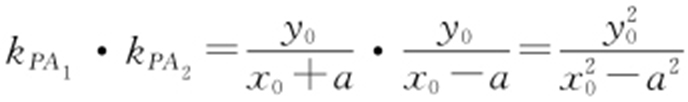 .又P (x 0 ,y 0 )在双曲线
.又P (x 0 ,y 0 )在双曲线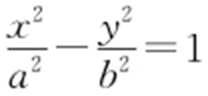 上,所以
上,所以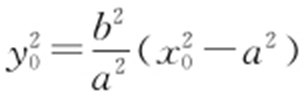 ,则
,则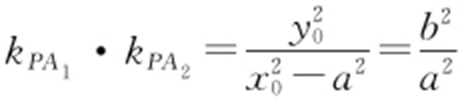 ,所以直线PA 1 与PA 2 的斜率之积为定值
,所以直线PA 1 与PA 2 的斜率之积为定值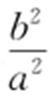 .故选:D.
.故选:D.
2.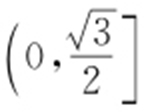 .
.
【解析 】 设P (x 0 ,y 0 ),代入椭圆方程得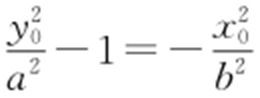 ,即
,即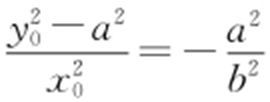 ,又
,又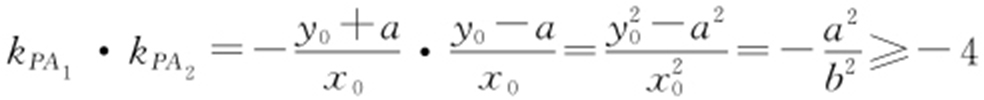 ,所以
,所以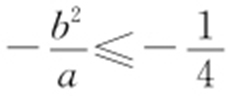 ,即
,即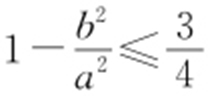 ,所以
,所以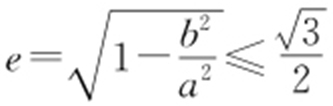 ,即
,即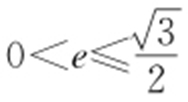 ,故答案为
,故答案为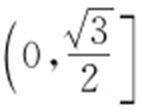 .
.
第4章 双 曲 线
考点1 双曲线的定义
1.A. 2.5.
考点2 双曲线方程
1.16. 2.D.
考点3 双曲线的一般方程
D.
考点4 双曲线的渐近线
1.A. 2.A. 3.C. 4.B.
考点5 焦点三角形与弦心三角形
1.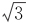 . 2.90°.
. 2.90°.
考点6 椭圆与双曲线综合
1.A. 2.A.
考点7 椭圆与双曲线离心率专题
1.C. 2.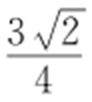 . 3.
. 3.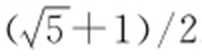 . 4.
. 4.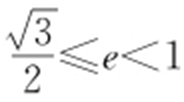 . 5.A.
. 5.A.
第5章 抛 物 线
考点1 抛物线的定义
1.D. 2.D.
考点2 抛物线方程及基本量
x =-2.
考点3 抛物线第一定义
1.C. 2.(2,2).
考点4 抛物线的焦半径和焦点弦性质
1.2. 2.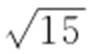 . 3.B. 4.D. 5.
. 3.B. 4.D. 5. .
.
考点5 抛物线与椭圆双曲线综合
1.y =±x . 2.D.
第6章 解析几何大题
考点1 轨迹方程的求法
方法1 定义法
1.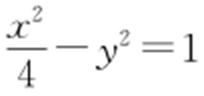 .
.
【解析 】 设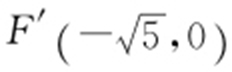 ,
,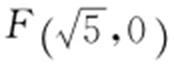 ,并设圆C 的半径为r ,则||CF′ |-|CF ||=|(2+r )-(r -2)|=4.又
,并设圆C 的半径为r ,则||CF′ |-|CF ||=|(2+r )-(r -2)|=4.又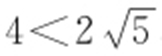 ,则C 的圆心轨迹是以F′ ,F 为焦点的双曲线,且a =2,
,则C 的圆心轨迹是以F′ ,F 为焦点的双曲线,且a =2,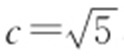 ,从而b =1,则C 的圆心轨迹L 的方程为
,从而b =1,则C 的圆心轨迹L 的方程为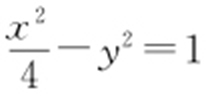 .
.
2.y 2 =2x .
【解析 】 根据题意:点P 到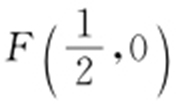 与到直线
与到直线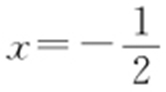 的距离相等,所以点P 的轨迹是抛物线,
的距离相等,所以点P 的轨迹是抛物线,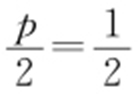 ,p =1,所以轨迹方程为y 2 =2x .
,p =1,所以轨迹方程为y 2 =2x .
方法2 相关关系法
1. .
.
【解析 】 点M (x ,y )到直线x =4的距离是到点N (1,0)的距离的2倍,则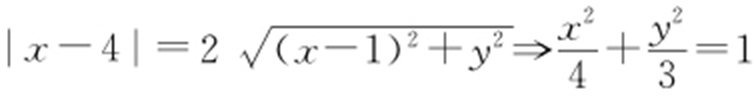 .所以动点M 的轨迹为椭圆,方程为
.所以动点M 的轨迹为椭圆,方程为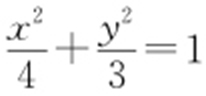 .
.
2.y 2 =8x .
【解析 】 设动圆圆心C 的坐标为(x ,y ),则(4-x )2 +(0-y )2 =42 +x 2 ,整理得y 2 =8x .所以,所求动圆圆心的轨迹C 的方程为y 2 =8x .
方法3 相关点法
y 2 =8-4x .
【解析 】 设动点P 的坐标为(x ,y ),点A 的坐标为(xA ,yA ),则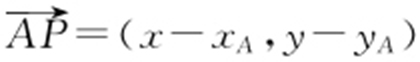 ,因为F 的坐标为(1,0),所以
,因为F 的坐标为(1,0),所以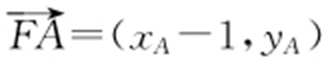 ,由
,由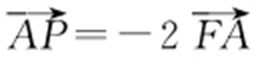 ,得(x -xA ,y -yA )=-2(xA -1,yA ).解得xA =2-x ,yA =-y .代入y 2 =4x ,得到动点P 的轨迹方程为y 2 =8-4x .
,得(x -xA ,y -yA )=-2(xA -1,yA ).解得xA =2-x ,yA =-y .代入y 2 =4x ,得到动点P 的轨迹方程为y 2 =8-4x .
方法4 消参法
(x +2)2 -y 2 =4(y ≠0).
【解析 】 当直线l 的斜率存在时,设l 的方程为y =k (x +2)(k ≠0),代入方程x 2 -y 2 =1,得(1-k 2 )x 2 -4k 2 x -4k 2 -1=0.
因为直线l 与双曲线有两个交点,所以1-k 2 ≠0,设A (x 1 ,y 1 ),B (x 2 ,y 2 ),则
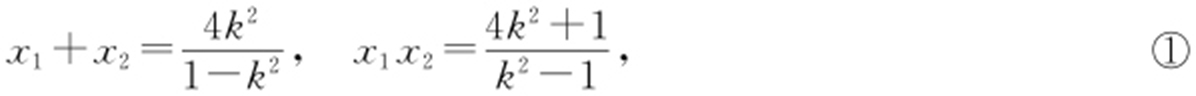
.
设P (x ,y ),由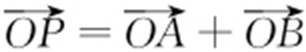 ,得
,得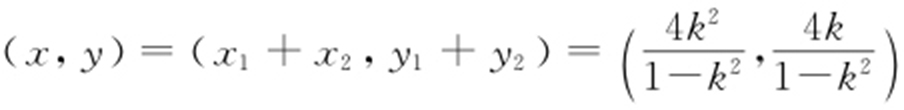 ,故
,故 所以
所以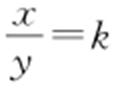 ,代入
,代入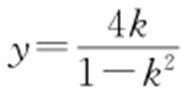 ,可得
,可得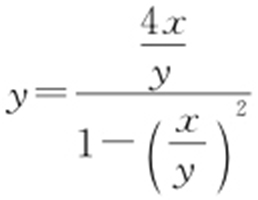 ,化简得x 2 -y 2 +4x =0,即
,化简得x 2 -y 2 +4x =0,即

当直线l 的斜率不存在时,易求得P (-4,0)满足方程②,故所求轨迹方程为(x +2)2 -y 2 =4(y ≠0),其轨迹为双曲线(也可考虑用点差法求解曲线方程).
考点2 点差法(中点弦公式)
.
考点3 弦长公式
【思路 】 (1)可设直线AB 的方程为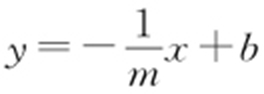 ,从而可知
,从而可知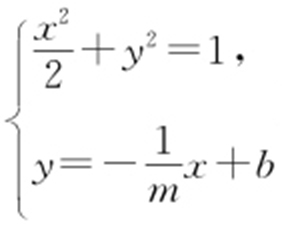 有两个不同的解,再由AB 中点也在直线上,即可得到关于m 的不等式,从而求解.
有两个不同的解,再由AB 中点也在直线上,即可得到关于m 的不等式,从而求解.
(2)令 ,可将△AOB 表示为t 的函数,从而将问题等价转化为在给定范围上求函数的最值,从而求解.
,可将△AOB 表示为t 的函数,从而将问题等价转化为在给定范围上求函数的最值,从而求解.
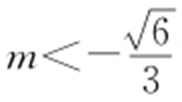 或
或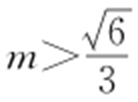 ,△AOB 面积最大值为
,△AOB 面积最大值为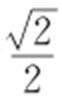 .
.
【解析 】 (1)由题意知m ≠0,可设直线AB 的方程为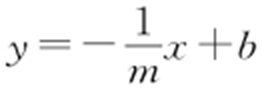 ,由
,由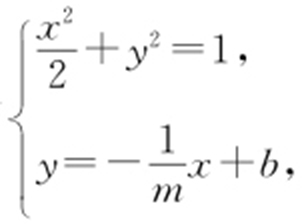 消去y ,得
消去y ,得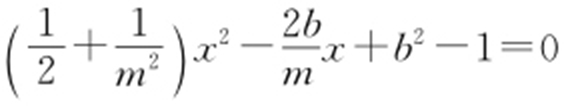 .因为直线
.因为直线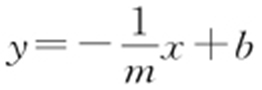 与椭圆
与椭圆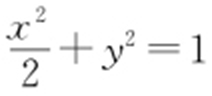 有两个不同的交点,所以
有两个不同的交点,所以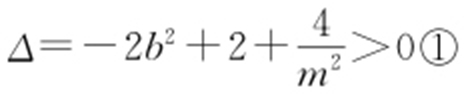 ,将AB 中点
,将AB 中点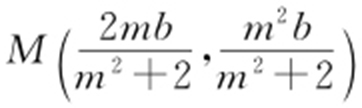 代入直线
代入直线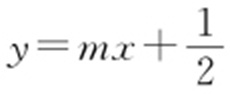 ,解得
,解得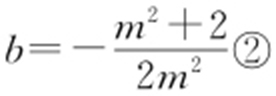 .由①,②得,
.由①,②得,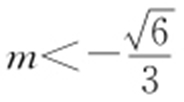 或
或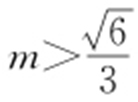 .
.
(2)令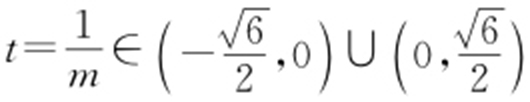 ,则
,则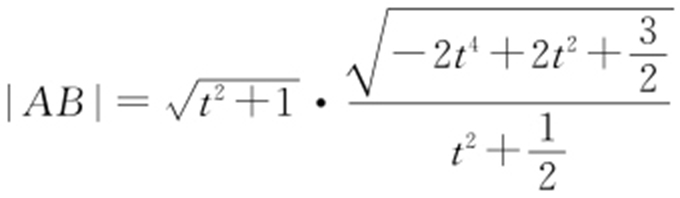 ,且O 到直线 AB 的距离为
,且O 到直线 AB 的距离为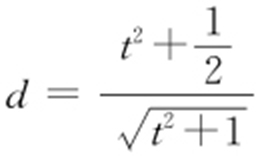 ,设△AOB 的面积为S (t ),则
,设△AOB 的面积为S (t ),则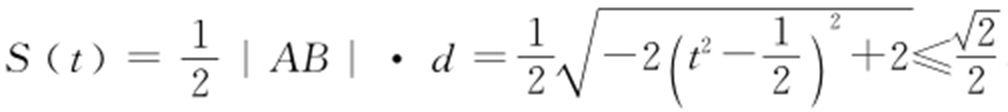 ,当且仅当
,当且仅当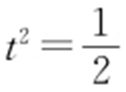 时,等号成立,故△AOB 面积的最大值为
时,等号成立,故△AOB 面积的最大值为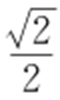 .
.
考点4 向量相关问题
1.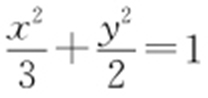 ,
,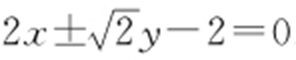 .
.
【解析 】 (1)由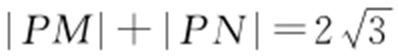 知道曲线C 是以M ,N 为焦点的椭圆,且
知道曲线C 是以M ,N 为焦点的椭圆,且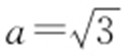 ,c =1,
,c =1,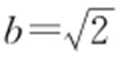 ,所以曲线C 的方程为
,所以曲线C 的方程为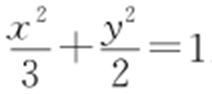 .
.
(2)设A (x 1 ,y 1 ),B (x 2 ,y 2 ),由题意知l 的斜率一定不为0,故不妨设l :x =my +1,代入椭圆方程整理,得(2m 2 +3)y 2 +4my -4=0,显然Δ >0,则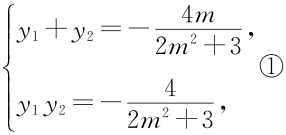
假设存在点Q ,使得四边形OAQB 为平行四边形,其充要条件为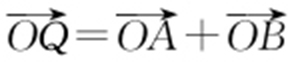 ,则点Q 的坐标为(x 1 +x 2 ,y 1 +y 2 ).点Q 在椭圆上,即
,则点Q 的坐标为(x 1 +x 2 ,y 1 +y 2 ).点Q 在椭圆上,即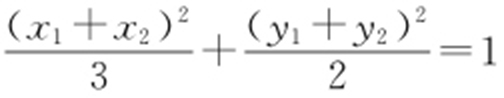 ,整理得
,整理得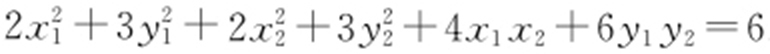 .又A ,B 在椭圆上,即
.又A ,B 在椭圆上,即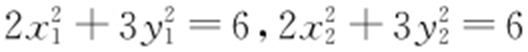 .故2x 1 x 2 +3y 1 y 2 =-3②,所以x 1 x 2 =(my 1 +1)(my 2 +1)=m 2 y 1 y 2 +m (y 1 +y 2 )+1,将①,②代入上式,解得
.故2x 1 x 2 +3y 1 y 2 =-3②,所以x 1 x 2 =(my 1 +1)(my 2 +1)=m 2 y 1 y 2 +m (y 1 +y 2 )+1,将①,②代入上式,解得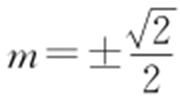 .即直线l 的方程是:
.即直线l 的方程是: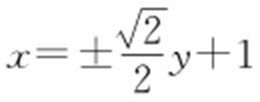 ,即
,即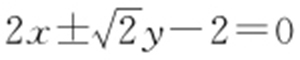 .
.
2.(1)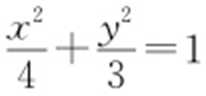 .(2)
.(2)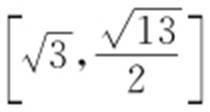 .
.
考点5 斜率问题
(1)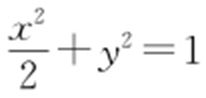 ,
, ;(2)存在,
;(2)存在,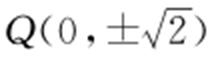 .
.
【解析 】 (1)由于椭圆C :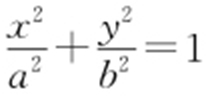 (a >b >0)过点P (0,1)且离心率为
(a >b >0)过点P (0,1)且离心率为 ,因此
,因此 ,
,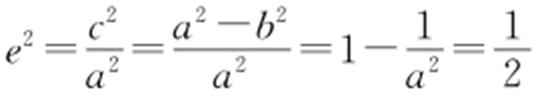 ,a 2 =2,椭圆C 的方程为
,a 2 =2,椭圆C 的方程为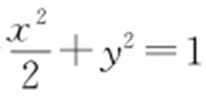 .
.
因为P (0,1),A (m ,n ),则直线PA 的方程为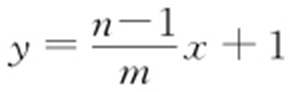 .令y =0,
.令y =0,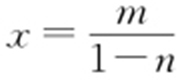 ,则
,则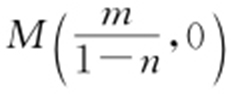 .
.
(2)因为P (0,1),B (m ,-n ),直线PB 的方程为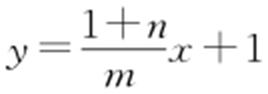 ,直线PB 与x 轴交于点N ,令y =0,
,直线PB 与x 轴交于点N ,令y =0,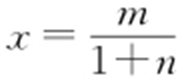 ,则
,则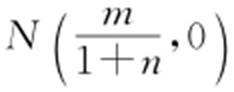 .设Q (0,y 0 ),
.设Q (0,y 0 ), ,
, 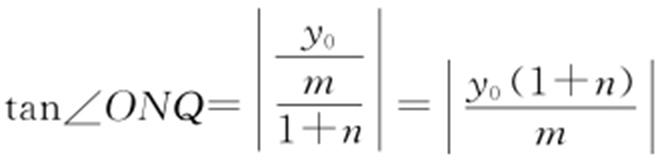 .
.
因为∠OQM =∠ONQ ,所以tan∠OQM =tan∠ONQ ,则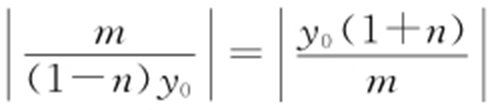 ,所以
,所以 (注:点A (m ,n )(m ≠0)在椭圆C 上,
(注:点A (m ,n )(m ≠0)在椭圆C 上,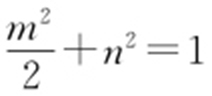 ),则
),则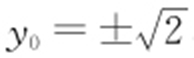 ,即存在点
,即存在点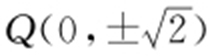 ,使得∠OQM =∠ONQ .
,使得∠OQM =∠ONQ .
考点6 切线问题
(1)x 2 =4y ;(2)x 0 x -2y -2y 0 =0;(3)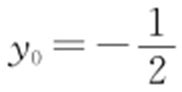 时,最小值为
时,最小值为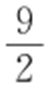 .
.
【解析 】 (1)依题意,设抛物线C 的方程为x 2 =4cy ,由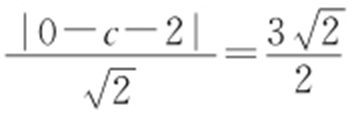 结合c >0,解得c =1.所以抛物线C 的方程为x 2 =4y .
结合c >0,解得c =1.所以抛物线C 的方程为x 2 =4y .
(2)抛物线C 的方程为x 2 =4y ,即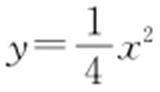 ,求导得
,求导得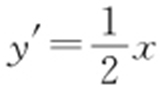 .
.
设A (x 1 ,y 1 ),B (x 2 ,y 2 )(其中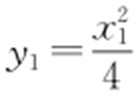 ,
,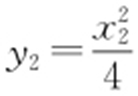 ),则切线PA ,PB 的斜率分别为
),则切线PA ,PB 的斜率分别为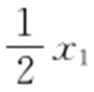 ,
,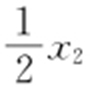 ,所以切线PA 的方程为
,所以切线PA 的方程为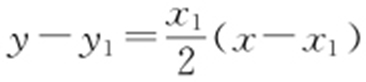 ,即
,即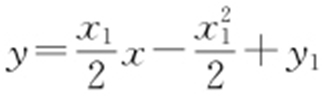 ,即x 1 x -2y -2y 1 =0.同理可得切线PB 的方程为x 2 x -2y -2y 2 =0.
,即x 1 x -2y -2y 1 =0.同理可得切线PB 的方程为x 2 x -2y -2y 2 =0.
因为切线PA ,PB 均过点P (x 0 ,y 0 ),所以x 1 x 0 -2y 0 -2y 1 =0,x 2 x 0 -2y 0 -2y 2 =0,所以(x 1 ,y 1 ),(x 2 ,y 2 )为方程x 0 x -2y 0 -2y =0的两组解.所以直线AB 的方程为x 0 x -2y -2y 0 =0.
(3)由抛物线定义可知|AF |=y 1 +1,|BF |=y 2 +1,所以|AF |·|BF |=(y 1 +1)·(y 2 +1)=y 1 y 2 +(y 1 +y 2 )+1.
联立方程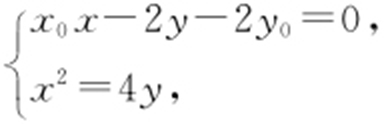 消去x 整理得
消去x 整理得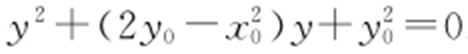 .由一元二次方程根与系数的关系可得
.由一元二次方程根与系数的关系可得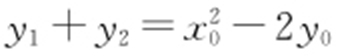 ,
, ,所以
,所以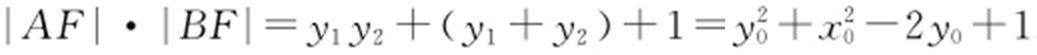 .
.
又点P (x 0 ,y 0 )在直线l 上,所以x 0 =y 0 +2,所以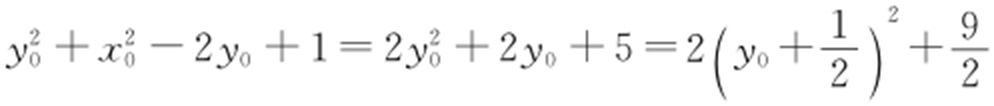 ,所以当
,所以当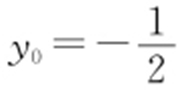 时,|AF |·|BF |取得最小值,且最小值为
时,|AF |·|BF |取得最小值,且最小值为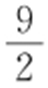 .
.
考点7 定点问题
y 2 =8x (x ≠0).
【解析 】 (1)设动圆圆心C 的坐标为(x ,y ),则(4-x )2 +(0-y )2 =42 +x 2 ,整理得y 2 =8x .所以,所求动圆圆心的轨迹C 的方程为y 2 =8x .
(2)证明:设直线l 的方程为y =kx +b ,联立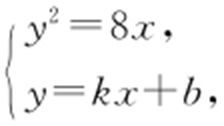 得k 2 x 2 +2kbx +b 2 =8x ⇒k 2 x 2 -(8-2kb )x +b 2 =0(其中Δ >0).设P (x 1 ,kx 1 +b ),Q (x 2 ,kx 2 +b ),若x 轴是∠PBQ 的 角平分线,则
得k 2 x 2 +2kbx +b 2 =8x ⇒k 2 x 2 -(8-2kb )x +b 2 =0(其中Δ >0).设P (x 1 ,kx 1 +b ),Q (x 2 ,kx 2 +b ),若x 轴是∠PBQ 的 角平分线,则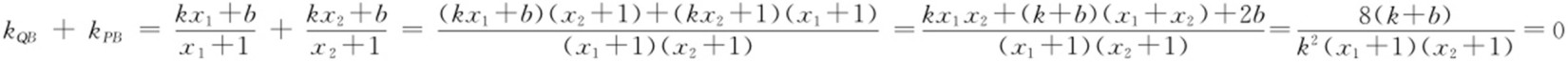 ,即k =-b ,故直线l 的方程为y =k (x -1),直线过定点(1,0).
,即k =-b ,故直线l 的方程为y =k (x -1),直线过定点(1,0).
第7章 参数方程与极坐标
一、参数方程
考点1 直线
(1)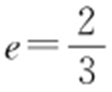 ;(2)
;(2)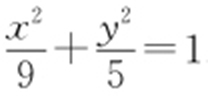 .
.
【解析 】 (1)设出直线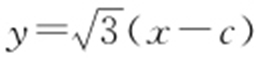 和椭圆方程联立,消去x 可以得到
和椭圆方程联立,消去x 可以得到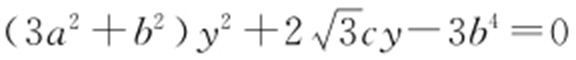 ,y 1 =-2y 2 .
,y 1 =-2y 2 .
可以得到a ,c 的关系,即 .
.
(2)略.
考点2 圆
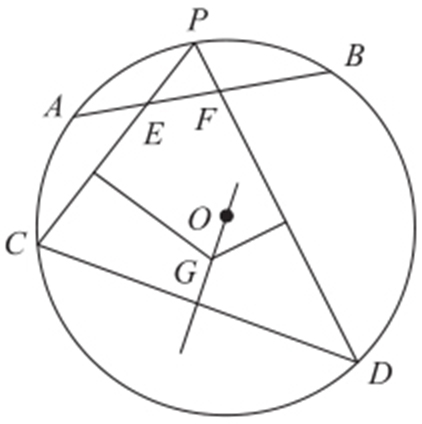
C.
【解析 】 画图,AD ,BD 都过圆心.
考点3 其他曲线
(1) (2)
(2)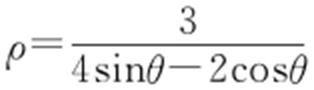 .
.
【解析 】 (2)联立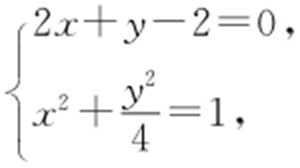 解得(1,0),(0,2),即y -1=0.5(x -0.5),再化为极坐标:
解得(1,0),(0,2),即y -1=0.5(x -0.5),再化为极坐标: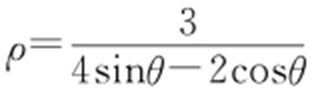 .
.
考点4 参数方程的应用最值问题
最大值为 ;最小值为
;最小值为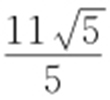 .
.
【解析 】 P (2cosθ ,3sinθ ),求到l 的距离d ,PA =d ,化简得最大值.
二、极坐标
考点1 直线
.
考点2 圆
1.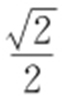 . 2.B.
. 2.B.
三、综合
(1)(0,0)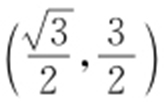 ;(2)最大值为4.
;(2)最大值为4.
【解析 】 (1)曲线C 2 的直角坐标方程为x 2 +y 2 -2y =0,曲线C 3 的直角坐标方程为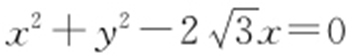 ,联立
,联立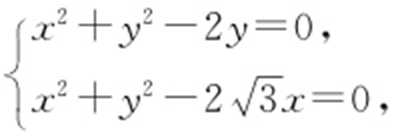 解得
解得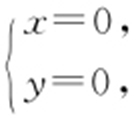 或
或 所以C 2 与C 1 交点的直角坐标为(0,0)和
所以C 2 与C 1 交点的直角坐标为(0,0)和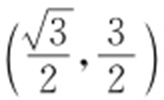 .
.
(2)曲线C 1 的极坐标方程为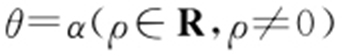 ,其中0≤α <π,因此得到A 的极坐标为(2sinα ,α ),B 的极坐标为
,其中0≤α <π,因此得到A 的极坐标为(2sinα ,α ),B 的极坐标为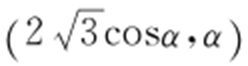 .所以
.所以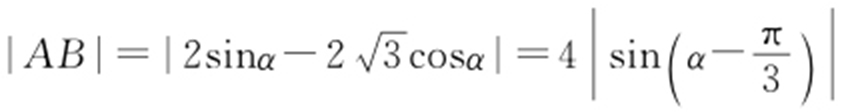 ,当
,当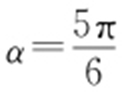 时,|AB |取得最大值,最大值为4.
时,|AB |取得最大值,最大值为4.
2.【解析 】 (1)C 1 的普通方程为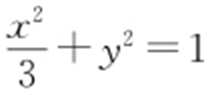 ,C 2 的直角坐标方程为x +y -4=0.
,C 2 的直角坐标方程为x +y -4=0.
(2)由题意,可设点P 的直角坐标为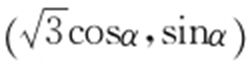 ,因为C 2 是直线,所以|PQ |得最小值,即为P 到C 2 的距离d (α )的最小值
,因为C 2 是直线,所以|PQ |得最小值,即为P 到C 2 的距离d (α )的最小值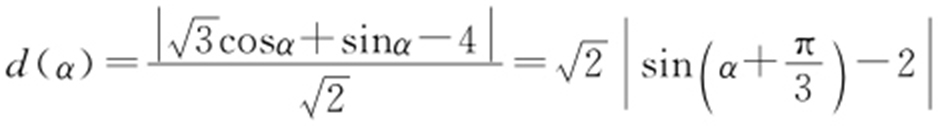 .当且仅当
.当且仅当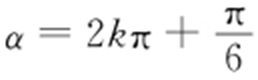 (k ∈Z )时,d (α )取得最小值,最小值为
(k ∈Z )时,d (α )取得最小值,最小值为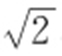 ,此时P 的直角坐标为
,此时P 的直角坐标为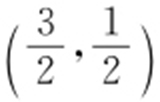 .
.
3.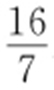 .
.
【解析 】 直线l 方程化为普通方程为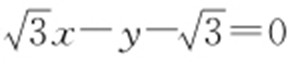 ,椭圆C 方程化为普通方程为
,椭圆C 方程化为普通方程为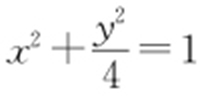 ,联立得
,联立得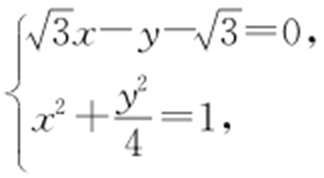 解得
解得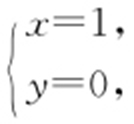 或
或 因此
因此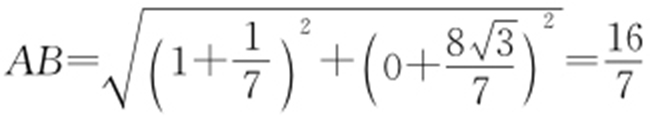 .
.
第8章 解析几何2015年真题必刷
直线与圆
1.D.
【解析 】 因为直线3x +4y =b 与圆心为(1,1)、半径为1的圆相切,所以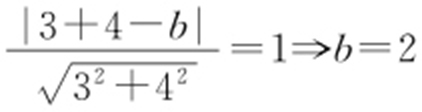 或b =12.
或b =12.
【考点 】 直线与圆的位置关系;点到直线的距离公式.
2.D.
【解析 】 由题意可得,圆的半径为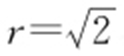 ,则圆的标准方程为(x -1)2 +(y -1)2 =2.
,则圆的标准方程为(x -1)2 +(y -1)2 =2.
【考点 】 圆的标准方程.
3.D.
【解析 】 设所求切线方程为2x +y +c =0,依题有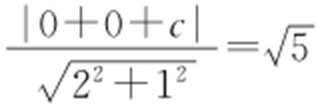 ,解得c =±5,所以所求切线的直线方程为2x +y +5=0或2x +y -5=0,故选:D.
,解得c =±5,所以所求切线的直线方程为2x +y +5=0或2x +y -5=0,故选:D.
【考点 】 本题考查直线与圆的位置关系.
4.【解析 】 (1)因为圆C 1 :x 2 +y 2 -6x +5=0,整理,得其标准方程为(x -3)2 +y 2 =4,所以圆C 1 的圆心坐标为(3,0).
(2)设当直线l 的方程为y =kx ,A (x 1 ,y 1 ),B (x 2 ,y 2 ),联立方程组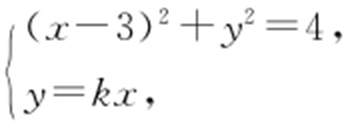 消去y ,可得(1+k 2 )x 2 -6x +5=0,由Δ =36-4(1+k 2 )×5>0,可得
消去y ,可得(1+k 2 )x 2 -6x +5=0,由Δ =36-4(1+k 2 )×5>0,可得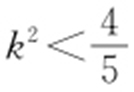 .
.
由韦达定理,可得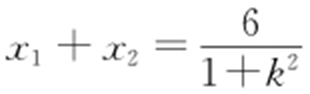 ,所以线段AB 的中点M 的轨迹C 的参数方程为
,所以线段AB 的中点M 的轨迹C 的参数方程为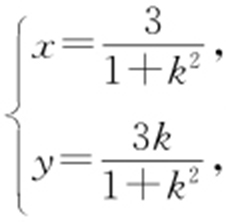 其中
其中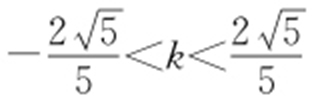 ,所以线段AB 的中点M 的轨迹C 的方程为
,所以线段AB 的中点M 的轨迹C 的方程为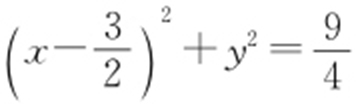 ,其中
,其中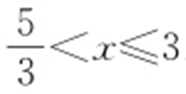 .
.
(3)结论:当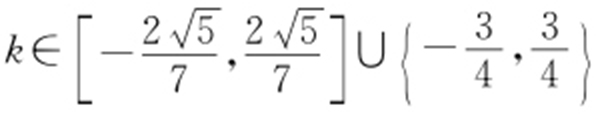 时,直线l :y =k (x -4)与曲线C 只有一个交点.
时,直线l :y =k (x -4)与曲线C 只有一个交点.
理由如下:联立方程组 消去y ,可得(1+k 2 )x 2 -(3+8k )x +16k 2 =0,令Δ =(3+8k )2 -4(1+k 2 )·16k 2 =0,解得
消去y ,可得(1+k 2 )x 2 -(3+8k )x +16k 2 =0,令Δ =(3+8k )2 -4(1+k 2 )·16k 2 =0,解得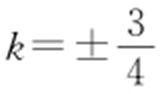 .
.
又因为轨迹C 的端点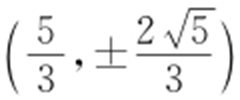 与点(4,0)决定的直线斜率为
与点(4,0)决定的直线斜率为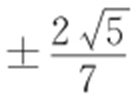 ,所以当直线l : y =k (x -4)与曲线C 只有一个交点时,k 的取值范围为
,所以当直线l : y =k (x -4)与曲线C 只有一个交点时,k 的取值范围为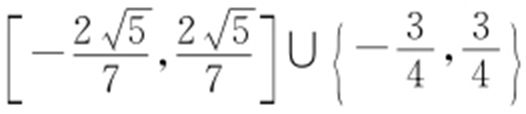 .
.
【考点 】 轨迹方程;直线与圆的位置关系.
5.(1)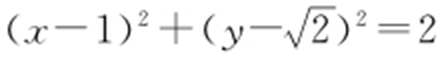 ;(2)
;(2)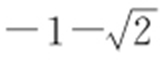 .
.
【考点 】 圆的几何知识.
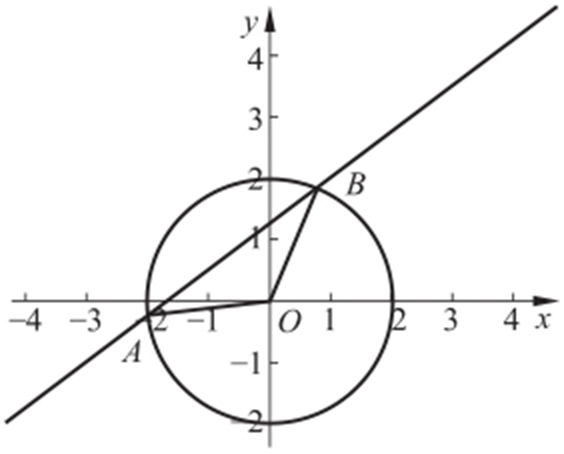
6.2.
【解析 】 如图,直线3x -4y +5=0与圆x 2 +y 2 =r 2 (r >0)交于A ,B 两点,O 为坐标原点,且∠AOB =120°,则圆心(0,0)到直线3x -4y +5=0的距离为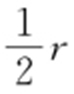 ,
,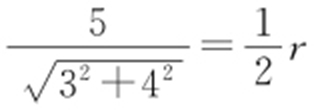 ,则r =2,故答案为2.
,则r =2,故答案为2.
【考点 】 直线与圆的位置关系.
7.D.
【解析 】 点A (-2,-3)关于y 轴的对称点为A′ (2,-3),故可设反射光线所在直线的方程为y +3=k (x -2),化为kx -y -2k -3=0.
因为反射光线与圆(x +3)2 +(y -2)2 =1相切,所以圆心(-3,2)到直线的距离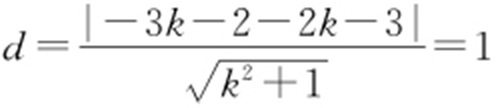 ,化为24k 2 +50k +24=0,所以
,化为24k 2 +50k +24=0,所以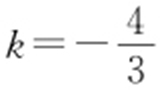 或
或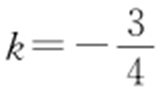 .故选:D.
.故选:D.
【考点 】 圆的切线方程;直线的斜率.
8.A.
【解析 】 由相交弦定理可知,AM ·MB =CM ·MD ,CN ·NE =AN ·NB ,又因为M ,N 是弦AB 的三等分点,所以AM ·MB =AN ·NB ,所以CN ·NE =CM ·MD ,所以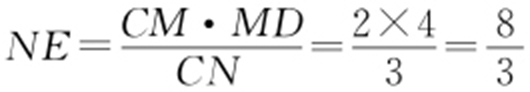 .故选:A.
.故选:A.
【考点 】 相交弦定理.
9.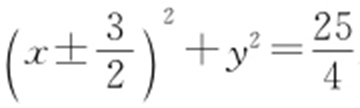 .
.
【解析 】 设圆心为(a ,0),a >0,则半径为4-|a |,则(4-|a |)2 =|a |2 +22 ,解得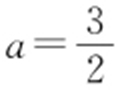 ,故圆的方程为
,故圆的方程为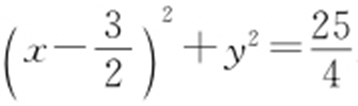 .
.
【考点 】 椭圆的几何性质;圆的标准方程.
10.(1)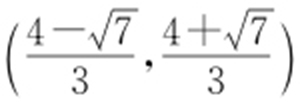 ;(2)|MN |=2.
;(2)|MN |=2.
【解析 】 (1)由题设,可知直线l 的方程为y =kx +1.因为l 与C 交于两点,所以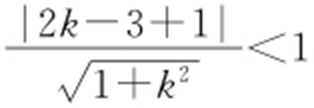 .解得
.解得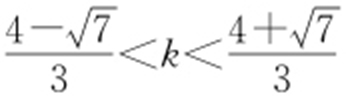 .所以k 的取值范围为
.所以k 的取值范围为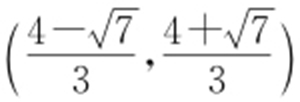 .
.
(2)设M (x 1 ,y 1 ),N (x 2 ,y 2 ).将y =kx +1代入方程(x -2)2 +(y -3)2 =1,整理得(1+k 2 )x 2 -4(1+k )x +7=0.所以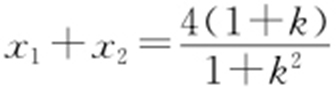 ,
,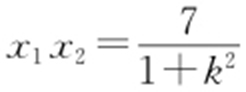 .
.
.
由题设可得=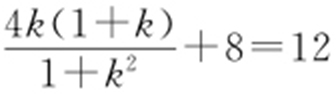 ,解得k =1,所以l 的方程是y =x +1.
,解得k =1,所以l 的方程是y =x +1.
故圆心C 在l 上,所以|MN |=2.
11.C.
【解析 】 由已知得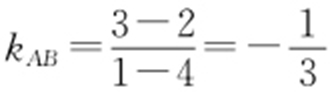 ,
,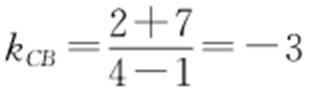 ,所以kAB kCB =-1,所以AB ⊥CB ,即△ABC 为直角三角形,其外接圆圆心为(1,-2),半径为5,所以外接圆方程为(x -1)2 +(y +2)2 =25,令x =0,得
,所以kAB kCB =-1,所以AB ⊥CB ,即△ABC 为直角三角形,其外接圆圆心为(1,-2),半径为5,所以外接圆方程为(x -1)2 +(y +2)2 =25,令x =0,得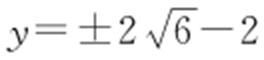 ,所以
,所以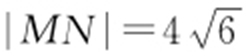 .故选:C.
.故选:C.
【考点 】 圆的方程.
12.B.
【解析 】 根据题意,△ABC 是等边三角形,设外接圆的圆心为D ,则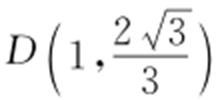 .所以
.所以 .故选:B.
.故选:B.
【考点 】 三角形的外接圆.
13.C.
【解析 】 圆C 标准方程为(x -2)2 +(y -1)2 =4,圆心为C (2,1),半径为r =2,因此2+a ×1-1=0,a =-1,即A (-4,-1),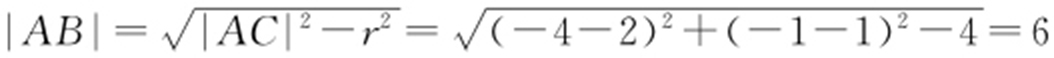 .故选:C.
.故选:C.
【考点 】 直线与圆的位置关系.
圆锥曲线
14.C.
【解析 】 由题意得:m 2 =25-42 =9,因为m >0,所以m =3.故选:C.
【考点 】 椭圆的几何性质.
15.C.
【考点 】 椭圆的概念.
16. .
.
【解析 】 设F (c ,0)关于直线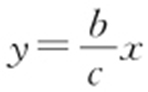 的对称点为Q (m ,n ),则有
的对称点为Q (m ,n ),则有 解得
解得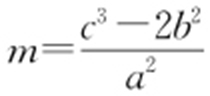 ,
,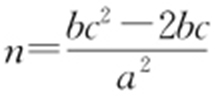 ,所以
,所以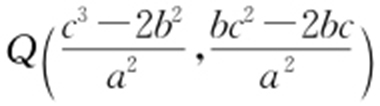 在椭圆上,即有
在椭圆上,即有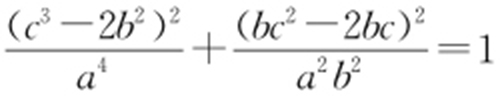 ,解得a 2 =2c 2 ,所以离心率
,解得a 2 =2c 2 ,所以离心率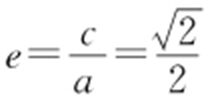 .
.
【考点 】 点关于直线对称;椭圆的离心率.
17.(1)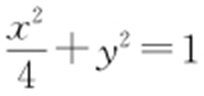 ;(2)
;(2)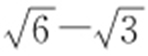 .
.
【解析 】 (1)由椭圆的定义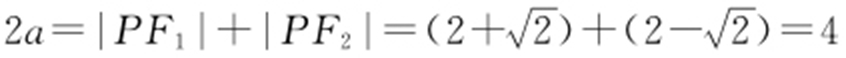 ,故a =2.
,故a =2.
设椭圆的半焦距为c ,由已知PF 1 ⊥PF 2 ,因此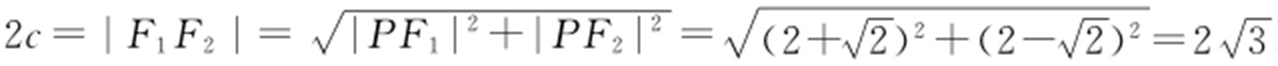 ,即
,即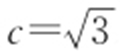 .从而
.从而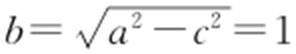 ,故所求椭圆的标准方程为
,故所求椭圆的标准方程为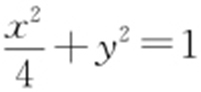 .
.
(2)解法1:设点P (x 0 ,y 0 )在椭圆上,且PF 1 ⊥PF 2 ,则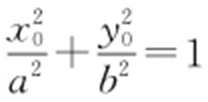 ,
,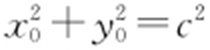 .求得
.求得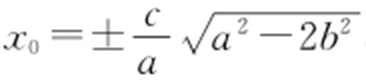 ,
, .
.
由|PF 1 |=|PQ |>|PF 2 |,得x 0 >0,从而
.
由椭圆的定义,|PF 1 |+|PF 2 |=2a ,|QF 1 |+|QF 2 |=2a ,从而由|PF 1 |=|PQ |=|PF 2 |+|QF 2 |,有|QF 1 |=4a -2|PF 1 |.
又由PF 1 ⊥PF 2 ,|PF 1 |=|PQ |,知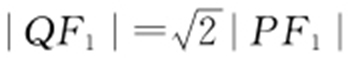 ,因此
,因此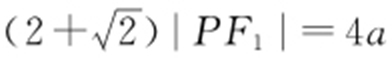 ,于是
,于是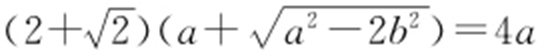 .解得
.解得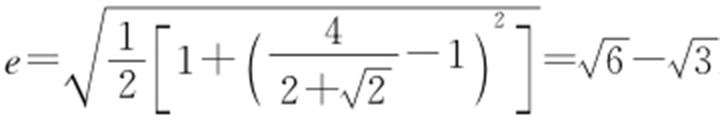 .
.
解法2:由椭圆的定义,|PF 1 |+|PF 2 |=2a ,|QF 1 |+|QF 2 |=2a ,从而由|PF 1 |=|PQ |=|PF 2 |+|QF 2 |,有|QF 1 |=4a -2|PF 1 |.
又由PF 1 ⊥PF 2 ,|PF 1 |=|PQ |,知 ,因此
,因此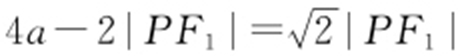 ,即
,即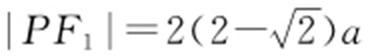 ,从而
,从而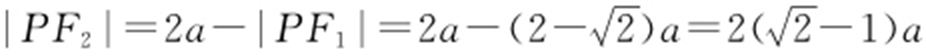 .
.
由PF 1 ⊥PF 2 ,知|PF 1 |2 +|PF 2 |2 =|PF 2 |2 =(2c )2 =4c 2 ,因此
.
18.B.
【解析 】 由双曲线定义得||PF 1 |-|PF 2 ||=2a =6,即|3-|PF 2 ||=6,解得|PF 2 |=9.故选:B.
【考点 】 双曲线的标准方程和定义.
19.C.
【解析 】 由题意,选项A,B的焦点在x 轴,故排除A,B,C项的渐近线方程为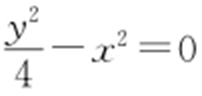 ,即y =±2x .故选:C.
,即y =±2x .故选:C.
【考点 】 双曲线的渐近线.
20.A.
【解析 】 由双曲线的渐进线的公式可行选项A的渐进线方程为y =±2x .故选:A.
【考点 】 渐近线方程.
21.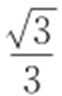 .
.
【解析 】 双曲线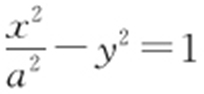 (a >0)的渐近线方程为
(a >0)的渐近线方程为 ,
,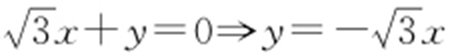 ,因为a >0,所以
,因为a >0,所以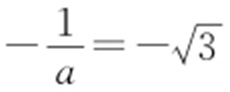 ,即
,即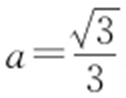 .
.
【考点 】 双曲线的几何性质.
22.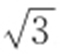 .
.
【解析 】 由题意知c =2,a =1,b 2 =c 2 -a 2 =3,所以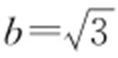 .
.
【考点 】 双曲线的焦点.
23.B.
【解析 】 因为所求双曲线的右焦点为F 2 (5,0)且离心率为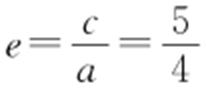 ,所以c =5,a =4,b 2 =c 2 -a 2 =9所以所求双曲线方程为
,所以c =5,a =4,b 2 =c 2 -a 2 =9所以所求双曲线方程为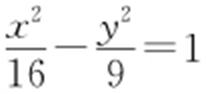 ,故选:B.
,故选:B.
【考点 】 双曲线的标准方程及其几何性质.
24.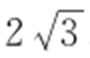 ;
;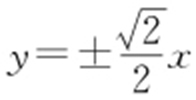 .
.
【解析 】 由题意得: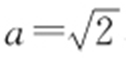 ,b =1,
,b =1,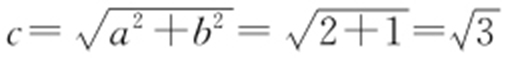 ,所以焦距为
,所以焦距为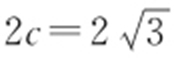 ,渐近线方程为
,渐近线方程为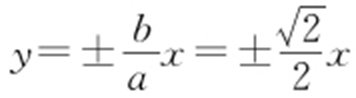 .
.
【考点 】 双曲线的标准方程及其几何性质.
25.D.
【解析 】 由题意得a =1,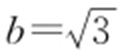 ,故c =2,则渐近线为
,故c =2,则渐近线为 ,将x =2代入渐近线,得
,将x =2代入渐近线,得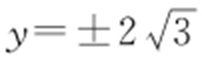 ,所以
,所以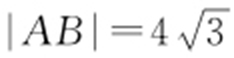 .
.
26.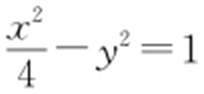 .
.
【解析 】 根据双曲线渐近线方程为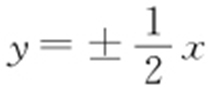 ,可设双曲线的方程为
,可设双曲线的方程为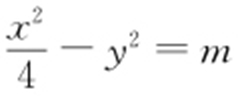 ,把
,把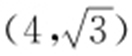 代入
代入 ,得m =1,所以双曲线的方程为
,得m =1,所以双曲线的方程为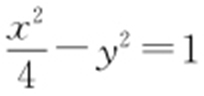 .
.
【考点 】 双曲线几何性质.
27.D.
【解析 】 双曲线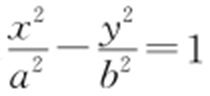 (a >0,b >0)的渐近线方程为
(a >0,b >0)的渐近线方程为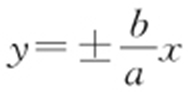 ,由点
,由点 在渐近线上,所以
在渐近线上,所以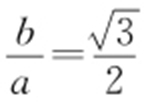 ,双曲线的一个焦点在抛物线
,双曲线的一个焦点在抛物线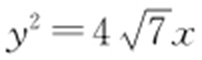 准线方程
准线方程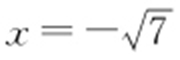 上,所以
上,所以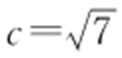 ,由此可解得a =2,
,由此可解得a =2, ,所以双曲线方程为
,所以双曲线方程为 .故选:D.
.故选:D.
【考点 】 双曲线的标准方程及几何性质;抛物线的标准方程及几何性质.
28.D.
【解析 】 由题意可得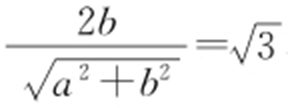 ,则c =2,a =1,
,则c =2,a =1,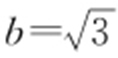 .
.
【考点 】 圆与双曲线的几何性质.
29.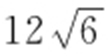 .
.
【解析 】 设双曲线的左焦点为F 1 ,由双曲线定义知,|PF |=2a +|PF 1 |,所以△APF 的周长为|PA |+|PF |+|AF |=|PA |+2a +|PF 1 |+|AF |=|PA |+|PF 1 |+|AF |+2a ,由 于2a +|AF |是定值,要使△APF 的周长最小,则|PA |+|PF 1 |最小,即P ,A ,F 1 共线.
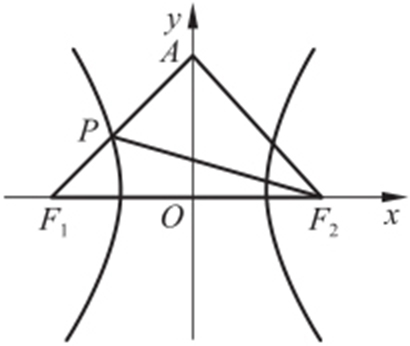
因为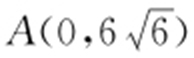 ,F 1 (-3,0),所以直线AF 1 的方程为
,F 1 (-3,0),所以直线AF 1 的方程为 ,即
,即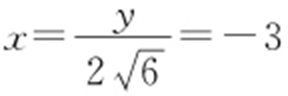 .代入
.代入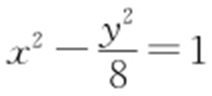 ,整理得
,整理得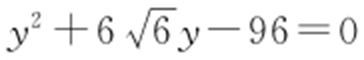 ,解得
,解得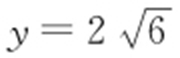 或
或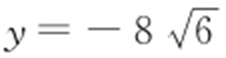 (舍),所以P 点的纵坐标为
(舍),所以P 点的纵坐标为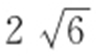 ,所以
,所以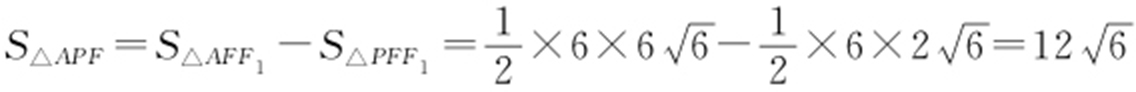 .
.
【考点 】 双曲线的定义;直线与双曲线的位置关系;最值问题.
30.A.
【解析 】 由题意知A (a ,0),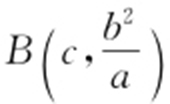 ,
,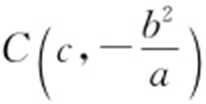 ,由双曲线的对称性,知D 在x 轴上,设D (x ,0),由BD ⊥AC ,得
,由双曲线的对称性,知D 在x 轴上,设D (x ,0),由BD ⊥AC ,得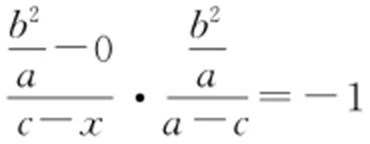 ,解得
,解得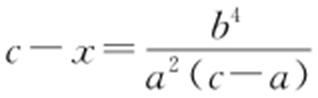 ,所以
,所以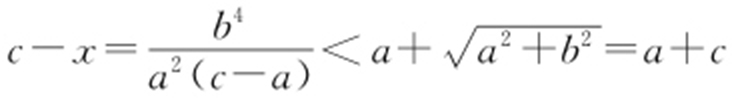 ,所以
,所以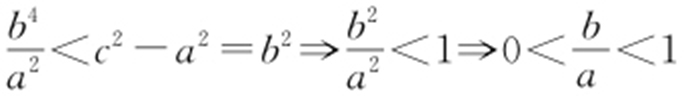 ,因此渐近线的斜率取值范围是(-1,0)∪(0,1).故选:A.
,因此渐近线的斜率取值范围是(-1,0)∪(0,1).故选:A.
【考点 】 双曲线的几何性质.
31.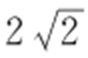 .
.
【解析 】 准线y 2 =2px (p >0)的准线方程为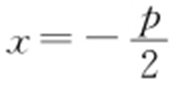 ,双曲线x 2 -y 2 =1的一个焦点
,双曲线x 2 -y 2 =1的一个焦点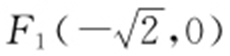 ,因为抛物线y 2 =2px 的准线经过双曲线焦点,所以
,因为抛物线y 2 =2px 的准线经过双曲线焦点,所以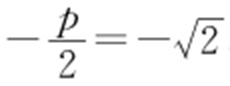 ,解得
,解得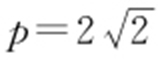 .
.
【考点 】 抛物线的几何性质;双曲线的几何性质.
32.B.
【解析 】 由抛物线y 2 =2px (p >0)得准线 ,因为准线经过点(-1,1),所以p =2,所以抛物线焦点坐标为(1,0),故选:B.
,因为准线经过点(-1,1),所以p =2,所以抛物线焦点坐标为(1,0),故选:B.
【考点 】 抛物线方程.
33.D.
【解析 】 不妨设直线l :x =ty +m ,代入抛物线方程有y 2 -4ty -4m =0,则Δ =16t 2 +16m >0.又中点M (2t 2 +m ,2t ),则kMC ·kl =-1,即m =3-2t 2 (当t ≠0时),代入Δ =16t 2 +16m ,可得3-t 2 >0,即0<t 2 <3.
又由圆心到直线的距离等于半径,可得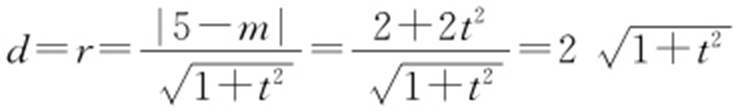 .
.
由0<t 2 <3,可得r ∈(2,4).故选:D.
【考点 】 直线与抛物线的位置关系;直线与圆的位置关系.
34.B.
【解析 】 因为抛物线C :y 2 =8x 的焦点为(2,0),准线方程为x =-2,所以椭圆E 的右焦点为(2,0),所以椭圆E 的焦点在x 轴上,设方程为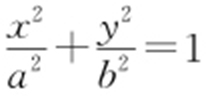 (a >b >0),c =2.
(a >b >0),c =2.
因为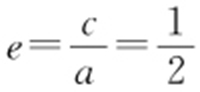 ,所以a =4,所以b 2 =a 2 -c 2 =12,故椭圆E 的方程为
,所以a =4,所以b 2 =a 2 -c 2 =12,故椭圆E 的方程为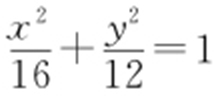 ,将x =-2代入椭圆E 的方程,解得A (-2,3),B (-2,-3),所以|AB |=6.故选:B.
,将x =-2代入椭圆E 的方程,解得A (-2,3),B (-2,-3),所以|AB |=6.故选:B.
【考点 】 抛物线的几何性质;椭圆的标准方程与几何性质.
35.A.
【解析 】 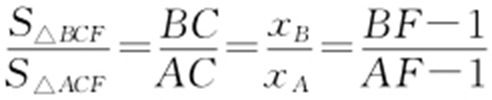 .故选:A.
.故选:A.
【考点 】 抛物线的标准方程及其几何性质.
36.A.
【解析 】 设左焦点为F ,连接AF 1 ,BF 1 ,则四边形BF 1 AF 是平行四边形,故|AF 1 |=|BF |,所以|AF |+|AF 1 |=4=2a ,所以a =2,设M (0,b ),则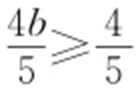 ,故b ≥1,从而a 2 -c 2 ≥1,0<c 2 ≤3,
,故b ≥1,从而a 2 -c 2 ≥1,0<c 2 ≤3,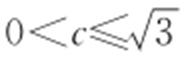 ,所以椭圆E 的离心率的取值范围是
,所以椭圆E 的离心率的取值范围是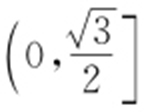 .故选:A.
.故选:A.
【考点 】 椭圆的定义和几何性质;点到直线的距离公式.
37.D.
【解析 】 不妨设双曲线C 1 的焦点在x 轴上,即其方程为 ,则双曲线C 2 的方程为
,则双曲线C 2 的方程为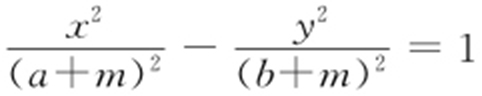 ,所以
,所以 ,
, .当a >b 时,
.当a >b 时,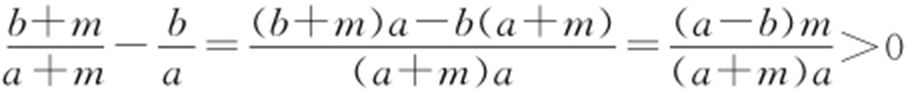 ,所以
,所以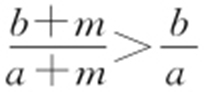 ,所以
,所以 ,所以e 2 >e 1 ;当a <b 时,
,所以e 2 >e 1 ;当a <b 时,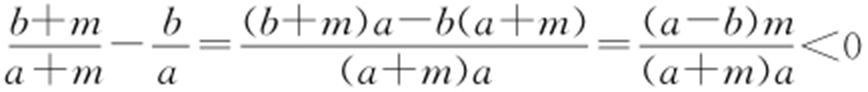 ,所以
,所以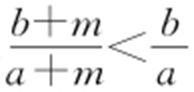 ,所以
,所以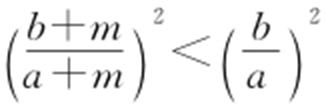 ,所以e 2 <e 1 ;故选:D.
,所以e 2 <e 1 ;故选:D.
【考点 】 双曲线的定义;双曲线的几何性质.
38.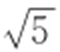 .
.
【解析 】 根据对称性,不妨设F (c ,0),短轴端点为(0,b ),从而可知点(-c ,2b )在双曲线上,所以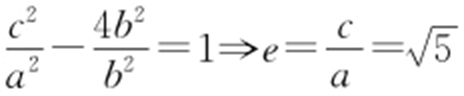 .
.
【考点 】 双曲线的标准方程及其几何性质.
39.D.
【解析 】 因为双曲线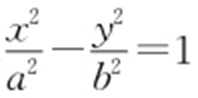 的一条渐近线经过点(3,-4),所以3b =4a ,则9(c 2 -a 2 )=16a 2 ,即
的一条渐近线经过点(3,-4),所以3b =4a ,则9(c 2 -a 2 )=16a 2 ,即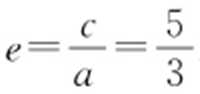 .故选:D.
.故选:D.
【考点 】 双曲线的几何性质.
40.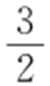 .
.
【解析 】 设OA 所在的直线方程为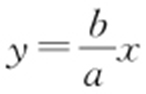 ,则OB 所在的直线方程为
,则OB 所在的直线方程为 ,解方程 组
,解方程 组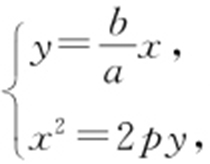 得
得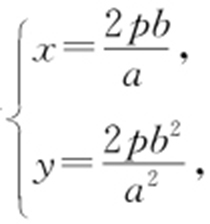 所以点A 的坐标为
所以点A 的坐标为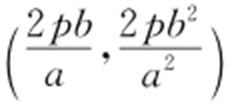 .
.
抛物线的焦点F 的坐标为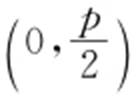 ,因为F 是△ABC 的垂心,所以kOB ·kAF =-1,所以,
,因为F 是△ABC 的垂心,所以kOB ·kAF =-1,所以, .
.
即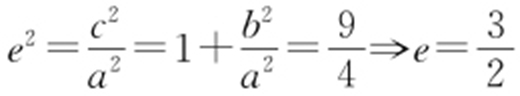 .
.
【考点 】 双曲线的标准方程与几何性质;抛物线的标准方程与几何性质.
41.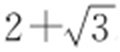 .
.
【解析 】 双曲线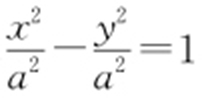 的右焦点为(c ,0).不妨设所作直线与双曲线的渐近线
的右焦点为(c ,0).不妨设所作直线与双曲线的渐近线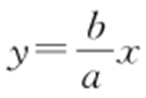 平行,其方程为
平行,其方程为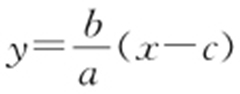 ,代入
,代入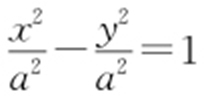 求得点P 的横坐标为
求得点P 的横坐标为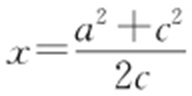 ,由
,由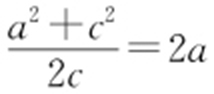 ,得
,得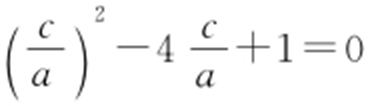 ,解之得
,解之得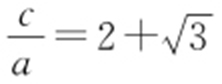 ,
,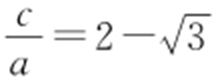 (舍去,因为离心率
(舍去,因为离心率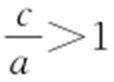 ),故双曲线的离心率为
),故双曲线的离心率为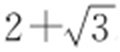 .
.
【考点 】 双曲线的几何性质;直线方程.
42.A.
【解析 】 由题意知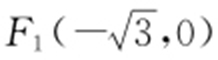 ,
,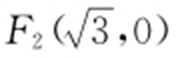 ,
,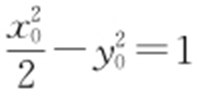 ,所以
,所以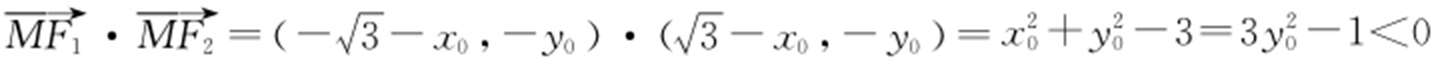 ,解得
,解得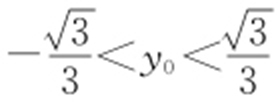 .故选:A.
.故选:A.
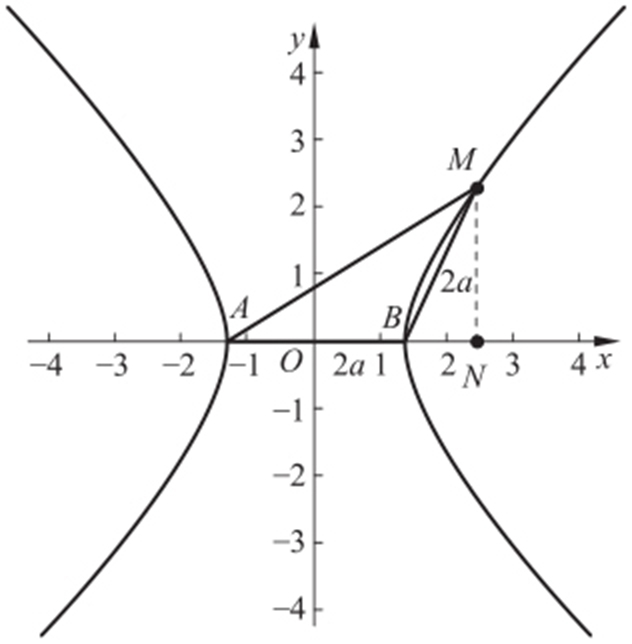
【考点 】 向量数量积;双曲线的标准方程.
43.D.
【解析 】 设双曲线方程为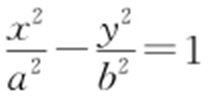 (a >0,b >0),如图所示,|AB |=|BM |,∠ABM =120°,过点M 作MN ⊥x 轴,垂足为N ,在Rt△BMN 中,|BN |=a ,
(a >0,b >0),如图所示,|AB |=|BM |,∠ABM =120°,过点M 作MN ⊥x 轴,垂足为N ,在Rt△BMN 中,|BN |=a ,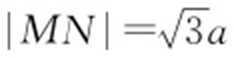 ,故点M 的坐标为
,故点M 的坐标为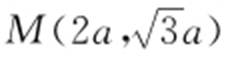 ,代入双曲线方程得a 2 =b 2 =a 2 -c 2 ,即c 2 =2a 2 ,所以
,代入双曲线方程得a 2 =b 2 =a 2 -c 2 ,即c 2 =2a 2 ,所以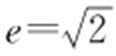 .故选:D.
.故选:D.
【考点 】 双曲线的标准方程和几何性质.
44.(1)详见解析;(2)能,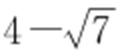 或
或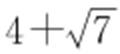 .
.
【解析 】 (1)设直线l :y =kx +b (k ≠0,b ≠0),A (x 1 ,y 1 ),B (x 2 ,y 2 ),M (xM ,yM ).将y =kx +b 代入9x 2 +y 2 =m 2 ,得(k 2 +9)x 2 +2kbx +b 2 -m 2 =0,故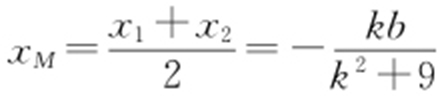 ,
, ,于是直线OM 的斜率
,于是直线OM 的斜率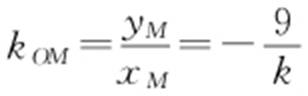 ,即kOM ·k =-9,所以直线OM 的斜率 与l 的斜率的乘积为定值.
,即kOM ·k =-9,所以直线OM 的斜率 与l 的斜率的乘积为定值.
(2)四边形OAPB 能为平行四边形.因为直线l 过点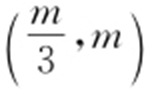 ,所以l 不过原点且与C 有两个交点的充要条件是k >0,k ≠3.由(1)得,OM 的方程为
,所以l 不过原点且与C 有两个交点的充要条件是k >0,k ≠3.由(1)得,OM 的方程为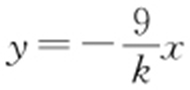 .设点P 的横坐标为xP ,由
.设点P 的横坐标为xP ,由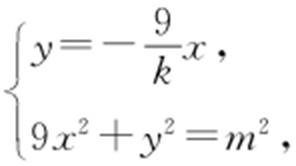 得
得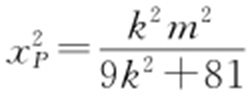 ,即
,即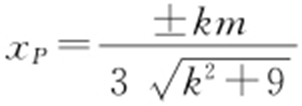 .将点
.将点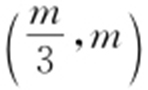 的坐标代入直线l 的方程得
的坐标代入直线l 的方程得 ,因此
,因此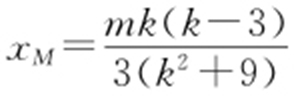 .四边形OAPB 为平行四边形当且仅当线段AB 与线段OP 互相平分,即xP =2xM .于是
.四边形OAPB 为平行四边形当且仅当线段AB 与线段OP 互相平分,即xP =2xM .于是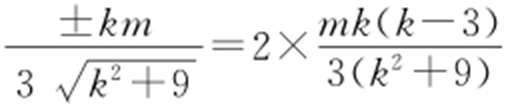 .解得
.解得 ,
,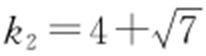 .因此ki >0,ki ≠3,i =1,2,所以当l 的斜率为
.因此ki >0,ki ≠3,i =1,2,所以当l 的斜率为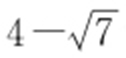 或
或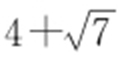 时,四边形OAPB 为平行四边形.
时,四边形OAPB 为平行四边形.
【考点 】 弦的中点问题;直线和椭圆的位置关系.
45.(1)A (2t ,t 2 ), ;(2)
;(2)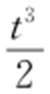 .
.
【解析 】 (1)由题意可知,直线PA 的斜率存在,故可设直线PA 的方程为y =k (x -t ).所以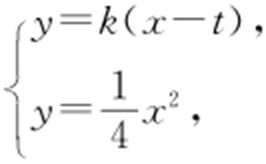 消去y ,整理得x 2 -4kx +4kt =0.
消去y ,整理得x 2 -4kx +4kt =0.
因为直线PA 与抛物线相切,所以Δ =16k 2 -16kt =0,解得k =t .所以x =2t ,即点A (2t ,t 2 ).设圆C 2 的圆心为D (0,1),点B 的坐标为(x 0 ,y 0 ),由题意知,点B ,O 关于直线PD 对称,故有 解得
解得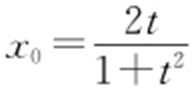 ,
,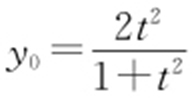 ,即点
,即点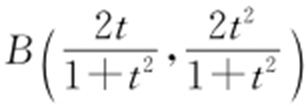 .
.
(2)由(1)知,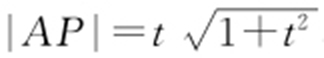 ,直线PA 的方程为tx -y -t 2 =0,所以点B 到直线PA 的距离为
,直线PA 的方程为tx -y -t 2 =0,所以点B 到直线PA 的距离为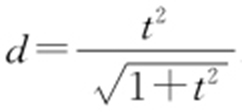 .所以△PAB 的面积为
.所以△PAB 的面积为 .
.
【考点 】 抛物线的几何性质;直线与圆的位置关系;直线与抛物线的位置关系.
46.(1)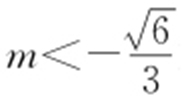 或
或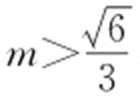 ;(2)
;(2)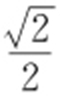 .
.
【解析 】 (1)由题意知,m ≠0,可设直线AB 的方程为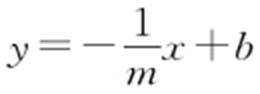 ,由
,由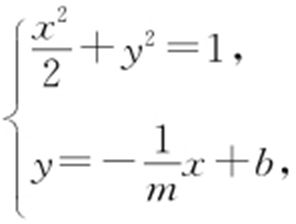 消去y ,得
消去y ,得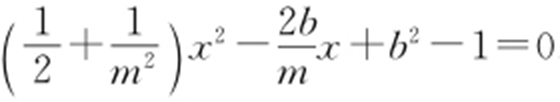 .因为直线
.因为直线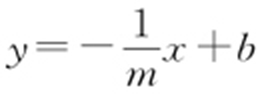 与椭圆
与椭圆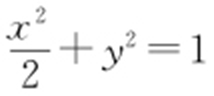 有两个不同的交点,所以
有两个不同的交点,所以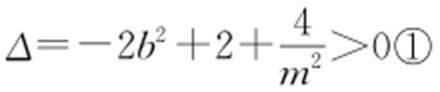 ,将AB 中点
,将AB 中点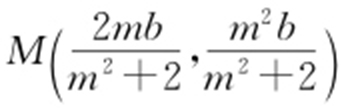 代入直线方程
代入直线方程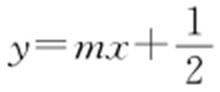 ,解得
,解得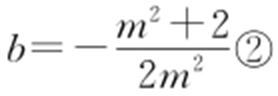 .由①、②得,
.由①、②得,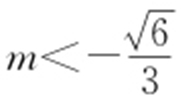 或
或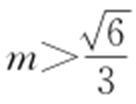 .
.
(2)令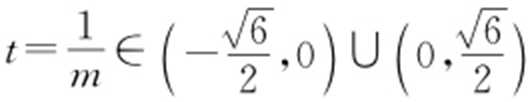 ,则
,则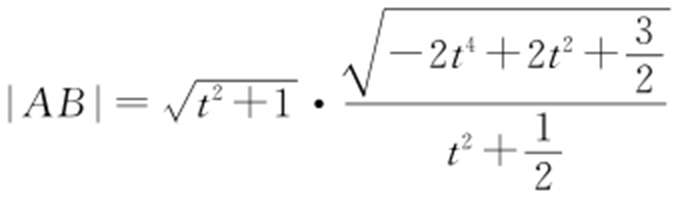 ,且O 到直线AB 的距离为
,且O 到直线AB 的距离为 ,设△AOB 的面积为S (t ),所以
,设△AOB 的面积为S (t ),所以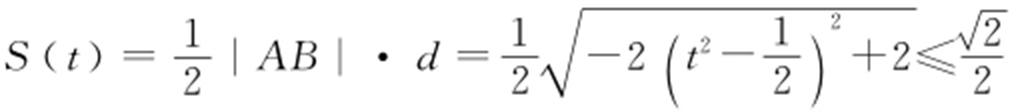 ,当且仅当
,当且仅当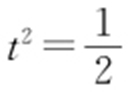 时等号成立,故△AOB 面积的最大值为
时等号成立,故△AOB 面积的最大值为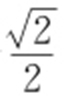 .
.
【考点 】 直线与椭圆的位置关系;点到直线的距离公式;函数的最值.
47.(1)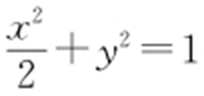 ,
,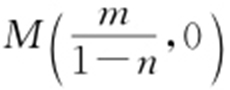 ;(2)存在点
;(2)存在点 .
.
【解析 】 (1)由于椭圆C :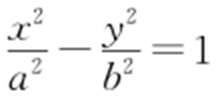 (a >b >0)过点P (0,1)且离心率为
(a >b >0)过点P (0,1)且离心率为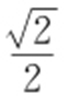 ,则
,则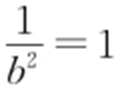 ,b 2 =1,
,b 2 =1,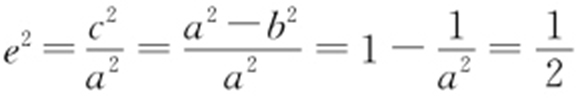 ,a 2 =2,椭圆C 的方程为
,a 2 =2,椭圆C 的方程为 .因为P (0,1),A (m ,n ),直线PA 的方程为
.因为P (0,1),A (m ,n ),直线PA 的方程为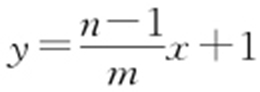 ,令y =0,
,令y =0,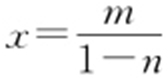 ,所以
,所以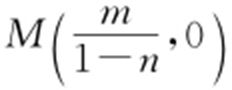 .
.
(2)因为P (0,1),B (m ,-n ),直线PB 的方程为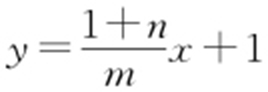 ,直线PB 与x 轴交于点N ,令y =0,
,直线PB 与x 轴交于点N ,令y =0,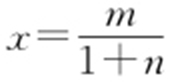 ,则
,则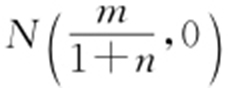 .
.
设Q (0,y 0 ),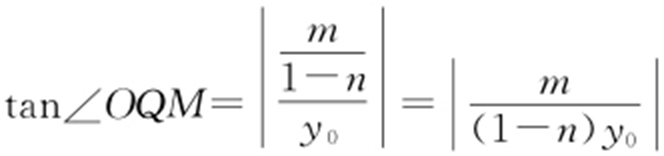 ,
,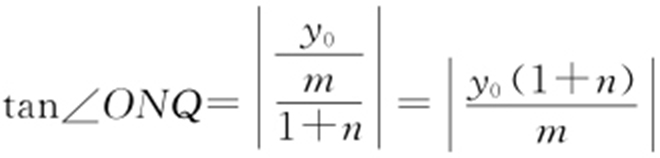 .因为∠OQM =∠ONQ ,所以tan∠OQM =tan∠ONQ ,则
.因为∠OQM =∠ONQ ,所以tan∠OQM =tan∠ONQ ,则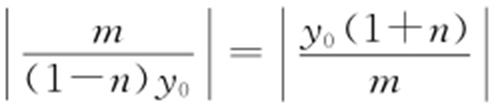 ,所以
,所以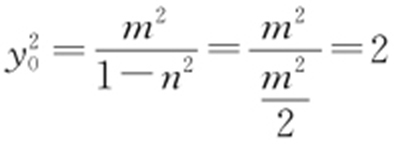 (注:点A (m ,n )(m ≠0)在椭圆C 上,
(注:点A (m ,n )(m ≠0)在椭圆C 上,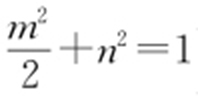 ),则
),则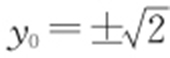 ,存在点
,存在点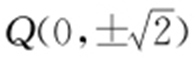 ,使得∠OQM =∠ONQ .
,使得∠OQM =∠ONQ .
【考点 】 椭圆方程;直线方程及与坐标轴的交点;存在性问题.
48.(1)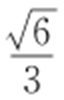 ;(2)1;(3)直线BM 与直线DE 平行.
;(2)1;(3)直线BM 与直线DE 平行.
【解析 】 (1)椭圆C 的标准方程为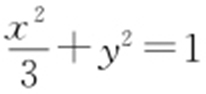 ,所以
,所以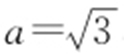 ,b =1,
,b =1,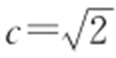 .所以椭圆C 的离心率
.所以椭圆C 的离心率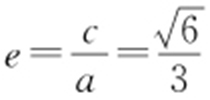 .
.
(2)因为AB 过点D (1,0)且垂直于x 轴,所以可设A (1,y 1 ),B (1,-y 1 ),直线AE 的方程为y -1=(1-y 1 )(x -2).令x =3,得M (3,2-y 1 ),所以直线BM 的斜率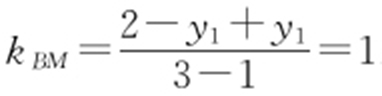 .
.
(3)直线BM 与直线DE 平行.证明如下:当直线AB 的斜率不存在时,由(2)可知kBM =1.又因为直线DE 的斜率 ,所以BM ∥DE .当直线AB 的斜率存在时,设 其方程为y =k (x -1)(k ≠1).
,所以BM ∥DE .当直线AB 的斜率存在时,设 其方程为y =k (x -1)(k ≠1).
设A (x 1 ,y 1 ),B (x 2 ,y 2 ),则直线AE 的方程为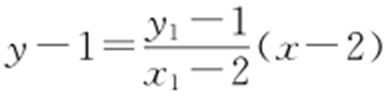 .
.
令x =3,得点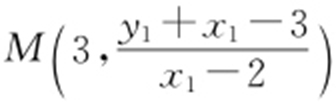 .由
.由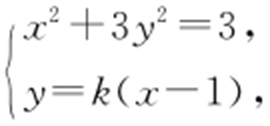 得(1+3k 2 )x 2 -6k 2 x +3k 2 -3=0.所以
得(1+3k 2 )x 2 -6k 2 x +3k 2 -3=0.所以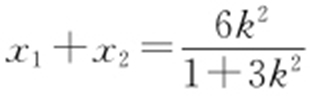 ,
,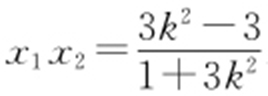 .直线BM 的斜率
.直线BM 的斜率
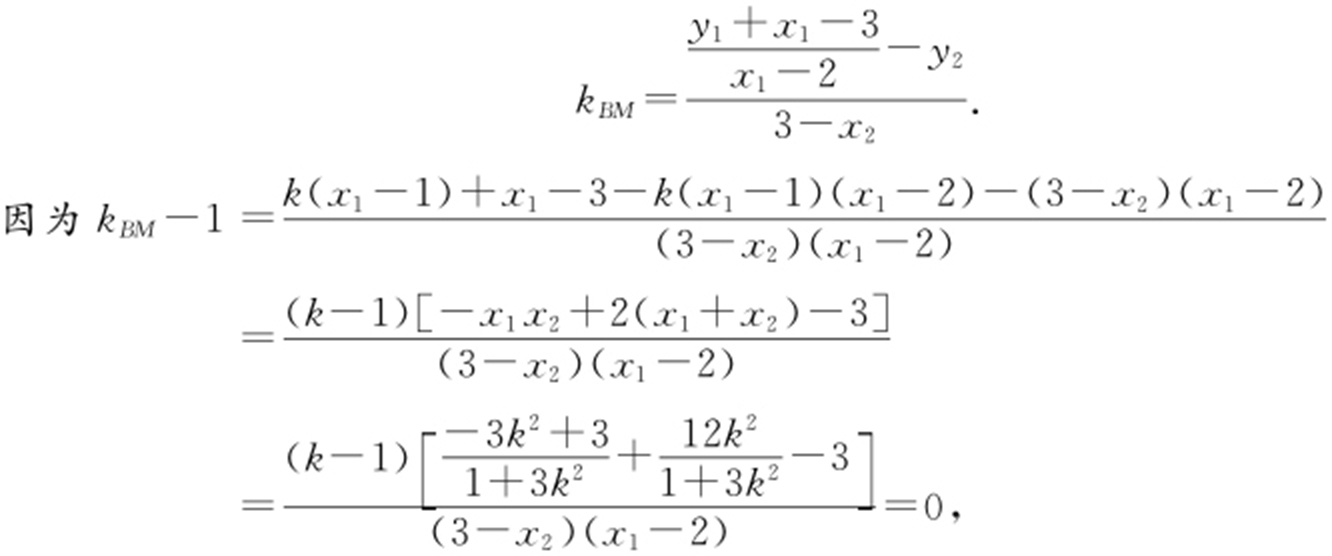
所以kBM =1=kDE ,所以BM //DE .综上可知,直线BM 与直线DE 平行.
【考点 】 椭圆的标准方程及其几何性质;直线的斜率;两直线的位置关系.
49.(1)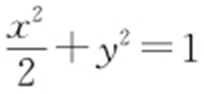 ;(2)证明略,详见解析.
;(2)证明略,详见解析.
【解析 】 (1)由题意得 ,b =1,所以
,b =1,所以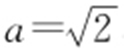 ,所以椭圆方程为
,所以椭圆方程为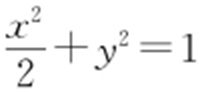 .
.
(2)由题设知,直线PQ 的方程为y =k (x -1)+1(k ≠2),代入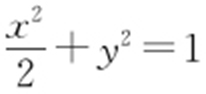 ,得(1+2k 2 )x 2 -4k (k -1)x +2k (k -2)=0.
,得(1+2k 2 )x 2 -4k (k -1)x +2k (k -2)=0.
由已知Δ >0,设P (x 1 ,y 1 ),Q (x 2 ,y 2 ),x 1 x 2 ≠0,则 ,
,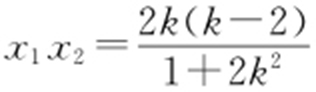 ,从而直线AP 与AQ 的斜率之和:
,从而直线AP 与AQ 的斜率之和:
【考点 】 椭圆的标准方程;圆锥曲线的定值问题.
50.(1)2;(2)①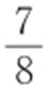 ,②
,②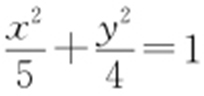 .
.
【解析 】 (1)设F (-c ,0),由已知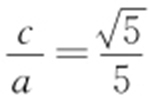 及a 2 =b 2 +c 2 ,可得
及a 2 =b 2 +c 2 ,可得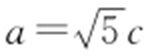 ,b =2c ,又因为B (0,b ),F (-c ,0),故直线BF 的斜率
,b =2c ,又因为B (0,b ),F (-c ,0),故直线BF 的斜率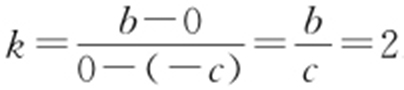 .
.
(2)设点P (xP ,yP ),Q (xQ ,yQ ),M (xM ,y M ).
①由(1)可得椭圆方程为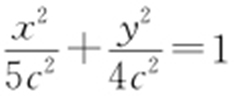 ,直线BF 的方程为y =2x +2c ,两方程联立消去y ,得3x 2 +5cx =0,解得
,直线BF 的方程为y =2x +2c ,两方程联立消去y ,得3x 2 +5cx =0,解得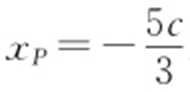 .因为BQ ⊥BP ,所以直线BQ 方程为
.因为BQ ⊥BP ,所以直线BQ 方程为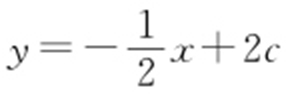 ,与椭圆方程联立消去y ,得21x 2 -40cx =0,解得
,与椭圆方程联立消去y ,得21x 2 -40cx =0,解得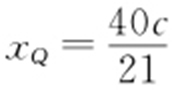 .又因为
.又因为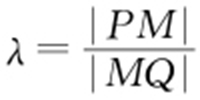 ,xM =0,则得
,xM =0,则得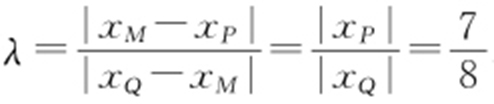 .
.
②由(1)得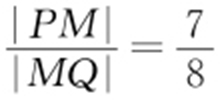 ,所以
,所以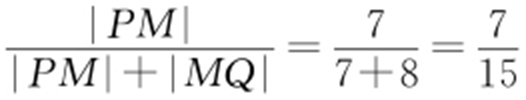 ,即
,即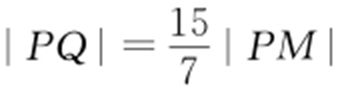 .又因为
.又因为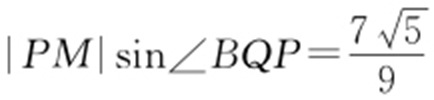 ,所以
,所以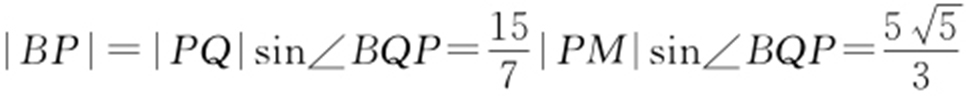 .
.
又因为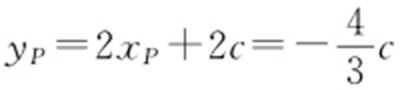 ,所以
,所以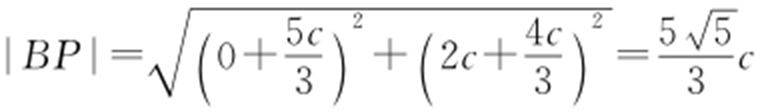 ,因此
,因此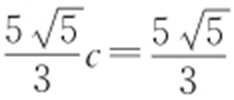 ,c =1,所以椭圆方程为
,c =1,所以椭圆方程为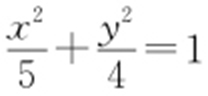 .
.

