第5章 抛物线
1.定义:动点到定点距离等于它到定直线的距离时 的轨迹称为抛物线.定点F 称为抛物线的焦点,定直线l 称为抛物线的准线.
2.抛物线的几何性质.
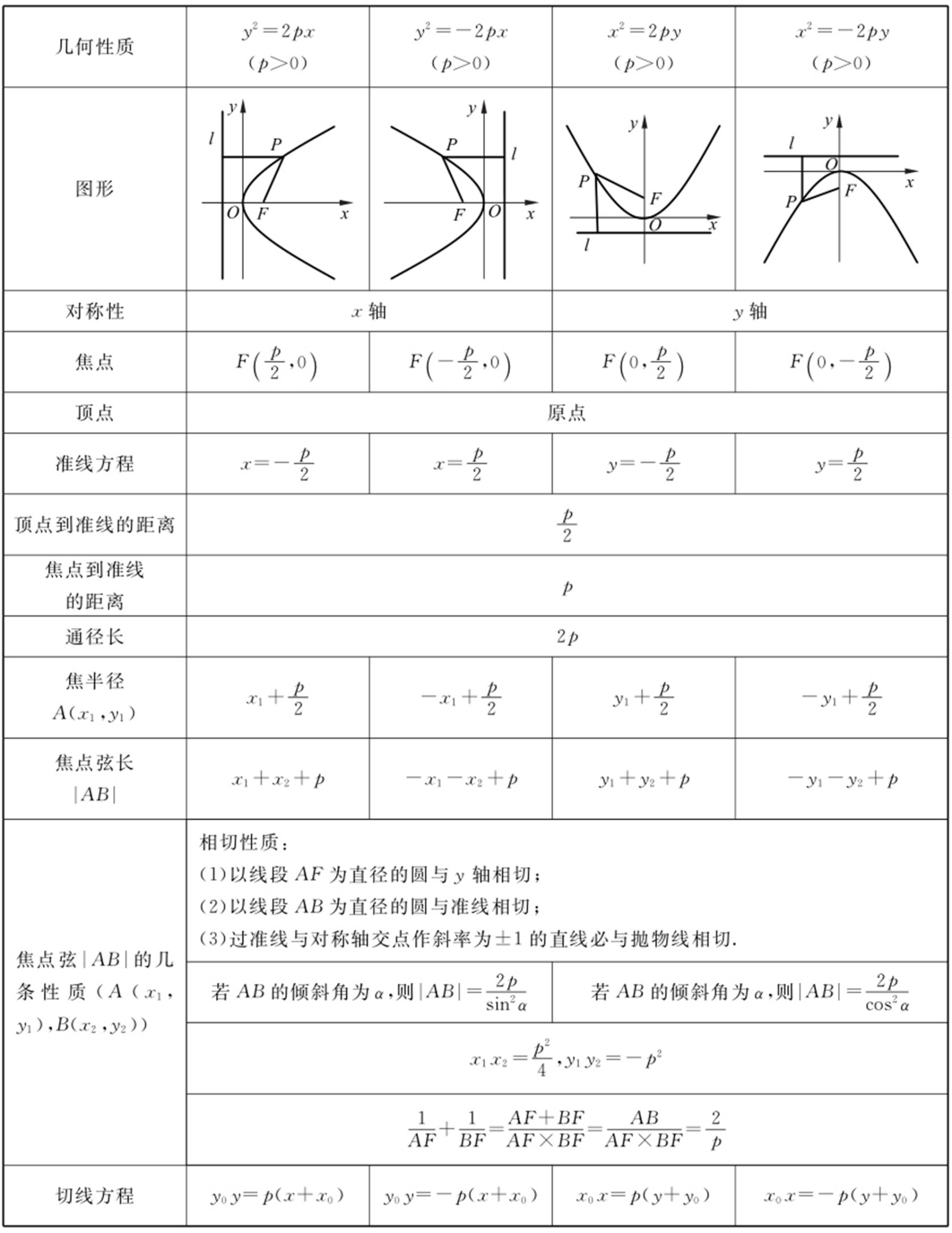
考点1 抛物线的定义
例题
【例1 】(2015·广安月考) 已知动点M 的坐标满足方程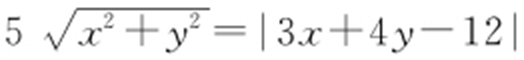 ,则动点M 的轨迹是( ).
,则动点M 的轨迹是( ).
A.椭圆
B.双曲线
C.抛物线
D.以上都不对
条件  点点距与点线距的关系.
点点距与点线距的关系.
解析 由题意可知,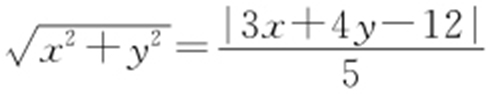 ,可知点(x ,y )到原点距离与到3x +4y -12=0距离相等,所以点M 的轨迹为抛物线.故选:C.
,可知点(x ,y )到原点距离与到3x +4y -12=0距离相等,所以点M 的轨迹为抛物线.故选:C.
【例2 】(2009·上海模考) 已知点M (1,0),直线l :x =-1,点B 是l 上的动点,过点B 垂直于y 轴的直线与线段BM 的垂直平分线交于点P ,则点P 的轨迹是( ).

A.抛物线
B.椭圆
C.双曲线的一支
D.直线
条件 垂直平分线→垂直平分线上的点到线段两端点距离相等.
解析 如图:交点P 在垂直平分线上,故PB =PM ,即动点P 到l :x =-1的距离与P 到M 距离相等,所以动点P 的轨迹为抛物线.故选:A.
总结
抛物线的定义是点点距与点线距的关系.
练习
1.(2008·北京理·4) 若点P 到直线x =-1的距离比它到点(2,0)的距离小1,则点P 的轨迹为( ).
A.圆
B.椭圆
C.双曲线
D.抛物线
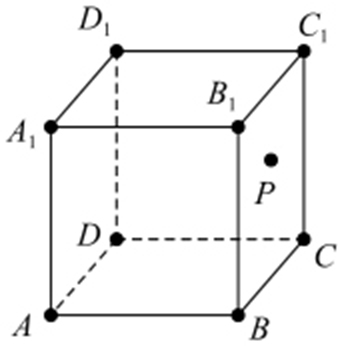
2.(2004·北京理·4) 如图,在正方体中,P 是侧面内一动点,若P 到直线BC 与到直线C 1 D 1 的距离相等,则动点P 的轨迹所在的曲线是( ).
A.直线
B.圆
C.双曲线
D.抛物线
考点2 抛物线方程及基本量
例题
【例1 】(2016·四川文·3) 抛物线y 2 =4x 的焦点坐标是( ).
A.(0,2)
B.(0,1)
C.(2,0)
D.(1,0)
条件 y 2 =2px ⇒焦点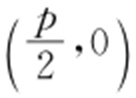 ,准线:
,准线: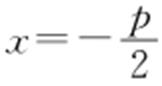 .
.
解析 2p =4,p =2⇒焦点(1,0).故选:D.
【例2 】(2013·北京文·9) 若抛物线y 2 =2px 的焦点坐标为(1,0),则p = ,准线方程为 .
条件 y 2 =2px ⇒焦点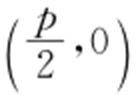 ,准线:
,准线: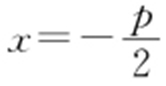 .
.
解析 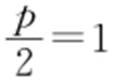 ,p =2⇒准线x =-1.
,p =2⇒准线x =-1.
总结
抛物线方程与基本量:
练习
(2014·上海文理·3) 若抛物线y 2 =2px 的焦点与椭圆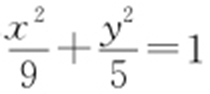 的右焦点重合,则该抛物线的准线方程为 .
的右焦点重合,则该抛物线的准线方程为 .
考点3 抛物线第一定义
例题
【例1 】(2016·浙江理·9) 若抛物线y 2 =4x 上的点M 到焦点的距离为10,则M 到y 轴的距离是 .
条件 点到焦点距离⇒点到准线距离.
解析 因为点M 到焦点距离为10,所以点M 到准线x =-1距离为10,故到y 轴距离为9.
【例2 】(2015·中山联考) 已知点P 是抛物线y 2 =2x 上的一个动点,则点P 到点A (0,2)的距离与P 到该抛物线准线的距离之和的最小值为( ).
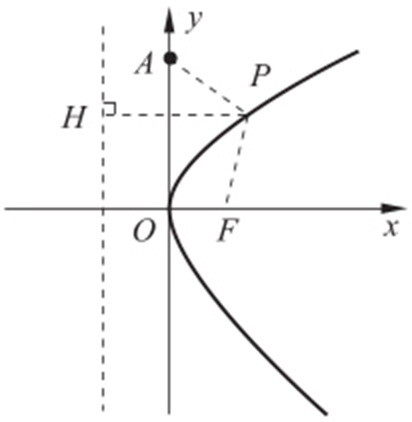
条件 点P 到抛物线准线距离⇒点P 到焦点距离.
解析 如图,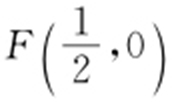 ,PA +PH =PA +PF .
,PA +PH =PA +PF .
由三角形的两边之和大于第三边,则PA +PF ≥FA ,故当A ,P ,F 三点共线时,PA +PH 最小,最小值为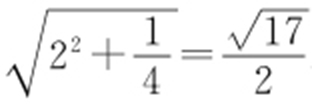 .故选:A.
.故选:A.
总结
抛物线第一定义:动点到定点的距离与它到定直线的距离相等.
练习
1.(2013·课标1文·8) O 为坐标原点,F 为抛物线C :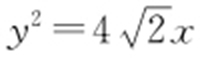 的焦点,P 为C 上一点,若
的焦点,P 为C 上一点,若 ,则△POF 的面积为( ).
,则△POF 的面积为( ).
2.(2008·江西师大附中月考) 已知点M (3,2),F 为抛物线y 2 =2x 的焦点,点P 在该抛物线上移动,当|PM |+|PF |取最小值时,点P 的坐标为 .
考点4 抛物线的焦半径和焦点弦性质
例题
【例1 】(2015·河北五校联考) 在抛物线y 2 =2px 上,横坐标为2的点到抛物线焦点的距离为3,则p = .
条件 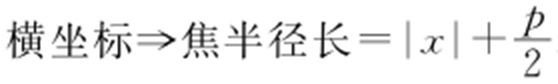 .
.
解析 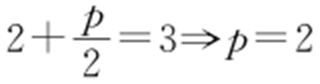 .
.
【例2 】(2013·渝中模考) P 为抛物线y 2 =2px 上任一点,F 为焦点,则以PF 为直径的圆与y 轴( ).
A.相交
B.相切
C.相离
D.位置由P 确定
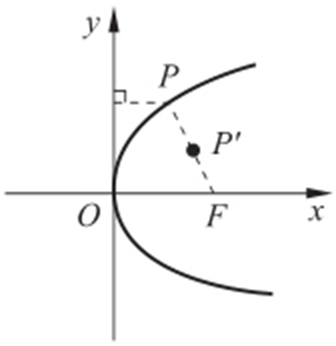
条件 以PF 为直径的圆⇒以焦半径为直径的圆与y 轴必相切.
解析 设P′ 为PF 中点,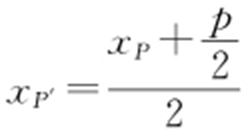 ,又
,又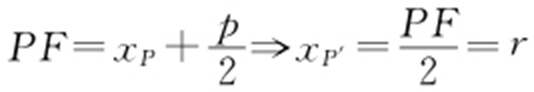 ,所以与y 轴必相切.故选:B.
,所以与y 轴必相切.故选:B.
【例3 】(2012·南昌二中月考) 一动圆的圆心在抛物线y 2 =8x 上,且动圆恒与直线x +2=0相切,则此动圆必过定点( ).
A.(4,0)
B.(2,0)
C.(0,2)
D.(0,-2)
条件 相切⇒圆心到直线距离等于半径.
解析 设圆心为P ,又x +2=0为y 2 =8x 的准线,故PF =r ,故焦点F 必在圆P 上.故选:B.
【例4 】(2012·南昌市一模) 过抛物线y 2 =4x 的焦点F 作一直线交抛物线于P ,Q 两点,若线段PF 与FQ 的长分别是p ,q ,则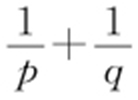 = .
= .
条件 线段PF 与FQ 的长⇒抛物线中PF 与FQ 的关系: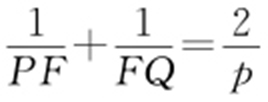 .
.
解析 方法1: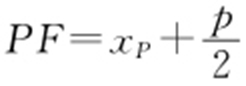 ,
,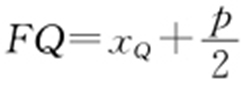 ,
,
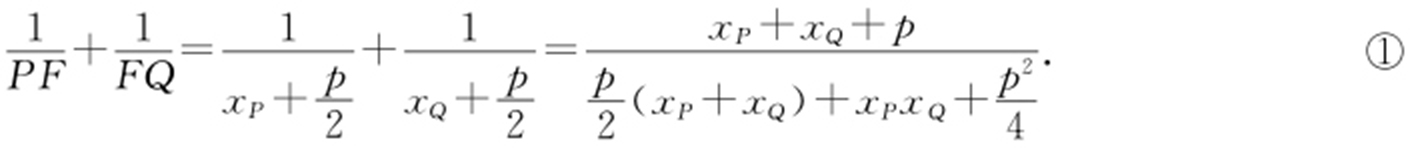
由焦点弦: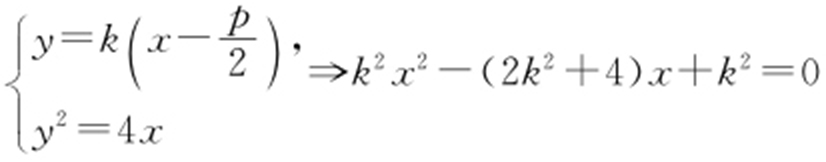 ,代入①式可求得
,代入①式可求得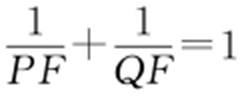 .
.
方法2:特殊值法直线取x =1,故PF =2,QF =2,所以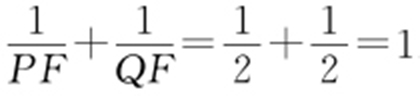 .
.
【例5 】(2011·海淀月考) 抛物线x 2 =-4y 与过焦点且垂直于对称轴的直线交于A ,B 两点,则( ).
A.|AB |=8,S △ABO =4
B.|AB |=8,S △AOB =2
C.|AB |=4,S △AOB =2
D.|AB |=4,S △AOB =4
条件 过焦点垂直于对称轴⇒通径长.
解析 依题意得,|AB |=通径长=2p =4,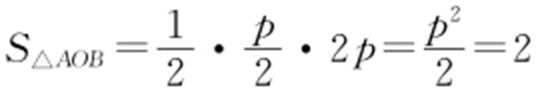 .故选:C.
.故选:C.
【例6 】(2013·南昌二中月考) 设抛物线y 2 =2x 的焦点为F ,过点 的直线与抛物线相交于A ,B 两点,与抛物线的准线相交于点C ,|BF |=2,则△BCF 与△ACF 的面积之比
的直线与抛物线相交于A ,B 两点,与抛物线的准线相交于点C ,|BF |=2,则△BCF 与△ACF 的面积之比 =( ).
=( ).
条件 
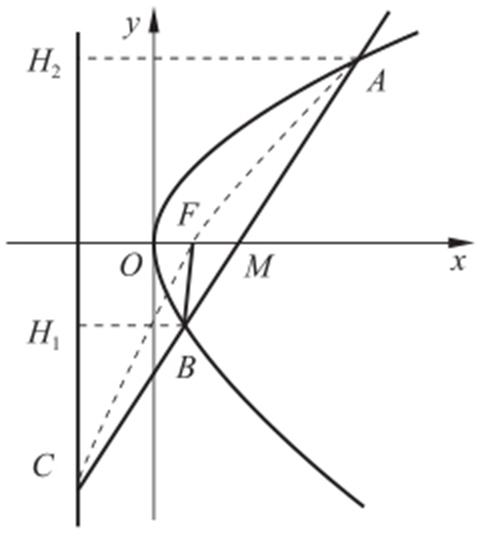
解析 如图,可选F 为顶点,故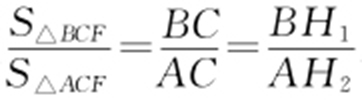 .
.
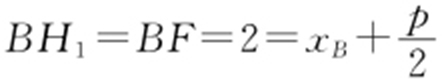 ,
,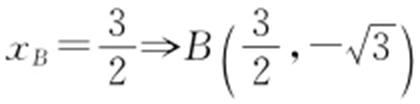 .
.
所以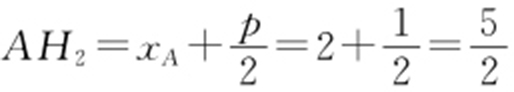 ,
,
则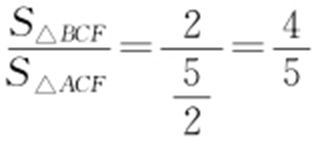 .故选:A.
.故选:A.
总结
抛物线的基本性质.
(1)焦半径长.,
.
(2)|AB |=|xA +xB |+p (y 2 =±2px )=|yA +yB |+p (x 2 =±2py ),通径长为2p .
(3)以AB 为直径的圆与准线相切,以AF (BF )为直径的圆与y 轴相切.
(4),
,
,
(y 2 =±2px ),
.
练习
1.(2010·南大附中月考) 在抛物线y 2 =2px (p >0)上,横坐标为4的点到焦点的距离为5,则p 的值为 .
2.(2009·莲塘一中月考) 过抛物线y 2 =16x 上的动点P 向圆(x -4)2 +y 2 =1引切线,则切线长的最小值是 .
3.(2014·萧山模考) 抛物线y 2 =4x 上点M 的横坐标为1,则点M 到该抛物线的焦点的距离为( ).
A.3
B.2
C.1.5
D.1
4.(2011·银川模考) 已知直线y =k (x +2)(k >0)与抛物线C :y 2 =8x 相交于A ,B 两点,F 为C 的焦点.若|FA |=2|FB |,则k =( ).
5.(2010·南昌二中月考) 过抛物线y 2 =2px (p >0)的焦点F 作直线l ,交抛物线于A ,B 两点,交其准线于C 点.若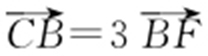 ,则直线l 的斜率为 .
,则直线l 的斜率为 .
考点5 抛物线与椭圆双曲线综合
例题
【例1 】(2013·全国文·11,理·8) 等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线y 2 =16x 的准线交于A ,B 两点,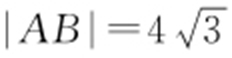 ,则C 的实轴长为( ).
,则C 的实轴长为( ).
条件 等轴双曲线⇒y =±x (渐近线),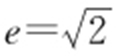 (离心率).
(离心率).
解析 准线:x =-4.设双曲线为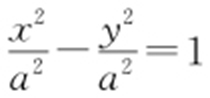 ,代入可得
,代入可得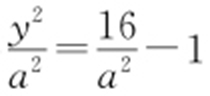 ,即y 2 =16-a 2 .
,即y 2 =16-a 2 .
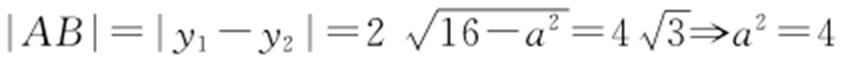 ,即a =2,则实轴长为2a =4.故选:C.
,即a =2,则实轴长为2a =4.故选:C.
【例2 】(2013·江西理·14) 抛物线x 2 =2py (p >0)的焦点为F ,其准线与双曲线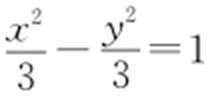 相交于A ,B 两点,若△ABF 为等边三角形,则p = .
相交于A ,B 两点,若△ABF 为等边三角形,则p = .
条件  .
.
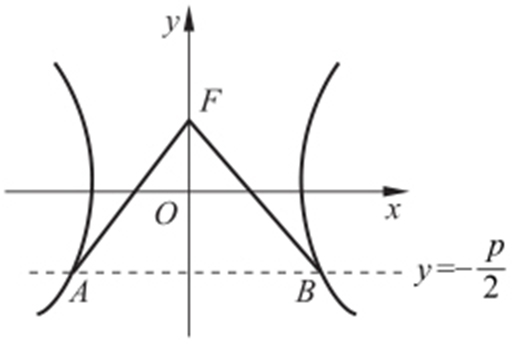
解析 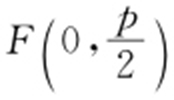 ,准线
,准线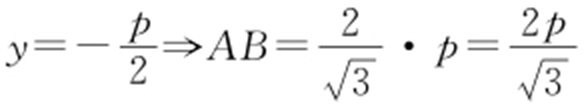 ,所以
,所以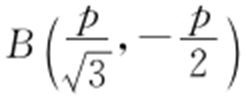 ,代入
,代入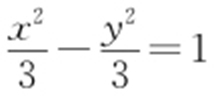 ,则
,则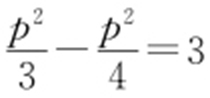 ,即
,即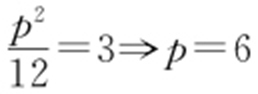 .
.
练习
1.(2014·山东文·15) 已知双曲线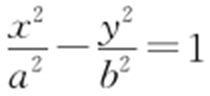 (a >0,b >0)的焦距为2c ,右顶点为A ,抛物线x 2 =2py (p >0)的焦点为F ,若双曲线截抛物线的准线所得线段长为2c ,且|FA |=c ,则双曲线的渐近线方程为 .
(a >0,b >0)的焦距为2c ,右顶点为A ,抛物线x 2 =2py (p >0)的焦点为F ,若双曲线截抛物线的准线所得线段长为2c ,且|FA |=c ,则双曲线的渐近线方程为 .
2.(2013·山东理·11) 已知抛物线C 1 :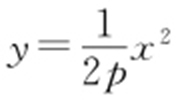 (p >0)的焦点与双曲线C 2 :
(p >0)的焦点与双曲线C 2 :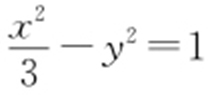 的右焦点的连线交C 1 于第一象限的点M .若C 1 在点M 处的切线平行于C 2 的一条渐近线,则p =( ).
的右焦点的连线交C 1 于第一象限的点M .若C 1 在点M 处的切线平行于C 2 的一条渐近线,则p =( ).
懂得克制,才能主宰自己的行为,切忌自以为是.别以为知道“自制心”这个字眼,就能做到自制.自制必须拿出实际行动才行.
——娴姐(刘娴老师)
请要求自己每天克制一件小事.小事上无法自制的人,面对大事更不可能自制.
——娴姐(刘娴老师)
弄清楚动机,才能找到方向,就像同一种药不见得适合于每个人的体质.同样,别人的做法也不见得适用于自己.
——娴姐(刘娴老师)
千万不要自欺欺人,不要对自己说谎,要对自己诚实,了解自己到底是个什么样的人,有什么癖好、什么想法,遇事会做出什么样的反应.
——娴姐(刘娴老师)
善良人在追求中纵然迷惘,却终将意识到有一条正途.
——《浮士德》
Get busy living or get busy dying.忙于幸福或者不觉消沉.
——《肖申克的救赎》
一万年太久,只争朝夕.
——《大话西游》
不得不承认,付不起的是心态,和钱.
——荡荡(曹灏老师)
有的时候做梦,就想停在原地,等一切变回如初,害怕着远方.是的,可能一踏出去就是错误,但只有不断寻觅,才不至枉了少年.
——荡荡(曹灏老师)
青春,是所遇到的所有,认真生活才不负真情美好.
——荡荡(曹灏老师)
时间是世上最美妙的东西,可能做得不好,但幸亏有它才有机会补过.
——荡荡(曹灏老师)









