2.1 什么是数据类型
2.1.1 “三个世界”理论
凡编程者,必须同时面对“三个世界”:问题世界、代码世界和机器世界。
从问题世界提出问题,到机器世界最终解决问题,这是一个完整的、一环套一环的过程。孤立地只看重代码不可能成为优秀的编程者。事实上,在很多情况下,正确地提出或表达问题比解决问题还要重要。
2.1.2 问题世界:“万物皆数”
“数”是对现实世界中信息的抽象和表示。古希腊的毕达哥拉斯坚信“万物皆数”。巧合的是这也是现代电子计算机对世界的理解。更巧合的是,毕达哥拉斯并不知道无理数的存在,而计算机同样也只是通过有限长度的有理数(有限长度整数和有限长度小数)来描述并模拟世界上的一切事物的(1)。
计算机的全名叫“通用电子数字计算机”(General-Purpose Electronic Digital Computer)。在这种装置中,世界万物是被编成了号码并被当成了数来记录并处理的,无论它原本是什么。数值、文字、图形、图像、声音以及指挥计算机运行的指令等,这一切都被“数字化”了,这就是“Digital”的含义,是计算机具有通用性(General-Purpose)的基础和前提。
以文字为例,当文字被编号(术语叫数字化或编码)后,就可以由计算机处理了。称呼这种编号的专业术语有很多种,有的叫ASCII码,有的叫“内码”,有的叫Unicode编码,等等。它们的区别在于对哪套文字进行了编号以及进行编号的规则。
ASCII码是计算机发展早期主要为英文字符及常用的标点符号所规定的编号。后来又出现了对汉字的编号。汉字的编号方式更复杂一些,但基本原理是一样的。在计算机内部的汉字编号写通常被叫做“内码”。再后来有人试图把世界上所有的文字符号进行统一编号,这个东西就是所谓的Unicode。
声音、图像也是同样的道理,只是编号方式更复杂,同时也不统一,这就是为什么会有许多种类型声音、图像文件的原因。
对于具体的问题来说,同样也需要进行“数字化”。比如农夫过河问题:一个农夫带了一只狗,一只兔子和一棵青菜准备渡河。农夫最多只能带其中的一样东西上船。如果农夫不在,狗会吃兔子,兔子会吃青菜。问农夫应该怎样渡河才会把狗、兔子和青菜都带过河去。
在通过计算机解决这个的问题之前,必须要做的一件事情是把问题“数字化”,必须能够用数值表达或描述出这个问题。只有这样,问题才可能被映射到机器世界中解决,因为计算机内部除了“数”以外没有别的东西。不经过这个步骤,根本谈不上编程。
由此可见,通过编程解决问题有一个前提:必须把问题中所涉及到的种种因素都抽象、归纳并表示为数值,要么是整数值,要么是小数值。否则,计算机解决不了任何问题。
2.1.3 代码世界:书写规则及含义
1.整常数在代码中的表示
当问题已经被数字化以后,必然要涉及到数在代码中的表示问题。让我们先从最简单的情况开始:十进制的123在代码中的写法。
123在代码中的写法和日常生活中的写法几乎一样。
程序代码2-1
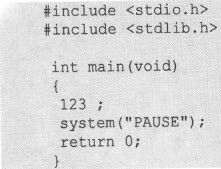
注意,这里的“123”后面有一“;”。这并不是对写123的要求,“;”并不是常数的一部分。在“123”后面写“;”是因为123无法被单独写在代码中。
2.代码中的每个数据都具有数据类型
代码中的每个数据都必须有明确的数据类型。而编译器会根据其数据类型将之翻译成恰当的机器语言。
代码中各个数据的数据类型,有的是通过代码向编译器明示的,有的是根据C语言的语法规则向编译器暗示的。前面提到的十进制整数常数“123”属于后者。
C语言规定,凡是按照十进制整数常数书写规则写出的、值在一定范围之内的整数常数都是“int”类型。这里的“int”是C语言的一个关键字,用于表示一种特定的数据类型。
C语言并没有完全明确int类型整数常数的值的上下限,只要求上限不得小于32767,具体的范围由编译器自行确定。在Dev C++中,int类型的整数常数不得超过2147483647(2)。
由于代码总是要被翻译成机器语言的可执行文件,而这个可执行文件在程序运行时将被装入内存中执行,因此就产生了另一个问题:123这样的整数常数被编译器翻译成什么样子?或者说它在内存中是什么样子的?这和计算机本身的特性有关。
2.1.4 机器世界里的“机器数”
1.计算机内部使用二进制
由于计算机没有十根手指,只有易于表示两种状态的电子元件。所以很自然,在计算机内部,“数”一律釆用二进制表示。这样不但简单可靠而且容易实现。
二进制记数的原理和十进制是一样的,都是基于数字占据不同的位置以表示不同的数值,这样一个基本的记数法则。不同之处在于,所用到的数字的个数和各个位置表示的权重不同。二进制的特点是“逢二进一”。
使用十进制时是根据0~9这10个中的数字所占据的位置表示数的真实数值的。比如,十进制的1001D(3),其第一个1和最后一个1占据着不同的位置(千位和个位),所以分别表示1个103和1个10。而在二进制的1001B中,第一个1和最后一个1分别表示的是1个23和1个20。
把十进制数化成二进制的方法是,不断地除以2取得余数,直到商为0为止。例如对于123D:


因此123D即可表示为1111011B。
把一个十进制数化成八、十六进制的方法也与此类似。
练习
分别写出123456D、654321D的二、八、十六进制形式。
2.机器数一律“整存整取”
在计算机内部,内存是数据的存储中心。内存中的数据有一个特点,就是无论流入还是流出,都是“整存整取”的。这个“整存整取”的单位就是“位组”(byte(4))
对于不同的程序运行环境而言,byte的大小可能并不相同。但C语言要求1个byte至少要能存放1.4.1小节中提到的所有“字母”。就目前最普遍的绝大多数情形而言,1个byte由8个相邻的二进制位组成。
这样,123在内存中将被放到一块由若干连续的byte构成的一块内存之中。也就是说,尽管“123D==1111011B”,存储123只需要7个二进制位,但由于123被编译后在内存中一定被存储为若干个byte,那么其位数一定是8的倍数,前面多余的位数写0,叫做前导0。
那么,123究竟被存储成什么样子呢?这完全取决于123的数据类型。由于123属于int类型,所以在机器内部按照int类型机器数的长短和格式存储。
int类型的数据在机器内部按照二进制整数格式存储。
正如同C语言没有完全明确规定在代码中十进制整数常数的具体范围一样,C语言也没有具体规定int类型数据对应的机器数究竟应该占几个byte,只是规定这种机器数长度不得少于16bit,如果按照一个byte为8bit计算,就是不得少于2byte。在Dev C++中,int类型数据对应的机器数为4byte。
这样也就不难发现,问题世界中抽象出的常数一百二十三,在C源代码中要写成“123”,而编译后在内存中对应的则是0000 0000 0000 0000 0000 0000 0111 1011这样一个机器数,如图2-1所示。
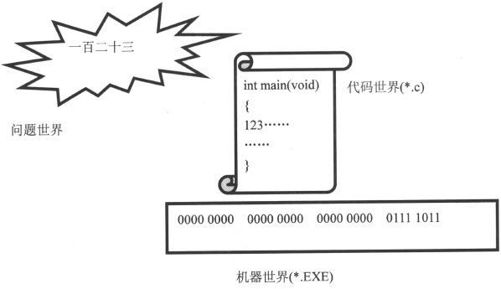
图2-1 3个世界中的数据
3.常量的概念
前面提到的写到代码中的常数123,尽管被编译后意味着一块4byte的内存里的机器数,但是C代码并没有改变这块内存中数据的手段,甚至没有探明这个机器数位置的技术手段(5)。这种在代码中无法改变的常数被叫做“常量”(Constant)。
常量一般对应于我们自己在纸上用笔运算时需要记住的(也可能是记在头脑中)且一直保持不变的量。比如在计算圆的面积时的圆周率π。
C代码中的常量都必须按照特定的格式要求书写。C语言对代码中的十进制常量的书写要求如下。
(1)不可以有数字0~9以外的任何符号。
(2)开头一位不可以是0。
从这两条规则中可以发现在代码中只可能写出正的十进制整数常数。此外不难想到的是十进制格式的int类型常量的值显然有一个限度,因为对应的机器数的长度是有限的。
2.1.5 输出问题
编译器把代码中的常量“123”翻译成了内存中的二进制数“0000 0000 0000 0000 0000 0000 0111 1011”。本质上其实是把代码中的1、2、3这3个连续的文字序列翻译成了机器内部的二进制数。如果希望把“0000 0000 0000 0000 0000 0000 0111 1011”在屏幕上输出,就必须进行一次反向的转换,亦即把二进制数再次转换成恰当的文字序列。因为编译后在内存中只有“0000 0000 0000 0000 0000 0000 0111 1011”而并没有1、2、3这几个文字,而在屏幕上却只能显示文字。
这就是说,二进制数“0000 0000 0000 0000 0000 0000 0111 1011”必须被转换成文字序列才能被输出到屏幕上。这个转换和输出也可以通过调用Printf()函数完成。方法如下:
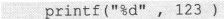
这里的%d叫做转换说明(Conversion Specification),转换说明总是以“%”开始,后面可以跟适当的转换说明符(Conversion Specifier)。这里“d”表示的意义是把一块4byte中的内存内容当做一个二进制整数转换成对应的十进制格式的字符序列并插入“%d”中%d所在的位置输出。被转换的二进制整数写在格式控制字符串之后,两者之间用“,”分隔。
当然,也可以转换成其他格式。比如%X(或%x)表示的是转换成对应的十六进制格式的字符序列。例如:

在标准输出设备上的输出如图2-2所示。

图2-2 转换为十六进制输出
如图2-3所示,详细说明了这种转换和输出的含义。
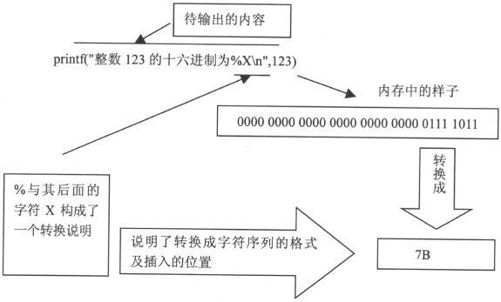
图2-3 转换说明的含义
也可以对多个数据进行转换输出,如下所示:
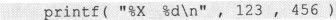
2.1.6 计算2的1到10次幂
有了前面的知识,现在就可以编写一些更复杂的程序了。在完成本题目之前还需要补充一点C语言的知识。
C语言规定,一个int类型的数据可以与另一个int类型的数据进行乘法运算,得到的结果也应该且必须是int类型。此外C语言用“*”表示乘法运算(数学中的乘法运算符号“×”不属于C语言的基本字符)。C语言不认为“乘方”运算是必须的,所以在C代码中乘方只能通过乘法来实现。
这样2的2次幂在代码中就可以通过“22”求得,而由于“22”也是int类型,所以也可以调用printf()函数输出。
例题:计算2的1到10次幂并输出。
程序代码2-2

屏幕输出如图2-4所示。

图2-4 计算2的1到10次幂并输出
这段代码似乎没有什么明显的问题。然而,在源代码中突兀地出现常量,这一行为被很多有识之士认为是一种不良的编程风格,是缺乏编程修养的表现。因此在编程时,一般的做法是根据常数所代表的含义为常量取个有意义的名字,在源代码中只用这个有意义的名字而避免编写直接露骨的、赤裸裸的常量。正如我们写圆面积的计算公式时总是用π表示圆周率一样。
下面将介绍如何为常量取名等进一步改进代码质量的技巧。
2.1.7 代码质量的改进
1.标识符
由程序编写者所取的名字都叫做“标识(6)符”(Identifier)。
C语言的语法对标识符提出的语法要求是:由字母、下划线(_)、数字组成,不能以数字开头(7)。
从代码质量、程序可读性及编程修养的角度对标识符提出的要求是:“知意简明”。其中,“知意”毫无疑问更重要些。当然,这不是C语言强制性的要求。许多不注意编程修养的人活得也很好。正如很多人不注意个人修养一样,法律是管不到他的。这是一个境界的问题。
一般来说,由低到高,编写代码的境界依次是:机器能懂,自己能懂,别人能懂。
所以,自己懂得自己命名的标识符的含义并不是一个很高的要求。不要动不动就是a、b、c或a1、a2、a3那样地乱取名,这如同给自己的子女取名为小一、小二、小三一样粗俗。
在程序中使用英文单词取名并不应当受到指责,假如你的英文足够好的话。但如果你的英文尚不敢亮给你的英文老师看的话,建议你还是使用汉语拼音,毕竟你编程的水平和你的英语水平毫无关系。笔者曾见过一段代码,一本正经地把“体重”和“身长”分别取名为“weight”和“feet”,也见识过一段关于素数的代码中居然出现了leap(闰年)这个标识符的例子,结结实实且前所未有地把编程提高到了幽默的境界。
标识符的长度是受限制的,C99要求编译器至少要容许63个有效字符,C89是31个。各个编译器也可能有自己的限制,请留心一下编译器的使用说明。
一般情况下,重名是不容许的,这会带来混乱。但在一定条件下重名是容许的。但是容许并不意味着鼓励。笔者见过一些考试题目,考的就是重名的问题,然而那种写法本身就是一种恶劣的编程方式,因此笔者对于这种考题的目的也是一直非常不解。
在这里忠告诸位读者,尽量不要重名,除非是在程序的不同的区域内。这就如同在两个不同班级上有同名的同学一样,通常不会带来什么麻烦。如果在同一个班级发生重名,通常“后果很严重”。
优秀的软件企业一般有自己的命名规范,如果你在企业工作,你应该遵守你本企业的规范。本书釆用的风格是“见名知意”,即釆用了汉语拼音。然而见名知意与简洁通常是矛盾的,有时必须在两者之间进行权衡与折中,所以例外的情况是特别常用的如循环变量用i或j,临时变量用tmp这样简单的名字而不是汉语拼音。本书无意把这种风格强加于任何人,只希望能达到使代码更具有可读性同时能使读者建立起命名规范的意识的目的。
练习
1._bool、_complex是C语言的关键字吗?能否作为代码中的标识符?_Imaginary呢?
2.下列符号那些可作为C语言标识符?
3M MAEN var int m-n 2_bool type a_3 exp sin printf_23
2.编译预处理命令#define
可以通过编译预处理命令为常量取名。在使用该常量之前(更通常的惯例是在源代码最前面)写上如下一行:
define 常量的名字 常量的值
其中,常量的名字是编程者为该常量所取的名字,这是一个标识符。这种用标识符表示的常量有时被叫做符号常量(Symbolic Constant),以区别于那些直接写出的赤裸裸的常量。为了区分这种符号常量与变量(通常小写),习惯上符号常量用大写字符命名。不要以为这种良好的风格与习惯是无所谓的事情,等到代码乱到一团糟的时候再想改正不良习惯就有些来不及了,而且改习惯的代价很高。编写代码,应该“勿以善小而不为,勿以恶小而为之”。
#define预处理命令的含义大体相当于文字处理软件中的“査找”与“替换”:编译器将在代码中査找常量的名字然后替换为常量的值。在这个动作是在编译之前完成的,因此实际被编译的代码是和不做这个预处理而只在代码中直接写那些赤裸裸的常量是一样的,但写具有常量含义的名字比直接写常量的值的代码更加具有可读性。下面示例是对程序代码2-2的改写版本:
程序代码2-3

这种写法还有另外一个好处,只要稍做改动再重新编译,很容易便可计算出其他的数的幂。比如要计算3的各次幂,只要把#define DS 2中的2改为3就可以了。
3.注释
在程序代码2-3中出现了一种新的代码成分——注释,就是写在/**/之内的部分和写在//之后直到该行结束的部分。在C99标准出现之前只容许第一种写法,从C99开始也容许了后一种写法。后一种写法最早出现在C++语言中,并且在C99之前就早已经被许多C语言的编译器接受了。
这两种写法的主要区别是后一种只能写单行的注释——从//处到行末。此外要提到的一点是前一种注释不可以嵌套。
对于编译器来说,注释部分的内容是不存在的——在编译预处理之前这部分内容就已经被删除并替代为空白字符了。因此,注释是给人看的,是为了提高代码的可读性,是一种备忘录性质的东西——既针对别人,也针对自己。只要代码不是一次性使用的,就一定要有注释。勤于在代码中写注释,是一种编程修养和素质。尽管注释的内容对于编译器无效,但注释的意义一点也不次于对于编译器有效部分的代码。
这里再介绍一些简单的事实。
■ 许多高手的代码中,注释的比重多于可执行部分的代码。写可执行部分的代码,只是他们工作的一小部分而已。
■ 许多高手有这样写代码的习惯,先写注释,再写代码。注释写完之后,基本上就已经胸有成“序”了。
好,事实我就讲这么多,写不写注释以及是否主动自觉地养成写注释的习惯,还要看读者自己的觉悟。
练习
编程计算2的11到20次幂并输出。
4.代码的不足
尽管如今的代码质量已经有了很大的提高,但是代码给人的感觉依然是有些臃长啰嗦。如果用这种办法计算2的10到20次幂并输出的话,代码会庞大得令人有些难以忍受。
造成这种状况的原因是在代码中出现了不断的重复计算,比如,在求2的2次幂时计算了一次“22”,但在后面计算2的其他次幂的时候依然需要重复计算这个结果。如果能够“记住”“22”的结果,那么在后面显然就不需要重复计算了。
事实上当我们自己计算这个问题的时候,总是得到一个答案后立刻记住,并根据记住的这个答案求下一个答案的。比如,2的一次幂是2,根据这个2的一次幂的结果我们可以计算出2的2次幂是4,然后根据记住的这个4可以知道2的3次幂是“2×4”得8,再根据记住的这个8可以算出2的4次幂是“2×8”得16……。很显然在这样的计算过程中,只需要记住前一次的结果,就可以得到下一个结果,不需要每次从头重新开始计算。但这样的前提是每次都能“记住”运算结果。
