8.4　位运算

在前一小节中，我们利用union类型成功地实现了对double数据的分解与分析。迄今为止，我们对数据的所有操作至少都是以byte为单位的。如果希望对数据的某个位进行操作，只能通过“绕弯子”的方法迂回进行。本小节介绍的位运算可以实现以位为单位对数据操作的运算，对位的操作更加直截了当。

由于计算机使用的是二进制，所以对于位运算来说，熟悉二进制是必然的要求和前提。在进行下面的阅读之前，请确信已经熟练掌握了二进制的知识。

此外需要事先了解的是，所有的位运算的运算对象只能是整数类型。当然，对于有些整数类型可能存在一元转换，比如char类型在运算之前会被转换成int类型。

8.4.1　位运算符

1．按位取反——“～”

“～”运算的运算结果是计算对象的各个位相反数的值。即：如果运算的对象的某位为1，则计算结果中对应的位为0；如果运算的对象的某位为0，则计算结果中对应的位为1。例如，“～4042322160U”，由于4042322160U的二进制形式为“1111 0000 1111 0000 1111 0000 1111 0000”，“1111 0000 1111 0000 1111 0000 1111 0000”进行“～”运算得到的结果为“0000 1111 0000 1111 0000 1111 0000 1111”，即252645135U。

“～”是位运算符中唯一一个一元运算符，它的优先级和结合性与一元运算“＋”、“_”一样。

显然，可以利用“～”很容易地求出一个负整数的反码。下面的程序代码演示了这种应用。

程序代码8-10

对于绝大多数情况，这个代码是正确的。但请注意，对于最小的int类型的数，代码是存在问题的。因为在进行“-zs”运算时存在溢出。

练习

重新编写程序代码8-10，使之在输入最小的int值时也正确。

2．按位与——“&”

“&”是一个二元运算符，其运算被定义为对两个运算对象逐位检查，当两者相应的位皆为1时运算结果对应的位上的值也为1，否则结果对应的位为0。例如“2155914982U & 2095755980U”，由于“2155914982”和“2095755980U”的二进制分别为“1000 0000　1000 0000　1010 0110　1110 0110”和“0111 1100　1110 1010　1011 0010　1100 1100”，故

的值为：

“0000 0000 1000 0000 1010 0010 1100 0100”。如果用十进制输出的话，即“8430276”。

“&”的优先级为8，低于“==”及“!=”但高于“&&”，结合性为从左到右。

这个运算常常用于检查某个位上的值。比如，如果“&”的一个运算对象为二进制的“0000 0000　0000 0000　0000 0000　0000 1000”时，可以用来检查一个4byte长的数据的右面第4位（b3⁽³⁾）是否为0。因为“0000 0000　0000 0000　0000 0000　0000 1000”与另一运算对象进行“&”运算时，结果相当于把另一运算对象的其他位都变为0。仿佛“0000 0000　0000 0000　0000 0000　0000 1000”把另一运算对象全部用“0”“遮盖”住，只留了一个“观察缝隙”。

这个运算也可以用来“观察”另一运算对象的若干位，比如“0000 0000　0000 0000　0000 0000　0000 1100”可以用来只“暴露”另一运算对象的b2、b3位而把其余的各位变成“0”。

从另一个角度看，这个运算可以把某个运算对象的个别位设置为0，其余的各位不变。比如“1111 1111　1111 1111　1111 1111　1111 0011”可以用来得到把另一运算对象的b2、b3位设置为0而其余的各位不变的结果。

对于一个整数类型的值x，如果不存在类型转换的话，那么x&x显然还是x，而～x & x显然为0。

使用这个运算，上一小节中输出一个int值的二进制的函数定义可以改写为：

程序代码8-11（片段）

显然这时不需要做“n%=e_n;”这个除法运算了。

“&”可以与赋值运算符构成复合赋值运算符：“&=”。这个运算的优先级和结合性与“=”一样。表达式“a &=b”的含义是“a=a & b”。

事实上，除了按位取反运算外，其余5个位运算符均可与赋值运算符一起，构成复合赋值运算符：“&=”、“|=”、“^=”、“<<=”、“>>=”。后面对此将不再详述。

3．按位异或——“^”

和许多初学者的“想当然”不同，“^”在C语言中并不表示乘方运算而表示按位异或运算。其运算规则和“按位与”的规则的区别只在于，当两个操作数相应的位一个为0而另一个为1时，运算结果对应的位上的值为1，否则结果对应的位为0。例如：

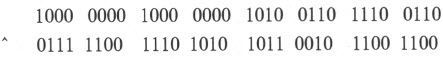
的值为：

“1111 1100 0110 1010 0001 0100 0010 1010”。

“^”的优先级为7，结合性为从左到右。

这个运算可以实现把某个运算对象的个别位“反转”而其余各位不变的效果。比如“0000 0000　0000 0000　0000 0000　0000 1000”可以用来得到只把另一运算对象的b3位设置改变的结果。

再比如，对于：

“c=c^0X20;”可以把c改成小写字母a的ASCII码。如果再次执行“c=c^0X20;”，则又把c改成了大写字母A的ASCII码。

对于一个整数类型的值x，x^x显然为0，x^0依然得到x，而～x^x显然是一个各位皆为1机器数的值。

“^”运算可以用来实现交换两个整数类型变量值的算法，而不需要借助另一个中间变量。假设运算过程中不存在类型转换，那么对于两个整数类型变量x、y，经过下面运算后

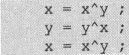
就可以实现x、y值的交换。

这个算法的原理就是“^”运算也符合类似加法或乘法那样的交换律和结合律（“&”、“|”运算也具有这样的性质），而且如前面提到的，x^x为0，x^0依然得到x。

尽管这种算法具有不需要另一个中间变量的优点，但由于难于被人理解，所以并不常用。毕竟，多数情况下代码的可读性是仅次于正确性的代码质量标准。

4．按位或——“|”

“按位或”运算的运算规则和“按位与”的规则的区别只在于，相应的位皆为0时运算结果对应的位上的值为0，否则结果对应的位为1。

例如：

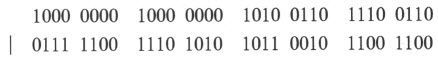
的值为：

“1111 1100 1110 1010 1011 0110 1110 1110”。

这个运算可以把某个运算对象的个别位设置为1，其余的各位不变。比如“0000 0000　0000 0000　0000 0000　0000 1100”可以用来得到把另一运算对象的b2、b3位设置为1而其余的各位不变的结果。

5．左移——“<<”

左移是一种二元运算符，其运算规则是将“<<”的左操作数的机器数的值向左移动若干位，“<<”的右操作数给出的是移动的位数。移出数据边界的各位被舍弃，缺少的各位补0。例如，“3<<2”这个表达式，由于“3”的机器数是“0000 0000　0000 0000　0000 0000　0000 0011”，向左移动2位的结果是“0000 0000　0000 0000　0000 0000　0000 1100”。

显然，这个运算可以用来很方便地产生一个特定位为1的值。比如，如果需要一个b3位为1，其余各位为0的值，显然可以用“0x1<<3”得到。

“<<”的优先级和结合性参见本书附录。

“<<”的操作数必须是整数类型，两个操作数分别进行普通的一元类型转换，结果为左操作数转换后的类型。若右操作数的值不小于左操作数类型转换后的位数或为负值时，运算是未定义行为。

下面用位运算的方法重新思考一下前面的一道例题。

练习

某地发生一起凶杀案，凶手是a、b、c、d、e、f中某一人。L说不是a就是b，M说决不是c，N说案发时a、b都不在场。已知L、M、N中只有一人正确，请问谁是凶手。

如果用一个数据中的各个位为0或1表示a、b、c、d、e、f是否为凶手，显然只需要6位就表示出答案。这样只需要一个int类型的变量就足够了。

由于题目条件是只有一个凶手，所以可以很容易地通过移位运算列举出所有一个凶手的各种可能。

程序代码8-12

运行结果如图8-5所示。

图8-5　“左移”程序代码输出

显然，这种解法比前面那种多重循环嵌套要简洁得多。

左移运算在一定条件下和乘以2等价。由于移位运算的速度一般比乘法运算快，所以在特别要求速度的情况下，有时可以代替乘以2的运算。

6．右移——“>>”

右移运算的方向与左移相反。优先级和结合性、对操作数的要求及类型转换的规则和左移运算都一致。不同之处在于，在被移出的空位上是否补0。

C语言规定，如果被移位的数据的最高位不表示负号，那么在左面移出的空位上补0；如果最高位表示负号，那么补0或补1由编译器决定。

这就是说，对于一个无符号整数类型或正的有符号整数类型数据，高位一定是补0；而对于一个负的有符号整数类型数据的右移运算结果取决于具体的编译器。显而易见右移运算不一定是可移植的。

下面代码中shuchu_erjinzhi()函数的功能是按照二进制格式输出一个int的值。

程序代码8-13

运行结果如图8-6所示。

图8-6　“右移”程序代码输出

其中的表达式“m=(unsigned)n >> 1”中的“(unsigned)n”就是考虑到了“>>”运算的不可移植性而做出的完善和修正。

8.4.2　更节省空间的筛法

在7.3.3中介绍过如何用筛法求素数表，当时代码采用的是用数组记录各个正整数，然后“划去”非素数（将非素数改写为0）。这种解决方案占用的内存空间较大，对于求比较大范围的素数表是不合适的。

记录一个正整数是否为素数，实际上只需要一个0或1就足够了。所以更节约空间的做法是，用二进制数的每一位的值表示一个正整数是否为素数。

1．问题及解的表示

假如问题的要求是，求1到ZDZ（最大值）范围内的素数表（为描述方便，ZDZ取为CHAR_BIT⁽⁴⁾的倍数）。那么显然只要“ZDZ/CHAR_BIT”个char大小的连续内存空间就可以满足要求。然后从低到高，每一位对应一个正整数，并用这位的值记录一个正整数是素数（SHI，1）或不是素数（FOU，0）。由于最初并不知道哪些正整数不是素数，所以这些位的初始值一律设置为1。然后再按照筛法逐个划去非素数（对应的位置为0），最后剩下的依然为1的各位所对应的正整数就是1到ZDZ范围内的素数，如图8-7所示。

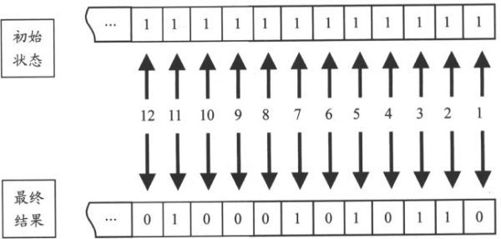
图8-7　问题及解的表示

在这种解决方案下，问题的解显然可以用下面的数据类型存储并表示：

unsigned char ssb[ZDZ/CHAR_BIT];

而且这个数组中的每个元素都应该赋初值为255。在代码中，这可以由sz_cz()函数对每个数组元素赋值简单地实现。

2．求解过程

由于是用位记录对应的数是否为素数，所以显然算法用位运算实现更为方便。

对于正整数n，对应的位显然是数组中的第(n-1)/CHAR_BIT个元素的第(n-1)% CHAR_BIT位。

将某个unsigned char类型的变量uc的第i位写为0可以经过下列步骤实现。

（1）通过“1 << i”求得一个第i位为1其余各位为0的值。

（2）对该值取反，“～(1 << i)”可得到一个第i位为0其余各位为1的值。

（3）通过“uc &=～(1 << i)”使得uc的第i位为0，其余各位不变。

读出某个unsigned char类型的变量uc的第i位的值与此类似，请自己分析。代码主要部分的N-S图如图8-8所示。

图8-8　N-S图

3．代码

代码中的main()主要有两个功能：根据筛法制作素数表；测试。函数void zhi_0(unsigned u，unsigned char ssb[])的功能是，把ssb中对应于正整数u的位设置为0；函数int shi_ss(unsigned u，unsigned char ssb[])的功能是，通过读ssb中正整数u的对应位的值并根据这个值是否为0判断u否为一个素数。

程序代码8-14

运行结果如图8-9所示。

图8-9　节省空间的筛法

代码中出现了两次求下标和位数的语句，实际上这是应该避免的。这可以通过一个函数实现。但由于这两句求的是两个值，所以需要建立一种新的包含这两个成员的struct类型。函数返回这种struct类型，就可以实现同时返回两个计算值的效果。请自己编写代码完成这个改进。

除了以上讲到的，位运算在许多其他问题中也有很广的应用。比如文件的加密和解密、图像处理、数据压缩以及关于计算机底层的操作等方面。但解决这方面的问题首先需要了解相关的背景知识，这已经超出了本书的范畴。

位运算一般都有直接对应的机器指令，所以执行的速度比较快。在一般的应用程序中，有时可以达到使代码更为简洁、程序更为高效的效果。