7.4 数组名做实参
7.4.1 数组名的值究竟是什么
作为右值表达式,数组名确实有个值。但和基本类型变量不同的是,数组名的值不是程序编写者通过代码赋予的,而是编译器在编译的时候给予的,而且这个值就是存储数组的内存单元的起始内存单元的编号,也就是一个地址。通常所说的数组名的值是数组的首地址就是这个含义。如图7-3所示,显示了数组名的值与数组的存储之间的关系。

图7-3 数组名的值与数组的存储
图中,假设数组的4个元素被存储在从1232H到1241H(2)这16个字节中,那么数组名bjs的值就是1232H。
下面对数组名和基本类型的差异做细致的比较,对于如下定义:
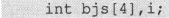
bjs:有值,且有确定含义,这个值是由编译器分配的,不可以通过代码改变,因此bjs可以被视为一个“常量”。
i:有“垃圾值”,这个值没有任何意义,可以通过赋值等手段改变i的值。
为什么要如此关心数组名的值呢?因为在函数调用时首先要计算实参的值,之后这个值还将成为对应的、相同类型的那个形参的初始值。
7.4.2 对应的形参
函数调用时使用数组名做函数实参,由于这里的数组名是一个右值,类型为:
数组元素的类型[]
因此对应的形参的类型也应该如此。
数组元素的类型[]这种类型是一种不完全类型(Incomplete Type),它的不完全性体现在无法用它定义变量(因为编译器不知道数据的长度,无法为这个变量分配内存空间),但可以用来描述一种类型或说明一个标识符的类型。不完全类型只在有限的若干种情况下使用(3),除了在函数原型中使用之外,也被用来说明形参的类型(4)。
也就是说,如果使用数组名bjs做实参,那么对应的形参的类型应该是int[];如果对应的形参取名为bjs,那么对应的形参的声明应写为int bjs[]。
7.4.3 调用原理
下面的代码是一个原理性演示代码,作用是把只有一个元素的a数组的元素的值加1。这并不是一个很正规的代码,这里只是用来说明函数名作实参时函数的调用是如何实现的。
程序代码7-6


在程序的main()函数中,a[0]是一个由数组名a、下标0及运算符[]构成的表达式,这个表达式的意义是明确的,就是a数组的第一个元素(有时表示这个元素的值,有时表示这个元素所在的内存)。
在发生调用jia1后,由于形参b具有了与数组名a相同的值,因此在函数jia1()中,b与下标0及运算符[]构成的表达式b[0]与a[0]是完全一样的表达式。由于这个缘故,在函数jia1()中b[0]表示的是和main()函数中同样的含义——a数组第一个元素的值或这个元素所在的内存。
这就是数组名作为实参时,函数调用的基本原理:两个相同类型的值相同,做相同的运算表示的含义也自然相同。
与前面的自定义函数相比,这段代码有一个特别的不同寻常之处,那就是调用jia1()函数改变了main()中的a数组的数据。
7.4.4 不可以只有数组名这一个实参
由于数组名的值中没有任何关于数组元素个数的信息(从对应形参类型的描述中也可以看出这一点),所以在使用数组名的值作为实参时,通常还应该有另外一个实参,就是这个数组元素的个数。
例题:有一数组,共10个元素,其值分别为9、6、3、6、3、5、8、1、3、5,通函数求这个数组中所有元素的和并输出。
程序代码7-7

这是一个简单的题目,题目的主要目的是演示如何通过函数实现对数组的操作。要点有如下几点。
(1)数组名做函数的实参,函数声明中对应类型的写法。(数组定义为“int a[10];”,对应的类型为“int[]”。)
(2)可以在定义时给数组各个元素或部分元素一个初始值。
(3)数组名做函数的实参,函数定义中对应的形参的类型写法。(数组定义为int a[10];对应的形参类型应该写成int p[],注意这里是将int和[]分别写在形参前后来描述形参的类型的。)。在形参后面的[]里面不应写任何值,因为写了也没有任何意义,编译器会忽略这个值的。
(4)数组名作为实参,一般总是伴随着另一个实参——数组元素的个数,来告诉函数这个数组一共有几个数组元素。通过表达式“sizeof a[0]/sizeof a[0]”来计算数组元素的个数,要比直接写10更专业、更不容易出错,且无论数组有几个元素,这个表达式总是正确的。
7.4.5 const关键字
7.4.3小节中的代码揭示了这样一个事实:数组名作实参时,被调用函数可以改变调用函数处所定义数组中的元素的值。
以7.4.3小节中的代码为例,由于形参b的值等于实参a的值,那么就可以用jia1()函数改变main()中定义的数组a的元素的值。这在函数不是以数组名为实参、而是以基本的数据类型为实参的时候不会发生,因为形参的初始值只是实参的一个副本。然而数组名a的值的副本却是可以改变数组a中元素的值的!这是因为a或b这样的值与一个整数做[]运算得到的就是数组元素——既可以是这个元素的值也表示这个元素所在的内存。有的时候希望这样的事情发生(比如要求一函数输入数组元素的值),但在另一些时候是不希望发生的(比如要求一函数输出数组元素的值)。
在明确希望变量不被改变的情况下,可以使用const关键字修饰变量,对变量做进一步的限制。
const是C语言的一个关键字,是所谓的类型限定符(Type Qualifiers)。表明一个变量不应该被明显地改变。
例如程序代码7-4中,如果希望用一个函数输出数组中不为0的数(那些素数),这个过程是不希望数组元素有任何改变的,这时可以把代码写成如下形式:
程序代码7-8

void shuchu(const int sz[],const int n)一句的具体解释如下。
■ const int sz[]表示的是,数组中的各个元素不可被显式地修改(const修饰的是int),比如被赋值,++、-等。而传进来的数组元素的个数n,尽管改变了对main()中没有什么影响,但可以确定的是在输出这个函数中是不变的,将其规定为const类别有一个额外的好处:就是一旦在函数内部误写了改变这个值的表达式,编译器通常会以编译错误或警告的形式向我们指出这一点。
■ const int n中的n这种变量,尽管不可以被修改(non-modifiable),但并不是常量,而是变量,并且是一个左值(5)。有的翻译称之为常变量(这让我想到“很黑的白色”这样让人忍俊不禁的修辞),也有的翻译称之为只读变量,因为这样的变量可能(不是一定)被某些编译器置放在只读的内存区域。后一种翻译可能比较靠谱,但远未臻完美。本书称呼这种变量为const变量。
const还可以用来实现构造复杂数据类型的“常量”,比如
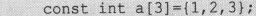
一旦能确定问题的初始数据是数组且在程序运行过程中保持数据不变化,这种定义是非常有用的,比起
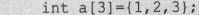
显然,前者安全。因为编译器可以帮助我们发现对数据无意中错误地修改。
const变量只可以在定义时被赋值,形参在本质上也是如此,因为形参在函数被调用时才拥有自己的存储空间。
const是说给编译器听的,没有这个类别修饰,对代码的功能并没有影响。但是一旦告诉编译器某个变量是const类别,那么编译器就有可能(不是一定)在编译时进行适当的优化,改善程序的功能。
7.4.6 例题——冒泡法排序
排序(Sort)是计算机科学的一个基本问题。几十年来,人们发明了数百种排序方法。
排序这个术语主要指由小到大排序,而所谓的由小到大是指非递减的性质。也就是说,只要不存在后面元素小于前面元素的情况,就称已排好顺序。
排序大体上可以分为3种方法:交换法、选择法、插入法。冒泡法排序属于交换法中的一种。它的排序过程是这样的
设有一组数据14、23、52、11
第1趟:
从前到后依次比较两个相邻元素的值,如果前面的大,则交换前后两个元素的值。因为有4个数据,所以要进行3次。
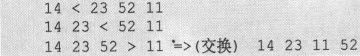
可以发现进行一趟这样的操作后,可以保证这组数据的最后一个是最大的。现在数据只剩前3个没有排好序。可以对前3个数据如法炮制。
第2趟:
因为只剩3个数据待排序,所以要进行2次。

第2趟结束后,可以发现数据的倒数第2个是数据中的次大者,换句话说,最后两个数据已经排好顺序且都在自己应该在的位置。现在只剩两个数据需要继续排序。
第3趟:

第3趟结束后,数据就已经排顺序了。由于这种方法不断地把较大的数据移动到后面,有些类似于水中的气泡向上冒的过程(越来越大),所以俗称冒泡法。
在一个main()函数中,针对一个特定的数组完成这样的操作可能并不是非常困难,要点是把握住每趟比较交换过程中数组下标的变化边界。但在学习了函数及结构化程序设计思想之后,那种把所有的事情都放在一个main()函数中完成的做法就显得极其业余甚至有些幼稚了。因此我们考虑一般的情形,并把这个工作交给一个函数来完成。
问题的提法:因为是对一个int类型的数组排序,所以解决问题的前提条件是知道数组名及数组元素的个数,也就是说函数应该有两个参数。函数的功能是对数组排序,结束后并没有什么特定的值要返回给调用函数的地方,所以函数的类型应该是void类型(当然如果你是喜欢汇报的人,你也可以把交换次数作为一个int返回),排序是它的一个副效应。如函数名取为paixu的话,它的函数原型应该是:
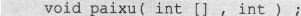
如果函数的形参分别为sz、ysgs,那么函数的头部,也就是对形参的声明应该是:

排序的过程是经过若干趟完成的,而每趟所做的事情都是比较交换若干次,这样就构成了一个循环。主要需要解决的问题是循环的次数。不难发现也不难证明,循环的次数为元素个数-1,即ysgs -1,显然这个写法第几趟是从1开始记数的。
每趟进行的工作都是若干次比较交换,因此这也是一个循环,这样就构成了一个循环嵌套。比较交换总是对于前后两个元素进行的,如果前面元素的下标用qian这个变量表示的话,那么后面元素的下标hou显然比qian大1。所有循环的一个重要问题是正确地确定循环次数,对于本问题来说也可以等价地说成是确定每趟qian或hou这两个变量的变化范围。这个变化范围显然与第几趟(djt)是有关的。通过对算法的观察与审视,不难发现qian总是从0开始到ysgs -1 -djt,这里djt是从1开始记数的。
如果djt从0开始记数,那么外层循环的循环条件显然是djt从0到ysgs-2,而每趟内层循环的下标qian是从0到ysgs-2-djt。
对于循环条件的分析是这种排序方法的重点和难点,因为稍有差池,不是造成越界访问的错误就是造成循环次数不够因而排序不充分的遗漏。下面是paixu()函数的代码。
程序代码7-9

要验证这段代码的正确性,还必须要有一个提供了原始数组的main()函数并编写一个输出数组各个元素的输出函数。提供原始数组的main()函数叫做驱动代码(用它来调用编写好的paixu()函数),而编写输出数组各个元素值的输出函数叫做“插桩”,因为没有它的支持,程序就无法完整地运行。请自己编写这两个函数以便测试paixu()函数的功能。然后再按照djt从0开始记数的方式重新编写一个paixu()函数。
7.4.7 测试与调试技巧——使用文件输入输出
在程序完成后,往往需要用多组数据进行测试以验证程序是否满足要求。而当输入或输出的数据较多时,通过改变数组的初值的方法来验证不但非常烦琐,而且每次修改数据都需要重新编译,这在有多套测试数据方案且每套数据都较多的时候,是令人无法忍受的。而通过调用scanf()函数,用手工的方式从键盘一一输入就更烦琐,且容易出错。
使用输入输出重定向可以把准备测试数据与程序的编辑、编译分离开来。
输入输出重定向有两种,一种是在操作系统层面上的输入输出重定向,如图7-4所示。
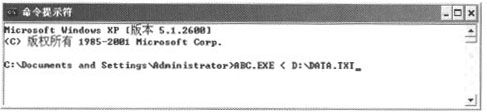
图7-4 在命令行重定向
图中表示的要运行的程序相应的可执行文件的名字为ABC.EXE。这个程序原本需要从键盘输入数据。但是<表示的是不再从键盘读取数据而转从D:\DATA.TXT(D:盘根目录下的DATA.TXT文件)这个文件读取数据。只要DATA.TXT中写的数据与在键盘上的输入一样,那么程序运行的效果和在键盘上输入是一样的。这个“<”就是输入重定向的意思。也可以使用输出重定向“>”把数据写到某个文件中而不显示在屏幕上。
这样只要在运行前把输入数据写在D:\DATA.TXT这个文件中就可以反复使用这个文件作为程序的输入了,这在调试程序和测试程序时都是十分方便的。
但是这种方法有一个不便的地方在于,必须退出编辑代码的编辑器(IDE),开启“命令提示符”才能实现。
仅仅通过程序代码也可以实现这种输入输出的重定向,这时不需要退出IDE进入“命令提示符”状态。下面一段代码就是实现从D盘根目录下的DATA.TXT文件输入一组数据并存储于数组之中的一个函数。
程序代码7-10

其中“freopen("D:\输入数据.txt","r",stdin);”表示的是把键盘(标准输入设备,stdin)的输入改为从数据文件“D:\输入数据.txt”中输入(注意,在C代码中,字符串字面量中的“\”表示一个“\”字符)。
“freopen("CON","r",stdin);”表示再把stdin重新定向回键盘(CON是Windows操作系统对键盘的一种文雅的表示尊重的正式称呼(6))。
在编程时只要把这段代码加入源代码中(不要忘记写函数原型),就可以用记事本在D盘根目录下编辑输入数据的文件了,编辑这个文件的原则是原来在键盘上怎么输入就怎么写。
当然,如果你不把准备的数据文件放在D盘根目录下,或者你更喜欢为数据文件取另外一个名字,你得适当修改代码中“D:\输入数据.txt”这个字符串内的内容。
freopen()函数也可以用来把输出结果重定向到磁盘文件中,方法是:

更详细的说明将在后面章节阐述,目前只要会用就可以了。
