8.2　C语言中复数类型的历史和现状

8.2.1　借助struct描述的复数类型

由于结构体是由若干个数据分量聚合成的一个完整的逻辑个体，而数学中的复数，恰恰是由实部和虚部两个部分组成，所以用结构体来描述数学中的复数是非常自然的。

当然，使用由两个数据元素构成的一维数组来描述复数也是一种可行的方案。但是由于复数中的实部和虚部之间并没有次序关系，所以这种数据描述方案显得不太自然，而且用0、1这样的下标来表示实部和虚部也很不直观（当然，这一点可以通过定义符号常量或枚举常量做些许改进）。

在早期，C语言定义复数类型使用类似下面的方式：

下面的代码是求两个复数乘积的示例。

程序代码8-6

运行结果：

由此我们可以看出，即使不增加新的语言成分，C89也可以很好地处理复数这样的数据对象。

8.2.2　_Complex、_Imaginary关键字（C99）

从前面小节中的示例可以看出，C语言并没有必要为复数这种类型增添新的语言成分。但是，出于为数值计算程序提供更好的支持的目的，C99还是增加了Complex、_Imaginary这两个关键字。这两个关键字和_Bool一样，看起来就很怪异、很不C。它们都以“”（下划线）开头，并且第一个字母是大写。这主要是为了避免和现存的一些已经使用bool、complex和imaginary这样标识符的C代码冲突。这样，以下划线开头、第一个字母大写似乎就成了一种命名标识符时潜在的、无形的禁忌，毕竟这样多些风险。

_Complex、_Imaginary这两个关键字和struct、enum、union等关键字一样，并不是完整的具有类型名称意义的关键字，只能算做半个类型名字，要成为完整意义的类型名字必须与其他单词组合。对于这两个关键字来说，下面是它们所能构成的类型的名字。

其中，次序不是必须遵守的，比如float _Complex也可以写成_Complex float。

有了类型的名字就可以定义这种类型的变量了。如

由于同样需要两个部分构成类型的名字，从简洁性方面看，double _Complex与前小节中的struct fushu相比并没有什么特别的优势。但不同之处在于，使用double _Complex定义变量时，初始化可以更加直观。如

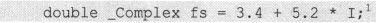
¹ Dev C＋＋中的写法和C99标准的规定有些小差异，Dev C＋＋中写复数类型常量时不需要那个“*”。

这种新的复数类型的另外一个很强的优势在于，它被归为了算术类型（Arithmetic Types），因此可以直接作为“＋”、“－”、“*”、“/”运算符的操作数，这是struct fushu类型所望尘莫及的。同样以前一小节中的问题为例，代码可以写成：

程序代码8-7

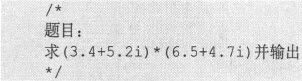
运行结果：

其中creal()、cimag()分别为求double _Complex类型量的实部和虚部的两个库函数。类似地，carg()、cabs()可以求出double _Complex类型量的辐角和模。要使用这些函数，需要在代码中声明这些函数的函数原型，这可以通过编译预处理命令#include <complex.h>实现，而且一旦如此，就可以用complex替代_Complex这个显得有些丑陋的关键字。

在complex.h中还给出了不少其他复数计算的库函数的函数原型，如

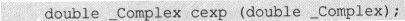
可以计算自然常数e的附属次幂。下面的示意性代码用著名的欧拉公式⁽²⁾验证了cexp()的计算能力。

程序代码8-8

运行结果：

尽管C99增加了_Complex、_Imaginary这两个关键字，但却没有硬性规定编译器必须支持这两个关键字，尤其是_Imaginary，在任何环境下都不是必须支持的，而_Complex关键字对于独立式环境（Freestanding Environment，没有操作系统支持，C程序独立运行的情况下）是可以不支持的。目前支持这两个关键字的编译器并不多见。