6.10　递归

6.10.1　什么是递归

递归（Recursion）是现实世界中普遍存在的一种现象，这种现象的特点就是某个过程以某种方式不断地重复出现。

用两面镜子互相照，很容易发现镜子的镜像中还有镜子的镜像，镜子的镜像中的镜子的镜像中还有镜子的镜像……

植物的生长也是如此，植物长出一片叶子或花瓣后，过段时间在另一个地方又长出另一片叶子或花瓣。

庄子的“一尺之捶，日取其半，万世不竭。”描述的是一个反复进行的过程（日取其半），这也是一种递归。

由此可见，递归在本质上是一种重复或循环，这种重复或循环有时是以简单的方式进行的，而有时是以比较复杂的方式进行的。

在人类的思维领域也存在大量递归的例子，比如数学中阶乘的定义就是用递归的方式描述的（用阶乘本身对阶乘进行定义）：

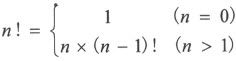
数学归纳法的思想也和递归有异曲同工之妙。用数学归纳法证明对一切自然数n都成立的命题一般步骤是：①证明这个命题对自然数1成立；②假设当n取某一自然数k时命题正确，以此推出当n=k+1时这个命题也正确。有了①、②就可以断言命题对所有的自然数n都成立了。

数学归纳法的这种思考方法通常叫做递推。递推成立的前提有两个，首先需要有个递推的基础（n=1时命题成立），其次是建立递推的关系（若n=k时成立则n=k+1时成立）。

反过来，当求解一个关于自然数n的问题时，如果可以把问题简化成关于n－1的问题，而且对于n=1这个问题可以解决的话，那么这个问题就解决了。这种思维方式就叫做递归。

递归同样需要有个递归的关系，这个依据就是把问题简化（把对n求解的问题变成对n－1的问题），此外递归还需要有递归的终止（对于1问题可解）。

例如，当需要求f(n)=1+2+3+……+n的值时，由于这个问题可以简化成n+f(n－1)，而且当n为1时问题的答案f(1)明显为1，这样的问题就可以视为已经解决了。而具体的求解方法则可以由n=1时的解答f(1)得到n=2时问题的解答(f(2)=2+f(1)=3)，再由f(2)可以求得f(3)=3+f(2)=6……只要n为有限值，总能得到最终所要求的解答。如果把问题不断简化的过程（把对n的问题简化成对n－1的问题的过程）理解为“递”的话，那么从“递”的终止点(f(1)=1)开始，求f(2)，再由f(2)求得f(3)……直到求得f(n)这个过程就是“归”。“递”的终点就是“归”的起点。

因此，递归也是人类的一种思维方式，同样递归有时也是描述解决问题的方法的一种方式。当解决问题的方法可以用递归的方式来描述时，在程序中使用递归技术来解决问题也就顺理成章了。

6.10.2　递归是函数对自身的调用

使用递归的前提是具备递归的思想，即用递归的方法思考解决问题的方法和步骤，而程序则是对这种方法和步骤的自然描述。在程序实现上，递归就是函数通过对自身的调用来描述自己的函数定义。

很多人都听过这样的故事：

“从前有个山，山里有个庙，庙里有个老和尚给小和尚讲故事。讲的什么呢？”

“从前有个山，山里有个庙，庙里有个老和尚给小和尚讲故事。讲的什么呢？”

“从前有个山，山里有个庙，庙里有个老和尚给小和尚讲故事。讲的什么呢？”

……

这是个明显的递归例子。在每次讲到“讲的什么呢？”之后，又开始讲故事，而讲的故事恰恰是刚刚讲过的内容。如果把讲故事的过程抽象为一个函数，那么在函数完成“讲的什么呢？”之后的行为，就完全可以用对自身的调用来实现。下面是揭示这一过程的示意性伪代码。

这个过程会无限度地进行下去，这叫无限递归。在程序中不允许一个无限进行的过程（算法必须经有限步骤完成），就如同程序不允许死循环一样。

在程序中，使用递归的函数必须在一定条件下使递归终止。“讲故事”函数的一个比较现实可行的版本应该是：

新版本的“讲故事”函数将把需要讲故事的次数作为参数，讲完之后再继续调用自身，而是返回到程序最初调用“讲故事”函数的地方继续执行。

6.10.3　递归的实现过程

下面以一个极简单的例子说明递归过程是如何实现的。

程序的运行结果为：

如图6-2所示，描述了递归调用过程程序的执行轨迹（“递”的过程写“归”的过程，英语单词recursion不求“信达雅”的字面翻译应该是“来回”（re-）“跑”（cur）的意思，必须承认的是“递归”这个翻译比“来回跑”这个翻译“雅”多了，虽然也难理解多了），这个过程与用递归的思想求f(n)=1+2+3+……n的值的过程是极其类似的。

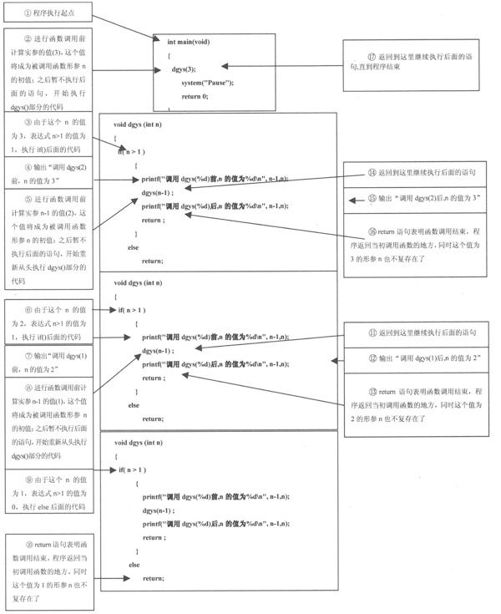
图6-2　递归执行过程

从图中还可以发现对dgys()函数的每次调用，dgys()函数都有自己的一个“私有”的形参n，这个形参一直被保留到本次调用结束才消失，而在函数调用结束前则一直被保留着。对于函数本地的局部变量也是如此（除非是static存储类别的局部变量），每次调用时局部非static变量也都有自己的“私有”副本。⁽¹⁴⁾

此外需要说明的是，为了演示的方便，前面源程序中dgys()部分的代码有些不够简洁，更为简洁的写法如下，请读者参考前面的示意图自己练习着分析一下执行过程。

6.10.4　递归与循环

从递归调用过程程序的执行轨迹中还可以看出，递归本质上可以看作是以形参为“循环变量”的、对函数调用的“循环”。这种循环和普通的变量循环（有时也被叫做迭代）不同的是它是双向的，除了有一个“去”的过程（“递”）还有一个回的过程（“归”）。因此一切可以用循环实现的算法也都可以用递归实现，反过来也是如此。

以前面提到的求f(n)=1+2+3+……n值问题为例，下面的程序代码通过两种方式求解。

这个程序中，假设输入5，xhqiuhe()函数使用了两个变量进行计算，而dgqiuhe()函数由于还需要调用dgqiuhe(4)、dgqiuhe(3)、dgqiuhe(2)、dgqiuhe(1)才能完成dgqiuhe(5)的计算，而每次调用至少需要一个自身私有的n，所以至少需要5个变量的内存开销（此外还有记录执行位置的内存开销和运算时间上的开销）。所以一般来讲，递归的方法比循环的方法在内存和运算时间上的开销要大。此外，过多的递归会导致溢出。因此，递归从来不是无限度的，各个编译器都对递归的深度有所限制。

递归的优点在于对递归思想的有力表达和体现。递归在表达形式上非常简洁，所表达的思想不容置疑，在表达思想的贴切和自然方面是无与伦比的。因此用递归写成的代码往往给人一种优雅且从容不迫的优美感觉（代价是牺牲内存和速度）。

练习

1．编写递归函数，求1+3+5+……+(2n+1)。自己编写程序验证函数的功能是否能正确实现。

2．编写递归函数，求两个正整数的最大公约数。自己编写程序验证函数的功能是否能正确实现。

3．编写递归函数，求一个大于2的正整数的所有质因子之和。

6.10.5　递归的力量——Hanoi塔问题

Hanoi塔问题是一个古老的智力游戏。这个游戏需要3根柱子（如图6-3所示）和若干大小不等的空心圆盘。一开始，所有的圆盘依由大到小的顺序插放在第一根柱子上。游戏者必须依照下面两条规则把所有的圆盘移动到第3根柱子上。

图6-3　Hanoi塔

（1）每次只能拿取某根柱子上最上面的一个圆盘。

（2）取出的圆盘必须马上插放到另一根柱子上，且必须保证较大的圆盘不被放在较的小圆盘上面。

在盘子不太多的情况下，相信一般的读者都可以按照规则凭借直觉顺利地完成这个任务。但让计算机完成这个任务则是另一回事。因为计算机没有直觉，我们也不可能告诉计算机我们的直觉。让计算机完成任务就必须告诉计算机完成任务的方法和步骤。

可以用循环的方式解决这个问题，但这个算法不但需要使用较为复杂的数据来描述，且其本身也难以理解、过程复杂且不易表述。让我们体验一下递归的力量和优美。

首先，必须要确定的一件事情是问题是否可解。如果问题无解也就根本没有编程解决问题的必要了。为了解决这个问题，先从简单的情形开始推理。

（1）在只有1个圆盘的情形下，它可以不违背规则地从第1根柱子移动到第3根柱子。这点用不着更多的解释。

（2）同理，在只有1个圆盘的情形下，它同样可以不违背规则地从第1根柱子移动到第2根柱子。

（3）在有2个圆盘的情形下，由于（1），所以可以先把第1个圆盘从第1根柱子移动到第2根柱子（较大的第2个圆盘在这个过程中没有移动，所以不会产生违背规则的问题），再把第2个圆盘不违背规则地移动到第3根柱子上（第3根柱子目前是空着的），最后再把第2根柱子上的圆盘移动到第3根柱子上（较大的第2个圆盘在这个过程中也没有移动，所以也不会产生违背规则的问题）。结论是可以不违背规则地把2个圆盘从第1根柱子移动到第3根柱子上。

（4）同理，在有2个圆盘的情形下，可以把这2个圆盘在遵守规则的前提下从第1根柱子移动到第2根柱子上（相对第1根柱子，第2根和第3根柱子在地位上完全是对称对等的，可以移动到第3根柱子上当然可以第2根柱子上）。

（5）类似地，由于（1）可以推论出能够不违背规则地把3个圆盘不违背规则地从第1根柱子移动到第3根柱子上的结论。

（6）由于（1），且由于相对第1根柱子，第2根和第3根柱子在地位上完全是对称对等的，所以可以推论出能够不违背规则地把3个圆盘不违背规则地从第1根柱子移动到第2根柱子上的结论。

（7）……

至此，通过递推的办法可以确定问题可解。顺理成章地，还可以从上面的推理中得到解决问题的策略和步骤如下。

对于n个圆盘，

（1）首先从第1根柱子移动n－1个圆盘到第2根柱子上。

（2）把第1根柱子剩的最后一个圆盘移动到第3根柱子上。

（3）把第2根柱子上的n－1个圆盘移动到第3根柱子上。

用移动n－1个圆盘来描述移动n个圆盘的解决方案，且1个圆盘的移动方法已知，这个解决方案明显是递归性质的，用函数的递归来实现是非常自然的。

从这个程序代码中可以看到，对于如此复杂的问题，递归的代码居然可以写得异常简洁却同时又把解决问题的思想表达得恰倒好处且淋漓尽致，这就是递归的魅力之所在。

写递归代码的前提是具备递归的思想，递归思想的本质是把问题简化，最终简化至问题可以解决。这种思维方式需要通过不断的自我训练才能建立并完善。

在代码中，递归体现为函数定义中用函数的自我调用来描述。由于程序中的递归必须是有穷递归，所以递归函数总是由递归的过程（问题的不断简化）及递归的终止（问题简化到可以解决的程度）两个部分组成的，这使得递归函数在形式上几乎总是使用if语句来实现⁽¹⁵⁾，而且在递归函数中往往可能需要不止一个return语句。在这方面初学者容易犯的一个错误是，忘记写其中某个必需的return语句，或者由于忘记递归的终止或由于不正确的递归过程导致无限递归。

练习

1．自己独立完成Hanoi塔问题的程序。

2．题目：有1、2、3、4个数字，能组成多少个互不相同且无重复数字的三位数？都是多少？

3．输入一正整数，输出等于这个数的所有可能的由小到大的若干正整数相加的式子。例如对于7：

6.10.6　间接递归

除了函数直接调用自身的情形外，还有一种在函数定义时需要调用其他函数，而其他函数的定义又反过来需要调用前一个函数的情形，这种情形叫间接递归。

假定银行一年整存零取的月息是0.63％。现在某人打算存入银行一笔钱，然后在每年年底取出1000元，在第5年年底刚好取完，请问他该存入多少钱（精确到厘）。

分析：问题相当于第1年到第5年每年年初都存一次钱，数额是每年年底的本息÷（1+12×0.63％），而前4年年底的本息都是下一年年初存钱数额+1000，第5年年底的本息是1000。

运行结果：第1年需存钱：4039.444元

练习

兔子繁殖问题：一对小兔，出生一个月后变成大兔子，两个月后生出一对小兔子，自己变成老兔子，上个月的小兔子变成大兔子，按此规律并假设兔子没有死亡，计算n个月后共有多少只兔子。