7.3　熟练应用一维数组

7.3.1　一维数组的遍历

对数组最为常见的操作是对数组元素的遍历（Traversal，通俗地说就是把数组中每个元素都访问一次，或者更通俗地说就是逐个地读或写一次），下面的代码演示了对bjs数组中各个元素依次写入再依次读出之后输出。

程序代码7-2

程序运行结果：

注意在前面的for语句中，下标变量i总是从0开始，而中间的循环条件部分为“i<数组元素的个数”，这样在循环变量每次加1的情况下，循环的次数一定等于“数组元素个数”。为了保证循环次数的正确性，应该把这个句式作为固定的句型来学习以养成自己的编程习惯，这样就不至于在写代码时每次都考虑循环次数的问题了，从而可以把精力用在思考更重要的问题上。

7.3.2　翻卡片问题

例题：54张卡片，依次排成一列，初始状态皆为正面向上。第一遍，把各张卡片各翻一次使之反面朝上，第二遍把第2、4……54张卡片各翻一次，第三遍把第3、6……54张卡片各翻一次……最后一遍把第54张卡片翻一次，问最后哪些卡片正面向上哪些反面向上。

问题分析：每张卡片有两种状态，可以分别用两个整数0和1表示，这样翻的动作可以简单地用！运算实现。因为一共有54张卡片，所以可以用一个由54个int整数构成的一维数组来表示这54张卡片。翻卡片一共54遍。

程序代码7-3

练习

旅馆里有100个房间，从1到100编了号。第一个服务员把所有的房间门都打开了，第二个服务员把所有编号是2的倍数的房间“相反处理”，第三个服务员把所有编号是3的倍数的房间作“相反处理”，……，以后每个服务员都是如此。问第100个服务员来过后，哪几扇门是打开的（所谓“相反处理”是：原来开着的门关上，原来关上的门打开）。

7.3.3　筛法

例题：编程求出100以内的所有素数。

古希腊数学家埃拉托色尼（Eratosthenes）建立了素数的概念并提出了一种求素数的方法——筛法，这种方法可以给出某个自然数之内的所有素数。假设要求30以内的所有素数，首先依序写出1到30之内的所有自然数

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

由于1不是素数，把1划掉

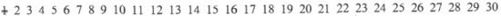
然后从前向后找到的第一个数2就是素数。再把2的倍数都划掉（自身不划）

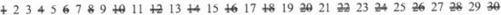
再从2继续往后找，遇到的第一个没被划掉的数3也是素数。再把3的倍数划掉

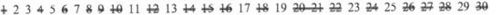
再从3继续往后找，遇到的第一个没被划掉的数是5，再把5的倍数划掉

……

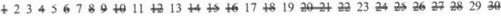
一直依据这样的原则，遇到一个没被划去数的就划去它的倍数，遇到被划去的就继续看下一个数，直到最后。

下面代码中以值为0（BSSS）表示不是素数，用筛法求出100以内的素数。

程序代码7-4

代码中，第二个循环语句for(i = 0；1<GS；i＋＋)的i明显不需要循环到GS-1，事实上一般只要到GS/2甚至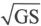就够了。这是前面代码在效率方面需要改进的地方。

第二个循环语句循环体内的if语句，也可以写成：

程序代码7-5（片段）

这和前面的代码是等效的，但看起来更简洁些。

7.3.4　一维数组元素的赋初值

和基本类型变量可以在定义时赋初值一样，数组也可以在定义时给各元素赋初值或给部分数组元素赋初值。

不同之处在于，给数组赋值通常需要一组数据，数据之间要用“,”隔开，而且这组数据需要用“｛｝”括起来。

下面以实例说明：

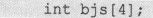
这样定义的数组bjs的各元素都是没有意义的“垃圾值”。

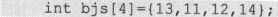
这样定义的数组bjs的各元素bjs[0]、bjs[1]、bjs[2]、bjs[3]值依次为：13、11、12、14。

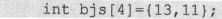
这样定义的数组bjs的元素bjs[0]、bjs[1]的值依次为：13、11，其余的各元素皆为0。

不提倡的方法（但合法）：

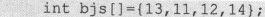
数组共4个元素，bjs[0]、bjs[1]、bjs[2]、bjs[3]的值依次为：13、11、12、14。

最后一种方法不被提倡的原因是，数组元素的个数有时很容易搞错，且不容易检查。数组元素的个数还是明确写出为好。

注意，这种赋初值的方法只可用于定义数组的时候，除此之外，数组不可以被整体性地赋值。

C99对数组赋初值的方法做了增补，允许为特定下标的数组元素指定初值，如：

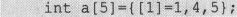
这样定义的数组a的元素a[1]、a[2]、a[3]的值依次为：1、4、5，其余的各元素皆为0。

也可以对同一个元素指定初值多次，最后一次有效。

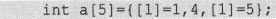
但这样做通常并没有多少实用价值。