6.3　函数

大多数的变量类型仅用于存储数据，而函数能够让我们和数据一起工作，它们是“动词”而非“名词”。和环境类似，它们是另一种我们可以分配、操纵，甚至将它传递给其他函数的数据类型。

6.3.1　创建和调用函数

为了更好地了解函数，我们来看看它的组成。

键入一个函数的名称，将显示其运行的代码。以下是rt函数，该函数将生成基于T分布的随机数1：

1 如果定义是类似于UseMethod（"my_function"）或standardGeneric（"my_function"）的一行内容，请参阅16.7节。如果R抱怨找不到对象，尝试getAnywhere（my_function）。 

  1. ## function (n, df, ncp) 
  2. ## { 
  3. ## if (missing(ncp)) 
  4. ## .External(C_rt, n, df) 
  5. ## else rnorm(n, ncp)/sqrt(rchisq(n, df)/df) 
  6. ## } 
  7. ## <bytecode: 0x0000000019738e10> 
  8. ## <environment: namespace:stats>

如你所见，rt需要三个输入参数：n是要产生的随机数的数目、df是自由度值、ncp是一个可选的非中心参数。从技术上来说，这三个参数n、df和ncp是rt函数的形式参数（formal argument）。当你调用该函数并给它传递值时，这些值被称为参数。

注意

参数和形式参数之间的差异不是很重要，因此接下来本书没有区分这两个概念。

在大括号之间，你可以看到函数体内代码行。它们就是每次调用rt时要执行的代码。

请注意，这里有没有显式的“return”关键字声明应该从函数返回哪个值。在R中，函数中计算的最后一个值将自动返回。以rt为例，如果ncp参数被省略，将会调用C代码生成随机数并返回。否则，该函数会调用rnorm、rchisq和sqrt函数计算并返回值。

要创建我们自己的函数，只需像其他任何变量一样为它赋值。举一个例子，创建一个函数来计算直角三角形斜边的长度（为简单起见，我们将使用一般的算法。但不要在实际项目中使用这些代码，因为它们在数字很大或很小时并不适用）：

  1. hypotenuse <- function(x, y) { 
  2.     sqrt(x ^ 2 + y ^ 2) 
  3. }

这里，hypotenuse是我们正在创建的函数，x和y是它的参数（形参），在大括号中的内容是函数体。

事实上，因为函数体只有一行代码，可省略大括号：

  1. hypotenuse <- function(x, y) sqrt(x ^ 2 + y ^ 2)  # 和之前一样

注意

R对于代码如何使用空白符很宽容，所以“一行代码”可以延伸到多行。没有使用大括号的大量代码也是一条语句（statement）。语句的确切定义涉及技术术语，但从实用角度看，它就是在执行前你可在命令行中键入的代码量。

现在，我们可以使用以下任意一种方式来调用这个函数：

  1. hypotenuse(3, 4)
  3. ## [1] 5
  5. hypotenuse(y = 24, x = 7)
  7. ## [1] 25

当我们调用函数时，如果不命名参数，则R将按位置匹配它们。以hypotenuse(3, 4)为例：3是第一个参数，因此它对应x；4是第二个参数，因此它对应y。

如果要改变我们传递参数的顺序，或省略其中一些，则可传入命名参数。以hypotenuse(y = 24, x = 7)为例，虽然传递变量的顺序是“错误”的，但R仍能正确地判断出哪个变量应被映射到x、哪个变量应被映射到y。

它对于计算斜边的函数来说意义不大，但如有需要，我们可以给x和y提供默认值。在以下新版本的代码中，如果我们不给函数传递任何值，则x会取默认值5而y会取12：

  1. hypotenuse <- function(x = 5, y = 12) 
  2. { 
  3.     sqrt(x ^ 2 + y ^ 2) 
  4. } 
  5. hypotenuse()     # 与hypotenuse(5, 12)相等
  7. ## [1] 13

我们已经见到过formals函数，它能取得函数的参数并返回一个（结对）列表。args函数也能做相同的事，看上去更加可读但编程风格不太友好。formalArgs函数将返回参数名称的字符向量：

  1. formals(hypotenuse)
  3. ## $x 
  4. ## [1] 5
  5. ## 
  6. ## $y 
  7. ## [1] 12
  9. args(hypotenuse)
  11. ## function (x = 5, y = 12) 
  12. ## NULL
  14. formalArgs(hypotenuse)
  16. ## [1] "x" "y"

body函数可用于返回函数体。单独地，它不太有用。但有时我们需要以文本的方式检查它们，例如要查找一个调用了另一函数的函数。对此，我们可以使用deparse函数：

  1. (body_of_hypotenuse <- body(hypotenuse))
  3. ## { 
  4. ## sqrt(x^2 + y^2) 
  5. ## }
  7. deparse(body_of_hypotenuse)
  9. ## [1] "{" " sqrt(x^2 + y^2)" "}"

函数形参的默认值不仅仅是常数值，我们还可以把任何R代码放进去，甚至使用其他形参。下面的normalize函数将缩放一个向量。默认情况下，参数m和s是第一个参数的平均值和标准差，所以返回的向量将包含均值0和标准差1：

  1. normalize <- function(x, m = mean(x), s = sd(x)) 
  2. { 
  3. (x - m) / s 
  4. } 
  5. normalized <- normalize(c(1, 3, 6, 10, 15)) 
  6. mean(normalized)     #几乎是0!
  8. ## [1] -5.573e-18
  10. sd(normalized)
  12. ## [1] 1

不过，normalize函数有一个小问题，如果x的某些元素没有给出，我们将看到：

  1. normalize(c(1, 3, 6, 10, NA))
  3. ## [1] NA NA NA NA NA

如果向量的所有元素都没有给出，那么在默认情况下mean和sd都将返回NA。因此，normalize函数的返回值中的所有元素都是NA值。如果有这样的选项：只有输入值是NA时才返回NA，那可能更好。mean和sd都有一个参数na.rm，它能让我们删除计算之前的任何缺失值。为了避免所有的NA值，我们可以在normalize中包含这个参数：

  1. normalize <- function(x, m = mean(x, na.rm=na.rm), 
  2.     s=sd(x, na.rm=na.rm), na.rm=FALSE) 
  3. { 
  4.     (x - m) / s 
  5. } 
  6. normalize(c(1, 3, 6, 10, NA))
  8. ## [1] NA NA NA NA NA
  10. normalize(c(1, 3, 6, 10, NA), na.rm=TRUE)
  12. ## [1] -1.0215 -0.5108 0.2554 1.2769 NA

此方法可行，但语法有点笨拙。为了避免输入那些实际上没有被函数用到的参数名（na.rm只被传递到mean和sd中），R提供了一个特殊参数…，它包含了所有不能被位置或名称匹配的参数：

  1. normalize<-function(x, m=mean(x, ...), s=sd(x, ...), ...) 
  2. {
  3.     (x-m)/s 
  4. } 
  5. normalize(c(1, 3, 6, 10, NA))
  6. ## [1] NA NA NA NA NA
  8. normalize(c(1, 3, 6, 10, NA), na.rm=TRUE)
  9. ## [1] -1.0215 -0.5108 0.2554 1.2769 NA

现在，在normalize(c(1, 3, 6, 10, NA), na.rm=TRUE)的调用里，参数na.rm并不能匹配normalize的任何形参，因为它不是x、m或s。这意味着它被存储在normalize的参数…里。当我们评估m时，表达式mean(x, …)现在为mean(x, na.rm=TRUE)。

如果你对此还不太清楚，不用担心。大多数时候，它的工作原理是一个我们无需操心的高级话题。当下，你只需了解…能将参数传递给子函数。

6.3.2　向其他函数传递和接收函数

函数可以像其他变量类型一样地使用，我们可将之作为其他函数的参数，并且从函数中返回。一个常见的，把其他函数当成参数的例子是do.call。此函数提供了一种调用其他函数的替代语法，让我们可以像列表一样传递参数而非逐次传递：

  1. do.call(hypotenuse, list(x = 3, y = 4))     # 和hypotenuse(3, 4)一样
  3. ## [1] 5

也许最常见的案例为do.call与rbind混用。结合这两个函数，你可以一次拼接多个数据框或矩阵：

  1. dfr1 <- data.frame(x = 1:5, y = rt(5, 1)) 
  2. dfr2 <- data.frame(x = 6:10, y = rf(5, 1, 1)) 
  3. dfr3 <- data.frame(x = 11:15, y = rbeta(5, 1, 1)) 
  4. do.call(rbind, list(dfr1, dfr2, dfr3))     # 和rbind(dfr1, dfr2, dfr3)一样
  7. ##     x        y
  8. ## 1   1  1.10440
  9. ## 2   2  0.87931
  10. ## 3   3 -1.18288
  11. ## 4   4 -1.04847
  12. ## 5   5  0.90335
  13. ## 6   6  0.27186
  14. ## 7   7  2.49953
  15. ## 8   8  0.89534
  16. ## 9   9  4.21537
  17. ## 10 10  0.07751
  18. ## 11 11  0.31153
  19. ## 12 12  0.29114
  20. ## 13 13  0.01079
  21. ## 14 14  0.97188
  22. ## 15 15  0.53498

花一些时间去习惯这种用法是值得的。在第9章中，我们将大量地使用apply及其衍生函数把函数传递到其他函数中。

把函数用作参数时，没必要一开始就为它们赋值。以同样的方式将以下函数：

  1. menage <- c(1, 0, 0, 1, 2, 13, 80) #参考http://oeis.org/A000179 
  2. mean(menage)
  3. ## [1] 13.86

简化为:

  1. mean(c(1, 0, 0, 1, 2, 13, 80))
  2. ## [1] 13.86

我们还可以以匿名方式传递函数:

  1. x_plus_y <- function(x, y) 
  2. x + y 
  3. do.call(x_plus_y, list(1:5, 5:1))
  4. ## [1] 6 6 6 6 6
  6. # 与下相同 
  7. do.call(function(x, y) x + y, list(1:5, 5:1))
  8. ## [1] 6 6 6 6 6

返回值为函数的情况比较罕见，但它是有效的。ecdf函数将返回一个向量的经验累积分布函数，如图6-1所示。

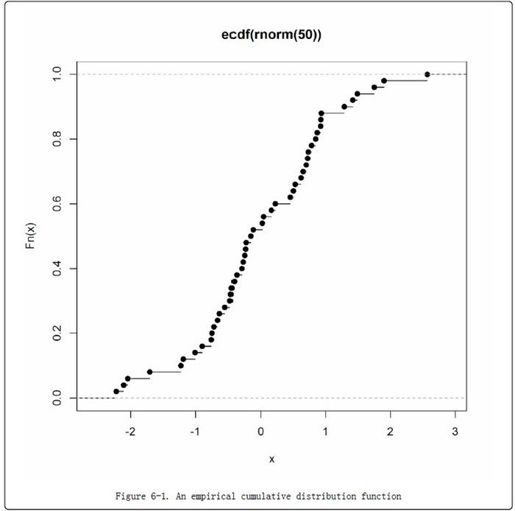6-1 经验累积分布函数 图6-1：经验累积分布函数

  1. (emp_cum_dist_fn <- ecdf(rnorm(50)))
  3. ## Empirical CDF 
  4. ## Call: ecdf(rnorm(50)) 
  5. ## x[1:50] = -2.2, -2.1, -2, ..., 1.9, 2.6
  7. is.function(emp_cum_dist_fn)
  9. ## [1] TRUE
  11. plot(emp_cum_dist_fn)

6.3.3　变量的作用域

变量的作用域是指你在哪里可以看到此变量。例如，当你在函数内部定义一个变量时，该函数中下面的语句将能访问到该变量。在R（但不是S）中，子函数也能访问到这个变量。在下例中，函数f的参数为x，且它将被传递给函数g。f还定义了一个变量y，它的作用域在函数g的范围内，这是由于g是f的子函数。因此，即使没有在g里定义y，下例也能工作：

  1. f <- function(x) 
  2. { 
  3.     y <- 1 
  4.     g <- function(x) 
  5.     { 
  6.         (x + y) / 2     #y被使用了，但它不是g的形式参数 
  7.     } 
  8.     g(x) 
  9. } 
  10. f(sqrt(5))     # 这也能工作！它神奇地在环境f里找到了y
  12. ## [1] 1.618

如果我们修改例子，把g定义在f以外，使g不是f的子函数，那么例子将抛出一个错误，因为R找不到y：

  1. f <- function(x) 
  2. { 
  3.     y <- 1 
  4.     g(x) 
  5. } 
  6. g <- function(x)
  7. { 
  8.     (x + y) / 2 
  9. } 
  10. f(sqrt(5))
  12. ## January February March April May 
  13. ## 0.6494 1.4838 0.9665 0.4527 0.7752

在6.2节中，get和exists函数在其父环境和当前环境下搜索变量。变量作用域的工作方式与此完全相同：R将试图在当前的环境变量下寻找变量，如果找不到则会继续在父环境中搜索，然后再在该环境的父环境中搜索，以此类推，直到达到全局环境。在全局环境中定义的变量在任何地方都可见，这就是它们被称为全局变量的原因。

在第一个例子中，f的环境是g的父环境，因此y能被发现。在第二个例子中，g的父环境是全局环境，它不包含变量y，所以它会抛出一个错误。

变量可在父环境中被发现，这种作用域系统通常很有用。但它也会带来有缺陷、糟糕和难以维护的代码。考虑下面的函数h：

  1. h <- function(x) 
  2. { 
  3.     x * y 
  4. }

这看起来不能工作，因为它只接受一个参数x，但它的函数体中却使用了两个参数x和y。我们在干净的用户工作区试试：

  1. h(9)
  2. ## January February March April May 
  3. ## -8.436 6.583 -2.727 -11.976 -6.171

到目前为止，我们的直觉是正确的。y没有被定义，所以该函数将抛出一个错误。现在来看看，如果把y定义在用户工作区，会发生什么：

  1. y <- 16 
  2. h(9)
  3. ## [1] 144

当R在h的环境中无法找到一个名为y的变量时，它会在h的父环境，即定义了y的用户工作区（即全局环境）中搜索，然后就能得出正确的乘积。

应谨慎地使用全局变量，因为它很容易引出错得离谱的代码。在以下被修改过的函数中，h2 和y将有一半的几率被随机定义为局部变量。因为y被定义于用户工作区中，所以当它执行时y是局部变量还是全局变量完全是随机的！

  1. h2 <- function(x) 
  2. { 
  3.     if(runif(1) > 0.5) y <- 12 
  4.     x * y 
  5. }

我们使用replicate运行几次来查看其结果：

  1. replicate(10, h2(9))
  2. ## [1] 144 144 144 108 144 108 108 144 108 108

如果用runif函数产生的均匀分布的随机数（在0和1之间）比0.5大时，局部变量y被赋值为12。否则，将使用全局值16。

我敢肯定你已经注意到，这非常容易使代码隐藏有错误。通常来说，更好的做法是显式地向函数传递我们需要的所有变量。