2.6 表示概率质量函数

Pmf.py中定义了用于表示概率质量函数的Pmf类。这里稍微解释一下：Pmf是模块的名称，也是类的名称，因此这个类的全称是Pmf.Pmf。pmf则通常被我用做变量名。在正文中，我用PMF指代通常意义上的概率质量函数，这个简写与我的实现无关。

用MakePmfFromList方法创建Pmf对象，其参数是一组值：

  1. >>> import Pmf
  2. >>> pmf = Pmf.MakePmfFromList([1, 2, 2, 3, 5]) 
  3. >>> print pmf
  4. <Pmf.Pmf object at 0xb76cf68c>

Pmf对象跟Hist对象有很多类似的地方，两者的Values方法和Items方法是一样的。最大区别在于Hist是将值映射到一个用整数表示的数量，而Pmf是将值映射到一个用浮点数表示的概率。

用Prob查看给定值的概率：

  1. >>> pmf.Prob(2) 
  2. 0.4

可以通过增加某个值的概率来修改现有的Pmf：

  1. >>> pmf.Incr(2, 0.2) 
  2. >>> pmf.Prob(2) 
  3. 0.6

还可以将概率扩大若干倍：

  1. >>> pmf.Mult(2, 0.5) 
  2. >>> pmf.Prob(2) 
  3. 0.3

如果修改Pmf，有可能导致整个PMF不再是归一化的，也就是说所有概率的总和不再等于1。可以用Total方法检查一下，该方法会返回所有概率的总和：

  1. >>> pmf.Total() 
  2. 0.9

要重新归一化，调用Normalize：

  1. >>> pmf.Normalize() 
  2. >>> pmf.Total()
  3. 1.0

Pmf对象提供的Copy方法可以复制Pmf对象，修改复制出来的Pmf对象不会影响原来的数据。

习题2-4

根据维基百科：“生存分析是统计学的一个分支，涉及生物体的死亡和机械系统故障。”详见http://wikipedia.org/wiki/Survival_analysis。

作为生存分析的一部分，计算剩余使用寿命（例如某个机械部件还能用多长时间）是大有用处的。如果知道使用寿命的分布和部件的使用时间，就可以计算出剩余使用寿命的分布。

编写一个函数RemainingLifetime，参数是表示使用寿命的Pmf对象和使用时间，返回一个表示剩余使用寿命分布的Pmf对象。

习题2-5

2.1节介绍过，通过累加各个元素并除以ｎ可以算出样本的均值。对于给定的PMF，也可以算出均值，但计算过程略有不同：

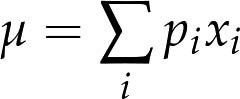
2.6 表示概率质量函数 - 图1

其中xi是PMF中的值，pi=PMF(xi)。同样，也可以计算方差：

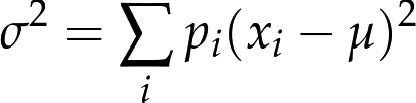
2.6 表示概率质量函数 - 图2

编写两个函数，PmfMean和PmfVar，两者的参数都是一个Pmf对象，分别计算它的均值和方差。看一看结果是否跟Pmf.py中的Mean和Var方法的结果一致。